АВТОМАТИЗАЦИЯ ПРОВЕРКИ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАНИЙ

Приводится обзор систем автоматической и автоматизированной проверки решений инженерно-графических заданий. Исследуются вопросы автоматизации проверки. Приводятся результаты разработки системы автоматической проверки решений в формате DXF и внедрения ее в состав интернет-системы.

Введение

В предыдущем докладе [1] было дано определение верификации и выделены группы задач верификации инженерно-графических заданий, было показано применение геометро-графических тренажеров для проверки элементарных навыков проекционного моделирования (первая группа задач верификации). Значительно больший интерес представляют другая группа — верификация решений инженерно-графических заданий.

В настоящей работе будет приведен обзор систем автоматической и автоматизированной проверки инженерно-графических заданий, обобщена задача автоматической проверки и показан общий подход к созданию систем автоматической проверки инженерно-графических заданий.

Обзор систем проверки инженерно-графических заданий

1. В работе В. В. Кислякова и С. В. Осовеца [2] (2000) сообщается о применении программного комплекса для решения и проверки заданий по начертательной геометрии. Комплекс работает под управлением операционной системы MS-DOS и состоит из четырех блоков — блока представления начального условия, рабочего редактора, блока контроля и демонстрации правильного решения. К сожалению, в статье не приведена методика автоматической проверки и копии экранов действующей системы.

2. В работе В. В. Карабчевского [3] (2002) показана методика автоматической проверки решений заданий по начертательной геометрии средствами системы AutoCAD. Для примера выбрана задача построения проекций перпендикуляра к плоскости общего положения (рис. 1, а). Проверку выполняет программа на языке AutoLISP, которая вычисляет координаты отрезков (проекций перпендикуляра), просит пользователя указать построенные им отрезки и сравнивает координаты с эталонными. Система корректно справляется с ситуацией, когда проекции фигур смещены: «для сравнения результата, полученного пользователем, с результатами расчета, следует откорректировать значения точек, задающих начала и концы отрезков, указанных пользователем... так как данные о примитивах хранятся в мировой системе координат, начало координат на эпюре Монжа может быть произвольно расположено на плоскости XY мировой системы координат».

Недостатки методики: при решении пользователь не обозначает проекции перпендикуляра, а система не проверяет обозначений; проекции перпендикуляра должны строиться как отрезки, хотя среди инструментов есть и другие фигуры — прямые, лучи; проверка «чувствительна» к направлению отрезков.

3. В пособиях С. А. Задруцкого и др. [4] (2003) и [5] (2006) показан редактор (рис. 1, б) геометрических моделей RZNG (DrawCAD) для самостоятельного тренажа и контроля навыков решения задач начертательной геометрии. Редактор предоставляет студенту набор инструментов (точки, отрезки, окружности) для проекционного моделирования. Параметры фигур вводятся с клавиатуры (в режиме командной строки). Выбор объектов и построение некоторых из них может выполняться визуально.

В контрольном режиме студент открывает исходные данные задачи и решает ее при помощи ограниченного числа команд, этим обеспечивается совпадение верно построенных фигур с эталонными. Система проверяет решение, если результатом построений является точка, отрезок или фигура, состоящая из точек и отрезков. Формулировки задач не предполагают альтернативных решений. Обозначения добавляются автоматически и не требуют проверки.

4. В работе А. Н. Губанова [6] (2003) демонстрируется работа модуля (рис. 1, в) для решения и автоматической проверки на примере задачи об определении натуральной величины плоской фигуры методом прямоугольного треугольника. Трехмерные модели точек и отрезков представлены в интерфейсе системы проекциями — видами и аксонометрией. Проверка осуществляется на основе сравнения координат точек и длин отрезков с заданным порогом точности, причем, сравнение трехмерных фигур осуществляется отдельно, плоских — отдельно. Для проверки в эталон включены все возможные плоские треугольники. Правильно построенным считается треугольник, если он совпадает с любым из эталонных. Проверка обозначений в системе не предусмотрена.

5. В пособии Ц. Ц. Доржиева [7] (2004) на примере задачи построения линии пересечения двух поверхностей показывается методика, в которой решение строится в режиме вопрос-ответ: система задает вопрос — просит построить фигуру либо указать фигуру на экране, студент — строит или указывает. Методика также основывается на использовании связки системы AutoCAD и языка программирования AutoLISP.

6. В монографии Ю. В. Савельева [8] (2005) показывается обучающая система по начертательной геометрии, работающая на принципе деления задачи на этапы. Переход от этапа к этапу происходит при выборе правильного действия из списка, в случае ошибки студент вынужден возвращаться на предыдущий этап и повторять попытку.

7. В работе S. Isotani, L.O. Brandao [9] (2008) рассматривается использование системы динамической геометрии iGeom (рис. 1, г), которая позволяет строить графические модели (конструкции) на плоскости из точек, прямых и окружностей, использовать измерения и некоторые аффинные преобразования и проверять конструкции учеников. Система предназначена для задач планиметрии. Создание проверяющей модели включает в себя следующие шаги:

1) построение фигур;

2) указание фигур, считающихся исходными;

3) указание фигур, которые требуется построить в задании;

4) указание команд, которые ученик может и не может использовать;

5) сохранение задачи.

Проверка правильности построенной учеником конструкции осуществляется в результате выполнения двух процедур — установления соответствия между проверяемой и проверяющей (template) конструкциями и расчета расстояния между ними. Вычисление расстояния основано на том, что всякая фигура представляется кортежем из n величин, причем, расстояние можно искать только между фигурами одного класса. В этом случае расстояние между фигурами вычисляется как линейное расстояние в n-мерном евклидовом пространстве. Расстояние между фигурами разных классов считается равным +∞.

При установлении соответствия выбираются пары фигур из проверяемой и проверяющей конструкций, находящиеся на наименьшем расстоянии. Фигуры, для которых соответствие установлено, убираются из конструкции, и процесс повторяется до установления соответствий всех фигур.

Расстояние между конструкциями рассматривается как сумма расстояний между соответствующими элементами конструкций. Эквивалентными считаются конструкции, расстояние между которыми равно 0. Правильными — расстояние между которыми лежит в пределах допуска ε. Для проверки параметрических связей конструкция сдвигается и проверка повторяется. Если параметрические связи соответствуют эталону, — сдвиг не изменяет расстояния, в противном случае проверяемая конструкция содержит ошибки.

8. В работе А. Л. Хейфеца [10] (2010) (рис. 1, д) рассматривается автоматизированный коллоквиум на базе системы AutoCAD и программ AutoLISP для проверки решений задач трехмерного моделирования. После получения задания студент отвечает на четыре вопроса — «ответ на каждый вопрос требует выполнения геометрических построений... построив искомый объект... студент указывает его курсором».

9. В работе А. С. Бобровских [11] (2011) предложена методика проверки и язык описания алгоритмов задач начертательной геометрии. Методика сводится к тому, что в базе данных хранится алгоритм решения задачи. Он может быть воспроизведен системой визуализации, то есть использоваться в режиме демонстрации решения задачи. Алгоритм также может использоваться в качестве эталонной последовательности при проверке действий обучаемого. Предполагается пошаговый контроль действий пользователя, подкрепленный изображением, формируемым визуализатором.

10. В работах Ю. В. Полозкова, В. И. Луцейковича, Д. Г. Козинеца (2011) [12, 13] предлагается методика организации решения и проверки графических моделей на базе создаваемого редактора (рис. 1, е). Информационная структура модели содержит уровни: чертеж — область — плоскость проекций — примитив. В качестве примитивов выступают точки, отрезки, прямые, окружности и дуги, сплайны. Для обеспечения сравнения «все изображения жестко связаны с используемой системой координат». Применяются два метода проверки результатов:

1) метод проверки заранее заданных условий подразумевает использовать «именованные объекты (точки), координаты которых известны»;

2) метод сравнения векторных изображений основан «на сравнении координат точек и единичных отрезков, из которых состоит изображение».

Система проверки работает с плоской моделью, закрепленной в поле редактора позиционно и метрически. Обозначения фигур не предполагаются.

11. В работах K. Goh, S. Shukri, R. Manao [14, 15] (2013) развивается идея проверки графических моделей общего вида, создаваемых в CAD-системах, на основе анализа графических файлов (DXF), которые, для удобства проверки должны быть преобразованы в более компактный и подходящий для извлечения параметров фигур формат SVG. Сравнение модели с эталонной осуществляется подобно тому, как это показано в работе S. Isotani, L.O. Brandao.

Сравнительные характеристики систем проверки приведены в таблице 1. Анализ работ показывает, что имеется два основных подхода — использование CAD-редактора (AutoCAD и язык программирования AutoLISP) (2, 5, 8) или разработка собственного редактора (1, 3, 4, 6, 7, 9, 10, 11). В некоторых работах осуществляется пошаговая проверка (5, 6, 9), при этом основу проверки составляет сравнение выполненной студентом команды с командой, определенной на текущем шаге алгоритма. В системах, осуществляющих проверку результата решения (3, 4, 7, 8), студент имеет дело с заранее подготовленным исходным пространством (плоским или трехмерным), выполняет построения в соответствии с заданием. Основу проверки составляет сравнение характеристик эталонных и построенных фигур. В системе (4) модель содержит одновременно плоские и трехмерные фигуры, а сравнение осуществляются в пределах заданной точности. В работе (8) исходные данные упражнений генерируются случайным образом. В работе (7) операция сравнения заменяется на вычисление расстояния между проверяемой и эталонной моделью. В работах (3) и (7) проверка обозначений не требуется, поскольку фигуры обозначаются по мере их построения.

Наиболее значительные результаты демонстрируют системы (3), (7) и (10), в которых реализованы обобщенные принципы и отработана методика автоматической проверки.

В ИГЭУ исследования по автоматизации контроля решения графических задач началась в 2001 году. Студенты старших курсов В. Сосновиков и М. Крылов под методическим контролем Е. П. Милосердова разработали систему для решения задач начертательной геометрии, работающую подобно системе (6): алгоритм решения задачи был представлен графом, на каждом шаге студент выбирал действие из списка и, если выбор делался правильно, переходил к следующему шагу. Недостатком подхода была ограниченность числа шагов (в отличие от реального процесса решения, где возможно выполнение любых построений) и необходимость дополнять список действий ошибочными альтернативами.

В 2002 году автором настоящей работы был предложен вариант геометрического редактора на основе списка команд и архитектура системы автоматической проверки позиционных задач начертательной геометрии. Был создан прототип системы с текстовым интерфейсом для MS-DOS, затем — с оконным интерфейсом (рис. 2, а). В 2003 году была создана система проверки навыков решения (рис. 2, б), которая включала в себя редактор задач (с расширенным набором инструментов и возможностью сохранения задач в базе данных) и систему контроля (с сокращенным набором команд и возможностью загрузки задач из базы данных).

В процессе решения студент выбирал команды из списка и указывал их параметры (обозначения добавлялись автоматически). При этом он мог строить любые точки, прямые, отрезки и решать задачу способом, наиболее приближенным к реальному процессу решения [16]. Система преобразовывала проекции в объекты трехмерного пространства, контроль правильности осуществлялся сравнением с эталонными фигурами. Имелась возможность проверять задачи с альтернативными правильными результатами.

Опыт использования системы показал, что «трехмерность» проверяемой модели затрудняет обобщение методики на метрические задачи (например, в методе прямоугольного треугольника создаются фигуры, которые не принадлежит моделируемому трехмерному пространству) и задания с заменой плоскостей проекций. Кроме того, было принято решение развивать методы автоматической проверки, ориентируясь на интернет-технологии для последующего внедрения в системы с удаленным доступом.

В 2008 году была разработана методика проверки решений, представленных в виде истории команд-построений на плоскости [17, 18]: проверка выполняется системой геометрического доказательства на основе шаблонов — параметрических описаний, автоматизирующих структурный анализ истории команд и позволяющих системе «узнавать» шаги алгоритма решения. В 2011 году была разработана методика проверки решений заданий с лекальными кривыми, в частности, заданий на построение проекций линии пересечения поверхностей.

Практическая реализация была отложена ввиду отсутствия подходящего геометрического редактора, который мог бы быть внедрен в интернет-страницу.

Проведенный анализ систем показывает, что до сих пор не решены проблемы проверки метрических задач, заданий на преобразование чертежа, заданий с поверхностями и развертками и др.

Таблица 1. Характеристики систем автоматического контроля навыков решения графических заданий

Обобщение задачи автоматической проверки решений инженерно-графических заданий

В соответствии с классификацией [20] задача проверки инженерно-графического задания может считаться формальной только для частных случаев, в общем же, ее следует считать неформальной. Поэтому первым шагом к решению задачи автоматизации стало описание процесса проверки преподавателем (рис. 3, а).

Решение студента и условие задачи используются преподавателем для формирования ментальных проверяемой и эталонной моделей. Грубые ошибки в решении обнаруживаются еще на этапе формирования ментальной модели, нарушая ее целостность. Ментальные модели сравниваются, и выявляются ошибки. Сравнение может осуществляться непосредственным соотнесением эталонного образа с проверяемым (при наличии образца), последовательным определением свойств отдельных элементов по признаку да/нет (к примеру, при проверке проекций точки пересечения прямой и плоскости такими свойствами являются принадлежность точки прямой и плоскости) либо выявлением заданной последовательности построений (шагов алгоритма). Проверка включает в себя комплекс процедур распознавания образов, формирования пространственной модели, в общем случае, пространства иной размерности, чем пространство фигур языка описания моделей, соотнесения моделей между собой, формализация результатов в виде оценки.

Таким образом, для решения задачи автоматической проверки необходимо рассмотреть вопросы представления геометрической модели (язык модели) и сравнения геометрических моделей.

1. Представление решений инженерно-графических заданий

В книге Б. И. Аргунова и М. Б. Балка, посвященной построениям на плоскости [21], дается определение задачи на построение, для решения которой «требуется построить … некоторую фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры». Это определение легко обобщается на пространство более высокой размерности. Решением инженерно-графической задачи будем считать геометрические модели, формируемые в процессе решения.

Конструктивно-геометрической моделью будем называть пятерку M=(E, O, R, A, G) , которая включает множество O геометрических объектов пространства E и отношений R между объектами, определяющих структуру модели, причем каждый объект из O отнесен к какому-либо и только одному элементу из A, называемого алфавитом, а каждое отношение из R отнесено к какому-либо и только одному элементу из G, называемого грамматикой.

Будем считать, что построение осуществляется в соответствии с принципами формирования геометрической модели [22]: «на выбранные непроизводные фигуры накладываются геометрические отношения, объединяющие их в составные фигуры». В некоторых случаях геометрические отношения используются только на этапе определения параметров фигуры (параметры прямых при определении координат общей точки), но не включаются в саму модель, поэтому будем различать две формы представления фигур в модели — статическую и динамическую.

Статическое представление фигуры — это определение ее перечислением значений параметров (формы и положения). Динамическое представление фигуры — это определение ее перечислением параметров и отношений, связывающих фигуру с другими фигурами.

Преобразование динамического представления в статическое будем называть редукцией. Очевидно, редукция возможна лишь в случае, если все фигуры, с которыми данная связана отношениями, представлены статически и отношения допускают формирование фигуры. Статическими будем называть фигуры, представленные статически и динамически, если их представление может быть редуцировано. Динамическими фигурами (системами) будем называть фигуры, представленные динамически, и представление которых не может быть редуцировано.

Модели, создаваемые в параметрических САПР, представляют собой динамические фигуры. Если модель, формируемая в геометрическом редакторе, не параметрическая, то выполнение команд представляет собой пошаговую редукцию динамического представления (параметры команды) в статическое (параметры фигуры).

В истории развития методов автоматизации инженерно-графических работ можно выделить два этапа: автоматизация с использованием языков программирования в период 60-80-х годов, нашедшая отражение в инженерно-графическом образовании появлением учебных пособий типа [23], и широкое внедрение систем автоматизации проектирования после появления в начале 80-х годов первой версии редактора AutoCAD. Следовательно, геометрическая модель может быть представлена как программа на некотором языке программирования либо в виде файла в формате геометрического редактора. Форматы редакторов реализуют так называемое векторное представление геометрических фигур, которое восходит к понятию дисплейного файла [24, 25], т. е. представляет собой «программу дисплейного процессора», — поэтому обе формы представления моделей можно считать эквивалентными. Тем не менее, необходимо ввести ограничение: будем рассматривать такие геометрические программы высокого уровня, которые не содержат в явном виде иных инструкций (вычислительных, управления ресурсами и др.), кроме операторов построения фигур. Этому определению вполне соответствуют файлы геометрических редакторов.

2. Сравнение геометрических моделей

Целью сравнения является установление факта совпадения (Ф_э ≡ Ф) или равенства (Ф_э  Ф) фигур. Традиционным способом такого сравнения в геометрии еще со времен античности служит способ совмещения (наложения): здесь условием равенства фигур является возможность отображения точек одной фигуры на другую. Так как число точек большинства фигур бесконечно, на практике применяют различные условия равенства: сравнение координат точек, длин отрезков, мер углов и др.

Пусть дана эталонная модель T = (E_T, O_T, R_T, A_T, G_T) и модель S = (E_S, O_S, R_S, A_S, G_S), требующая проверки. Размерность пространств, алфавит и грамматика, в общем случае, различны. Множества R_S и G_S могут быть пустыми (простое перечисление фигур). Система автоматической проверки должна осуществить сравнение S с T.

Сравнение состоит в установлении соответствия проверяемой модели S и эталонной модели T и выявлении качественных и количественных различий между ними. Источниками различий служат элементы модели S (фигуры или связи), противоречащие эталону, и элементы модели T, отсутствующие в S. Проверяемая модель правильна, если соответствие является отображением T в S, и среди объектов в S, не имеющих прообразов в T, нет каких-либо ошибок.

В общем виде автоматическая проверка конструктивно-геометрической модели представляет собой совокупность трех процедур (рис. 3, б):

1. предварительное преобразование проверяемой модели S в промежуточную модель S', которое может иметь целью восстановление связей, потерянных при сохранении модели в графическом редакторе, структурный анализ и выделение фигур из групп примитивов, преобразование в модель с пространством большей или меньшей размерности;

2. предварительное преобразование эталонной модели T в промежуточную модель T', в результате которого размерность пространств эталонной и проверяемой моделей станет одинаковой; например, в работе (2) В. В. Карабчевского осуществляется преобразование T в T' — трехмерные координаты точек A, B, C, D служат для расчета координат эталонных отрезков проекций перпендикуляра.

3. установление непрерывного соответствия между пространствами E_T' и E_S', в результате чего становится возможным установление соответствия между моделями S' и T', которое, в общем случае, предполагает поиск для всякого объекта в O_T' образа в O_S', и для всякой связи в R_T' соответствующей в R_S'. Если для какого-то объекта или связи образ не может быть найден, отображение считается неполным и свидетельствует о неправильности (полной или частичной) модели S.

Соответствие объектов и связей в S' и T' подразумевается сложным и производится с учетом, как геометрических (соответствие значений параметров формы и положения), так и целого ряда дополнительных свойств. Инициатором установления соответствия является эталонная модель T, которая находится в полном распоряжении разработчика, и создается таким образом, чтобы содержать минимальное достаточное число фигур. Это позволяет довольно гибко выбирать фигуры или даже группы фигур в проверяемой модели в качестве образа.

В свете доклада А.Л. Хейфеца "Геометрическая точность компьютерных алгоритмов конструктивных задач" необходимо дать также теоретическое обоснование возможности автоматической проверки. Пусть задание состоит в построении фигуры А, связанной совокупностью отношений с фигурами a, ..., n.

Необходимое условие: Задание следует считать решенным в том случае, если построенная студентом фигура имеет наименование А и модель содержит указанные отношения либо они могут быть выведены из совокупности имеющихся отношений.

Следствие. Проверить правильность решения возможно лишь при условии, что язык моделирования содержит фигуру А, все фигуры a, ..., n, и все соответствующие отношения и правила вывода.

Ни одна из систем, приведенных выше в качестве примера не удовлетворяет необходимому условию, кроме (7). О методе проверки на основе анализа отношений подробнее в [18].

Будем искать более мягкое условие, достаточное для верификации.

Достаточное условие. Если все фигуры a, ..., n - статические, тогда могут быть определены значения всех параметров фигуры А в результате редукции. Задание следует считать, в принципе, решенным, если построенная студентом фигура имеет наименование А и подходит по параметрам к эталону.

Условие основывается на том, что практическая составляющая задания состоит в построении именно этой фигуры, а каким именно образом она будет получена - неважно. Очевидно, существует шанс случайного построения фигуры А, но предполагается, что им можно пренебречь. Однако уже в такой формулировке можно назвать примеры, когда формально правильное решение система отвергнет (окружность, составленную из кусков сплайна Безье) или когда неправильное решение совпадет с ответом (на одной из олимпиад студент нашел нужную точку, просто поделив отрезок на три части, хотя требовалось использовать довольно сложные отношения).

Тем не менее и такая формулировка не позволяет проверять задания, например, на построение лекальных кривых. Так, линия пересечения двух поверхностей второго порядка - алгебраическая кривая четвертого порядка - отсутствует в языке моделирования геометрических редакторов. При решении задания студент скорее всего использует сплайн, то есть фигуру иную, нежели А. Ни о каком точном соответствии параметров говорить нельзя, поэтому введем особый вид фигур - сложные, в отношении которых будем считать, что фигуры совпадают, если совпадают все контрольные точки и некоторое число промежуточных точек находится в непосредственной близости (в пределах допуска).

Во всех случаях возможность проверки решения обеспечивается тем, что предварительно доказано (разработчиком эталона), что именно фигура А является решением.

3. Автоматизация сравнения моделей

Проверку осуществляет проверяющая машина (термин машина употреблен по аналогии с геометрической машиной в [26]).

Проверяющая машина — совокупность данных и алгоритмов, устанавливающая соответствие проверяемой модели эталону, информационная структура которой может быть представлена в виде кортежа (P_O, F_O, P_R, G_R, V), где P_O — словарь алфавита, множество троек вида (aⁱ_Т', a^j_S', fⁱ), aⁱ_Т', a^j_S' — соответственно, элементы алфавитов A_T' и A_S', а fⁱ — оператор сопоставления, F_O — множество таких операторов, P_R — словарь грамматики, множество троек вида (rⁱ_Т', r^j_S', gⁱ), где rⁱ_Т', r^j_S' — соответственно, элементы грамматик G_T' и G_S', а gⁱ — оператор сопоставления, G_O — множество таких операторов, V — собственные атрибуты проверяющей машины, управляющие порядком ее работы.

Обобщенный алгоритм проверки наложением:

1. Осуществляется сортировка объектов O_T' и выделяется список B_T' таких, которые могут быть использованы для вычисления преобразования пространства E_T'.

2. Для каждого b_i в B_T' b_i помечается и в соответствии с тройкой (b_i , aⁱ_S', fⁱ) выполняется поиск кандидата oⁱ_S' в O_S', кандидат помечается; пара (b_i, oⁱ_S) добавляется в определитель преобразования.

3. Если определитель не полон, шаг 2 повторяется.

4. Если определитель полон, вычисляются параметры преобразования.

5. Для каждого не помеченного в O_T' объекта a_i в соответствии с тройкой (a_i, aⁱ_S', fⁱ) выполняется поиск кандидата oⁱ_S' такого, что вычисление оператора fⁱ(a_i, oⁱ_S') подтверждает отображение (с ошибкой или без).

6. Если кандидат найден, то oⁱ_S' помечается.

7. Если кандидаты исчерпаны или отображения выполнены с ошибками, но есть еще тройки (a_i, aⁱ_S', fⁱ), шаг 5 повторяется для следующего подходящего символа алфавита aⁱ_S'.

8. Если кандидаты и тройки исчерпаны и ни один объект не помечен, то a_i добавляется в список объектов, отображенных с ошибками, шаг 5 повторяется для следующего элемента эталонной модели.

9. Для каждого отношения r_i из R_T' проверяется, найдены ли образы объектов o_j и o_k.

10. Если образы не найдены, отношение r_i добавляется в список ошибок, и выполняется шаг 9 для следующего отношения.

11. Если образы найдены, то в соответствии с тройкой (r_i, rⁱ_S', gⁱ) выполняется поиск отношения rⁱ_S' связывающего образы объектов o_j и o_k, и вычисляется оператор gⁱ(r_i, rⁱ_S').

12. Если проверяемая модель не содержит ни одного явного отношения (G_S=, R_S=), то система пытается реконструировать отношение rⁱ_S для объектов o_j и o_k: rⁱ_S'= recon (r_i, o_j, o_k). Если это возможно, то вычисляется gⁱ(r_i, rⁱ_S'), если нет — отношение r_i добавляются в список ошибок, и выполняется шаг 9 для следующего отношения.

13. По результатам вычисления отношение помещается либо в список успешно отображенных, либо в список отображенных с ошибкой. Затем следует выполнение шага 9 для следующего отношения.

14. Если список B_T' не пуст, то возможно повторение шагов 4-13 для новых параметров отображения.

4. Проверка некоторых задач

Широкий круг задач начертательной геометрии может быть проверен с использованием простого метода наложения (что и демонстрировали системы (2), (3) и автора настоящей работы). На рис. 4, а показан чертеж и проверяющая модель задачи пересечения прямой и плоскости. Проверяющая модель состоит из проекций точек M₁, M₂ и четырех лучей (основная и штриховая линия на двух видах). Начало координат и ось сохранены в качестве определителя преобразования. Прочие объекты чертежа, кроме точек и кусков прямой, при проверке считаются «лишними» и игнорируются.

Самым простым примером динамической фигуры (системы) является безосный чертеж. Будем называть модели комбинированными, если фигуры множества O такой модели относятся к разным системам отсчета. Фигуры множества O комбинированной модели можно разделить на классы так, что фигуры каждого класса относятся к своей системе отсчета. Множество фигур делится на компоненты и соответствие устанавливается покомпонентно. При этом для каждой компоненты определяется собственный определитель преобразования. Пример проверяющей и проверяемой модели задачи с безосным чертежом приведен на рис. 4, б. Здесь индексы проекций среди атрибутов фигур используются для разделения модели T на видовые компоненты: в состав видовой компоненты включаются фигуры с соответствующим индексом и фигуры, связанные отношениями только с фигурами компоненты. При проверке задачи определителем отображения первой компоненты выступает проекция A₁, второй — A₂. Виды могут быть произвольно смещены вверх или вниз.

В ряде случаев выгодно использовать проверяющую модель в пространстве иной размерности, чем проверяемая. В этом случае эталонная либо проверяемая преобразуется.

Например, плоский эталон не позволяет проверить чертежи задач на построение прямой и плоскости параллельно заданной плоскости (рис. 4, в). Проверка может быть выполнена, если применять трехмерную эталонную модель. Проверяемая модель S преобразуется следующим образом:

1. Объекты-проекции с одинаковыми именами объединяются в именованные группы (на рисунке — A (A₁, A₂), B (B₁, B₂) и т д.).

2. Выполняется обратная задача начертательной геометрии — формирование пространственных фигур (A, B, M и др.) на основе проекций.

G_S' и R_S' оставляются пустыми.

В ряде случаев более выгодно преобразование проверяющей модели T. Так, при проверке аксонометрических проекций трехмерная проверяющая модель отображается в плоскую модель T’ и устанавливается соответствие с S. На рис. 4, г показана четверка некомпланарных точек эталона (A-D), которая используется в качестве определителя преобразования.

5. Особенности применения реальных языков описания моделей

Модель, созданная в какой-либо реальной системе геометрического моделирования представляется предложениями соответствующего языка. Это создает ряд дополнительных трудностей обработки таких моделей.

Первая проблема связана с особенностями языка моделирования: 1) одна и та же фигура в языке реальной системы моделирования может быть представлена несколькими способами, 2) не все фигуры реальной системы моделирования представлены в том виде, как это удобно для автоматической проверки (например, фигурой, наиболее близкой к традиционному изображению прямых в начертательной геометрии, в геометрических редакторах является отрезок; что создает коллизии — отрезок проверяемой модели может быть отрезком, лучом или прямой), 3) некоторые фигуры задач в реальных системах моделирования отсутствуют и составляются из групп фигур, имеющихся среди инструментов редактора (например, фигура проекция точки представляется окружностью, областью заливки внутри окружности, двумя текстовыми полями — названием и индексом проекции), 4) многие языки реальных систем моделирования (например, DXF) не содержат средств для представления связей (их можно восстановить, например, принадлежность, касание, но нельзя с уверенностью утверждать, что особое расположение фигуры заняли не вследствие какой-либо случайности).

Перечисленные трудности относятся к категории задач распознавания образов, для их преодоления применяются две стратегии:

1) восходящий разбор — анализ фигур, составляющих проверяемую модель (на языке реальной системы моделирования), выделение групп и объединение их в символы, соответствующие фигурам эталонной системы, анализ геометрических свойств фигур и восстановление утерянных связей — принадлежность, параллельность, перпендикулярность, касание и др.; восходящий разбор является частью преобразования S в S';

2) нисходящий разбор — анализ фигур, составляющих эталонную модель и целенаправленный поиск среди фигур проверяемой модели (на языке реальной системы моделирования) групп, соответствующих эталонным фигурам, и атрибутов у фигур, соответствующих эталонным связям.

Вторая проблема связана с разработкой эталонных моделей, которые должны быть представлены на некотором идеальном языке. Программирование их вручную затруднительно, и, фактически, требуется особый геометрический редактор. Разработка такого редактора сама по себе чрезвычайно сложна. В качестве промежуточного решения можно использовать набор инструментов CAD-системы, расширенный фигурами, приближенными к предметной области. Подобное расширение допускает в настоящее время любая CAD-система (блоки в системе AutoCAD, фрагменты — в Компасе и др.). Вставка их в эталонную модель транслируется в соответствующие символы языка (внешний вид фигур-заместителей при этом не обязательно соответствует каким-либо требованиям или стандартам). Преобразование таких моделей в эталонные является частью преобразования T в T'.

Заключение

Результаты исследования позволили создать систему автоматической проверки чертежей в формате DXF [27]. Пример проверяющей модели и сгенерированный системой чертеж для решения приведены на рис. 2, в-г. Проверку осуществляет php-модуль, внедренный в состав интернет-системы. Эталоны создаются в редакторе AutoCAD с применением специальных блоков — проекция точки, прямой, плоскости и др. Чертеж задачи создается «на лету» удалением всех фигур из слоев результата и промежуточных построений. Решение (тоже в формате DXF) должно быть загружено в интернет-систему, где мгновенно выполняется проверка.

Достоинства: не нужно разрабатывать графический редактор, доступны все инструменты мощного редактора, эталон создается в том же редакторе, при создании эталона и при решении есть возможность использовать специальные блоки, в одном DXF файле можно разместить несколько заданий - получается одна комбинированная задача.

Практика показала и недостатки подхода: сложность интерфейса редактора AutoCAD, необходимость изучения инструментов, которые в значительной мере превышают необходимый в учебном курсе набор, недоступность системы на домашних компьютерах (не у всех была возможность скачать и установить лицензионный AutoCAD), необходимость сохранять в формат DXF вместо DWG, необходимость скачивать и загружать файлы в браузере - помешали достаточно сильно мотивировать студентов к использованию инструмента верификации. Фактически, студенты решали задачи и проверяли себя только в рамках факультативного занятия, но ни один из них не решал задачи дома.

Дальнейшее расширение возможностей системы проверки было приостановлено, в настоящее время ведется разработка визуального геометрического редактора на основе технологий, отработанных при создании тренажеров. Предполагается, что программный код системы проверки без значительных модификаций будет использован в связке с новым визуальным редактором.

При решении задачи автоматизации применен достаточно общий подход, что позволяет использовать основной алгоритм и методы для автоматизации проверки решений других классов заданий.

Выводы

Приведен обзор систем автоматической и автоматизированной проверки инженерно-графических заданий.

Исследованы вопросы автоматизации проверки.

Составлен алгоритм проверки конструктивно-геометрических моделей наложением.

Показано применение алгоритма для проверки заданий начертательной геометрии.

Разработана система автоматической проверки DXF файлов для работы в составе интернет-системы.

Список литературы

1. Бойков А. А. Верифицируемость инженерно-графических задач как необходимое условие эффективной самостоятельной работы. URL: http://dgng.pstu.ru/conf2016/papers/68/ (дата обращения: 17.03.2016)

2. Кисляков В. В., Осовец С. В. Программный комплекс для постановки и решения задач по начертательной геометрии. ОТИ МИФИ. // Электронная конференция ЭНИТ-2000, 17-19 мая, Ульяновск (Россия). URL: http://masters.donntu.org/2004/fvti/proglyadova/library/article3.htm (Дата обращения: 17.01.2016)

3. Карабчевский В.В. Автоматическая генерация решения задач начертательной геометрии как средство формирования эталонов в подсистеме тестирования. // Научные труды Донецкого национального технического университета. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" (МАП-2002). Выпуск 52: Донецк: ДонНТУ, 2002. 248 с.

4. Задруцкий С. А. Решение задач по начертательной геометрии графоаналитическим способом с применением ПЭВМ / С. А. Задруцкий, А. А. Резанко, В. А. Столер. Минск: БГУИР, 2003. 52 с.

5. Решение задач по начертательной геометрии с применением ПЭВМ (программа DrawCAD) / С. А. Задруцкий [и др.]. Минск: БГУИР, 2006. 52 с.

6. Губанов А. Н. Автоматизированная система обучения основам геометрического моделирования в САПР : дис. ... канд. техн. наук : 05.13.12. Самара, 2003. 135 с.

7. Доржиев Ц. Ц. Разработка и методические рекомендации по применению автоматизированной обучающей системы (АОС) по начертательной геометрии в учебном процессе. Улан-Удэ: Издательство ВСГТУ, 2004. С. 36-43

8. Савельев Ю. В. Вычислительная графика. Екатеринбург. 2005. С. 102-106.

9. Isotani, S. An algorithm for automatic checking of exercises in a dynamic geometry system: iGeom / S. Isotani, L.O. Brandao // Computers & Education. 2008. Vol. 51. pp. 1283-1303.

10. Хейфец А. Л. Автоматизированный коллоквиум как новая форма контроля знаний по графическим дисциплинам. URL: http://dgng.pstu.ru/conf2010/papers/39/ (Дата обращения: 17.03.2016)

11. Бобровских А. С. Разработка обучающей системы для алгоритмов начертательной геометрии с использованием технологии автоматного программирования // Вестник компьютерных и информационных технологий. М.: Машиностроение, 2011. № 1. С. 38-43

12. Козинец, Д. Г. Программно-методический комплекс поддержки процесса графической подготовки и контроля знаний по начертательной геометрии / Д. Г. Козинец, Ю. В. Полозков // Инновационные технологии в инженерном образовании: материалы междунар. науч.-практ. конф., Минск, 27–28 апр. 2011 г. Минск, 2011. С. 247-249.

13. Полозков Ю. В., Луцейкович В. И. Концепция интерактивного программного комплекса обучения и контроля знаний по начертательной геометрии // Вестник Полоцкого государственного университета. Серия E. 2013. №15. С. 48-57

14. Goh K., Shukri S., Manao R. Automatic Assessment for Engineering Drawing. J. Soft Computing and Software Engineering. 2013. pp. 497-507.

15. Goh K., Manao R. Assessing engineering drawings through automated assessment: discussing mechanism to award marks // International Journal of Smart Home. 2013. Vol. 7. No.4. pp. 327-336.

16. Бойков А. А., Милосердов Е. П., Федотов А. М. Средства компьютерного обучения графическим дисциплинам // Проблемы научно-методического и организационного обеспечения учебного процесса по начертательной геометрии, инженерной и компьютерной графике: сборник трудов Всерос. семинара-совещания заведующих кафедрами графических дисциплин. Саратов: СГТУ. 2005. С.27-29.

17. Бойков А. А. Разработка методов обучения и контроля в автоматизированном учебном комплексе. // Вестник компьютерных и информационных технологий. М.: Изд-во «Машиностроение», 2008. №7. С. 47- 49.

18. Бойков А. А., Федотов А. М. Применение шаблонов для анализа геометрических построений при решении задач начертательной геометрии в автоматизированной системе // Вестник компьютерных и информационных технологий. М.: Изд-во «Машиностроение», 2011. № 3. С. 29-35.

19. Бойков А. А. Построение линий пересечения поверхностей в системе обучения начертательной геометрии // Сборник научных трудов Международной научно-технической конференции «Состояние и перспективы развития электротехнологии» (XVI Бенардосовские чтения). Т. 3. Иваново. 2011. С. 366-368.

20. Котов И. И. Алгоритмы машинной графики / И. И. Котов, В. С. Полозов, Л. В. Широкова. М.: Машиностроение, 1977. 232 с.

21. Аргунов Б.И., Балк М.Б. Геометрические построения на плоскости: учебное пособие. М.: ГУПИ Министерства Просвещения РСФСР, 1957. 268 с.

22. Полозов В. С. Автоматизированное проектирование / В. С. Полозов [и др.]. М.: Машиностроение, 1983. С. 28-54.

23. Курс начертательной геометрии на базе ЭВМ / Тевлин А. М. [и др.]. М.: Высшая школа, 1983. 176 с.

24. Гилой В. Интерактивная машинная графика: Структуры данных, алгоритмы, языки. М.: Мир, 1981. 384 с.

25. Ньюмен У., Спрулл Р. Основы интерактивной машинной графики. М.: Мир, 1976. 576 с.

26. Вальков К.И. Введение в теорию моделирования. Л.: ЛИСИ, 1973. С. 67-73

27. Бойков А. А. Тренажер на базе веб-системы и САПР-редактора / Новый университет. Серия: технические науки. Йошкар-Ола: ООО Коллоквиум. 2013. №7. С. 55-57.

Рисунки к докладу

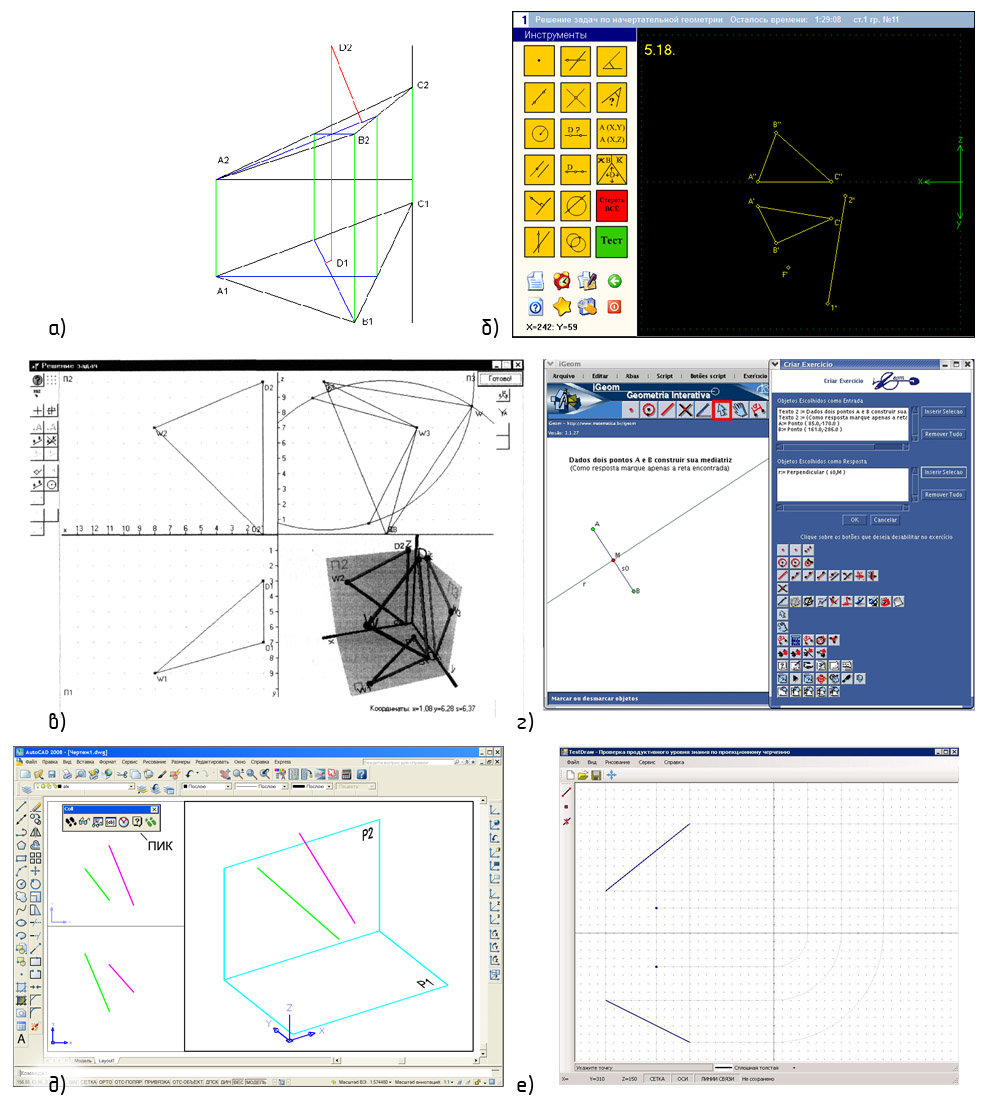
Скриншоты систем автоматической и автоматизированной проверки к обзору

Скриношты систем автоматической проверки

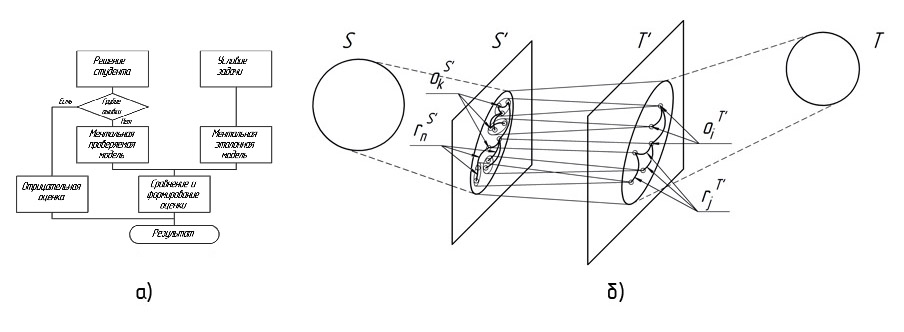
Моделирование процесса проверки решений инженерно-графических задач

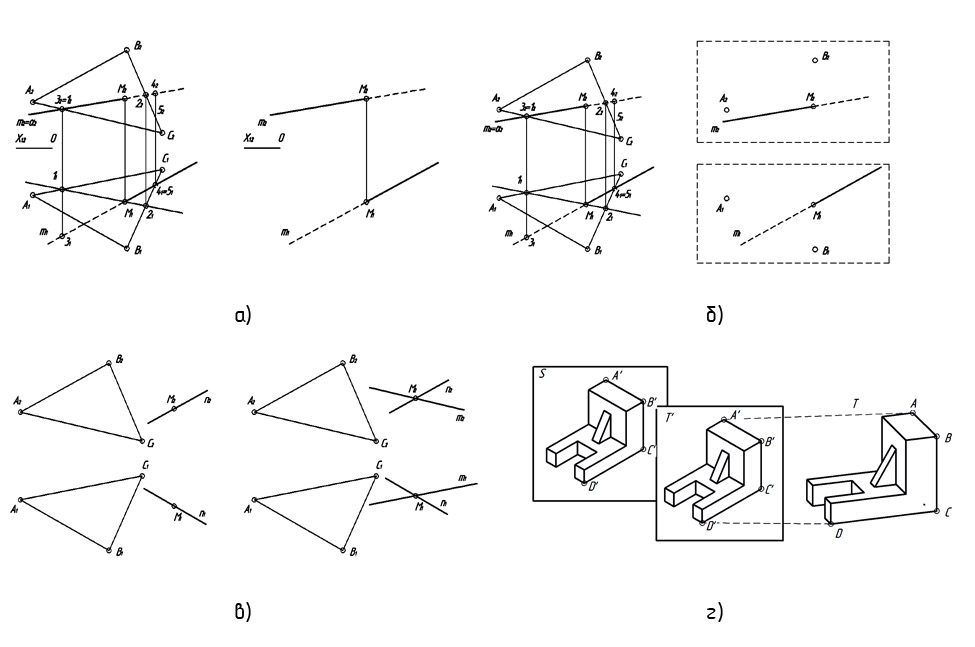
Примеры чертежей и эталонов

Ротков Сергей Игоревич (21 марта 2016 г. 12:14)	Алексей Александрович! Очень интересная статья. Она показывает ваш уровень как состоявшегося научного работника. Ждем вас с докладом по материалам кандидатской диссертации на нашем научном семинаре кафедры и диссертационного совета. С уважением, С.И.Ротков.
Хейфец Александр Львович (21 марта 2016 г. 20:51)	Алексей Александрович, здравствуйте. Автоматизация проверки графических работ является весьма актуальной задачей. Как-то я подсчитывал количество проверяемых задач в семестре. Пусть по НГ в семестре студент решает 50 задач (например, в нашей рабочей тетради столько). Студент предъявляет каждую три раза. В группе на преподавателя 10 студентов. В семестре – 10 групп. Получаем в семестре 50*3*10*10=15000 проверок на преподавателя. Конечно, цифра приближенная и округленная, но впечатляет. Поэтому задача автоматизировать проверку, чтобы реже видеть приятные студенческие лица, давно интересовала преподавателей. Сделанный Вами обзор работ этого направления весьма интересен. Работы начались с появлением компьютеров. В благодарность за фразу “В свете доклада А.Л. Хейфеца…” к литературному обзору Вашей диссертации дарю три еще более ранние работы, в которых возможно впервые изложены идеи автоматизированной проверки графических работ: 1. А.А. И. Королевич. Об алгоритмизации  решения элементарных метрических задач. В.сб.: Прикладная геометрия и инженерная графика. Вып. 1. Киев. 1965. С. 9-15. 2. Е.И. Годик, Л.Б. Курганов. Использование методов алгоритмического характера при составлении обучающих программ по НГ. В.сб.: Прикладная геометрия и инженерная графика. Вып. 17. Киев. 1973. С. 187-190. 3.  Е.Т. Будзинаускене. Использование ЭВМ для генерирования заданий и контроля знаний графических дисциплин в обучающих системах. Сб.: Геометрография. Вып. 2. Рига. 1977. С. 119-125. Дальнейшее Ваше изложение идей автоматизированной проверки весьма мудреное и наукообразное (явно для диссертации). Скажу проще о моей системе, о которой вы положительно отозвались. В ней проверка выполняется сл. образом.  Для графического объекта, полученного студентом, средствами AutoLisp’a из ГБД извлекается список данных, из него – значения параметров. Эти значения сравниваются с результатом вычислений, выполненных компьютером.  Модель генерируется случайным образом – списать невозможно… То есть это не “угадайка”, а действительная проверка графического решения. Подчеркну, что все подобные и известные системы контроля работают в AutoCAD’е, где есть программирование (это аргумент в пользу применения этого пакета). Относительно проверки в формате DXF – не уверен, что это удачное решение, поскольку проверять приходится текстовый файл. Почему не извлекать из ГБД средствами AutoLisp’a? Желаю успешной защиты. Правда, это пожелание было и в прошлом году(?). С уважением. А.Л. Хейфец
Бойков Алексей Александрович (22 марта 2016 г. 22:33)	Уважаемый Сергей Игоревич, спасибо за высокую оценку! Хочу отдельно поблагодарить моего научного руководителя А.М. Федотова. Надеюсь выступить с докладом в апреле. С уважением, А.А.Бойков.
Бойков Алексей Александрович (22 марта 2016 г. 22:52)	Уважаемый Александр Львович, спасибо внимание к моей работе и добрые пожелания! Я очень рад, что в этом вопросе наши точки зрения совпадают.  Работая над докладом, я припомнил, будто видел статью, где давались временные оценки советского периода, сколько времени на проверку заданий тратил преподаватель. Пересмотрел мои архивы - сборники НГиИГ, некоторые выпуски "Прикладной геометрии..." - нашел только оценку труда студентов при решении. При нынешнем базовом образовании необходимость дополнительной проверки только возрастает. Рост объема проверки ведет к уменьшению числа решаемых задач. В нашей тетради - около сотни простых заданий (в том же Фролове - почти триста). Но даже это - колоссальное время, - Ваши цифры это наглядно показывают. Мы проверить все задачи у всех студентов просто не в силах, проверяем только ключевые, а по остальным работаем, по сути, только с теми студентами, кто сам задает вопросы. Насчет проверки в AutoCAD'е. В первой части доклада упоминается, что мы поставили задачу не только автоматизировать проверку, но и реализовать проверку в связке с Интернет-системой. Это накладывает дополнительные ограничения: проверка должна осуществляться на стороне сервера. Вы совершенно правы насчет неудобств DXF. Отдельное спасибо за ссылки.  С уважением, А.А.Бойков.
Горнов Александр Олегович (22 марта 2016 г. 23:12)	Алексей Александрович!   Ожидали   на КГП тезисы  обобщающего доклада, c которым Вам предстоит вскоре выступить . Отмечая  Вашу широкую   научную эрудицию, искренне  желаем  успехов в предстоящих  важных  событиях - научным докладом, завершении   подготовки  и защите  диссертации  на соискание  ученой  степени  кандидата  наук.  А.О.Горнов, Л.А. Шацилло
Бойков Алексей Александрович (23 марта 2016 г. 0:11)	Уважаемые Александр Олегович и Людмила Анатольевна, спасибо за высокую оценку и поддержку! С уважением, А.А.Бойков.