ЭЛЕМЕНТЫ ЯЗЫКА ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ

Рассматривается вопрос создания знаковой системы для записи алгоритмов решения конструктивных задач и некоторые ее приложения.

Введение

Предваряя доклад, отметим, что в настоящее время принятой общей системы обозначения, подобной языку алгебры в аналитической геометрии, которая позволяла бы точно и компактно описывать алгоритмы решения конструктивных задач (задач на построение), не существует.

Известны работы по стандартизации геометрических обозначений в курсе начертательной геометрии [1-3], ряд работ А. И. Королевича посвящен символической записи конструктивных алгоритмов [4-6], различные системы обозначений обобщенных конструктивных алгоритмов используются в трудах и учебных пособиях [7-14] и др. Одновременно с этим необходимость решать конструктивные задачи при помощи ЭВМ сопровождалась появлением своеобразных «гибридов» — языков программирования или библиотек подпрограмм языков программирования [15-18], выполняющих ту же функцию — запись алгоритмов решения задач для повторного и многократного использования.

Так или иначе, наиболее распространенной формой представления алгоритмов решения конструктивных задач остается чертеж, дополненный словесным описанием или геометрическими формулами принадлежности, параллельности, перпендикулярности и теоретико-множественными операциями. В результате — геометрические алгоритмы до сих пор остаются «более громоздки и трудоёмки, чем аналитические» (А.Г. Гирш в обсуждении к докладу [19]).

Успешным примером в отношении создания новой знаковой системы для представления решений конструктивных задач следует считать появление системы «Симплекс» [20-22], предоставляющей, кроме возможности автоматизировать выполнение конструктивных геометрических алгоритмов, новые формы их записи — текстовую и графическую (в виде схемы), тем не менее эти формы не решают всех задач, связанных с представлением конструктивных алгоритмов.

1.

Будем рассматривать в качестве основы теорию геометрических построений [23, 24], согласно которой конструктивные задачи решаются при помощи построений, называемых элементарными, которые применяются к фигурам, называемых данными (исходными), с целью получить фигуры, называемые требуемыми. Последовательности элементарных построений могут соединяться в составные построения и использоваться далее наравне с элементарными. При решении задач возможно использование произвольных фигур.

Таким образом, язык геометрических построений должен решать следующие задачи:

• однозначно указывать на объекты и их типы в тех случаях, когда тип объекта существенен при решении задачи;
• однозначно указывать на элементы фигур (центр окружности, фокус параболы и др.);
• однозначно указывать на построения, элементарные и составные, их взаимосвязь;
• закономерным образом различать экземпляры фигур, если в результате некоторого построения их получается несколько;
• давать возможность выполнять операции над конечными группами элементов (подобно алгебраическим операциям ∑, ∏, min и др.);
• содержать средства работы с числами и возможность производить измерения (измерять и откладывать);
• быть достаточно компактным, без «экзотических» знаков и начертаний.

Отдельные классы задач могут добавлять собственные требования, например, рассматривать геометрические преобразования в качестве построений, коробовые линии (сплайны) в качестве фигур и др., поэтому основа языка должна быть достаточно универсальной для расширений. Отдельной задачей можно считать наличие языковых средств, обеспечивающих визуальное оформление элементов, например, задание типа линии.

2.

В аналитической геометрии, где элементами модели являются числа и формулы, используются две формы задания геометрических объектов — явная (b = f(a)) и неявная (F(a, b) = 0). В первом случае a и b оказываются зависимы, причем a первично; во втором — a и b оказываются равноправны. Аналогом неявной алгебраической формы могут служить геометрические машины, рассматриваемые в [20], основанные на отношениях. В нашем случае ключевым элементом является построение, для которого всегда известны исходные и требуемые фигуры, и более подходящей является явная форма.

Здесь же отметим недостатки традиционных геометрических символов принадлежности, параллельности и др.

Во-первых, в соответствии с теорией параметризации [25, 26] всякая фигура определяется определенным числом величин или условий. Геометрические знаки, наоборот, определяют точно одно условие, и для задания одной фигуры необходимо перечислять их все, что, при необходимости описывать несколько однотипных построений, приводит к крайне громоздкой форме записи.

Во-вторых, геометрические символы не охватывают всех комбинаций параметров и, часто, требуют словесных пояснений, например: с – окружность с центром в точке A, B  c.

2.1. Будем записывать построение как оператор присваивания, подразумевая связывание безымянной геометрической фигуры с некоторым уникальным символом — именем, в следующем виде:

имя = символ построения (формальные параметры)

Такая форма, в целом, соответствует определению конструктивно-геометрической модели решения задачи [27].

Под формальными параметрами будем понимать исходные фигуры построения и дополнительные числовые величины (длины, расстояния, меры углов и пр.). При этом организация формальных параметров возможна одним из двух способов:

• позиционным, при котором порядок следования параметра определяет его роль в построении:

• функциональным, при котором роль параметра указывается явно, а порядок может быть произвольным:

c = окружность (radius=радиус, center=центр);

Здесь и далее будем использовать первую форму ввиду компактности, считая обе формы эквивалентными. Для наглядности будем добавлять в символ построения условные знаки, обозначающие роль параметров в соответствии с порядком перечисления, например:

c = окружностьЦР (Центр, Радиус)

2.2. Будем определять составные построения при помощи конструкции вида:

Список возвращаемых объектов подчиняется тем же правилам, что и список формальных параметров. Например, при наличии элементарного построения окружностьЦР и измерителя расстояниеТТ составное построение окружности по центру и точке может быть определено так:

Здесь число (расстояние между точками) рассматривается как элементарная единица языка наравне с фигурами и связывается с именем d. Поскольку само по себе это расстояние нигде в дальнейшем не применяется, правильнее использовать его напрямую:

c = окружностьЦР (центр, расстояниеТТ (центр, точка) )

Краткая форма определения составных построений выглядит так:

окружностьЦТ (центр, точка) = окружностьЦР (центр, расстояниеТТ (центр, точка) )

2.3. С целью избежать лишнего обозначения промежуточных фигур глубина вложенности построений не ограничивается.

2.4. В результате построения может быть создано несколько объектов. Для групповых операций с конечными наборами объектов предназначены списки:

[элемент1, …]

Например, результатом пересечения прямой с окружностью является пара точек. Использование построения выглядит следующим образом:

[точка1, точка2] = пересечениеОП (окружность, прямая)

Предполагается, что порядок точек не случаен. Так, если окружность совершает незначительное перемещение или изменение радиуса, то новая точка1 окажется в окрестностях старой точки1, а точка2 — в окрестностях старой точки2.

Если один из группы объектов в дальнейшем не требуется, вместо имени используется символ «_»:

[точка1, _] = пересечениеОП (окружность, прямая)

Если какой-то объект группы необходимо использовать при вложении построений используется форма:

пересечениеОП (окружность, прямая){индекс},

где для первого элемента списка индекс равен 0.

2.5. Для ввода в задачу исходных или случайных фигур используется аналитическая форма построения:

объект = построениеXY... (числовые параметры)

Например, построение точки и окружности может быть выполнено так:

A = точкаXY (x_A, y_A)

c = окружностьXYR (x_центр, y_центр, радиус)

При постоянных значениях параметров такие построения полностью эквивалентны графическому заданию, которое следует считать предпочтительным.

2.6. Для обращения к специальным элементам фигур используется символ «.» (точка). Так, пусть c – окружность, тогда «c.центр» – ее центр, «c.радиус» – радиус, «c.диаметр» – диаметр и т. п. Создание подобных конструкций выполняется при помощи символа new:

объект = new (имя1 = построение1, ...)

где элементы «имя1», … оказываются в дальнейшем доступны в форме «объект.имя1»

2.7. Геометрические преобразования (коллинеации или корреляции), как и прочие объекты могут быть заданы набором параметров и могут, в свою очередь, использоваться для построения новых фигур. Рассматриваются именно однозначные обратимые соответствия. Создание объекта-преобразователя общего вида выглядит так:

преобразователь = символ преобразования (формальные параметры)

Прямое преобразование осуществляется следующим образом:

[копия1, …] = преобразовать (преобразователь, оригинал1, …)

Обратное преобразование — следующим:

[копия1, …] = преобразоватьОбр (преобразователь, оригинал1, …)

Для удобства соответственные фигуры до и после преобразования в списке формальных параметров разделяются символом «:», например:

Само преобразование и в том, и в другом случае выполняется аналогично:

Атр = преобразовать (пр1, А)

2.8. Дискретное приближенное решение задач состоит в том, что некоторая группа построений выполняется заданное число раз. Такое выполнение осуществляется при помощи циклической конструкции вида:

Цикл выполняется заданное число раз, при этом объект1 принимает значения из диапазона1, объект2 — из диапазона2 и т. д. Диапазон может быть задан в виде [начало : конец] или [объект], например, цикл:

— строит серию из 10 окружностей с радиусами от 5 до 100 и заданным центром, цикл:

— строит серию из 10 окружностей с заданным центром, проходящих через различные точки окружности1, соответственно. Символ $ используется для генерации имен вида c0 … c9, принимая значение счетчика.

Границы диапазона могут быть, соответственно, […], (…), (…], […). Круглая скобка запрещает выполнение цикла для первого или последнего значения из диапазона. Согласование диапазонов для разных объектов возможно лишь при одинаковом суммарном числе актуальных значений.

Для дискретного представления кривых совместно с циклами используются полилинии, создание которых осуществляется в три этапа — инициализация, добавление точек и актуализация:

Формальные параметры полилинии задают вид объекта — ломаная (0), сплайн (кубический, безье и др.).

2.9. Адаптивная модель кривой.

В конструктивной геометрии имеется несколько способов построения кривых, основанных на использовании какой-то базовой. Некоторые из этих способов могут быть описаны при помощи преобразований (п. 3.7), некоторые используют многозначные (необратимые) соответствия. Для работы с ними введен специальный вид кривой — точечный ряд. Пусть определено построение, осуществляющее отображение некоторой точки A в точку Aq:

Кривая mq, полученная отображением точек базовой кривой m, может быть описана так:

mq = ряд(Aq, m)

2.10. Атрибуты объектов

Атрибуты объекта, в отличие от параметров, имеют описательный, а не геометрических характер. Наиболее важным из них является тип линии. Все множество атрибутов будем связывать с понятием визуального стиля объекта или просто стиля. Задание стиля для фигуры, получающейся в результате построения осуществляется следующим образом:

фигура = построение (параметры) : стиль (атрибуты)

Если в результате построения создается несколько фигур, для каждой из них стиль задается отдельно:

[фигура1, ...] = построение (параметры) : стиль (атрибуты1) : …

3.

Рассмотренные элементы языка геометрических построений достаточно общи и не привязаны к виду и размерности пространства, и могут конкретизироваться объектами и построениями в зависимости от решаемой задачи. Используемые в языковых конструкциях символы просты, так что алгоритмы могут быть набраны в любом текстовом редакторе, но достаточно гибки. Слова «точка», «прямая» и др. в символах построений использованы для наглядности и для того, чтобы показать независимость языковых конструкций от решаемых задач. Любая конкретная система геометрических построений получается введением некоторого набора элементарных построений и конструктивным заданием всех остальных.

3.1. Например, возьмем в качестве элементарных следующие построения: pab – точка на пересечении прямых, sab – отрезок через две точки, sop – прямая перпендикулярно заданной через точку. Этот набор, в целом, соответствует системе построений при помощи угольника. Запишем решение задачи планиметрии о построении центра описанной около треугольника окружности. Даны три вершины A, B, C. Решение — пересечение двух прямых, проведенных из вершин треугольника к точкам пересечения пар соответствующих перпендикуляров [23] (рис. 1, а):

center (P1, P2, P3) = pab ( midline (P1, P2, P3), midline (P2, P3, P1) )

где построение одной из прямых выглядит следующим образом:

Как известно, искомый центр лежит на пересечении срединных перпендикуляров, то есть решение может быть получено иначе:

center (P1, P2, P3) = pab ( midort (P1, P2), midort (P1, P3) )

Получаем конструктивное тождество:

pab ( midort (P1, P2), midort (P1, P3) ) ≡ pab ( midline (P1, P2, P3), midline (P2, P3, P1) )

Поскольку тождество имеет вид pab(a, b) ≡ pab(c, d), прямые a-d принадлежат общему пучку и допустимы их перестановки. Если известна середина отрезка, построение срединного перпендикуляра выглядит так:

midort (P1, P2) = sop( sab (P1, P2), midpoint (P1, P2))

Выполним подстановку:

pab ( sop( sab (P1,P2), midpoint (P1, P2)), ... ) ≡ pab ( midline (P1, P2, P3), midline (P2, P3, P1) )

Поскольку тождество вида pab ( sop (n, A), …) ≡ B означает, помимо прочего, что точки A и B лежат на общем перпендикуляре к n, можно выразить A следующим образом:

Что можно рассматривать как алгоритм деления любой из сторон треугольника пополам (он более эффективен, чем деление отрезка при помощи угольника [23], если требуется выполнить деление двух или трех сторон).

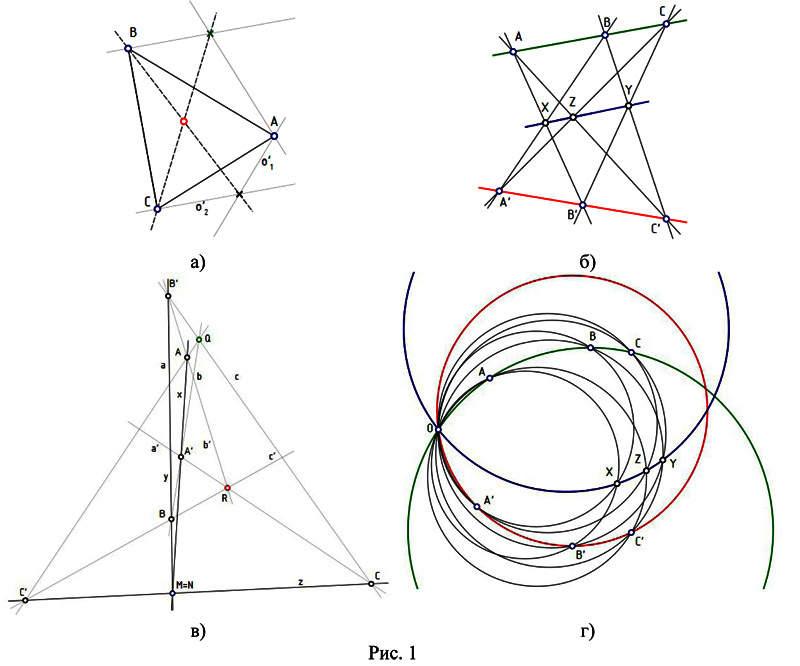
3.2. Принцип двойственности. Рассмотрим построение на основе теоремы Паппа (рис. 1, б):

Поскольку построения sab и pab двойственны, соответствующее составное построение можно получить заменой sab на pab и наоборот, и для наглядности — переменой строчных и заглавных букв в именах объектов (рис. 1, в):

3.3. В.Ф. Каган приводит пример интерпретации евклидовой геометрии [28], в которой в качестве прямой рассматривается окружность, проходящая через некоторую фиксированную точку O на плоскости. В этом случае окружность также однозначно определяется парой точек. Пересечением прямых в этом случае является вторая, кроме O, точка пересечения соответствующих окружностей. На рис. 1, г показаны соответствующие построения. Теорема Паппа справедлива и в этой интерпретации. Построения pab и sab предварительно объявлены следующим образом:

sub sab (A, B)

Элементарные построения c3p и p2c2 строят окружность по трем точкам и вторую точку пересечения окружностей, кроме заданной.

4.

Методическое значение предлагаемого подхода заключается в том, что при изучении некоторых разделов конструктивной геометрии, например, начертательной, методы и алгоритмы можно не только рассматривать, как нечто данное, но последовательным образом получать. Это позволяет, в частности, в обсуждении алгоритмов пользоваться терминами задачи, а не сводить их к элементарным движениям карандаша и циркуля.

Рассмотрим построение некоторых элементов начертательной геометрии. Модель (двухкартинный чертеж) точки по ее координатам формирует следующее построение:

— где hrd и vrd – вспомогательные горизонтальная и вертикальная прямые на заданном расстоянии от указанной точки (O – начало координат на чертеже).

Модель прямой — следующая:

straightab (A, B) = new ( p1 = sab(A.p1, B.p1), p2 = sab(A.p2, B.p2) )

Построение точки на прямой по одной из ее проекций:

Модель плоскости общего положения, заданной прямой и не лежащей на ней точкой, — следующая:

planesp (s, P) = new (P0 = P, s0 = s)

Последнее построение, фактически, ничего не делает, поскольку плоскость общего положения не имеет проекции в виде фигуры.

Другие способы определения плоскости общего положения:

и т. д.

Фронталь плоскости:

Предположим, что плоскость задана, в свою очередь, фронталью (pl.s0) и точкой (pl.P0). Вначале проводится вспомогательная линия h – фронтальная проекция фронтали и пересекается с фронтальной проекцией pl.s0. Они должны пересечься в несобственной точке A. Попытка провести через нее вертикальную линию связи v в pointspr (см. выше) приведет к тому, что v окажется несобственной и проекции построенной таким образом точки A будут несобственными точками проекций pl.s0.p1 и pl.s0.p2, соответственно. Проведенные через них проекции фронтали f будут параллельны проекциям pl.s0, как и должно быть.

При решении более сложных задач задействуются ранее описанные построения, поэтому на каждом этапе алгоритмы сохраняют компактность и осмысленность производимых действий:

Другая возможность связана с непосредственным созданием некоторой системы построений, например, оригами для решения задач.

Заключение

Довольно простой синтаксис рассматриваемого языка предполагает возможность реализации соответствующего транслятора.

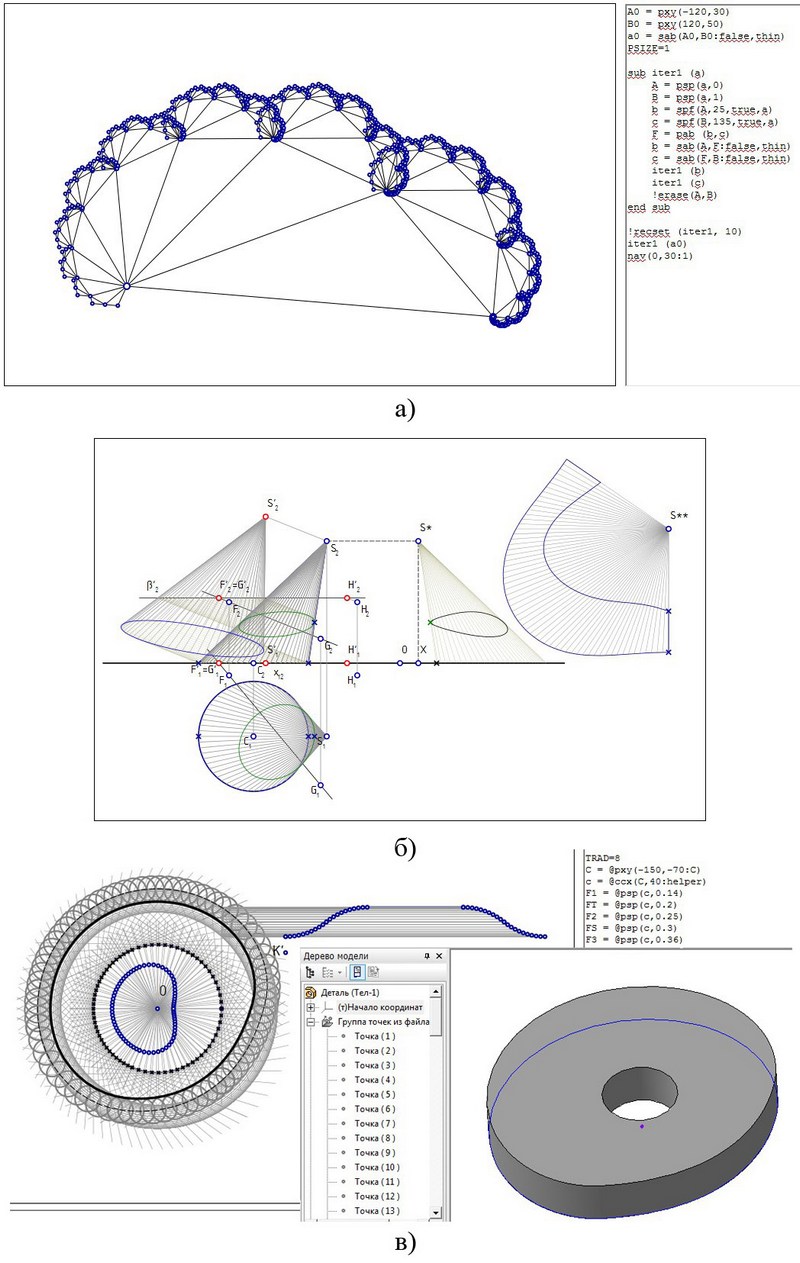
Некоторые из перечисленных компонентов языка были реализованы в составе интерпретатора графических команд. Иллюстрации к настоящей статье были выполнены с его помощью. На рис. 2 показаны примеры работы графических алгоритмов. Такие алгоритмы использовались при проведении лабораторных работ по курсу машинной графики (основные лабораторные работы студенты выполняют в среде C++, используя методы аналитической и вычислительной геометрии) в качестве наглядных примеров альтернативного подхода (на рис. 2, а — фрактальный алгоритм). На рис. 2, г показан учебный пример совместного применения разработанного интерпретатора и системы «Компас», как это было показано в [29] для системы «Симплекс».

Список литературы

1. Бодрашова Г.Ф., Марков В.М., Пугин Г.А. О необходимости унификации обозначений в курсе начертательной геометрии // Сборник науч.-метод. статей по НГ и ИГ. М.: Высшая школа, 1985. Вып. 12. С. 21-25.

2. Гирш А.Г. Символические обозначения в инженерной геометрии // там же. С. 25-28.

3. Маркова А.П. Обучение студентов составлению алгоритмов решения задач инженерной графики // Сборник науч.-метод. статей по НГ и ИГ. М.: Высшая школа, 1976. Вып. 3. С. 8-13.

4. Окунева П.С. Символический язык — материализованная база лексического языка инженерной графики // Там же. С. 70-75

5. Королевич А.И. Об алгоритмизации решения элементарных метрических задач // Прикладная геометрия и инженерная график // Прикладная геометрия и инженерная графика. К., 1965. Вып. 1. С.9-15.

6. Королевич А.И. Об алгоритмизации решения позиционных задач // Прикладная геометрия. Труды первой науч.-метод. конференции по прикл. геометрии и инженерной графике вузов Северного Кавказа. Новочеркасск, 1967. С.90-96.

7. Волков В.Я., Юрков В.Ю. Некоторые вопросы теории и приложения исчислительной геометрии // Геометрические модели и алгоритмы. Л., ЛИСИ, 1989. С.31-36.

8. Волков В.Я. Курс начертательной геометрии на основе геометрического моделирования / В. Я. Волков [и др.]. Омск: СибАДИ, 2010. 254 с.

9. Волков В.Я. Элементы математизации теоретических основ начертательной геометрии / В. Я. Волков [и др.]. // Геометрия и графика. М.: Инфра-М, 2015. Том. 3. Вып. 1. С.3-16.

10. Волошинов В.А. О комбинированных проекционных моделях // Геометрические модели и алгоритмы. Л., ЛИСИ, 1989. С.36-46.

11. Пеклич В.А. Высшая начертательная геометрия. М.: АСВ, 2000. 344 с.

12. Глоговский В.В., Гринева Б. М., Гнатюк М. О. Начертательная геометрия на алгоритмической основе. Львов: Вища школа, 1978. 148 с.

13. Глоговский В.В. Элементарные конструктивные задачи по начертательной геометрии. Львов: Вища школа, 1981. 152 с.

14. Глоговский В.В. Операторы графических отображений (часть 1) // Прикладная геометрия и инженерная графика. К., 1983. Вып. 35. С.126-129.

15. Стародетко Е.А. Элементы вычислительной геометрии. Минск: Наука и техника, 1986. 240 с.

16. Горелик А.Г. Пакет программ машинной графики для ЕС ЭВМ. М., 1986. 320 с.

17. Баяковский Ю.М., Галактионов В.А., Михайлова Т.Н. Графор. Графическое расширение фортрана. М.: Наука, 1985. 288 с.

18. Хейфец А.Л. Геометрически точная 3D анимация кинематических поверхностей. URL: http://dgng.pstu.ru/conf2017/papers/78

19. Гирш А.Г. Задание и построение квадрики [Электронный ресурс]. URL: http://dgng.pstu.ru/conf2017/papers/2/

20. Волошинов Д.В. Конструктивное геометрическое моделирование. Saarbrucken: Lambert Academic Publishing, 2010. 355 с.

21. Волошинов Д.В. ГЕОМЕТРИЧЕСКАЯ ЛАБОРАТОРИЯ. Новый геометрический инструмент. URL: http://dgng.pstu.ru/conf2017/papers/60

22. Волошинов Д.В., Казначеева Е.С., Хайбрахманова Е.С. Автоматизация проектирования поверхностей на основе конструктивных геометрических моделей. URL: http://dgng.pstu.ru/conf2017/papers/117

23. Четверухин Н.Ф. Методы геометрических построений. 1952. 148 с.

24. Адлер А. Теория геометрических построений. Л., Учпедгиз, 1940. 232 с.

25. Рыжов Н.Н. Параметрическая геометрия. М.: МАДИ, 1988. 56 с.

26. Автоматизированное проектирование. Геометрические и графические задачи / В.С. Полозов [и др.]. М.: Машиностроение, 1983. 280 с.

27. Бойков А.А. Автоматизация проверки инженерно-графических заданий [Электронный ресурс]. URL: http://dgng.pstu.ru/conf2016/papers/97/

28. Каган В.Ф. Очерки по геометрии. М., 1963. С. 42-48.

29. Никифоров П.В. Получение кривой теоретического профиля Жуковского для создания 3D-модели поверхности крыла. URL: http://dgng.pstu.ru/conf2017/papers/62/