Исследованы представления о наглядности в начертательной геометрии, компьютерной графике и многомерной геометрии. Показано, что эти представления формируют учебную дисциплину «Наглядная инженерная геометрия» как первую профессиональную дисциплину для бакалавриата технического вуза. В ее основу положены взгляды современной геометрии о наглядном изображении форм геометрических моделей объектов и отношений между ними в электронной версии, а также о неограниченном разнообразии многомерности пространства.
Ключевые слова: геометрия, наглядность, многомерное пространство.
В русском языке слово «наглядность» тесно связано со зрительным восприятием. Практически все теории зрительного восприятия строятся на одном и том же постулате – объективности физической среды внешнего мира. Феноменальный предметный образ восприятия – зрительный перцепт – является результатом превращения в зрительные ощущения энергии электромагнитного излучения светового диапазона, попадающего на сетчатку глаза. При этом в отношениях между средой и перцептом нет взаимооднозначности. Дальнейший этап обработки зрительных сигналов происходит в больших полушариях головного мозга, где не только автоматически анализируется сетчатое изображение, но и дополнительно привлекаются процедуры более высокого когнитивного уровня. Таким образом, физиологи установили, что изображение не отображается в мозге как в фотоаппарате, а конструируется мозгом из сенсорных образов, зрения по правилам и алгоритмам зрительной системы, эволюционно приспособленной для восприятия объемных предметов реального мира.
Стало очевидным, что наша зрительная система приспособлена только для восприятия объемных предметов реального мира, а не для восприятия объектов и фона в виде двумерных плоских поверхностей. Именно эволюция развития зрительного восприятия реального мира, в котором существует человек, сделала трехмерное пространство бытовой формой существования материи, а наше образование и воспитание, отталкиваясь от этого представления, привели лучшие умы человечества к понятию о многомерности мира и его бесконечности. Поэтому все другие виды пространств с размерностью, отличающейся от n=3, т.е. и двумерные, и многомерные, выступают как абстрактные. Когда вместо трехмерного объекта обучающемуся предлагается двумерное изображение, это приводит к возникновению у него психологического барьера при зрительном восприятии, т.к. это изображение не продвигается дальше в мозг для последующей обработки. В этом и заключается абстрактность двумерного изображения, т.е. невозможность непосредственного восстановления объемного изображения в мозге по его двумерной картине. Вместе с тем, в своей жизнедеятельности на всех ее уровнях проявления, человеку приходится иметь дело с двумерными изображениями. В этом случае определяющую роль играет запоминание в памяти, достигаемое за счет непрерывного обучения на всем его протяжении, зависящее от степени и интенсивности этого обучения, навыка, понятности дальнейших логических построений и прямые аналогии в трехмерном пространстве.
В основе представления о реалистической визуализации геометрических моделей лежит понятие о ее наглядности. Понятие «наглядность» связывают не с самими предметами, а с их графическими моделями; при этом существует такая зависимость между предметом и его изображением, которая позволяет по изображениям получать те знания, которые непосредственно или с некоторыми поправками могут быть отнесены к моделируемому объекту. Наглядность модели относительна. С одной стороны, она зависит от свойств самой модели – её материала, размера, цвета, размерности пространства, в котором она построена. С другой стороны, она зависит от жизненного опыта, профессионализма, возраста и личных особенностей познающего человека, т.е. всего того, что называют жизненным опытом, подкрепленным воспитанием и образованием.
Предъявляемые к наглядной модели требования зависят от цели ее создания: это – или художественный образ, или обучение учащихся, или, наконец, создание изображения для последующей материализации объекта, т.е. создание чертежа. При создании художественного образа даже не всегда стремятся получить изображение, равноценное оригинальному. Чем больше недосказанность, тем больше простора для субъективного понимания. Заботой педагога всегда является наглядность изображения-модели. Преподаватель геометрии заинтересован, прежде всего, в наглядных изображениях, практически не заботясь об их обратимости при проецировании на плоскость. Так О.А. Вольберг для преподавателей стреометрии в средней школе разработал специальную теорию построения одного изображения (теорию монопроекций). Проецирование пространственной фигуры на плоскость, хотя и может для некоторых условий дать наглядное изображение, но геометрически оно не равноценно оригиналу. Две проекции одной и той же фигуры позволяют восстановить оригинал, т.е. дают изображение геометрически равноценное оригиналу.
Метод двух ортогональных проекций, разработанный Гаспаром Монжем, нашел широкое применение в технике вплоть до середины ХХ века. Именно Г. Монж, будучи основателем начертательной геометрии, указал на практическую направленность созданной им науки, отметив, что начертательная геометрия является языком, необходимым инженеру для создания чертежей. Эта практическая направленность начертательной геометрии и закрепилась в системе высшего инженерного образования вплоть до настоящего времени. Несмотря на пожелание самого Г. Монжа о совместном изучении начертательной геометрии и аналитического анализа, последний в системе современного высшего образования явился уделом чистой математики.
Необходимость точного измерения изображения-модели по проекциям на плоскости, отодвинула требование наглядности изображения на второй план. Метод Г. Монжа оказался практически лишенным всякой наглядности. Поиск способа повышения наглядности при проецировании на две плоскости проекций при сохранении возможности частичного измерения привел к созданию аксонометрии. Этот метод изображения слагается из метода двух параллельных проекций в сочетании с дополнительным изображением трех взаимно перпендикулярных осей и масштабных единиц на них, позволяющий просто измерять отрезки, параллельные координатным осям. При этом необходимо отличать аксонометрическую систему координат при построении аксонометрических изображений в начертательной геометрии от натуральной системы координат трехмерного пространства. С целью повышения наглядности при создании двух-(трех)-картинных чертежей Г. Монж разработал теорию теней, целиком основанную на всем известном явлении о прямолинейности распространения света. Если направление световых лучей известно, одна проекция с изображением теней дает полное представление о рассматриваемом предмете; в случае двух проекций тени строятся на обеих проекциях, что повышает наглядность по сравнению с построением обеих проекций без теней.
Создание современного персонального компьютера позволило подойти к разрешению проблемы одновременного обеспечения обратимости изображения и его наглядности за счет их раздельного представления в одном техническом приборе. При этом обратимость изображения обеспечивается математическими методами, а наглядность – геометрическим моделированием на основе создания электронной модели.
Создание персональных компьютеров предоставило в руки исследователей широкие возможности по повышению наглядности получаемых геометрических моделей. На экране компьютера наблюдатель, по-прежнему, имеет двумерное изображение, однако многочисленные привлекательные возможности компьютера: вращение и перемещение изображения, разнообразные линейные преобразования, сплайн-аппроксимация, цвет, штриховка, типы линий и т.д. и т.п. позволяют наиболее наглядно имитировать трехмерность изображения-модели при зрительном восприятии её с экрана компьютера. Особо отметим возможность аксонометрии и построения изображения-модели одновременно на нескольких экранах (рис. 1). Поскольку аксонометрия, как известно, это – содержание изображения, а не только способ его получении, аксонометрическое построение на компьютере позволяет наблюдать предмет с разных точек просмотра и не связано с двойным проецированием как при построении на чертеже. Известно, что при зрительном восприятии образа существенное значение имеет движение глаз, что повышает наглядность зрительного восприятия. Одновременное появление изображения-модели при её создании на нескольких экранах с разных точек просмотра заставляет переводить взгляд с одного изображения на другое, что отвечает восприятию объекта в естественных условиях, тем самым повышается наглядность изображения.
При работе на компьютере пользователю компьютерных программ совсем не требуется вникать в устройство используемого оборудования; он должен умело использовать современный инструментарий для решения своих собственных задач. Такими задачами при обучении бакалавров в техническом вузе являются те разделы конструктивной геометрии, которые традиционно представляют интерес для будущих инженеров. Например, если темой изучения является «Пересечение поверхностей», то именно на понятии о порядке линии пересечения поверхностей, условиях образования этих линий и тех частных случаях, когда кривая распадается на несколько линий более низкого порядка (см. рис.1) и следует сосредоточить внимание слушателей и отказаться от морально устаревших способов ручного построения линии пересечения, полезных только при создании чертежа. Эти способы сегодня не актуальны и в присутствии компьютера не найдут практического применения.
Электронная модель изделия становится ключевым понятием в современном наукоемком машиностроении, являясь основным средством проектирования, производства, сопровождения изделия на протяжении всего жизненного цикла [1]. Эта стратегия научного, технического, технологического, экономического развития страны рассчитана на инженерные кадры, подготовленные вузами для решения таких задач. Отсюда очевидно, что в содержании программ при подготовке студентов в техническом вузе электронная модель становится первичным понятием и заменяет собой плоскую модель-изображение, получаемую при проецировании на две плоскости проекций.
Как было отмечено выше, только для трехмерной модели мозг человека может создать ее зрительный образ по её зрительному восприятию. Поэтому все другие пространства с размерностью, отличающейся от n=3, являются для человека абстрактными.
Творцом геометрии n-мерного пространства считают Грассмана, который ввел в рассуждение неопределенное число n координат точки Х1, Х2, …Хn вместо трех координат X, Y, Z. Аналитический подход к n-мерной геометрии очень прост и удобен для многих приложений. Преимущество такого способа описания фактов заключается в том, что он подчеркивает некоторые обстоятельства алгебраического характера, которые не зависят от числа измерений n и, вместе с тем, в случае n≤ 3 могут быть наглядно интерпретированы.
Вместо формального обобщения обычной аналитической геометрии на произвольное число измерений, Шлефли было предложено чисто геометрическое изложение n-мерной геометрии, не зависящее от аналитического аппарата.
Под пространством в современной геометрии понимают вообще любую совокупность однородных объектов (явлений, функций, фигур, значений переменных и т.п.), между которыми имеются отношения, подобные обычным пространственным отношениям (непрерывность, расстояние и т.д.). Эти отношения определяют то, что можно назвать строением или «геометрией» пространства. Сами объекты играют роль «точек» такого пространства; «фигуры» – это множество его «точек». Разнообразию возможностей совокупности объектов и различных отношений между ними отвечает неограниченное разнообразие пространств, изучаемых в науке, например, даже семантическое пространство в экспериментальной психологии.
Примерами, на которых можно наглядно увидеть существенную разницу между пространствами разных измерений служит геометрия многогранников, где рассматривается «пространство» тех или иных фигур. По рис. 2 можно наглядно наблюдать, как существенно изменяется геометрия такой фигуры как симплекс (простейший правильный тетраэдр) при последовательном изменении размерности его пространства от n = 0 до n = 4. Последовательное добавление одной точки, не лежащей в одной плоскости с рассматриваемой фигурой, позволяет «переводить» фигуру в новое измерение. Аналогию можно продолжить и далее, выйдя за пределы трехмерного пространства, т.е. для размерности n = 4. Теперь уже наглядно выявилась геометрия четырехмерного правильного многогранника, так называемого четырехмерного симплекса (см. рис. 2а). Это есть не что как пирамида с тетраэдром в основании. Если повторить такой же прием для любого числа измерений n, получим простейший n-мерный многогранник, так называемый n-мерный симплекс. Из построения можно определить, что он имеет n+1 вершину. Можно убедиться, что все его грани суть симплексы меньшего числа измерений: (n–1)-мерные, (n–2)-мерные и т.д. Представленная наглядная геометрия позволяет вывести математическое понятие об абстрактном n-мерном декартовом пространстве, которое обозначается как Rn. Число n называется размерностью пространства или числом измерений. Таким образом, со структурной или комбинаторной точки зрения простейшими геометрическими фигурами размерностей 0, 1, 2, 3, 4 являются соответственно точка (R0), отрезок (R1), треугольник (R2), тетраэдр (R3), четырехмерный симплекс (R4).
Из существования пространства многогранников и пространства их разверток установлено, что в многомерном пространстве существует соответствие между точками этих пространств. На рис.2,б приведены примеры разверток соответствующих правильных многогранников. Поскольку размерность развертки, являющейся по определению поверхностью многогранника, на единицу меньше, чем размерность самого многогранника, развертку четырехмерного симплекса можно непосредственно построить на компьютере, совместив её соответствующим образом с его трехмерным пространством.
Некоторые представления о многомерной геометрии правильных многогранников были апробированы в научно-исследовательских работах со студентами младших курсов МГТУ им. Н.Э. Баумана в рамках СНТО. Были построены на компьютере 3D-электронные модели разверток правильных четырехмерных симплекса, куба и 16-гранника (многогранник типа октаэдра). По построенным электронным моделям были напечатаны на 3D принтере их материальные образы, фотографии которых представлены на рис.3.
Существует реальный физический смысл абстрактного понятия многомерного пространства. Оно отражает действительность и было вызвано потребностями науки, а не праздной игрой воображения. Именно такую мысль, по мнению А.Д. Александрова, и следует донести до студентов при их обучении наглядной многомерной геометрии. Так, если мы имеем сложную физическую систему, состояние которой задается не двумя, а например, пятью данными, то графическое изображение ее поведения приводит к представлению соответственно о пятимерном пространстве, где каждая точка задается пятью координатами, соответствующими пяти данным состояниям системы. Пример из области геометрии: шар задается четырьмя данными – тремя координатами его центра и радиусом. Поэтому шар можно представить точкой в четырехмерном пространстве. Такие представления находят применение в физической химии и материаловедении на основе понятия фазового пространства системы; в машиностроении при обработке материалов на многокоординатных станках с ЧПУ; при контроле изделий на многокоординатных контрольно-измерительных машинах, 3D сканерах и т.д. Так, общий принцип действия координатно-измерительных машин состоит в сканировании объекта по точкам щупом. Координаты точек, определенных измерительным наконечником, затем передаются в компьютер для анализа. Эта процедура, называемая «математическим выравниванием» позволяет не использовать физические носители форм и размеров. Из всего сказанного выясняется общее реальное основание для введения понятия многомерного пространства. Если какая-либо фигура или состояние какой-либо системы задаются n-данными, то эту фигуру, это состояние можно представить как точку некоторого n-мерного пространства .
В профессиональную компетенцию инженера с политехническим образованием должны входить современные представления о многомерности пространства в самом широком смысле этого понятия. Такое представление современный студент может получить на начальной стадии своего профессионального обучения в рамках компетенции такой учебной дисциплины как «Наглядная инженерная геометрия» [2, 3]. Эта первая профессионально ориентированная общеобразовательная дисциплина построена на современных информационных технологиях и использовании современного инструментария – компьютера, 3D принтера и 3D сканера. Время только подтвердило ранее высказанную мысль [4] о том, что в системе высшего технического образования нельзя полностью отказаться от предметного принципа разделения содержания образования, поскольку такое разделение объективно отражает структуру научного знания.
Список литературы
- Международная энциклопедия CALS-технологий. Авиационно-космическое машиностроение. Гл. редактор Братухин А.Г. – ОАО «Научно-исследовательский центр автоматизированных систем конструирования», 2015, 608 с.
- Соколова Л.С. Наглядная инженерная геометрия в техническом университете // Высшее образование сегодня. –М., 2016, №12, с.41-43.
- Соколова Л.С. Геометрическая подготовка бакалавров в современных условиях// Труды КГП – 2016, Пермь, 2016, вып. 3, с.326-332.
URL: http://dgng.pstu.ru/conf2016/neus/35/ - Е.В. Караваева, В.А. Богословский, Д.В. Харитонов. Принципы оценивания уровня освоения компетенций по образовательным программам ФГОС нового поколения// Вестник Челябинского государственного университета, 2009; № 18, вып.12, с.155-162.
Рисунки к докладу
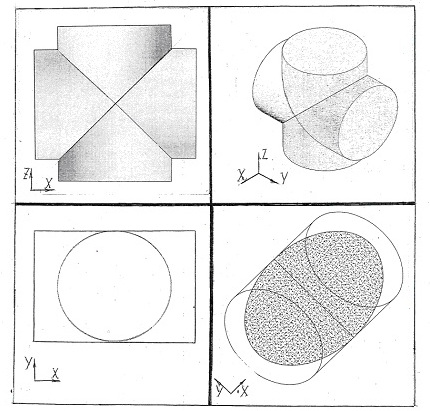
Рис. 1
Распадение линии пересечения двух цилиндров, описанных около сферы
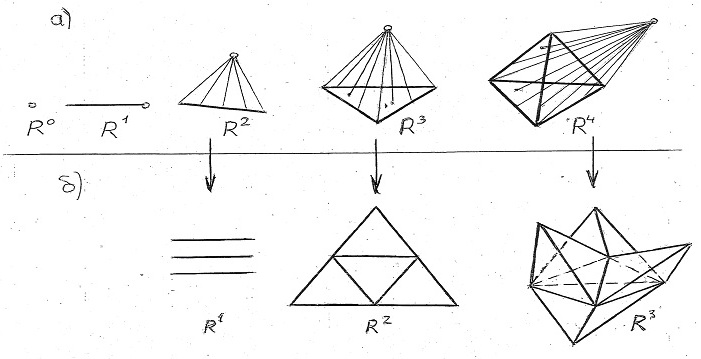
Рис. 2

Рис. 3
Прототипирование на 3D принтере разверток правильных четырехмерных многогранников: симплекса (из 5 тетраэдров), куба (из 8 кубов), 16-гранника (из 16 тетраэдров); слева - направо
Вопросы и комментарии к выступлению:

Тихонов-Бугров Дмитрий Евгеньевич (5 марта 2017 г. 21:17) |
Людмила Сергеевна, здравствуйте. Спасибо за интересный доклад. Изучается ли в Вашем вузе "Наглядная инженерная геометрия" как полноправная дисциплина или это некая заготовка? Если да, то интересно узнать: кафедра; объём; место в учебном процессе; смежные дисциплины. С уважением, Тихонов-Бугров. |

Селиверстов Александр Владиславович (6 марта 2017 г. 2:53) |
Не дай мне Бог сойти с ума. Нет, легче посох и сума... (А.С. Пушкин) Уважаемая Людмила Сергеевна! Не могу найти слов, чтобы комментировать большую часть Вашего доклада. Но некоторые вопросы хотелось бы задать. "Под пространством в современной геометрии понимают вообще любую совокупность однородных объектов..., между которыми имеются отношения, подобные обычным пространственным отношениям (непрерывность, расстояние и т.д.)." "апробированы в научно-исследовательских работах со студентами младших курсов МГТУ им. Н.Э. Баумана" PS Тому, кто хотел бы в увлекательной форме познакомиться с четырёхмерной геометрией, рекомедую почитать роман Эдвина Э. Эбботта "Флатландия", который вышел в 1884 году, а на русском в 1976. Это намного интереснее! |

Головнин Алексей Алексеевич (6 марта 2017 г. 12:20) |
Здравствуйте Людмила Сергеевна! Всегда с большим интересом изучаю Ваши доклады. Еще большее впечатление осталось от Вашего выступления на одной из конференций в МИИТХТ. Они заставляют думать.
Простые детали могут быть описаны словами, значками и цифрами прямо в спецификации, например прокладка – два диаметра и толщина. В 90-м году были методические указания для заочников, когда надо было начертить форму описанную словами, например призма с размерами, в ней выполнено треугольное отверстие и т.д. И все понятно без чертежа. Представляется, что только словами можно описать любую форму, но на каком-то этапе это становится нерациональным. Надо будет написать несколько томов для того, чтобы описать форму. Есть разумная граница, когда вступает в дело чертеж. Он упрощает понимание формы человеком в соответствие с его возможностями. Ведь и Монж придумал НГ для упрощения понимания и решения задач.
Нам известно, что у многомерности есть применение в ядерной физике, куда мы можем заглянуть только при помощи игры ума, но многомерность в представленном виде, не может служить предметом науки и преподавания. Еще, лет 30-40 назад слушал лекции профессора Тарасьева по тензорному анализу. Он, в частности, рассказывал, что оппонент в качестве большого преимущества его диссертации (по многомерности, насколько я понял) назвал отсутствие в ней иллюстраций (читай наглядности). С уважением Головнин А.А. |

Шахова Алевтина Бруновна (6 марта 2017 г. 12:54) |
Здравствуйте Людмила Сергеевна, с интересом ознакомилась с Вашим выступлением, вопросы, которые у меня появились уже заданы нашими коллегами. Обратилась к материалам пршолой КГП-2016, где Вы уже начали развивать данную тему, всвязи с этим хотелось бы уточнить ,все это в рамках кафедры "Начертательная геометрия инженерная и компьютерная графика" или нет? Если да ,то каким образом название дисциплины "Наглядная инженерная геометрия" увязывается с ФГОСами и лимитом дисциплины. Доклад интересен, актуален ---это научная работа или попытка изменить мышление коллег? С уважением Шахова А.Б. |
|
Минеев Алексей Борисович (9 марта 2017 г. 17:08) |
Уважаемая,Людмила Сергеевна! К сожалению термин наглядная многомерная геометрия не имеет смысла.Т.к. человек не может представить и изобразить различными средствами многомерность пространства.В существующих ныне теориях есть 10-мерное,26-мерное ,п-мерное пространства.Но все это пока умозаключения ученых,чистая теория.Будь иначе,мы бы давно перемещались в пространстве-времени между Вселенными без особых проблем. |
|
Соколова Людмила Сергеевна (9 марта 2017 г. 20:51) |
Уважаемый Алексей Алексеевич! |
|
Соколова Людмила Сергеевна (9 марта 2017 г. 21:28) |
С изумлением поняла, что мы, оказывается, лично знакомы через приснопамятную не столько для меня, сколько для присутствующих на ней конференцию в МИИТХТ, которая обратила Ваше внимание на мои взгляды. Спасибо. Конечно, Вы правы, если не нужна наглядность, то можно обойтись и без нее. Но для этого нужен опыт и практика. Я своим студентам сначала объясняю, что прокладкой в технике называется цилиндр, у которого... и т.д. Я обратила внимание, что, когда Вы говорите, "Что есть разумная граница, когда вступает в дело чертеж", почему Вы не сказали "модель"? Это на мой взгляд для Вас было бы более естественно. Перечитываю Монжа и все больше убеждаюсь, что первичным желанием Монжа было создать язык чертежа. И никак не могу согласиться, что Монж придумал НГ для упрощения понимания и решения задач. Понимание наступает только через длительную работу на уровне банального запоминания. Вы же наверное, читаете лекции по НГ? Что касается разверток. Мы имеем дело действительно с развертками, а совсем не с проекциями. Для пояснения напомню, как строится развертка, например, тетраэдра. Поверхность тетраэдра, в целом двумерна, то есть имеет размерность на единицу меньше, чем сам объект. Но эта двумерная поверхность находится в трехмерном пространстве. Разместить её в двумерном пространстве, т.е. в плоскости, не подвергая никаким изменения невозможно. Однако, если на поверхности тетраэдра сделать несколько подходящих разрезов по ребрам, то её можно будет "разогнуть" и уложить в плоскости, т.е. поместить в двумерное пространство. При этом, конечно, будут нарушены все естественные связи между отдельными участками поверхности и будут изменены все углы между соседними не отрезанными друг от друга гранями. В результате поверхность тетраэдра превратится в кусок плоскости, который и называется разверткой тетраэдра. Как видите, это совсем не проекции. Математики по такому-же принципу разработали теорию создания разверток n-мерного пространства. При создании модели разверток четырехмерных тетраэдра, куба и октаэдра мы использовали эту теорию, строя электронные модели и затем прототипируя их. Кстати, о прототипировании, мною двигал чисто наглядный интерес и возможность показать как выглядит материальный объект никому неизвестных до этих пор разверток четырехмерных фигур и продемонстрировать возможность использования современного инструментария в нашей области. У современного молодого человека понятие многомерного пространства вызывает неподдельный интерес. Представляя тему разверток четырехмерных правильных симплексов на Бауманской конференции "Политехника" 7-10 октября 2016 г. студенты сделали такую презентацию материала, что привлекли внимание к стенду не только своими результатами, но и заинтересованными рассказами о четырехмерном физическом пространстве. Именно возможность понимания многомерного пространства вызвала у молодежи неподдельный интерес. |
|
Соколова Людмила Сергеевна (10 марта 2017 г. 18:45) |
Здравствуйте Дмитрий Евгеньевич! Извините, что так задержалась с ответом на Ваш вопрос. Наглядная инженерная геометрия существует сегодня как Проект Программы С уважением Л.С. Соколова |
|
Соколова Людмила Сергеевна (10 марта 2017 г. 18:46) |
Здравствуйте Александр Владимирович! Сходу и от неожиданности не смогу ответить Вам достойным эпиграфом из художественной прозы. Проза же жизни такова. Предлагается пропедевтический курс наглядной многомерной геометрии на уровне знакомства с её понятиями о существовании разных пространств. Критикуемое Вами определение пространства дано не мною, а целиком цитируется (слово в слово) из статьи А.Д. Александрова «Абстрактные пространства» в книге «Математика, её содержание, методы и значения». Том третий, изд. Академии наук СССР, Москва, 1956, глава XVII, с.151, абзац второй сверху. Совершенно не понятен Ваш гнев по поводу апробирования построения разверток четырехмерных симплекса, куба и 16-гранника по их электронным моделям и их прототипирование на 3D принтере с целью получения материальных объектов. Наша кафедра «Инженерная графика» как и любые другие подразделения университета ведет в рамках студенческих СНТО научно-исследовательские работы по тематике, представляющей интерес для кафедры. Работа со студентами младших курсов в рамках их знакомства с многомерной геометрией продолжалась два года. Результаты работы студенты публиковали в Молодежном научно-техническом вестнике МГТУ им. Баумана за 2015-2016 гг. и представили их на Всероссийском конкурсе научно-исследовательских работ проводимом в рамках форума «Политехника». Работа отмечена дипломом второй степени в номинации «Инженерная и компьютерная графика в промышленных задачах». Представленные на рис.3 фотографии – результат их работы. Студенты успешно учатся на своих кафедрах по выбранным ими специальностям, приобретя опыт научно-исследовательской работы и набрав конкурсные баллы для продолжения учебы в магистратуре. Что же касается Вашего ёрничения по поводу функционирования «зрительная система – мозг», то это опять не мои провокации, а результаты исследования психофизиологов. С уважением Л.С. Соколова |
|
Соколова Людмила Сергеевна (10 марта 2017 г. 18:47) |
Уважаемая Алевтина Бруновна, здравствуйте! Наглядная инженерная геометрия рассматривается мною как профессионально ориентированная общеобразовательная дисциплина для кафедр «Инженерная графика» технических вузов при подготовке бакалавров. Эти кафедры создавались специально под обучение будущих инженеров умению составить и прочитать чертеж. Теоретическая основа базировалась на НГ. В современных условиях перехода на инновационные технологии в производстве на смену чертежу пришла (за рубежом уже, а в России идет) электронная модель изделия. В таких условиях кафедры инженерной графики с классическими программами идут в разрез со временем и теряют свое предназначение, а надежды на технологии трехмерного моделирования просто толкают их в объятия кафедр информационных технологий. На мой взгляд, кафедры инженерной графики могут себя сохранить, если только предъявят спецкафедрам новое видение начальной подготовки студентов на младших курсах, вкладывая этим самым свою долю в формирование профессиональной компетенции инженера, которая, надо признать, в основном, создается выпускающими кафедрами. Задачи, возлагаемые на кафедры инженерной графики как самостоятельных единиц в составе технического вуза, должны в рамках общих результатов убедить спецкафедры в необходимости и современном уровне решаемых ими задач. Так через общий результат произойдет увязка с требованиями ФГОСов. Если кафедры инженерной графики по-прежнему будут предлагать НГ и пытаться научить работать с чертежом они потеряют интерес для спецкафедр, что приведет к отказу от сотрудничества. Это, надо признаться уже назревает. В Самарском аэрокосмическом университете ректор запретил учить студентов, используя эскизы и чертежи: только электронные модели изделий (см. КГП-2016). Предлагаемая программа «Наглядная инженерная геометрия» является альтернативой для действующей учебной программы, а трибуной для неё являются только конференция КГП и научные публикации. С уважением Л.С. Соколова |
|
Соколова Людмила Сергеевна (10 марта 2017 г. 18:50) |
Здравствуйте, Алексей Борисович! Существуют два подхода к изучению геометрии: аналитический и наглядный. Пример использования аналитического анализа Вы можете увидеть в статье Г.С. Иванова и И.М. Дмитриевой, представленной на этой конференции. Наглядный подход я попыталась продемонстрировать через рис.2 и текст к нему, а также через создание разверток правильных четырехмерных симплексов. Наглядность – это не только возможность непосредственного созерцания, но и достижение понимания решаемой задачи. С уважением Л.С. Соколова |

Селиверстов Александр Владиславович (10 марта 2017 г. 22:38) |
Здравствуйте, Людмила Сергеевна! |

Головнин Алексей Алексеевич (10 марта 2017 г. 23:51) |
Здравствуйте Людмила Сергеевна! Ваш ответ уважаемой Алевтине Бруновне выглядит как убедительное обоснование необходимости смещения акцента в учебном процессе наших кафедр от чертежа в сторону ЭМИ. В этом я Ваш единомышленник, еще несколько докладов и выступлений, как я понимаю, свидетельствуют об уже происходящих изменениях. Однако не понятно, почему Вы альтернативную программу связываете с наглядностью. Если в чертеже вопрос наглядности (понятности) очень важен, мы учим студентов выбирать количество изображений, главный вид, масштаб и т.п., то в ЭМИ вопрос о наглядности, как нам представляется, вообще не стоит. В жизни мы не говорим о наглядности, а просто смотрим на объект, также и на ЭМИ, повторяющую форму и размеры оригинала, достаточно просто смотреть. Не увязывают, насколько мы понимаем, прогресс в конструкторском документировании с акцентом на наглядность и за рубежом, о котором Вы напоминаете. Избранное Вами направление очень отличается от других вариантов корректирования графо-геометрической подготовки, представленных, например, на этой конференции. И привязка к наглядности многомерности, не говоря о правильности ее использования, выглядит притянутой. Разделяя поздравления уважаемого Александра Владиславовича по поводу победы Ваших студентов на конкурсах, все же считаем, что увлечение многомерностью наносит вред их образованию. Понятно, что это лучше, чем ничего, но тем не менее. С уважением Головнин А.А. |

Шахова Алевтина Бруновна (11 марта 2017 г. 11:50) |
Уважаемая Людмила Сергеевна, спасибо за столь развернутый ответ, все о чем вы пишете, реализовано и реализуется на нашей кафедре уже в течении лет 15-17лет, о чем мы бесконечно пишем и говорим и на страницах нынешней КГП и предыдущих, к сожалению столь активное участие ваших коллег(бауманцев) и Вас началось только в этом году. А мой вопрос о названии дисциплины состоит в том, можно и не интерпретировать а данные методы преподавания использовать в рамках нашей дисциплины, которая имеет четкую формулировку, "Начертательная геометрия инженерная и компьютерная графика". Ведь речь идет об инструменте восприятия и название дисциплины вполне это не только допускает, но и обуславливает. А об уровне и подходах на Вашей кафедре очень информативно написала Наталья Евгеньевна. И еще я не согласна с тем, что компетенции формируются только выпускающими кафедрами, и нами тоже. Знаю, что процентов 50-70 студентов, прошедших нашу кафедру моделировать и ЭМД и ЭМИ умеют. С уважением Шахова А.Б. |

Селиверстов Александр Владиславович (11 марта 2017 г. 12:36) |
Здравствуйте, Алевтина Бруновна! С уважением, А.В. Селиверстов |
|
Никифоров Петр Владимирович (13 марта 2017 г. 0:05) |
Цитата "Тому, кто хотел бы в увлекательной форме познакомиться с четырёхмерной геометрией, рекомедую почитать роман Эдвина Э. Эбботта "Флатландия", который вышел в 1884 году, а на русском в 1976. Это намного интереснее!" Существуют более современные формы изложения :), всем рекомендую замечательный фильм "Понять четвёртое измерение", наглядность там просто завораживает. https://www.youtube.com/watch?v=PTsP9RVGFUw А студентам, просмотр - обязателен! |

Головнин Алексей Алексеевич (13 марта 2017 г. 0:50) |
Здравствуйте Петр Владимирович! Приведенная Вами ссылка приводит к ролику в ютубе, который называется «Понять четвёртое измерение просто 1 часть», но в его начале написано настоящее название «la dimension deux», которое переводится как «пространство двух». Французского не знаю, перевод автоматический. По содержанию, на наш взгляд, больше похоже на иллюстрацию темы «Однородные координаты». С уважением Головнин А.А. |
|
Никифоров Петр Владимирович (13 марта 2017 г. 2:29) |
Пусть название роликов останется на совести тех кто их разместил. Всего частей 9, самое интересное - проекции правильных четырехмерных многогранников в трехмерное пространство, начинается с третьей. Прошу прощения что не дал ссылку на все части сразу https://www.youtube.com/playlist?list=PLspHe9GIAIEcLfztmzwfFwB13eMKGxh1f |

Головнин Алексей Алексеевич (13 марта 2017 г. 11:40) |
На совести тех, кто разместивших ролики, наверное, не только название. Те же ролики, совсем под другим названием (Размерность, что меняет суть дела) размещены по адресу. http://www.dimensions-math.org/Dim_tour_RU.htm Там же есть сведения и об авторских правах. Впрочем благодаря приведенной ссылке получилось выйти на очень интересные оригиналы. Картинки из 3-го фильма очень похожи на изгибаемые многогранники, имеющие область применение и перспективу ее расширения: «За решение фундаментальных задач теории изгибаемых многогранников, создающее основы для развития робототехники, отмечен ведущий научный сотрудник Математического института имени Стеклова РАН Александр Гайфуллин.» Подробнее: http://www.newsru.com/russia/08feb2017/future.html С уважением Головнин А.А. |
|
Соколова Людмила Сергеевна (13 марта 2017 г. 18:21) |
Уважаемый, Александр Владиславович! Извините, пожалуйста, за ошибку, допущенную мною в Вашем отчестве. Сведения о психофизиологии зрения заимствованы мною не из популярной литературы, а в результате общения с сотрудниками каф."Психофизиология" МГУ им.М.В.Ломоносова, для которых эти вопросы являются результатами их научной работы. Все предоставленные на этой конференции доклады от МГТУ им. Баумана написаны сотрудниками одной кафедры «Инженерная графика», которыми мы являемся. И взгляды друг друга мы знаем. Поразительно, как легко Вы делаете суждения, за которые Вам, по-видимому, приходится потом извиняться. Развертки 4-мерных правильных симплексов созданы нами совсем не для развлечения .Правильные многогранники многомерного пространства олицетворяют собой подход геометрического изложения п-мерной геометрии, не зависящий от аналитического аппарата. Впервые это было сделано швейцарским математиком Шлефли и в настоящее время уже полностью принято современными математиками ( А Вы,математик?) . Мы использовали этот подход ( см.рис2 и пояснения в тексте). А поскольку этот материал является разделом в предлагаемой учебной программе, то для получения наглядного представления студентами о предмете изучения, мы дополнили его построением разверток 4-мерных симплексов , ибо на компьютере можно построить их электронные модели, а на 3Dпринтере напечатать их материальные образы. В таком виде это сделано впервые и представляет собой новаторский подход. Фотографии представлены на рис.3. Обращаю Ваше внимание, что речь идет о пропедевтическом курсе многомерной геометрии. К сожалению, Вы, Александр Владиславович, оказались плохим стрелком: четыре грубых промаха из четырех попыток. Результат крайне слабый для продолжения общения. Досвидание. Л.С.Соколова |

Рукавишников Виктор Алексеевич (23 марта 2017 г. 14:11) |
Добрый день, Людмила Сергеевна! Последняя надежда на Вас! Может Вы скажите, что это за учебная дисциплина "Инженерная геометрия". Это общенаучная дисциплина? Судя по названию ее методологической основой является наука геометрия. Что является целью и предметом изучения этой дисциплины? Элементом какой системы подготовки является эта дисциплина. Какую компетенцию или ее уровень с помощью ее формируют. Помогите, пожалуйста, понять! К сожалению, другие авторы хранят молчание .... Спасибо, с уважением В.А. Рукавишников |
|
Соколова Людмила Сергеевна (24 марта 2017 г. 21:36) |
Уважаемый, Виктор Алексеевич! Я могу ответить только за ту дисциплину, которую я назвала "Наглядная инженерная геометрия" Пока я буду готовить обстоятельный ответ на Ваши сверхсерьезные вопросы, посмотрите, пожалуиста, мой ответ Алевтине Борисовне Шаховой - он помещен здесь же, всего лишь несколькими разделами выше. Может быть он разъяснит, хотя бы частично, мою позицию по поводу судьбы кафедр инженерной графики в условиях реализации стратегии развития страны в современном наукоемком машиностроении. С уважением.Л.С.Соколова |
|
Соколова Людмила Сергеевна (26 марта 2017 г. 19:53) |
Уважаемый Виктор Алексеевич! Я могу ответить только за ту дисциплину, которую я назвала «Наглядная инженерная геометрия». Создание компьютера привело к смене парадигмы в промышленности – переход от плоской геометрической модели – чертежа – к объемной 3D электронной модели – единой математической мастер-модели. В эпицентре связанных с этим событий оказались кафедры графики высших технических учебных заведений. Эти кафедры создавались специально под обучение будущих инженеров умению составить и прочитать чертеж. Теоретическая основа базировалась на НГ. Оставаясь в рамках устаревших классических программ, наши кафедры идут в разрез не только со временем, но и теряют междисциплинарные связи со спецкафедрами. Последние не видят пользы от сотрудничества и отказываются от услуг кафедр инженерной графики в свою пользу с части учебных часов. Сейчас типовая картина начального обучения компьютерной графике построена по схеме: чертеж→модель→ассоциативный чертеж. Попробуйте догадаться, какие структуры в этой схеме являются лишними, но зато требуют огромных затрат времени и труда. Любая из спецкафедр за 2 занятия познакомит своих студентов с нужным для нее пакетом программ и сразу приступит к дальнейшему обучению по нужным для нее технологиям и на специфических для нее деталях. А нам нужно для этой работы целый семестр с каким-либо одним универсальным пакетом программ и с использованием классических, часто примитивных примеров. В части посягательств на приоритет в геометрическом моделировании мы просто не конкурентно способны перед спецкафедрами. На мой взгляд, кафедры инженерной графики могут себя сохранить, если только предъявят спецкафедрам новое видение начальной подготовки студентов на младших курсах, вкладывая этим свою долю в формирование профессиональной компетенции инженера, которая, надо признать, в основном создается выпускающими кафедрами. Так, через общий результат происходит увязка с требованиями ФГОСов. Такое новое видение начальной подготовки я связываю с геометрической подготовкой будущих инженеров по дисциплине, которая была сформулирована, как «Наглядная инженерная геометрия». Собственно инженерная геометрия входит в составе с компьютерной графикой в номенклатуру научных специальностей ВАК 05.01.01. Таким образом, методологической основой остается геометрия как научное направление деятельности кафедр инженерной графики. Существует профессиональное мнение, что в системе высшего технического образования нельзя полностью отказаться от предметного принципа разделения содержания образования, поскольку такое разделение объективно отражает структуру научного знания. Наглядная инженерная геометрия, оставляя для высшей математики аналитические методы исследования, излагает взгляды современной геометрии о наглядном изображении форм геометрических моделей объектов и отношений между ними в электронной версии, а также дает современном молодому человеку с высшим образованием современные представления о многомерности пространства в самом широком смысле этого понятия. Эти представления, в самом неожиданном, казалось бы фокусе, находят применение в наукоемком производстве. Не поверите, но в ответ на публикацию Проекта программы «Наглядной инженерной геометрии» Инженерном электронном журнале, я по электронной почте 1,5 года назад получила предложение от руководителей технологической службы Тульскогозавода прочитать пропедевтический курс многомерной геометрии для инженеров и наладчиков многокоординатных станков и многокоординатных измерительных машин. Да, не всем бакалаврам в будущем суждено быть руководителями, но им предстоит работать с высокотехнологичным оборудованием и решать на нем серьезные задачи. Но и в медицине, например, на наукоемком оборудовании работают и обслуживают его совсем не санитарки, а люди с высшим образованием и даже кандидаты наук. Бакалавры выйдут из вуза с теми знаниями, которые именно мы им и дадим. И в заключение, отвечая на прямой вопрос Владимира Алексеевича о статусе Инженерной геометрии, формулирую учебную дисциплину «Наглядная инженерная геометрия» следующим образом: Это первая профессионально ориентированная общеобразовательная дисциплина, построенная с использованием современных информационных технологий и современного инструментария. В профессиональную компетенцию инженера с политехническим образованием должны входить современные представления о многомерности пространств в самом широком смысле этого понятия. Эти компетенции он может получить на начальной стадии своего профессионального обучения в рамках такой учебной дисциплины как «Наглядная инженерная геометрия». Спасибо всем, кто дочитал этот материал до конца. С огромным уважением ко всем коллегам Л.С. Соколова |
Назад Go Back