ГЕОМЕТРИЧЕСКИ ТОЧНАЯ 3D АНИМАЦИЯ КИНЕМАТИЧЕСКИХ ПОВЕРХНОСТЕЙ

(Южно-уральский государственный университет (Национальный Исследовательский Университет))

Аннотация

Рассмотрена методика создания анимационных файлов кинематических моделей в пакете AutoCAD. Каждый кадр анимации является результатом геометрически точного расчета, выполняемого с применением программирования на языке AutoLisp. Приведены алгоритмы построения реалистичных 3d моделей линейчатых кинематических поверхностей. Приведен презентационный файл из шести анимаций указанных моделей. Работа предназначена для учебного процесса кафедр графики.

Ключевые слова: линейчатые поверхности, 3d моделирование, геометрические алгоритмы, анимация, программирование, AutoCAD, AutoLisp.

Введение

При изучении и исследовании кинематических моделей существенную помощь оказывает анимация – то есть воспроизведение и демонстрация модели в процессе ее формирования или изменения.

Автор активно применяет анимацию. Для студентов-строителей, архитекторов и дизайнеров применяется анимация в пакете 3dStudioMax: “облететь” вокруг проектируемого здания, осмотреть комнату, квартиру. Такие же задания выполняют студенты в пакете Revit и AutoCAD. В задании по расчету инсоляции студентам требуется показать движение солнечной тени по площадке и стенам зданий микрорайона. Построение анимацией студенты выполняют в рамках контрольных заданий по специальным курсам компьютерной графики.

Можно выделить два типа анимаций. Для первого типа характерно постоянство геометрической формы модели. Такие анимации получают перемещением камеры и (или) ее точки прицела по заданной траектории. Примеры приведены выше. Построение этих анимаций является штатной операцией пакетов САПР и не вызывает трудностей.

Значительно более сложной является задача создания анимации, демонстрирующей формирование или изменение формы геометрической модели. В учебном процессе примером явились анимации формирования сложных кинематических поверхностей, изучаемых в курсе начертательной геометрии, работа зубчатых зацеплений в курсе инженерной графики.

Цель работы: изложение методики создания анимационных файлов в пакете AutoCAD на примере кинематических поверхностей, а также геометрических алгоритмов построения этих поверхностей.

Построения 3d моделей выполнялись в пакете AutoCAD. Язык программирования – AutoLisp.

1. Программирование как основа построения анимации

Анимационный файл создается объединением отдельных растровых файлов – кадров съемки. Для плавного изменения формы модели при длительности фильма в ≈10 секунд желательно создать 150-200 кадров с геометрически точным преобразованием модели между кадрами. Это возможно лишь на основе программного формирования модели и кадров съемки.

Среди общедоступных пакетов САПР (это AutoCAD, SolidWorks, Компас) программирование развито лишь в пакете AutoCAD. В остальных – программирование имеется, но недоступно пользователям. Практически отсутствует литература по программированию в этих пакетах. Напротив, в AutoCAD программирование возможно на трех языках: AutoLisp, Basic и C++. Все они поставляются вместе с пакетом. Из них наиболее доступен AutoLisp. По AutoLisp'у имеется обширная литература [1,2]. AutoLisp позволяет выполнять необходимые аналитические и, что особенно важно, геометрические вычисления, строить геометрические модели из линий, тел и поверхностей, реализовать диалог с пользователем по вводу данных и т.д.

Программа создания анимации должна решать следующие задачи.

1. Управление геометрией модели в соответствии с ее алгоритмом формирования и перестроения согласно сюжету фильма.

2. Управление видом, сохраняемым в кадре. Направление съемки может быть неподвижным, или в процессе съемки изменяться.

3. Для наглядности применяются источники света, благодаря которым динамика процесса подчеркивается движением тени объекта. Положение и параметры источников света могут быть постоянными, либо управляемыми программой.

4. Автоматическое сохранение кадров анимации как растровых файлов. В зависимости от назначения и выделяемых на создание анимации затрат времени для создания растровых файлов могут быть применены различные средства визуализации. Объединение кадров в единый файл выполняется, как правило, внешними общедоступными программами.

Геометрические модели, подлежащие анимации, должны быть пространственными (3d), реалистичными, и геометрически точными [3]. Модели желательно присвоить материалы, облегчающие восприятие и доставляющие эстетическое удовольствие при просмотре. Свойства материалов, как правило, постоянны, но могут быть переменными и управляемыми программой.

Основная сложность программ, создающих анимацию, связана управлением геометрией модели. Этот этап требует разработки и программной реализации геометрического алгоритма построения модели и кинематического алгоритма преобразования модели между кадрами. Рассмотрим примеры.

2. Коническая прямозубая передача

Анимация (см. файл презентации, анимация 1, см. рис. 6, а) показывает согласованное вращение колес конической зубчатой передачи. Зацепление зубьев показано при плавном изменении направления взгляда вокруг колес, что повышает информативность фильма. Анимация предназначена для курса инженерной графики и деталей машин.

Прежде нужно в AutoCAD’е построить геометрически точную 3d модель передачи (рис. 1). Пример построения подробно приведён в [4, стр. 428]. Рис. 1, а – первый кадр анимации, рис. 1, б – последний кадр, рис. 1, в показывает геометрическую точность модели.

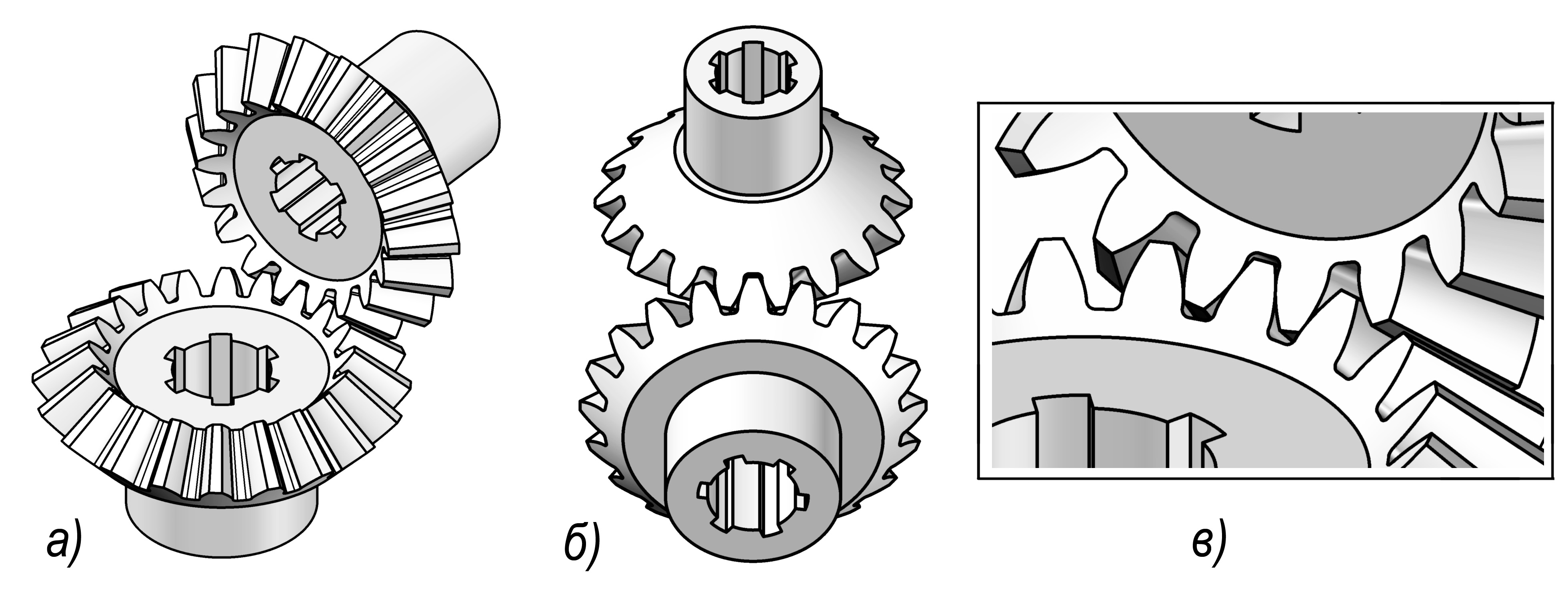
Рис. 1. Коническая прямозубая передача

Кадры анимации формируются программой 1. Приведем комментарии к этой программе.

В пакете AutoCAD, в файле, в котором построены шестерня и колесо, открываем Редактор Visual Lisp. Набираем текст программы. О правилах набора, отладки и выполнения программ – см. [4, стр. 199], [5, главы 12,13]. Устраняем неизбежные ошибки набора текста, причем Редактор активно помогает в этом своими подсказками. Загружаем программу и выполняем ее. Видим, как на экране колеса согласованно вращаются, при этом формируются растровые кадры, которые заносятся в предварительно указанную папку.

В программе предусмотрено, что колеса в начальном положении координированы относительно осей начальной системы координат (МСК). Шестерней названо колесо, имеющее 18 зубьев и ось, расположенную вдоль оси Х. Второе колесо (просто “колесо”) имеет 20 зубьев и ось вдоль Z.

Программа 1.

;;;========================================================

;;; Анимация вращения конических зубчатых колес

;;;========================================================

(defun c:ani_1 ( );_ главная функция

(mu_setup) ;_начальные настройки

(data_calc) ;_ввод данных и вычисления

(kinematics) ;_перестроение модели и покадровая съемка

(mu_restore) ;_восстановление настроек

)

(defun mu_setup ( ) ;_начальные настройки

(command "_undo" "_m") ;_создать метку

(setvar "cmdecho" 0) ;_отключить эхо-вывод

(setvar "osmode" 0) ;_отключить объектную привязку

(command "_mspace") ;_ перейти в пространство модели

)

(defun data_calc ( ) ;_ввод данных и вычисления

(setq name1 (car (entsel "\n Укажи шестерню ")) ;_имя объекта шестерни

name2 (car (entsel "\n Укажи колесо ")) ;_ имя объекта колеса

z1 18 ;_кол-во зубьев шестерни

z2 20 ;_кол-во зубьев колеса

w ( / z1 z2 1.) ;_передаточное число

n1 (getreal "\n Число оборотов шестерни = ")

n (getint "\n Количество кадров = ")

ang1 ( / (* 360 n1) n) ;_угол поворота шестерни на один кадр, градусы

ang2 (* ang1 w –1.) ;_угол поворота колеса

alf1 60 ;_горизонтальный угол зрения, начальное значение

alf2 –180 ;_горизонтальный угол зрения, конечное значение

bet1 60 ;_вертикальный угол зрения, начальное значение

bet2 –45 ;_вертикальный угол зрения, конечное значение

dalf ( / (– alf2 alf1) n 1.) ;_шаговые приращения углов зрения

dbet ( / (– bet2 bet1) n 1.)

num 101 ;_номер в имени 1-ого файла

i 0 ;_номер кадра

alf alf1

bet bet1

)

(defun kinematics ( ) ;_перестроение модели и покадровая съемка

(repeat n ;_цикл перестроения модели и покадровая съемка

(command "_ucs" "_w")

(command "_vpoint" "_r" alf bet) ;_изменение вида

(command "_plot" "" "" "" "" (itoa num) "" "");_сохранение кадра в растровом файле

(command "_rotate" name2 "" '(0 0) ang2) ;_поворот колеса

(command "_ucs" "_y" 90)

(command "_rotate" name1 "" '(0 0) ang1) ;_поворот шестерни

(setq alf (+ alf dalf)

bet (+ bet dbet)

num (1+ num)

i (1+ i)

)

(princ (strcat "\nКадр " (itoa i) " Осталось " (itoa (- n i)) " "))

)

(defun mu_restore ( )

(command "_undo" "_b") ;_восстановление начального положения колес

;;; ....;_команды восстановления предшествующих настроек

)

(defun c:mu ( )

(command "_undo" "_b");_отмена построений при аварийном сбое

)

(princ "\nДля выполнения введи ani_1");_сообщение при загрузке программы

;;;=============================================Конец программы 1

Программа 1 состоит из главной функции c:ani1 и четырех функций-подпрограмм. Назначение подпрограмм пояснено комментариями в тексте.

Функция data_calc выполняет запрос параметров анимации, которые нужно ввести в командную строку. Анимация 1 построена для n1 = 1 – одного оборота шестерни и n = 150 кадров.

Функция kinematics реализует цикл съемки из n кадров, выполняя согласованный поворот колес. Запись изображения экрана производит команда plot, которая должна быть предварительно настроена на запись в формате jpg или png в предварительно подготовленную папку [4, стр. 417] .

Поскольку команда plot сохраняет изображение, как оно выглядит на экране, то для красивой анимации необходимо задать и настроить визуальный стиль реалистичного изображения [4, стр. 338].

Программа 1 весьма проста. Если создана модель колес, то даже при начальном опыте программирования она сразу заработает. Можно скопировать текст программы в окно редактора Visual Lisp.

3. Косой цилиндр с тремя направляющими

По классификации кинематических поверхностей, приведенной С.А. Фроловым [6], это наиболее сложная линейчатая поверхность. Она формируется движением прямолинейной образующей, которая в каждый момент перемещения пересекает три предварительно заданные неподвижные пространственные криволинейные направляющие (рис. 2, а).

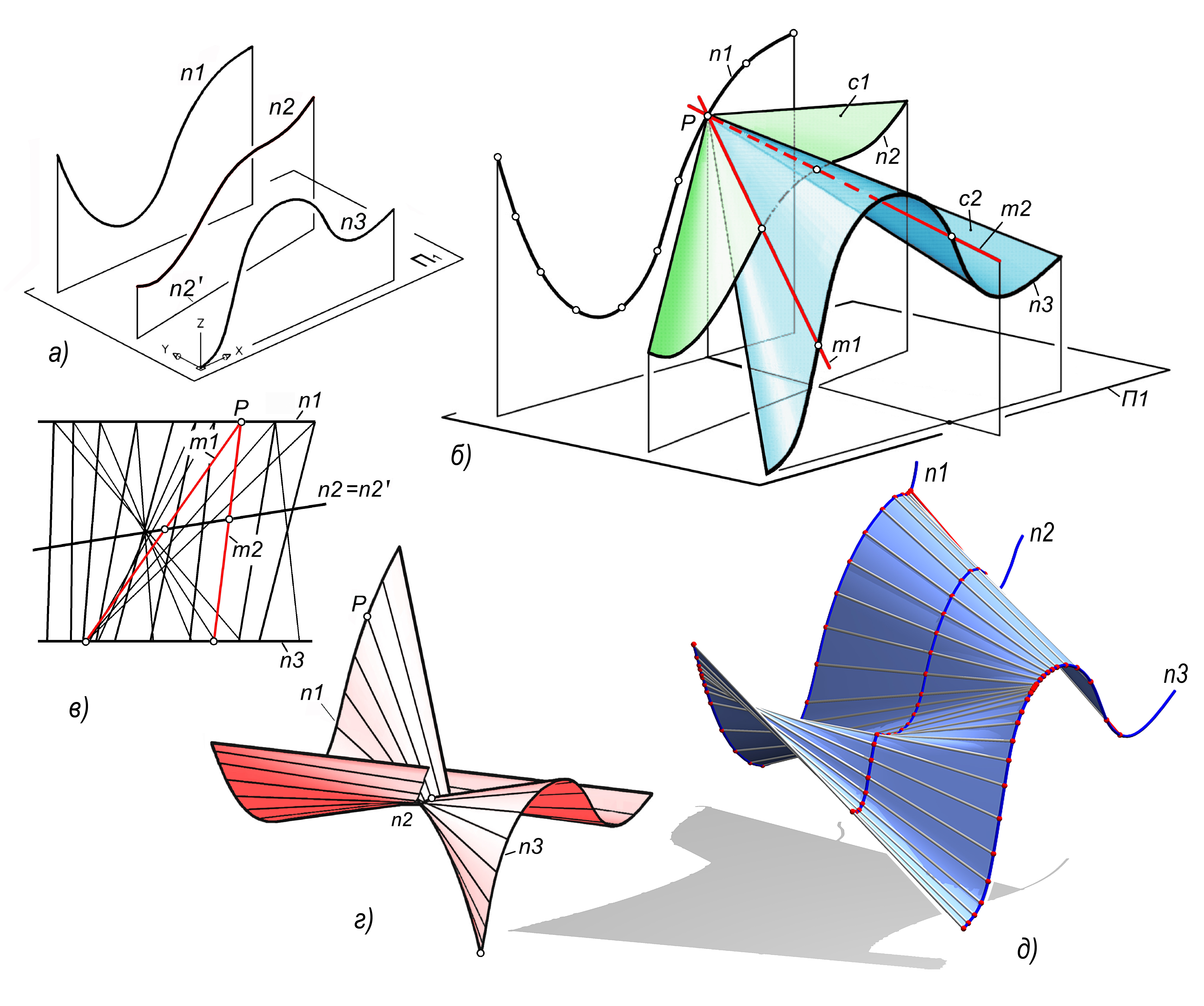
Рис. 2. Цилиндр с тремя криволинейными направляющими

В презентационном файле приведена анимация 2, показывающая формирование косого цилиндра как результат движения отрезка прямой, “скользящего” по трем направляющим (см. рис. 6, б). Отрезок тянет за собой поверхность.

В AutoCAD’е строим три направляющие n1, n2, n3 как сплайн-кривые. В нашем примере координаты точек, необходимых для построения сплайнов, приведены в работе [4, стр. 469]. Там же приведен пример построения всей поверхности в ее конечном виде при “ручной” реализации.

Для построения анимации необходима программа, воспроизводящая кинематику плавного движения отрезка образующей по направляющим согласно геометрическому 3d алгоритму формирования поверхности.

Алгоритм формирования поверхности косого цилиндра, с учетом его программной реализации, представим следующим образом, несколько отличающимся от [6, 7].

Предварительно проверяется существование неразрывной поверхности искомого цилиндра путем погружения одной из его направляющих в линейчатую конгруэнцию, образованную двумя другими [6, 8]. При полном погружении возможно получение неразрывной поверхности. Иначе поверхность будет иметь разрывы. В нашем примере была построена конгруэнция [9], заданная направляющими n1, n3, и проверено, что имеет место полное погружение в нее направляющей n2. То есть неразрывная поверхность при заданных направляющих существует.

Далее, на одной из направляющих, выбрана направляющая n1, задаем точки P (рис. 2, б). Количество этих точек определяет плавность формирования поверхности и количество кадров анимации. В нашем примере для плавной анимации количество точек, следовательно, кадров составило ≈50.

Из каждой точки как из вершины строим конусы c1, c2 с направляющими n2 и n3. Находим прямые пересечения конусов как их общие образующие. Положительная проверка по конгруэнции гарантирует в точках P наличие хотя-бы одной образующей. В примере (см. рис. 2, б) в точке P таких образующих две: m1 и m2. Каждая из них пересекает три заданные направляющие и поэтому является образующей искомого цилиндра.

В итоге построено множество образующих искомого цилиндра (рис. 2, в). Формируем наборы образующих, близко расположенных друг к другу. По каждому из них строим поверхности. При одних и тех же направляющих возможно множество вариантов поверхностей косого цилиндра. В нашем примере выявлено две наглядные неразрывные поверхности: одна из них с самопересечением (рис. 2, г, см. рис. 6, б), вторая – плавная поверхность без самопересечения (рис. 2, д). Другие варианты менее наглядны.

Анимация (см. анимация 2 презентационного файла и рис. 6, в) была построена для варианта плавной поверхности (рис. 2, д). Тот же рисунок является последним кадром анимации.

Рассмотрим меры повышения наглядности этой анимации, которые применены и в последующих анимациях.

Направляющие заданы как каналовые поверхности ⌀ 0.5 мм, образующие – как цилиндры того же диаметра, точки их пересечения с направляющими – заданы сферами ⌀1,5. Установлены два источника света: один теневой удаленный и источник подсветки. Тень от формируемой поверхности на плоскость “земли” подчеркивает кинематику формирования. Подобраны материалы, установлен фон. Элементы модели имеют различный цвет (материал).

В отличие от предыдущего примера программа анимации 2 является весьма сложной. Воспроизвести ее в тексте доклада не представляется возможным. Отметим лишь ее некоторые фрагменты и особенности. Часть из них можно найти в работах [4] [5, стр. 264].

Конусы заменены на пирамидальные поверхности. Отрезки m1, m2 определяются несложными алгоритмами как решение задачи о пересечении граней этих поверхностей. Найденные отрезки сортируются по взаимному положению на основе определения расстояния между их конечными точками на направляющей n3. Формируется оптимальный набор близкорасположенных образующих. По этому набору командой Loft строится поверхность c последовательным добавлением по одной образующей в каждом кадре. Вокруг каждой образующей программа дополнительно строит цилиндры и сферы с центрами в точках пересечения. Для каждого кадра выполняется фотореалистичная визуализация командой Render, настроенной на сохранение растровых файлов размером 1024 *768.

4. Однополостный гиперболоид

Однополостный гиперболоид (ОГ) – линейчатая поверхность. Формируется движением прямой линии (образующей), которая в каждый момент перемещения пересекает три предварительно заданные скрещивающиеся прямые (направляющие). Представить этот кинематический механизм непросто. Построена анимация формирования такой поверхности (презентационный файл, анимация 3, см. рис. 6, г).

В основе анимации лежит следующий геометрический алгоритм формирования ОГ.

Пусть заданы отрезки трех направляющих – попарно скрещивающихся прямых a, b, c. В нашем примере координаты направляющих приведены в [10]. На рис. 3, а приведен первый кадр анимации с этими направляющими.

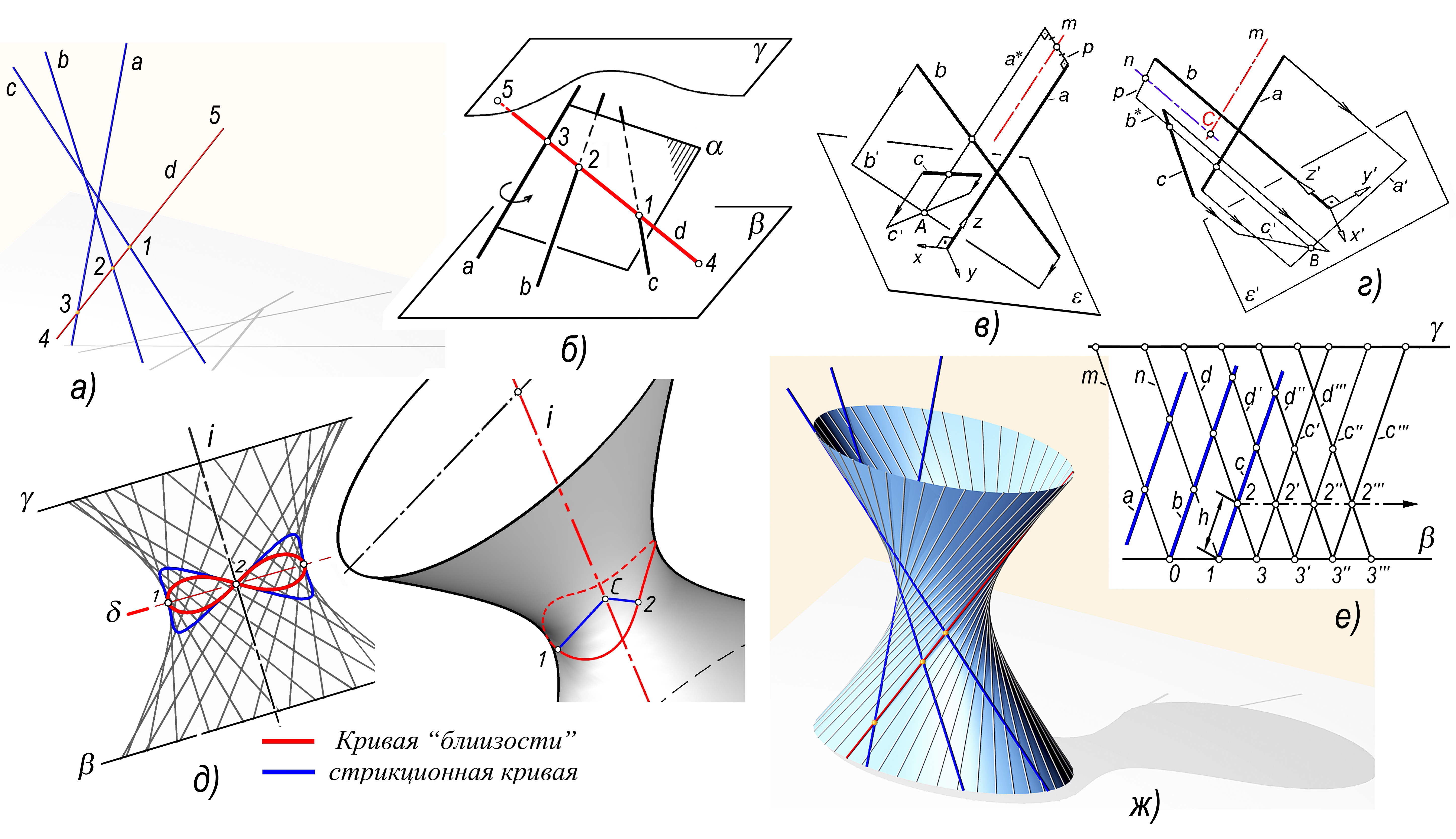
Рис. 3. Однополостный гиперболоид

Для построения множества образующих применим вращающуюся секущую плоскость α (рис. 3, б). Плоскость строим через одну из направляющих, например а. Находим точки пересечения 1,2 двух других направляющих с этой плоскостью. Прямая d(1,2) является одной из образующих искомого ОГ. Поворот плоскости α вокруг направляющей а позволяет построить множество всех образующих [5–7,10].

Однако реализация этого алгоритма выявила его существенные недостатки. При равномерном вращении плоскости α каркас из образующих получается крайне неравномерный. Неравномерность особенно проявляется при приближении плоскости к положению, параллельному одной из направляющих. Второй недостаток вращающейся плоскости – сложно сформировать наглядный отсек поверхности канонической формы. Поэтому потребовалась существенная доработка алгоритма, связанная с нахождением центра ОГ, плоскости его горловины и придания равномерности каркасу образующих. Для этого был разработан ряд геометрических алгоритмов.

Центр ОГ находим как точку пересечения двух “срединных линий” [10] согласно алгоритму [11]. Для построения срединной линии m решаем задачу о нахождении прямой, параллельной прямой a и пересекающей две скрещивающихся прямые b, c (рис. 3, в). Задаем плоскость ε перпендикулярную a. На эту плоскость строим проекции направляющих b, c, соответственно b‘, c‘. Находим точку A = b‘∩ c‘. Строим a* через точку A, a* параллельно a. Находим отрезок p перпендикулярный a и его среднюю точку M. Строим отрезок m через точку M, m параллельно a.

По тому же алгоритму находим вторую срединную линию n (рис. 3, г). Центр ОГ, точка C, определяется как пересечение прямых m и n.

Для нахождения плоскости горловины строим стрикционную кривую. Для этого вращающейся плоскостью генерируем 25–50 образующих. Находим отрезки кратчайшего расстояния между соседними образующими и соединяем их средние точки. Плоскость симметрии δ полученной линии (рис. 3, д), напоминающей “бабочку”, является искомой плоскостью горловины ОГ. В находится и найденный ранее центр ОГ, точка С.

Однако более простым оказался алгоритм, при котором горловина находится как плоскость симметрии кривой “близости”. Эту кривую, предложенную нами, строим, опуская перпендикуляры из центра ОГ, точки C, на предварительно найденные образующие. Плоскость горловины находим как δ (1,2,С), где 1,2 – соответственно наиболее и наименее удаленные точки кривой “близости”.

Строим ось ОГ как i перпендикулярную плоскости δ и проходящую через C. Строим плоскости β и γ оснований ОГ, параллельные δ.

Для построения равномерного линейчатого каркаса многократно решаем задачу о нахождении прямой, проходящей через заданную точку и пересекающую две скрещивающиеся прямые. Решение этой задачи позволяет найти образующую, проходящую через заданную точку одной из направляющих и пересекающую две другие направляющие, или найти направляющую, проходящую через заданную точку одной из образующих и пересекающую две другие образующие.

Обозначим d (1,a,b) прямую d, проходящую через точку 1 и пересекающую скрещивающиеся прямые a,b (см. рис. 3, б). Задача решается построением плоскости α (a, 1) и определением точки 2 = b∩α.

Пусть заданы три направляющие a,b,c. Согласно схеме (рис. 3, е) на направляющей c отмечаем точку 2 на заданном расстоянии h от точки 1. Строим образующие m(0,a,c); n (1,a,b) и d= (2,a,b). Далее реализуем пошаговое действие. Каждый шаг связан с переопределением точек 2,3. Шаг 1: c‘=(3,m,n); d ‘= (2 ‘,a,b). Шаг 2: c‘‘ = (3‘,m,n); d ‘‘=(2‘‘,a,b). Шаг 3: c‘‘‘= (3‘‘,m,n); d ‘‘‘= (2‘‘‘,a,b) и т.д. С каждым шагом к каркасу добавляется по одной образующей и направляющей. В итоге получаем равномерный каркас из направляющих и образующих, плотность которого определяется параметром h. Для анимации построен каркас только из образующих d, d ‘, d ‘‘, d ‘‘‘ и т.д. (рис. 3, ж).

Несмотря на сложность геометрического алгоритма ОГ, его программная реализация не представляет особой сложности, программа получается лишь громоздкой. Приведенные алгоритмы – характерны для решения задач геометрического моделирования на AutoLisp [5]. Основа рассмотренной программы ОГ приведена в [5, стр. 254].

Анимация ОГ (файл презентации, анимация 3) показывает движение образующей. Приведены два оборота образующей. В первом показано только перемещение образующей, во втором – формирование поверхности, которую тянет за собой образующая. Поверхность ОГ строим по набору образующих каркаса применением команды Loft с добавлением одной образующей к каждому новому кадру. Применены те же средства повышения наглядности, что и анимации 2 (свет, тени, материалы, вспомогательные объекты, воспроизводящие исходные направляющие и искомую образующую). Первый кадр анимации – см. рис. 3, а; последний кадр – см. рис. 3, ж.

5. Торс и его развертка

Поверхность торса образована перемещением отрезка образующей прямой по направляющей так, что в каждый момент образующая является касательной к направляющей. Направляющая – любая пространственная кривая [6, 7].

В нашей работе получена анимация двух торсов. Первый торс – эвольвентный геликоид с направляющей гелисой. Второй торс – общего вида с произвольной пространственной кривой в качестве направляющей.

Предварительно в AutoCAD должна быть построена пространственная кривая как траектория движения. Далее необходима программная реализация кинематики формирования торса. Программа построения 3d модели торса реализует следующее.

равномерное размещение точек на направляющей. Количество точек определяет дискретность модели, ее точность и плавность анимации;
задание направления касания к направляющей как вектора, соединяющего две рядом расположенные точки;
построение отрезка образующей по мере перемещения точки касания по направляющей;
построение поверхности по набору образующих и командой Loft или сдвигом образующей по траектории командой Sweep.

Программа построения торса для произвольной направляющей в упрощенном варианте приведена в [5, стр. 204] .

Для эвольвентного геликоида (анимация 4, см. презентационный файл, см. рис. 6, д) строим гелису (спираль, пространственная винтовая линия), которая предусмотрена во всех современных САПР. Параметры гелисы и длина образующей для нашего примера приведены в работах [4, стр. 408], [12]. При построении анимации реализованы все рассмотренные выше средства повышения наглядности. В анимации первоначально показано “скольжение” образующей по гелисе, затем вращение построенного торса вокруг оси гелисы.

Для второго торса должна быть подготовлена пространственная кривая. В нашем примере [12] направляющая – это линия пересечения сферы и кругового конуса (рис. 4, а). Для ее построения следует решить задачу на пересечение указанных тел и выделить линию как самостоятельный объект. Эти средства также имеются во всех САПР. Образуется пространственная кривая 4-ого порядка, реализованная как сплайн n.

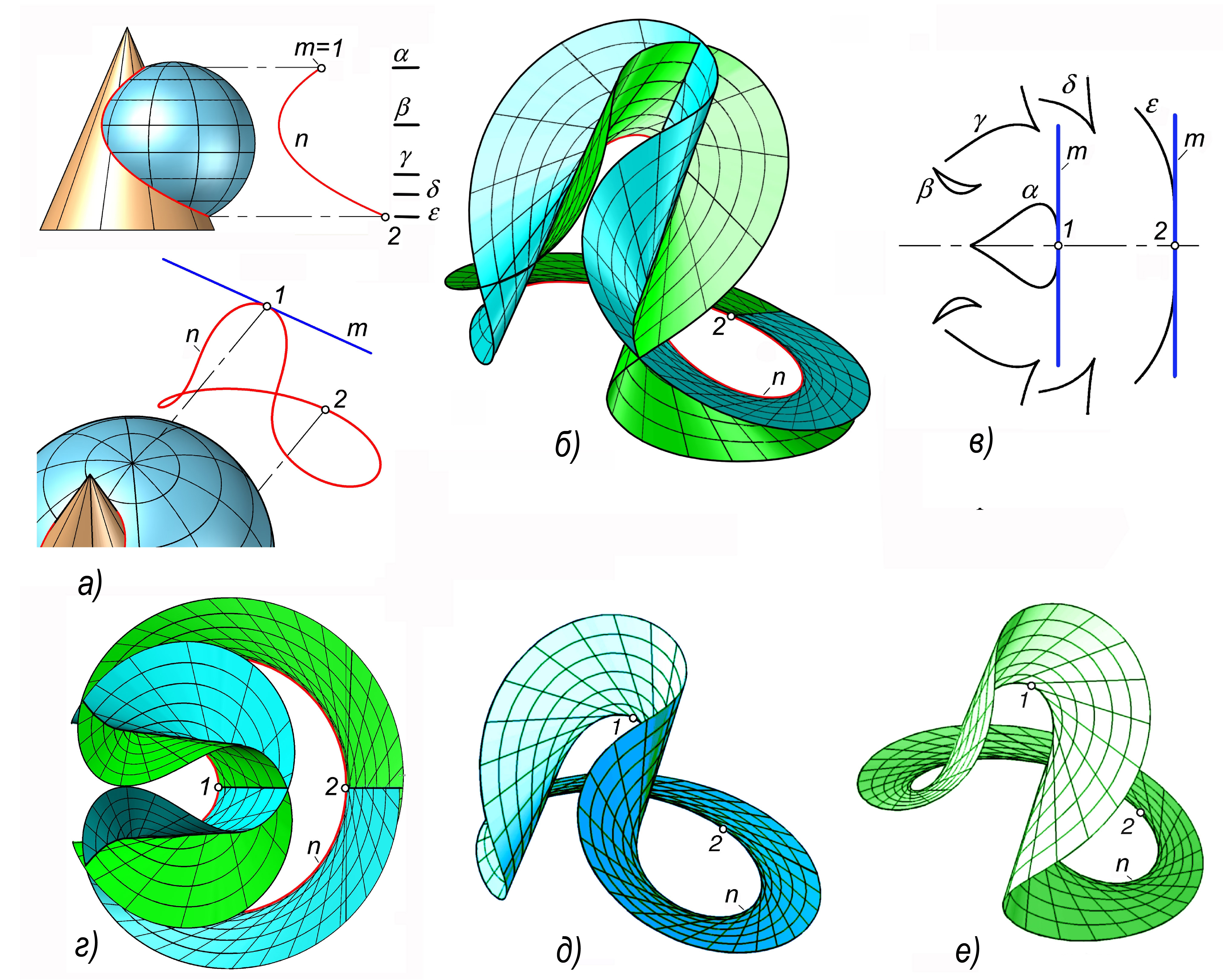
Рис. 4. Торс общего вида

При выполнении программы формируется поверхность торса, показанная в анимации 6 (см. презентационный файл, рис. 6, е).

В дополнение к анимации рекомендуем построить поверхность торса “вручную”. В AutoCAD’е для этого к направляющей n добавляем образующую m и применяем команду Sweep (Сдвиг) (рис. 4, б) [4, 12]. Далее можно исследовать эту красивую поверхность, например, построив ее сечения (рис. 4, в) или рассмотрев каждую половину торса в отдельности (рис. 4, г–е).

Какой же торс без развертки! Ее построение реализовано специальной программой, которая разбивает пространственные четырехугольники сегментов, образующихся между двумя последовательными положениями образующей m и m*, на треугольники (рис. 5, а).Например, 1-3-4-2-1 разбивается на 1-3-4 и 1-2-4. Затем треугольники поворачиваются (раскатка) вокруг общего ребра 1-4 и совмещаются в единую плоскость.

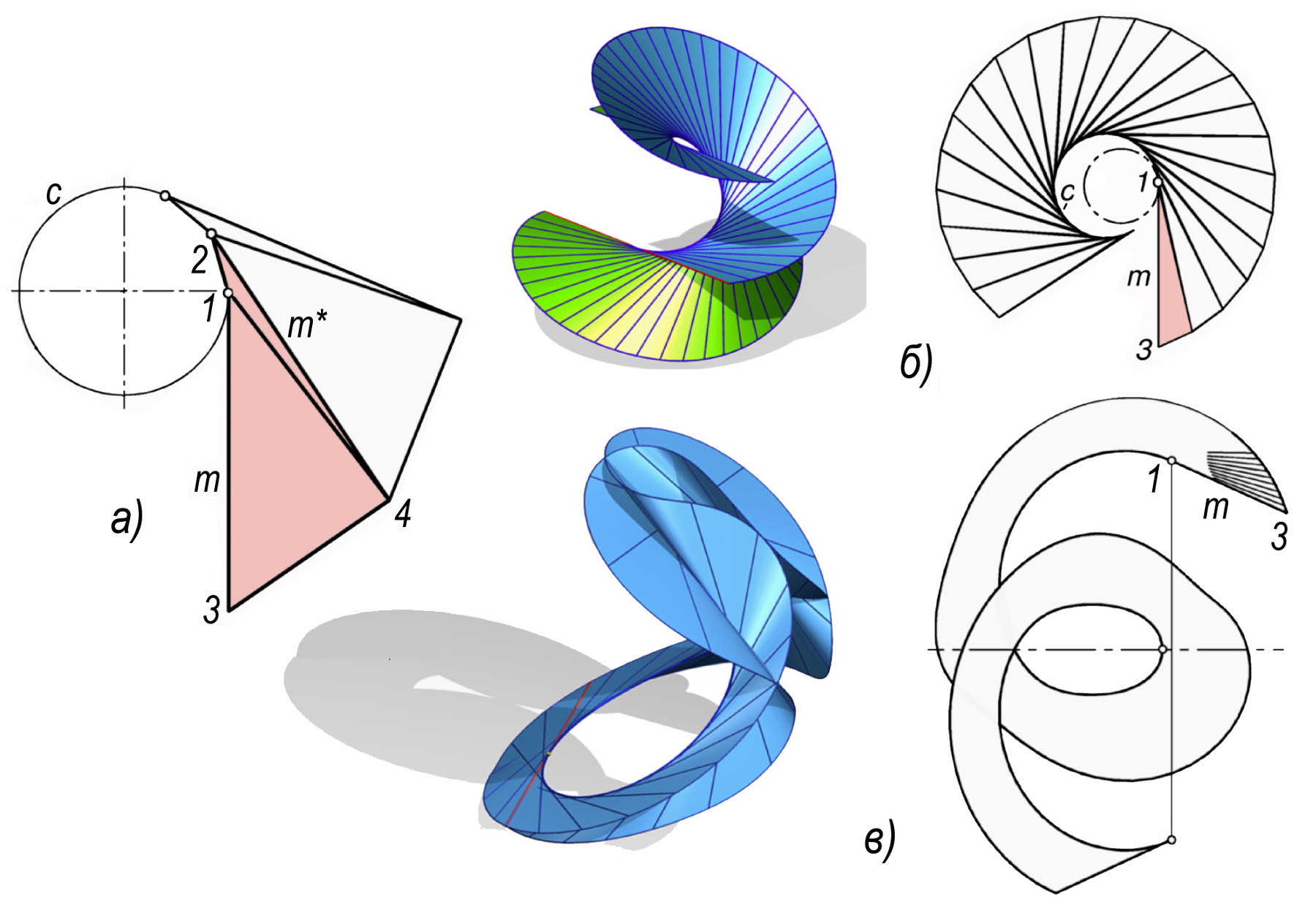
Рис. 5. Развертка торса

Эвольвентный геликоид разворачивается в два круговых сектора, один из них показан на рис. 5, б. В анимации (см. презентационный файл, анимация 5, см. рис. 6, ж) первоначально показано смещение вверх одной половины торса, что позволяет избежать наложения частей развертки. Затем выполняется раскатка обеих частей. Окончательно устанавливается вид, в котором отчетливо видны образовавшиеся два круговых сегмента.

Значительно более сложный вид имеет развертка торса общего вида. Во избежание наложения приведена развертка только одной его части (рис. 5, в).

На рис. 6 приведена сводная таблица, содержащая кадры рассмотренных анимаций.

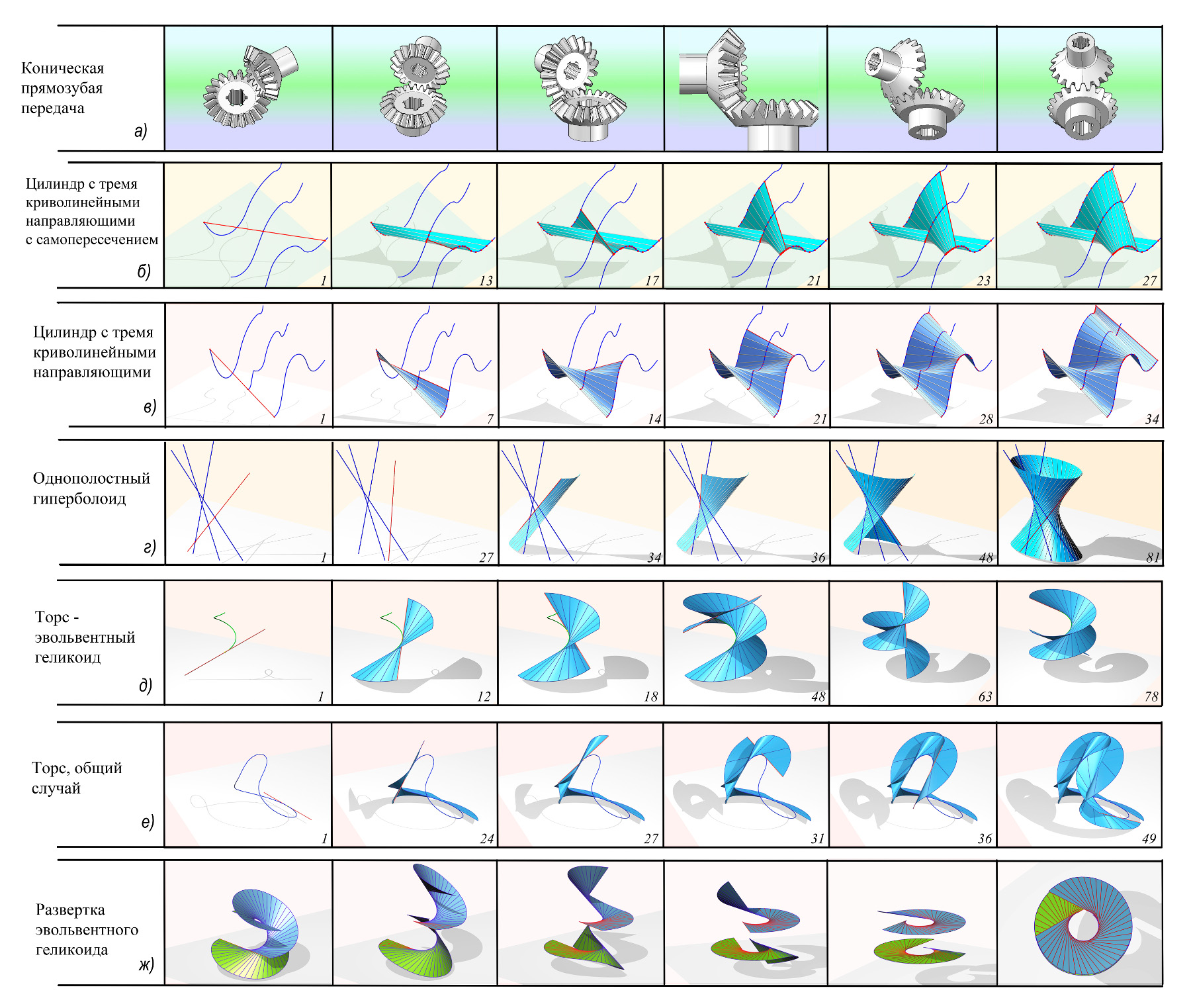
Рис. 6. Сводная таблица анимаций

Выводы:

Создание анимаций требует “глубокого погружения” в геометрический алгоритм отображаемой модели, разработки специальных алгоритмов, реализующих кинематику формирования модели, владения основами программирования.
Наиболее близким к решению задач геометрического моделирования и программирования для кафедр графики является AutoLisp в среде пакета AutoCAD.
Построение геометрически точных компьютерных 3d анимаций является эффективным средством совершенствования учебного процесса кафедр графики и одним из перспективных направлений их развития.
Получены файлы анимаций, приведенные в качестве презентации к докладу. Посмотрите эту презентацию и можете применять ее в своих лекционных курсах.

Список литературы

1. АВТОЛИСП – язык графического программирования в системе AutoCAD. http://kappasoft.narod.ru/info/acad/lisp/a_lisp.htm#L.

2. Гладков С.А. "Программирование на языке Автолисп в системе САПР Автокад". М.: "ДИАЛОГ-МИФИ", – 1991, – 96 с. http://www.knigka.info/2016/08/29/programmirovanie-na-jazyke-avtolisp-v.html

3. Хейфец А.Л. Геометрическая точность компьютерных алгоритмов конструктивных задач [Электронный ресурс] / А.Л. Хейфец // Материалы VI Международной научно-практической интернет конференции, Пермь, февраль-март 2016 г. – Пермский национальный исследовательский политехнический университет (Пермь). Вып. 3, – 2016, – с. 367-387. http://dgng.pstu.ru/conf2016/papers/74/

4. Хейфец А.Л. Инженерная 3d-компьютерная графика. Учебник и практикум для академического бакалавриата. / А.Л. Хейфец, А.Н. Логиновский, И.В. Буторина, В.Н. Васильева; под ред. А.Л. Хейфеца. – 3-е изд., пер. и доп. – М.: Изд-во Юрайт, – 2015. – 602 с.

5. Хейфец А.Л. Инженерная компьютерная графика. AutoCAD. Опыт преподавания и широта взгляда / А.Л. Хейфец. – М.: Диалог МИФИ, – 2002, – 432 с.

6. Фролов С.А. Начертательная геометрия / С.А. Фролов. – М.: ИНФРА-М , 2016, – 285 с.

7. Четверухин Н.Ф. Начертательная геометрия [Текст] / Н.Ф. Четверухин и др. – М.: “Высшая школа”, 1963, – 420 с.

8. Токарь А.Е. Графическое исследование линейчатой конгруэнции, определяемой двумя отрезками линий, и ее применение при конструировании линейчатых поверхностей общего вида / А.Е. Токарь // Вопросы начертательной геометрии и ее приложение: сб. науч. статей, под ред. Г. К. Николаевского. – Харьков:, Издат-во Харьковского университета.– 1963. – Вып. 3. – с. 60–67.

9. Хейфец А.Л. 3D-модель линейчатой поверхности с тремя криволинейными направляющими / А.Л. Хейфец, А.Н. Логиновский // Совершенствование подготовки учащихся и студентов в области графики, конструирования и стандартизации: Межвузовский научно-методический сборник. – Саратов: – Изд-во Саратовского гос. тех. ун-та.– 2008, – с. 13-19.

10. Хейфец А.Л. 3D-модели линейчатых поверхностей с тремя прямолинейными направляющими / А.Л. Хейфец, А.Н. Логиновский // Вестник Южно-Уральского государственного университета. Серия “Строительство и архитектура”. – Челябинск: Изд-во ЮУрГУ. – 2008. – Вып. 7. №25(125), с. 51–56. http://dspace.susu.ru/xmlui/bitstream/handle/0001.74/615/10.pdf?sequence=1&isAllowed=y

11. Короткий В.А. Метрические свойства поверхностей второго порядка: учебное пособие / В.А. Короткий. – Челябинск: Изд-во ЮУрГУ. – 2001, – 70 с.

12. Хейфец А.Л. 3D-модель торса / А.Л. Хейфец, А.Н. Логиновский // Проблемы геометрического моделирования в автоматизированном проектировании и производстве. 24-26 июня 2008. Сборник материалов 1-ой международной научной конференции. Москва 2008. Под. ред. В.И. Якунина. – М.: МГИУ. – 2008, – С. 390-394

Вопросы и комментарии к выступлению:

Иванов Геннадий Сергеевич (15 марта 2017 г. 0:20)	Александр Львович! Ваш доклад хорошо иллюстрирует возможности 3D анимации при изучении ряда вопросов курса начертательной геометрии, в частности, образование сложных поверхностей. Хотя тема не нова (я лично увидел подобную анимацию в 2002 году в Киеве на 10-ой конференции ISGG), но остается актуальной. К сожалению, доклад не лишен – небрежностей в изложении геометрических вопросов (при построении ребра возврата торса в виде линии пересечения «сферы и кругового конуса … следует решать задачу на пересечение указанных тел» (?), «цилиндр с тремя криволинейными направляющими» и др. - ошибки («при одних и тех же направляющих возможно множество вариантов (выделено мною) поверхностей косого цилиндра»). Эти поверхности многолистны: если направляющими a, b, c линейчатой поверхности ß являются алгебраические кривые соответственно порядков n₁, n₂, n₃, то сама поверхность ß будет порядка N = 2n₁n₂n₃, а ее направляющие a, b, c будут на ней соответственно n₂n₃-, n₁n₃-, n₁n₂- кратными, т.е. через a проходят n₂n₃ листов (пол), через b – n₁n₃ листов, а через c – n₁n₂листов. Эти листы могут быть действительными и мнимыми. Так что вы построили несколько отсеков одной и той же (!) поверхности ß. Кстати, на это обстоятельство я обратил Ваше внимание еще в 2008 году на конференции в МГИУ (там Вы, кажется, рассматривали цилиндроиды). Г.С. Иванов
Тен Марина Германовна (15 марта 2017 г. 7:32)	Александр Львович, большое спасибо за интересный доклад и за разрешение использовать презентацию в лекциях...На мой взгляд, все изложено доступным языком и у меня пробудился интерес к программированию в AutoCAD. Для студентов такие ролики - подарок..Наглядно и интересно....С уважением. Тен М.Г.
Головнин Алексей Алексеевич (15 марта 2017 г. 10:48)	Здравствуйте Александр Львович! Наглядность – важное направление в совершенствовании методики подачи материала начертательной геометрии, требующей повышенного пространственного воображения по сравнению с тем же геометрическим моделированием. Даже на этой конференции имеется широкий спектр отношения к этому направлению. От разработки целых курсов с ориентацией на наглядность до негативного отношения к тому, что учебники содержат «цветные картинки и фотографии». За рубежом (Украина года теперь тоже зарубежье) анимация занимает достойное место в образовательном процессе и не останавливалась в 2002 году. Пример – Серия видеороликов под общим названием «Размерность», ссылку на которую мы приводили на этой конференции. Ваша работа, с учетом содержания выступления Вашего уважаемого оппонента Геннадия Сергеевича Иванова, – первая такая попытка в нашем профессиональном сообществе. При чтении Вашего доклада сразу возникли аналогии с электронными учебниками уважаемых Константина Анатольевича Вольхина и Вячеслава Трофимовича Тозика, которые мы много лет рекомендуем студентам для самостоятельного изучения. Пользуясь случаем хочется высказать им слова благодарности за предоставляемую много лет возможность свободного доступа к ним. Ваша презентация, на наш взгляд, вместе с учебником К.А.Вольхина, и, возможно другими, неизвестными нам электронными материалами, должна послужить повышению качества обучения нашим предметам. Учебник В.Т.Тозика, к сожалению, мы в открытом доступе найти не смогли, вспомнили, что об этом уже с сожалением говорилось. При чтении Вашего доклада столкнулись с новыми для себя поверхностями, будем говорить о них студентам. С благодарностью принимаем Ваше приглашение использовать Вашу презентацию в учебном процессе. Как мы поняли, замечания уважаемого Г.С. Иванова об ошибках в докладе, никак не относятся к ее содержанию и к иллюстрациям, также представляющим ценность для учебного процесса. Еще раз спасибо за большую и очень полезную для нас, преподавателей начертательной геометрии работу. С уважением Головнин А.А.
Селиверстов Александр Владиславович (15 марта 2017 г. 11:31)	Здравствуйте, Александр Львович! Начну с замечания, что Геннадий Сергеевич не ошибается. 1) Обычно цилиндром называют поверхность, проективное замыкание которой является конусом с вершиной, принадлежащей бесконечно удалённой плоскости. В некоторой системе координат цилиндр - это множество нулей функции от двух (или всего одной) переменной. В книге (Фролов С.А. Начертательная геометрия. М. 1983. С.97) косой цилиндр с тремя направляющими - это общая линейчатая поверхность. Косой цилиндр может не быть цилиндром в смысле первого определения. Примером служит однополостный гиперболоид. Итак, в подписи к рисунку 2 "Цилиндр с тремя криволинейными направляющими" не хватает слова "Косой". Лучше бы эту поверхность называть иначе, но этот термин уже используется. 2) Если направляющими служат алгебраические кривые, то в общем случае линейчатая поверхность неприводимая. Даже если неприводимая поверхность имеет несколько вещественных компонент связности, все они определяются одним и тем же алгебраическим уравнением. В этом случае говорить о множестве вариантов не стоит. Впрочем, формально здесь нет ошибки, поскольку множество может состоять из одного элемента, а может быть и пустым. При таком понимании фразы ошибки нет, но и толку нет. Однако если рассматривать не обязательно алгебраические поверхности, то гораздо труднее провести отличие одной поверхности из двух компонент от двух разных поверхностей. (Поскольку существуют гладкие функции к компактным носителем.) Это требует терминологической точности, но в докладе об этом не сказано, возможно, из-за ограничений на размер текста. 3) Вы пишете: "Однополостный гиперболоид... Представить этот кинематический механизм непросто." Легко как представить, так описать без формул. Рассмотрим три прямые (направляющие) в общем положении. Выберем точку на первой прямой. Через эту точку и другую прямую проходит единственная плоскость. В общем случае две такие плоскости пересекаются по единственной прямой. Итак, каждой точке на первой прямой (направляющей) соответствует другая прямая (образующая), лежащая на проективном замыкании поверхности. Видимо, здесь трудность в построении красивой анимации, или нет? Читая доклад по геометрии, пытаюсь представить себе, как объяснить эту тему студентам. Раздел 4 мне показался перегруженным необязательными деталями, отвлекающими внимание. Возможно, упустил что-то важное именно для анимации? 4) К сожалению, гиперссылки на материалы конференции прошлых лет устарели. Кроме сборника докладов, уже не доступны ни комментарии, ни презентации прошлых лет. Поэтому красивую презентацию предлагаю сохранить где-нибудь ещё, пока она не пропала. В целом доклад хороший. С уважением, А.В. Селиверстов
Селиверстов Александр Владиславович (15 марта 2017 г. 13:14)	Александр Львович! В моём комментарии при описании гиперболоида в пункте (3) напрасно упоминается проективное замыкание: образующая лежит на аффинном гиперболоиде. Извините. С уважением, А.В. Селиверстов
Горнов Александр Олегович (16 марта 2017 г. 0:01)	Здравствуйте, Александр Львович! Спасибо за очередную иллюстрацию возможностей компьютерной визуализации геометрических задач в разнообразных статических и динамических режимах для инженерной, архитектурной и дизайнерской подготовки. Всем, в принципе, известны возможности компьютерного моделирования в разных сферах и на основе различных графических систем. Но Ваша целенаправленная работа в области, непосредственно примыкающей к ГГП, выделяется. Вызывает уважение набор средств, которыми Вы владеете и широко применяете. Полагаю, что это является фактором, увлекающим студентов, повышающих их мотивацию к овладению соответствующим материалом. Не слайд - проекционные картинки в компьютерной реализации, а анимация, методически продуманная - это, безусловно, высокий уровень иллюстративного обеспечения занятий. В связи с этим и вопрос: не инициируют ли студенты какие либо формы дополнительного изучения компьютерных технологий и хватает ли у Вас сил и поддержки для этого? Нельзя не видеть широкий спектр задач, которые Вы ставите и решаете, открытость Ваших материалов и результатов для коллег. C уважением, А.О.
Хейфец Александр Львович (16 марта 2017 г. 7:00)	Александр Олегович, приветствую Вас. Благодарен за, как я понял, высокую оценку моего доклада и, в целом, моей работы. Подчеркну, что в докладе я стремился показать анимации не только как эффектную и эффективную методическую разработку. Цель была и обратить внимание на создание анимаций как интересного, перспективного нужного в учебном процессе и доступного направления методической работы преподавателей наших кафедр. Освоить программирование – “не страшно” и доступно. При этом открываются такие горизонты, что “дух захватывает”. И еще я хотел показать, что 3d моделирование – это не нажатие кнопок, как стремятся его опорочить мои оппоненты, присутствующие и здесь на конференции и сами кроме этого мало что умеющие в 3D. Сама модель не заработает. От автора требуется глубокое понимание и реализация геометрических алгоритмов. В духе замечаний оппонентов отвечу: строить 3d модели – это не формУлы писать и любоваться ими, и не блистать терминологией, мало кому знакомой из-за ее невостребованности, и не придумывать несуществующие мнимые объекты, чтобы показать свою особость. Это реальные задачи, для которых в полной мере нужно знать ГЕОМЕТРИЮ. На Ваш вопрос: "не инициируют ли студенты какие либо формы дополнительного изучения компьютерных технологий и хватает ли у Вас сил и поддержки для этого?". - Конечно, инициируют. Вся моя работа инициирована потребностями учебного процесса. Александр Олегович, благодарю за комментарий к моему докладу. На остальные комментарии ответы готовлю. Выложу завтра. А.Л. Хейфец
Селиверстов Александр Владиславович (16 марта 2017 г. 18:41)	Здравствуйте, Александр Львович! Вы правы, строить 3D модели полезнее и труднее, чем попусту блистать терминологией. Но поскольку об этом зашла речь, длинное название "косой цилиндр с тремя направляющими" хорошо бы заменить коротким и выразительным. Тем более, что обучение пока не стало исключительно дистанционным; и названия приходится произносить вслух. Итак, близкое понятие - это свиток. Этот термин использован (в русском переводе) книги Дж. Харриса Алгебраическая геометрия. Начальный курс. Видимо, название свиток не является общепринятым. Впрочем, однажды уже услышал в ответ, что это и не важно, поскольку можно сказать по-английски. Ещё замечу, что нашёл упоминание об учебнике по НГ: "Сергей Аркадьевич Фролов * один из самых выдающихся представителей лысенковщины в н. г., автор безграмотного и претенциозного учебника". https://www.proza.ru/2002/10/02-13 Надеюсь, такой комментарий о терминологии никого из участников конференции не обидел. Пожалуйста, поправьте, если я ошибаюсь. С уважением, А.В. Селиверстов
Головнин Алексей Алексеевич (16 марта 2017 г. 20:46)	Пронзительно искренняя исповедь. Раньше не обращал внимание на эти слова, но такое чувство, что вопрос о соотношении математики и начертательной геометрии на кафедрах инженерной графики возникал и тогда: «… все время общаясь с математиками, я не обольщался. Там я был «рядовой, необученный». Когда я на фоне своих малограмотных коллег начинал сам перед собой задирать нос (перед ними я не задирал), то встречи с математиками были для меня холодным душем. И я почти соглашался с Дьедонне, что начертательная геометрия * задворки математики, и что гордиться мне нечем.»
Хейфец Александр Львович (17 марта 2017 г. 0:42)	Алексей Алексеевич, я правильно понял, что приведенная Вами цитата об оценке математиками наших "математиков" взята из мемуаров В. Пеклича? Это важно подчеркнуть, поскольку В. Пеклич имел математическое образование, в отличие от наших. К тому же В. Пеклич - это В.ПЕКЛИЧ. Его книги - настольные у многих (и у меня тоже). Любопытно, понимают ли наши "математики" это , то есть как их рассматривают математики? Есть ли у "наших" публикации в истинно математических журналах, а не только в ГиГ и аналогичных ей (ГиГ), да и наей конференции, где они согласно известной басне хвалят друг-друга. (Конечно, этот комментарий не к Вам, Алексей Алексеевич, просто оно навеян Вашей замечательной репликой). А.Л. Хейфец
Кокарева Яна Андреевна (17 марта 2017 г. 1:28)	Уважаемый Александр Львович, большое спасибо Вам за такую красивую презентацию и за возможность "заглянуть внутрь" процесса создания анимаций. Наглядно и воодушевляюще! С уважением, Кокарева Я.А.
Головнин Алексей Алексеевич (17 марта 2017 г. 10:32)	Здравствуйте Александр Львович! Да, эта цитата, из мемуаров В.А.ПЕКЛИЧА (цитирую Вас). Я не дал ссылку, потому, что привел эту цитату сразу после цитаты уважаемого Александра Владиславовича, который ссылку дал. Я несколько раз перечитывал эти мемуары. Приведенную цитату раньше не замечал, сейчас бросилась в глаза. Вообще в доме была целая серия биографий (Эйнштейн, Патон и др.), в детстве любил читать эти книги. Кстати, единственная книга с автографом автора у меня дома, это – сборник задач В.А.Пеклича 1998 года. Посчастливилось один раз общаться, мне это общение запомнилось, хотя раньше о нем не слышал. С уважением Головнин А.А.
Селиверстов Александр Владиславович (17 марта 2017 г. 13:42)	Здравствуйте, Александр Львович! Анимация поверхностей очень красивая и новая. (О зубчатых колёсах судить не берусь.) Видимо, я не умею хвалить, увы. Сработало досадное разделение на дисциплины. Но "мы должны (стремиться) понимать, что делают наши коллеги" (это цитата из http://ium.mccme.ru/globus.html ) Конечно, это относится ко мне! Позже попробую написать подробнее. Спасибо за указание на статьи В.А. Пеклича (к. от 3 марта 2017). Лишь недавно получил их в ГПНТБ. С уважением, А.В. Селиверстов
Хейфец Александр Львович (18 марта 2017 г. 12:06)	Александр Владиславович, Геннадий Сергеевич, Как я понял, мой доклад по анимации вызвал интерес с позиции терминологии и связанным с ней подсчетом параметров. Еще немного об этом добавлю. Возможно, будет интересно и другим коллегам. Подсчет параметров, как я понимаю, определяет лишь возможность решения и возможное их количество, то есть только необходимое условие существования решения. Достаточность при этом не гарантирована. То есть решение возможно, но оно может быть не действительным. Что, неужели опять мнимые решения! Зачем и кому это нужно. В рассмотренной задаче о косом цилиндре достаточность определяется исследованием конгруэнций направляющих, что в моей работе сделано. Из него вытекает либо отсутствие решения, либо множественность действительных решений. Так зачем же подсчет параметров? Экспериментатор в ходе исследования всегда определяет область действительного решения, но это будет установленный факт, а подсчет параметров - только теоретическая возможность этого. Поэтому я критически отношусь к прикладной стороне исчислительной геометрии. Там много своих тонкостей и, как и всякие уравнения, они дают теоретикам зачастую “что нужно” (“что дышло…”). Вот такие мои мысли по исчислительной геометрии как экспериментатора, а не теоретика начертательной геометрии. Жду комментариев. С уважением. А.Л. Хейфец
Селиверстов Александр Владиславович (18 марта 2017 г. 14:38)	Здравствуйте, Александр Львович! Вы правильно заметили, что в общем случае cуществование вещественных образующих нужно проверять отдельно! Это интересная и нетривиальная задача, что удачно отмечено в докладе. В частном случае, когда направляющими служат плоские кривые нечётной степени, это сводится к теореме Безу. Если же степени всех направляющих чётные, то вещественных образующих может не быть. Например, если направляющие -- три окружности маленького радиуса, не лежащие вблизи одной прямой, то нельзя провести ни одной вещественной образующей, которая пересекала бы все три окружности. Этот вывод не получается из подсчёта параметров. Однако подсчёт параметров может служить хотя бы для предостережения о возможных трудностях при визуализации. С уважением, А.В. Селиверстов
Иванов Геннадий Сергеевич (19 марта 2017 г. 19:52)	Александр Львович! Вы, отвечая на мои замечания по Вашему докладу, проявили недюжинную изворотливость в выборе места размещения ответа, а также его содержания с целью отрицания допущенного Вами очевидного геометрического «ляпа». Ваши слова «При одних и тех же направляющих возможно множество вариантов поверхностей косого цилиндра» равносильны отрицанию известного даже первокурсникам технических вузов факта, что линейчатая поверхность однозначно определяется заданием трех направляющих. Кстати, проф. А. Л. Хейфец, Вы даже в этом небольшом по объему ответе проявили свои «геометрические способности»: «Мне было достаточно проверки на конгруэнтность». По – видимому, Вы хотели сказать «на коллинеарность». Г.С. Иванов
Хейфец Александр Львович (19 марта 2017 г. 22:34)	Геннадий Сергеевич, По поводу однозначности Ваше замечание спорно. Посмотрите в докладе рис. 2. г и рис. 2, д. При единых направляющих приведенные поверхности имеют совершенно различные геометрические свойства. Насколько я понял, с Ваших позиций это однозначные, но многолистные поверхности. В любом случае это не повод для такого тона замечаний. О конгруэнтности. Именно проверку на конгруэнтность я и выполнил. Посмотрите учебник С.А. Фролова, стр. 95, рис. 127, 128. И много других работ, где первоначально выполняется проверка на конгруэнтность. Коллинеарность здесь не причем. И сдерживайте свои эмоции, пожалуйста. Хорошо бы увидеть Ваши извинения. А.Л. Хейфец
Селиверстов Александр Владиславович (20 марта 2017 г. 1:14)	Здравствуйте, Геннадий Сергеевич и Александр Львович. Спор отчасти вызван терминологической путаницей. В целом "линейчатая поверхность однозначно определяется заданием трех направляющих", но отдельные части этой поверхности не похожи друг на друга. Можно ли называть часть поверхности поверхностью? Если ограничиваться алгебраическими поверхностями, то нельзя. Однако на стр. 98 в учебнике С.А. Фролова (издание 1983 года) говорится: "Для образования поверхности косого перехода в качестве направляющих берут дуги окружностей одинакового радиуса..." Здесь рассматриваются уже не окружности, а только дуги (то есть части). Кстати, в этом учебнике не нашёл утверждения об однозначности определения. Удачна эта терминология или нет, но она приведена в учебнике, одобренном Министерством и получившим широкое распространение. Видимо, инженеров и архитекторов не слишком волнует формальная строгость применяемых ими терминов, если они понятны при разумном и доброжелательном толковании. На стр. 95 того же учебника говорится: "Форму и положение третьей направляющей выбирают так, чтобы она находилась внутри конгруенции прямых, определяемой двумя уже взятыми направляющими". И далее: "Под конгруенцией прямых подразумевается множество прямых, зависящих от двух параметров". (Здесь употребление буквы "е" вместо "э" соответствует учебнику.) Можно было сказать не о проверке на конгруэнтность, а о проверке существования конгруэнции. Однако это написано в комментарии, а не в основном тексте доклада. В тексте доклада говорится именно о конгруэнции (а не конгруэнтности). Может быть спор разгорелся из-за употребления в комментарии предлога "на"? Таким образом, остаётся лишь призвать участников спора к большей терпимости к чужому мнению, в частности, к мнению Сергея Аркадьевича Фролова. С уважением, А.В. Селиверстов
Иванов Геннадий Сергеевич (20 марта 2017 г. 23:31)	Уважаемый Александр Владиславович! Большое спасибо за комментарий к нашему спору с Александром Львовичем и за добрый совет о терпимости. См. мой ответ на последний комментарий А.Л. Хейфеца. Там я объясняю суть наших разногласий. Г.С. Иванов
Иванов Геннадий Сергеевич (20 марта 2017 г. 23:38)	Александр Львович! Давайте не будем требовать извинений друг от друга! Мой резкий ответ Вы спровоцировали своими словами «… является бантиком для украшения работы и придания ей наукообразия». Далее по существу. Согласен с Вами: «коллинеарность» здесь не причем. Это предположение вызвали Ваши слова «проверка на конгруэнтность». Термин «конгруэнтность» является синонимом слова «равенство» (см. О.В. Мантуров и др. Толковый словарь математических терминов. М., Просвещение, 1965). У меня, естественно, возник вопрос: «При чем здесь равенство?» И я предположил, что Вы имеете в виду принадлежность (коллинеарность) трех точек пересечения образующей с направляющими. (у Вас ведь два тела пересекаются по линии – Autocad здесь не причем). А Вы, оказывается, под этими словами имели в виду существование конструируемой (из конгруэнции) поверхности действительных образующих. Только после ссылки на учебник С.А. Фролова в Вашем последнем комментарии я понял суть Ваших заблуждений, и, как следствие, наших разногласий. Сначала небольшой исторический экскурс. Учебник С.А. Фролова я очень внимательно прочитал сразу же после выхода в свет первого издания в 1978 году. Экземпляр учебника с моими многочисленными замечаниями (подстрочными и на полях) почти на каждой странице, вернул автору. Возможно, этот экземпляр сохранился у Андрея Сергеевича, сына С.А. Фролова. С тех пор, образно говоря, этот учебник до сегодняшнего дня в руки не брал и, естественно, в целом забыл и его содержание, и свои замечания. Теперь несколько слов к сведению Александра Владиславовича. В Советском Союзе, а сейчас в России и странах ближнего зарубежья, существовали(ют) две школы начертательной геометрии (НГ): гордоновская и четверухинская. Школу В.О. Гордона отличает догматическая позиция: НГ – это сугубо графическая дисциплина, аналитика (тем более мнимости) – это математика; многие представители этой школы геометрию отождествляют с графикой; завет Г. Монжа о полезности совместного изучения «геометрии и алгебры» не признают. Кстати, теперь и в школе учат, что квадратное уравнение, имеющее отрицательный дискриминант, не имеет решения. Школа Н.Ф. Четверухина (доктора физмат наук, академика АПН СССР), следуя заветам Г.Монжа, считает, что в геометрии (в том числе и в НГ – как разделе геометрии) есть два противоположных, но взаимодополняющих метода исследования: синтетический (конструктивный, в частности, графический) и аналитический. Проф. С.А. Фролов, А.Л. Хейфец, как яркие представители гордоновской школы, считают, что линейчатая поверхность должна содержать только действительные прямые. Поэтому, признавая, что линейчатая поверхность однозначно определяется тремя направляющими, добавляют: «Произвольно можно задавать только две направляющие, форма и положение третьей направляющей выбирается так, чтобы она находилась внутри конгруэнции прямых, определяемой двумя уже взятыми направляющими (С.А. Фролов). А. Л. Хейфец это условие, как я теперь понял, называет «проверкой на конгруэнтность». С позиций теории конгруэнций этому условию отвечают конгруэнции первого порядка и k- класса Кг (1, k) (читателя, не знакомого с теорией конгруэнций, следовало бы отослать к многотомному труду классика линейчатой геометрии Рудольфа Штурма). Но он там обязательно «утонет». Поэтому я нескромно посоветую посмотреть 5-ю главу моего учебного пособия «Теоретические основы начертательной геометрии», написанного по материалам лекций на ФПКП МАИ, прочитанных в 1977 – 1990 гг. В этом случае через любую точку третьей направляющей обязательно будет проходить одна действительная образующая конструируемой линейчатой поверхности. Но загвоздка в том, что фокальными (сингулярными) линиями такой конгруэнции будут прямая a и пространственная кривая k-го порядка, для которой прямая a является (k-1) – секантой (проф. А.Л. Хейфец опять обвинит меня в наукообразии). Этот факт не согласуется с ошибочным утверждением Сергея Аркадьевича и Александра Львовича о произвольном задании первых двух направляющих для получения линейчатой поверхности только с действительными образующими. Однополостный гиперболоид получается из конгруэнции Кг (1, 1), поэтому имеем великолепную анимацию. Торсовая поверхность образуется из конгруэнции бисекант, но она не относится к косым цилиндрическим поверхностям, поэтому их красивая анимация «не работает» на автора доклада. Когда мы, представители четверухинской школы, говорим, что линейчатая поверхность однозначно задается любыми тремя направляющими, имеем в виду, что она содержит как действительные, так и мнимые образующие. Проф. А.Л. Хейфец, выполняя «проверку на конгруэнтность», получает не множество вариантов поверхностей косого цилиндра, а некоторые отсеки (листы) одной (!!!) поверхности, состоящие только из действительных образующих. В этом заключается его ошибка и, как следствие, наши разногласия. Г.С. Иванов
Хейфец Александр Львович (23 марта 2017 г. 20:07)	Геннадий Сергеевич, попытаюсь подвести итог в нашей полемике на этой конференции. Напомню, что тема моего доклада – изложение методики и примеров построения анимаций. Один из примеров доклада – косой цилиндр с тремя криволинейными направляющими – вызвал Ваш резкий комментарий в связи с моими терминами. В частности, я назвал эту поверхность многовариантной, поскольку привел очевидно различные варианты ее реализации. Вы указали, что согласно теории это все-таки единая поверхность, но многолистная. Я ссылался на трактовку С.А. Фролова, Вы привели ссылку на свою работу ”Теоретические основы начертательной геометрии”. Нас пытался успокоить уважаемый Александр Владиславович, который подчеркнул, что причина спора – лишь различие в формулировках. Мои выводы по нашей полемике. Я сожалею, что не привел ссылку на Вашу работу, пропустил, бывает. На меня тоже многие не ссылаются, хотя пишут о том, что уже давно мною опубликовано. И на этой конференции я неоднократно это отмечал. Я невольно заступил на “Вашу территорию” и вызвал такое негодование. Теперь Вы можете понять мои резкие высказывания в адреc тех (и в Ваш тоже) кто не зная 3d, критикует это современное направление в геометрическом моделировании. Знание я определяю по публикациям на данную тему (которых у Вас нет), по репликам, которые свидетельствуют, что оппоненты (и Вы тоже) в 3d САПР не работают. Полемика для меня была полезной, надеюсь, и Вам тоже. В частности, меня заинтересовало, можно ли вычислить количество действительных решений (например, косого цилиндра) из общего их количества, определяемого подсчетом параметров. Естественно, до начала выполнения экспериментальных построений. И последнее. Мне лестно, что Вы меня поставили в один ряд с Сергеем Аркадьевичем Фроловым и записали в школу В.О. Гордона. Да, я живу в реальном мире и признаю действительные решения. Мнимости воспринимаю как формальные результаты для наукообразия работ. Это при том, что Н.Ф. Четверухина я уважаю и считаю, что весь традиционный учебный процесс по НГ построен на его учебнике 1956 г. Может, Вам написать в ГиГ статью о двух школах. Будет полезно нам всем. С уважением. А.Л. Хейфец.
Иванов Геннадий Сергеевич (24 марта 2017 г. 0:15)	Александр Львович! Где Вы вычитали, что я критикую 3D? Я всего лишь против догматического, ненаучного противопоставления различных видов изображений, получаемых по схеме классического метода двух изображений! (Прочитайте стаью В.А. Короткого «Учебное задание “пространства различной размерности”», в которой он грамотно объяснил суть вопроса). Более того, я убежденный сторонник изучения начал многомерной (nD) геометрии для установления межпредметных связей между начертательной геометрией, линейной алгеброй и смежными разделами высшей математики. Там ведь тоже надо уметь изображать! Вспомните, с чего начался наш разговор на этой конференции. Я считаю, что мнение о начертательной геометрии лишь как об обеспечивающей дисциплине курсов инженерной и компьютерной графики, принижает ее роль в системе высшего образования. Результаты исследований, выполненных за последние 50-60 лет в рамках специальности 05.01.01, на мой взгляд, убедительно свидетельствуют о возможностях инженерной геометрии, в состав которой органично входит начертательная геометрия. Г.С. Иванов.
Суфляева Наталья Евгеньевна (28 марта 2017 г. 18:13)	Уважаемый Александр Львович! Я случайно отбрала у Вас приоритет в решении задачи о правильном треугольнике. Спасибо, что Вы проявили к ней интерес и в хорошем смысле "спровоцировали" его у других. Характерно, что и в Вашем решении и в подходе Короткого В.А. не обошлось без 3D. Я уже выражала свое восхищение Вашим интеллектом. Делаю это еще раз. А доказыавть кому-то что-то - бессмысленно. у всех свои обстоятельства и компетенции. Современные продвинутые студенты лучше нас знают, что им надо. Мы им не соответсвуем (я имею в виду себя и, к сожалению, многих из своих коллег по кафедре).
Хейфец Александр Львович (28 марта 2017 г. 18:39)	Наталья Евгеньевна, за признание моего приоритета благодарен. Мое решение не то, чтобы "не обошлось без 3d", а является в полной мере 3d. И только с помощью этих методов удалось оперативно решить Вашу замечательную задачу. И будем надеяться, что Ваша ошибочная похвала в адрес В.И. Короткого, отрицающего компьютерные 3d методы в учебном курсе, выдана ему в качестве аванса. А.Л. Хейфец
Суфляева Наталья Евгеньевна (28 марта 2017 г. 23:43)	Александр Львович, значит я неправильно поняла фразу Виктора Анатольевича"В целом задача решается переходом от 3D к 2D с последующим поиском точки пересечения прямой линии и кривой второго порядка, наподобие задачи о трансверсали четырех скрещивающихся прямых. Там тоже возникают КВП"? Хотела у него попросить решение. Наверное, я не вправе оценивать мнение о пользе автоматизации в ГГП столь эрудированых людей как он, но мне очевидно (и не только мне, а многим, судя по комментариям), что это отрицание очевидного -получился каламбур. Хочу еще раз подчеркнуть, что задача не моя, а Халдеева И.М. С уважением, Суфляева Н.Е.
Суфляева Наталья Евгеньевна (30 марта 2017 г. 22:59)	Александр Львович, Вам Николай Андреевич подал хорошую мысль: действительно, напишите статью с решением задачи о треугольнике для журнала ГиГ. Не все же читатели журнала участвуют в КГП - пусть тоже ознакомятся. С уважением, Суфляева Н.Е.

Назад Go Back

ГЕОМЕТРИЧЕСКИ ТОЧНАЯ 3D АНИМАЦИЯ КИНЕМАТИЧЕСКИХ ПОВЕРХНОСТЕЙ

Аннотация

Список литературы

Вопросы и комментарии к выступлению:

Александр Владиславович, Геннадий Сергеевич,

Вот такие мои мысли по исчислительной геометрии как экспериментатора, а не теоретика начертательной геометрии.

С уважением. А.Л. Хейфец