ГЕОМЕТРО-ГРАФИЧЕСКИЕ СТУДЕНЧЕСКИЕ ОЛИМПИАДЫ В САНКТ-ПЕТЕРБУРГЕ.
English version

|
Абросимов Сергей Николаевич | (Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова) |
| Глазунов Константин Олегович | (Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова) | |

|
Тихонов-Бугров Дмитрий Евгеньевич | (Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова) |
Аннотация
Рассмотрены вопросы исторического развития и принципов организации олимпиад по начертательной геометрии и компьютерной графике в Санкт-Петербурге. Анализируются конкурсные задания. Высказывается мнение о необходимых тенденциях развития этих важных для повышения качества учебного процесса конкурсов.
Ключевые слова: начертательная геометрия, инженерная графика, компьютерная графика, олимпиада.
В Санкт-Петербурге проводятся две олимпиады, в которых участвуют студенты, проходящие обучение на кафедрах, ведущих графическую подготовку. Это – городская олимпиада по начертательной геометрии и, так называемая, региональная олимпиада по компьютерной графике.
Региональные (или городские) олимпиады, в частности, должны являться отборочным этапом для участия в олимпиадах всероссийских. Крупнейшими и авторитетнейшими всероссийскими олимпиадами, несомненно, являются олимпиады, проводимые Московским Технологическим университетом (МТИ) [3] и Новосибирским техническим университетом.
Открытая всероссийская олимпиада, проводимая МТИ, является уникальным комплексным соревнованием, включающим в себя конкурсные задания по всем разделам графической подготовки: начертательной геометрии, инженерной графике, компьютерной графике. Одновременно проводится интересный конкурс проектов. Участникам предоставляется возможность участвовать в любом из разделов. Подводится и комплексный зачёт.
Кажется, что имеется хорошая возможность проверить: как воспитанники того или иного вуза выглядят на фоне ведущих вузов страны. Однако, складывается странная ситуация: в указанных выше олимпиадах достойно участвуют лишь представители трёх вузов Санкт-Петербурга: Военмеха, Архитектурно-строительного университета, Горного университета. Эти вузы доминируют в городской олимпиаде по начертательной геометрии, доминировали и в региональной олимпиаде по компьютерной графике до момента отказа от участия в ней по причине расхождения с организаторами по вопросам подведения итогов.
Нынешние победители олимпиады по компьютерной графике: ЛЭТИ, ИТМО, ГПУ всероссийские олимпиады игнорируют, а город достойно представляют в них «нелегальные» его представители. Видимо, победители упомянутой олимпиады не разделяют принцип Кубертена: «главное не победа, а участие». Возникает вопрос: можно ли в таком случае считать данную олимпиаду региональной?
В качестве причин неучастия во всероссийских олимпиадах указывают следующие:
- Отсутствие в учебной программе дисциплины «Начертательная геометрия».
- Отсутствие в программе по дисциплине «Инженерная и компьютерная графика» построения моделей сложных сборок.
- Финансовые проблемы для отправки студентов и сопровождающих лиц на олимпиады.
При внимательном рассмотрении программ обучения «Инженерной и компьютерной графике» в тех вузах, где начертательная геометрия не фигурирует в качестве отдельной дисциплины, можно найти раздел, который включает её, мягко выражаясь, элементы. Так в программе, опубликованной на сайте ЛЭТИ, элементы начертательной геометрии занимают одну треть от общего объёма часов.
Организаторы олимпиады по компьютерной графике утверждают, что содержание олимпиадных задач охватывает все дидактические единицы стандартного курса инженерной и компьютерной графики. Однако в олимпиадных заданиях начисто отсутствуют сборки, более сложные, чем соединение крышки с корпусом через прокладку при помощи крепежа. Понятно, почему победители такой олимпиады не слишком стремятся на олимпиаду всероссийскую.
Фактор финансовых проблем отпадает по той причине, что упомянутые выше организаторы всероссийских олимпиад, дают возможность участия по Интернету.
По мнению авторов статьи [4] в олимпиадном мире сложились две ценностные ориентации: научно-содержательная и «спортивная». Это, по их мнению, проявляется в характере заданий, критериях оценки, работе жюри и т.д.
Перманентные дискуссии о месте начертательной геометрии до сих пор не затрагивали олимпиадное движение. Но вот в журнале Геометрия и графика появилась статья [7] в которой утверждается, что: «Вузы, не приступившие к модернизации учебного процесса графических дисциплин, продолжают проводить традиционные олимпиады по начертательной геометрии, где предлагается решать задачи на плоском чертеже. Остальные вузы участвуют в олимпиадах по компьютерной графике и конкурсах асов 3D моделирования».
По логике автора, если вуз проводит упомянутые «традиционные» олимпиады по начертательной геометрии, то он никак не может попасть в передовые «остальные» и заведомо оказывается в компании ретроградов. Таким образом, автор одним махом «пригвоздил» следующие вузы: МВТУ им. Баумана, Московский Технологический университет, Военмех, ГАСУ Санкт-Петербург, Горный университет Санкт-Петербург, ИГЭУ, НИУ МГСУ, БГТУ им. В.Г.Шухова, РГУ нефти и газа им. и.М.Губкина, НГАСУ, ЮГУ, ТИУ, ЮУрГУ, АГТУ, ПНИПУ, СГУПС, СПб ГУТ, УГНТУ, МПУ, НГТУ, УлГТУ – вузы, имеющие богатую историю и проведения олимпиад, и участия в олимпиадах по начертательной геометрии (которые развиваются), что совсем не мешает им успешно участвовать и в олимпиадах по компьютерной графике.
Надо отметить, что упомянутые вузы одними из первых в стране стали преподавать компьютерную (машинную) графику. Так в Военмехе эта дисциплина появилась в учебной программе уже в 1976 году.
Олимпиада по начертательной геометрии была организована в Ленинграде в 1979 году. Городской Совет по научно-техническому творчеству студентов поручил эту работу Военмеху, который успешно с ней справился и курирует её проведение до сих пор. Концепция данной олимпиады, особенности её проведения находятся под постоянным вниманием профессионального сообщества города, объединённого секцией «Геометрия, графика, дизайн» Дома Учёных имени Горького, которую возглавляет д.т.н., профессор Д.В.Волошинов.
Организаторы олимпиады поставили перед собой следующие цели: развитие состязательности в овладении знаниями; демонстрацию применения методов начертательной геометрии на практике; привлечение внимания студентов к разделам курса, рассматриваемым кратко или факультативно; приобщение первокурсников к творчеству [6]. Прикладные задачи превалируют.
Со временем сложилась следующая структура конкурсных заданий:
- Задание, содержащее несколько простых (возможно абстрактных) задач на владение основными методами решения позиционных и метрических задач. Введено пять лет назад по предложению секции Дома Учёных.
- Прикладная задача из области машиностроения, военной техники, архитектуры.
- Задача на применение методов начертательной геометрии при построении ортогонального чертежа изделия.
- Задача на композицию. Появилась десять лет назад. Профессиональное сообщество поддержало идею введения такого задания как средства демонстрации развитости фантазии - необходимого качества инженера-творца. Суть его заключается в том, что по заданным геометрическим образам следует придумать задачу и решить её.
По положению, за организаторами в обязательном порядке остаётся комплексное задание и задание на композицию. Два остальных задания могут быть представлены участниками. В случае одобрения жюри, они включаются в конкурс. При наличии нескольких вариантов заданий, выбор производится по жребию.
Надо отметить, что большинство заданий является следствием решения проблем из инженерной практики преподавателей или носят некий исторический инженерный характер.
Вот несколько примеров. При совместных исследованиях с кафедрой материаловедения (проблемы определения твёрдости материала) возникла следующая задача: пуансон конической формы (рис.1а) вдавливается в металлический лист на глубину 10мм. При этом лист деформируется так, как показано на рисунке. Определите площадь контакта.
Проблема прокладки кабелей в отсеках летательных аппаратов породила ряд задач на оптимальную трассировку, например следующую: проложить кабель между двумя точками на поверхности отсека конической формы (рис.1б) так, чтобы длина кабеля была минимальной. Изобразить трассу на чертеже и определить длину кабеля.
Проектирование кососрезанных сопл и дефлекторных насадок дало основание предложить целый ряд заданий, простейшее из которых связано с построением сечения профилированного сопла проецирующей плоскостью.
Целый спектр задач породила проблема взаимодействия газовых струй с конструкциями разной формы, проблема компоновки оборудования в отсеках летательных аппаратов.
Строительные проблемы отражены в задачах на построение кровель, наличников, рам, законцовок брёвен и т.п.
Столетний юбилей А.И.Солженицына напомнил о том, что Александр Исаевич служил в воинском подразделении, занимавшимся звукопеленгацией. Условие задания следующее: воздушная цель (точка С) засечена двумя звукоулавливателями, находящимися в точках А (направление на источник звука – прямая а) и В (направление – прямая в). В идеале прямые должны пересекаться в точке, где находится источник звука, но в реальности этого, как правило, не происходит. Считают, что вероятное положение источника С – середина отрезка, соединяющего прямые а и в кратчайшим путём. Определить положение точки С (рис.1в).
Вернёмся к задачам и значению олимпиады по начертательной геометрии, объявленным ранее. Опыт длительностью в 39 лет подтверждает правильность поставленных задач. В статье «Олимпиады по начертательной геометрии как катализатор эвристического мышления» [8], авторы чётко классифицируют эффективные функции олимпиад: гуманистические; творческие; мотивация учебной деятельности; организационные; контролирующие; представительские.
Завершая обсуждение олимпиады по начертательной геометрии, обратим внимание на цитату из учебника Монжа: «Очарование, сопровождающее науку, может победить свойственное людям отвращение к напряжению ума и заставить их находить удовольствие в упражнении своего разума, что большинству людей представляется утомительным и скучным занятием». А ведь очень актуально! Не сомневаемся, что все коллеги почувствовали влияние «чёрных зеркал» на интеллектуальный уровень абитуриента. Воистину, революция в части доступа к информации не победила упомянутое отвращение к напряжению ума, а совсем на оборот.
Вот почему очень важно, чтобы олимпиада по компьютерной инженерной графике не носила чисто инструментального характера.
Исходными данными для выполнения конкурсного задания является незавершённый сборочный чертёж и незавершённая спецификация. База заданий содержит порядка 40 вариантов. Конкретный вариант выбирается по жребию. Допускается повторение одного и того же варианта подряд.
Уровень сложности исходного варианта можно оценить по рис. 2а. На наш взгляд такой уровень возможен для участников первого года обучения т.к. источником заданий, в частности, является учебная литература, предназначенная для начального обучения инженерной графике [5]. Предложенные конструкции носят явно упрощённый характер и далеки от реальных. Такие конструкции используются в Военмехе для заданий проектного характера, когда студенты анализируют их недостатки (примитивизм, в частности) и создают модели и чертежи устройств, приближенных к реальным.
Далее конкурсантам предлагается выполнить твёрдотельные модели двух деталей и ассоциативные чертежи. Один чертёж дополняется аксонометрией с вырезом.
Выполнение модели «сборки», состоящей из корпуса и присоединённой к нему детали с помощью крепежа и ассоциативного чертежа этой «сборки» носит чисто инструментальный характер и имеет мало смысла (рис.2б). Требуемые на разрезе справочные размеры соединения не имеет практического значения.
Простановка размеров – особый момент в обучении инженерной графике и, само собой, в олимпиаде. При оценке «причёсанного» ассоциативного чертежа с позиции простановки размеров важен единый подход членов жюри не игнорирующий технологию обработки изделия.
Критерии оценки работ, приведённые в [2], (а их несколько десятков) в большинстве своём весьма размыты и позволяют неоднозначную трактовку.
Таким образом, олимпиада по «Инженерной и компьютерной графике» составляется на базе бакалаврской программы соответствующего курса, построена на простых типовых исходных данных и носит, в основном, инструментальный характер. Побеждает тот, кто за три часа успеет «нарисовать» много изображений. Присущего любым олимпиадам творческого, созидательного характера нет совсем.
Возникшая альтернативная олимпиада «Тотальный чертёж», объединяющая на базе ГУТ вузы, заинтересованные в другом содержании и принципах подведения итогов, за три года приобрела большую популярность. Её содержание, проблемы введения творческих элементов, постоянно обсуждается уже упомянутым профессиональным сообществом.
Резюмируя изложенное, считаем, что городская олимпиада по начертательной геометрии полностью выполняет поставленные задачи, успешно функционирует и развивается, не смотря на многочисленные попытки изъять её из учебного процесса. Надеемся на расширение участников, в частности на возвращение в лоно олимпиады студентов ПГУПС – знаменитого вуза в котором впервые стали преподавать эту замечательную дисциплину.
Что касается олимпиады по инженерной компьютерной графике, на наш взгляд, она нуждается в реорганизации – деления её на две составляющие:
- Олимпиада для вузов с сокращённой программой обучения, готовящих исключительно бакалавров и не претендующих на участие во Всероссийских олимпиадах.
- Олимпиада для вузов машиностроительного профиля, готовящих не только бакалавров, но и специалистов, являющаяся отбором на Всероссийские олимпиады.
Это связано, прежде всего, с различным образовательным уровнем и, как правило, с курсом обучения. Хотя и бывают исключения – есть студенты, обучаемые по программе бакалавров прекрасно справляющиеся с предлагаемыми заданиями по геометрии, и в тоже время хорошо владеющие инструментальными средствами компьютерной графики. Поэтому предложение проведения олимпиад разных уровней (бакалавриат и специалитет) весьма условно. Конечно, успешное выступление на первом или начальном уровне может быть пригласительным билетом для участия на следующем уже более продвинутом.
Уровни олимпиад, прежде всего, должны иметь отличие в содержательной части. А содержательная часть это самая важная составляющая соревновательного процесса. По сути, геометрия является определяющим элементом содержательной части и должна закладывать основы для творческой составляющей.
Обращаясь к опыту проведения олимпиад, следует отметить, что за последние
10 - 15 лет уровень сложности предлагаемых исходных данных значительно увеличился (рис. 3). Это касается, как фактурных геометрических элементов, и их взаимосвязей, так и смыслового наполнения.
Сегодня спектр выполняемых заданий по компьютерной графике достаточно широк и простирается от выполнения 3D модели с ассоциативным чертежом до формирования 3D сборки (и соответствующих 3D моделей деталей, входящих в сборку) (рис.4) и комплекта ассоциативных чертежей. Исходными данными, как правило, являются альбомы чертежей (учебных, конструкторских бюро и производственных предприятий). Более того, в ряде случаев для подтверждения правильно принятых, в соревновательном процессе, конструкторских решений имеет смысл выходить на CNC – технологии (одной из них более доступной, является 3D печать).
Целесообразным, по мнению авторов, является предварительная работа по разработке идеологии и методическим особенностям планируемой олимпиады с выработкой критериев сложности заданий. Важным компонентом исходных данных является поле предполагаемого творчества. Т.е. возможная разработка оригинальных решений по отношению к исходным данным и уровень модификации (количество дополнений и изменений в заданную конструкцию), а также творческая инициатива участников соревновательного процесса с адекватной оценкой их результатов.
Естественно, в этом случае, актуальной является и система оценки с критериями, имеющими базовую (унифицированную) часть и достаточно сложную оценочную часть творческой составляющей, которая должна быть предметом обсуждения например, таким органом, как методический совет при комитете образования или соответствующая секция Дома Учёных.
Особое и важное место занимают предметные олимпиады, имеющие отраслевую направленность, например: ракетно – космическая тематика, авиационная и др.
Хорошим примером, в этом отношении, являются олимпиады проводимые центром ДПО «Интелект» и Ленинградским областным институтом развития образования (ЛОИРО) при участии сотрудников БГТУ «ВОЕНМЕХ» [1], где кроме воссоздания геометрических моделей летательных и космических аппаратов проводятся конкурсы конструкторских разработок .
Инструментальные средства олимпиад, являющиеся только инструментом, не должны быть «жесткими», т. е. участникам предоставляется выбор между 2 – 3-мя пакетами, имеющими наибольшую актуальность в инженерной практике (например, Компас-3D, Solid Works, AutoCAD).
В заключение следует отметить, что олимпиады являются очень серьёзным драйвером образовательного процесса, позволяющие оценит уровень знаний и навыков представителей конкретного учебного заведения, развить дух коллективизма внутри команды и стимулировать более основательную инженерно – техническую подготовку. А организаторам следует посоветовать более вдумчивого и ответственного отношения к предметной, содержательной и организационным сторонам проведения олимпиад среди будущих инженерных специалистов.
Список литературы
- Абросимов С.Н., Пахомова О.Ф., Тихонов-Бугров Д.Е., Уханева В.А. Использование ракетно – космического компонента в графической подготовке в системе школа – вуз. [Электронный ресурс] // Проблемы качества графической подготовки. – 2016. - URL: http://dgng.pstu.ru/conf2016/paper/130 (дата обращения 12.02.19).
- Большаков В.П., Климов В.П., Чагина А.В. Методика подготовки и проведения олимпиад [Текст] / В.П. Большаков, В.П. Климов, А.В. Чагина // Геометрия и графика. – 2017. - №4. – С.83-93.
- Вышнепольский В.И. Функции олимпиад// Геометрия и графика. 2013.- Т.1. №2.
- Гоник И.Л., Юрлова О.В., Текин А.В. Студенческие олимпиады: проблемы и перспективы.// Высшее образование в России. – 2015. - №5.
- Зенюк И.А., Козловский Ю.Г., ПоляничеваА.П.// Машиностроительное черчение с элементами конструирования. Минск. Вышейшая школа. 1977.
- Лызлов А.Н., Ракитская М.В., Тихонов-Бугров Д.Е.// Начертательная геометрия. Задачи и решения. Спб. Лань. 2011.
- Поликарпов В.Ю. Содержание вузовского курса начертательной геометрии в эпоху третьей промышленной революции.// Геометрия и графика. 2018. Т.6. Вып.3.
- Сальков Н.А., Вышепольский В.И., Аристов В.М., Куликов В.П. Олимпиады по начертательной геометрии как катализатор эвристического мышления.// Геометрия и графика. 2017. Т.5. Вып.2.
Рисунки к докладу
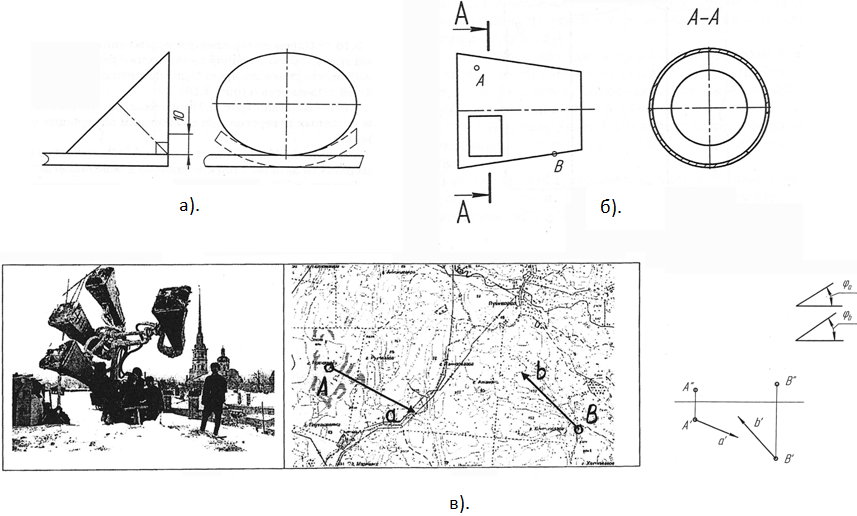
Рис. 1 Примеры прикладных задач геометрического характера
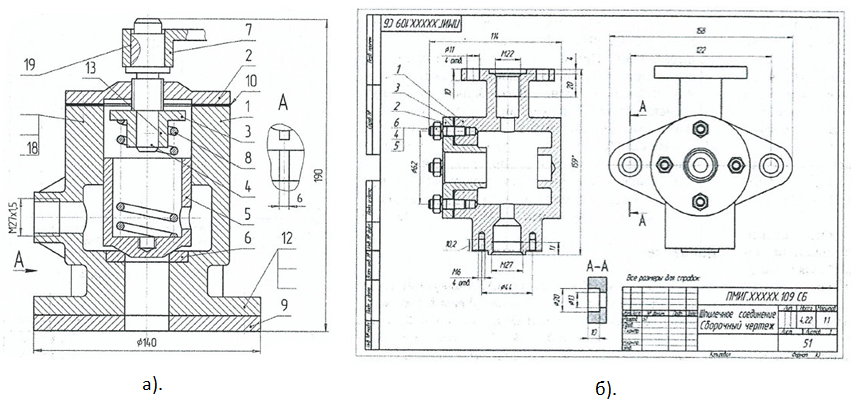
Рис. 2 Исходные данные [2].
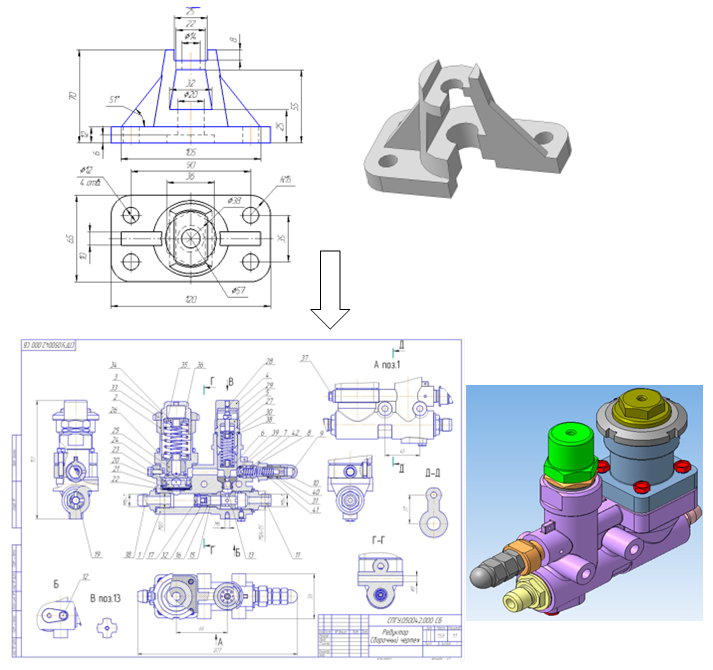
Рис. 3 Уровень сложности исходных данных в сравнении с 10-15 летней давностью.
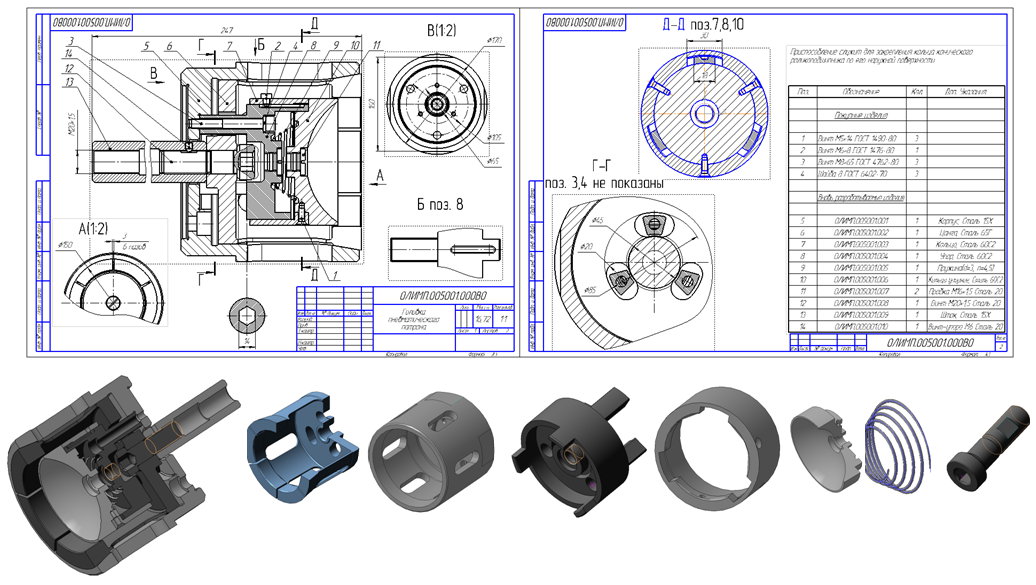
Рис. 4 . Исходные данные а). и выполненные по ним 3D модели изделия б).
Вопросы и комментарии к выступлению:

Сальков Николай Андреевич (3 марта 2019 г. 1:22) |
Здравствуйте, Дмитрий Евгеньевич! И остальные соавторы! Как всегда, глубина Вашего расследования впечатляет! Те граждане, которые думают, что проведение олимпиад - это "легкий ветерок", прочитав Ваше исследование, смогут сообразить, что не так все просто в "королевстве" их заблуждений. С удовольствием прочитал Ваши рассуждения. С уважением, Н. Сальков |

Тихонов-Бугров Дмитрий Евгеньевич (9 марта 2019 г. 23:34) |
Большое спасибо, Николай Андреевич! Успехов Вам в борьбе с "королевством заблуждений". С уважением, Тихонов-Бугров. |
|
Кудревич Аркадий Иванович (14 марта 2019 г. 18:09) |
Считаю, что проведение Олимпиады позволяет повысить интерес студентов не только к общеобразовательным, но и техническим наукам, что повышает в итоге уровень знаний инженра в целом. |
|
Шкварцов Виктор Вадимович (14 марта 2019 г. 21:54) |
В педагогике, в последние годы, все больше внимания уделяется развитию творческого подхода студента при решении инженерных задач. Творческий подход при решении подобных задач, опирается на внедрение компьютерных технологий и выбор требуемого решения из множества возможных альтернативных решений. В этом смысле, Олимпиады расширяют подготовку студента, повышают интерес к “цифре” и качество профессиональной подготовки. |
|
Дюмин Владимир Андреевич (18 марта 2019 г. 10:28) |
В течение ряда лет я принимал участие в проведение городской олимпиады по начертательной геометрии. К моему большому сожалению отмечается неумение некоторых участников олимпиады решать простейшие задачи, например, построение фронтальной проекции отрезка, если известна его горизонтальная проекция и угол наклона к горизонтальной плоскости проекций. Еще - определение расстояния между скрещивающимися прямыми. С уважением Дюмин В.А.
|

Бойков Алексей Александрович (28 марта 2019 г. 0:37) |
Здравствуйте, Дмитрий Евгеньевич, Сергей Николаевич и Константин Олегович! Большое спасибо за подробный и содержательный анализ серьезного вопроса. Есть над чем подумать. с уважением, А. Бойков |

Тихонов-Бугров Дмитрий Евгеньевич (28 марта 2019 г. 14:48) |
Большое спасибо, Алексей Александрович! Успехов Вам в преподавательской и научной работе. Ждём диссертационных успехов. С уважением, Тихонов-Бугров. |
Назад Go Back