ЛИНЕЙНАЯ КОНГРУЭНЦИЯ С МНИМЫМИ ОСЯМИ
English version

|
Короткий Виктор Анатольевич | (Южно-уральский государственный университет (Национальный Исследовательский Университет)) |
Аннотация
Решена задача построения эллиптической линейной конгруэнции, заданной четырьмя скрещивающимися прямыми. Предложен алгоритм перехода от конгруэнции, заданной че-тырьмя скрещивающимися прямыми, к тождественной конгруэнции, заданной двумя кол-линеарными полями. Рассмотрен пример выделения линейчатой алгебраической поверхно-сти четвертого порядка из эллиптической линейной конгруэнции.
Ключевые слова: Эллиптическая линейная конгруэнция, мнимые сопряженные направляющие, эллиптиче-ская инволюция, коллинеарные поля.
1. Введение
Один из методов конструирования линейчатых алгебраических поверхностей основан на выделении их из линейной конгруэнции K(1,1) с осями m, n, посредством погружения в K(1,1) алгебраической кривой ek порядка k в качестве третьей направляющей [7, 8, 10]. В частности, если k=2, получаем поверхность четвертого порядка. Если поверхность выделяется из гиперболической конгруэнции (оси m, n – вещественные), то получаем клиновидную двулистную поверхность, прямолинейные образующие которой определяются обычными способами начертательной геометрии (рис. 1).
Существует пучок плоскостей, пересекающих эту поверхность по кривым второго порядка. Ось пучка определяется на основе следующей теоремы [13].
Теорема Reye. Пусть линейчатая поверхность T задана направляющей кривой ek порядка k и двумя вещественными (или мнимыми сопряженными) скрещивающимися прямолинейными направляющими m, n, пересекающимися с плоскостью кривой ek в вещественных (или мнимых сопряженных) точках M, N. Тогда прямая MN является осью пучка плоскостей, пересекающих поверхность T по алгебраическим кривым порядка k.
Доказательство. Прямая MN пересекает направляющую кривую ek в двух точках (действительных, совпавших или мнимых сопряженных), а также пересекает прямолинейные направляющие m, n, следовательно, MN представляет собой две совпавшие образующие поверхности T. Линейчатая поверхность T – алгебраическая поверхность порядка k+2 [3, стр. 86], в сечении которой произвольной плоскостью пучка с осью MN получаем кривую, распавшуюся на считаемую дважды прямую MN и на кривую порядка k. Теорема доказана.
Рассмотрим двухосевую поверхность Θ4, представленную на рис. 1. Поверхность выделена из конгруэнции (m, n) посредством погружения в нее окружности r2. Отличительная особенность поверхности состоит в том, что плоскость R окружности r2 параллельна осям m, n, поэтому MN – несобственная прямая плоскости R. Согласно теореме Reye, в сечении поверхности Θ4 плоскостями пучка с несобственной осью MN получаем кривые второго порядка. Заметим, что такая поверхность может быть задана как поверхность с пропорциональной разбивкой хорд двух любых конических сечений поверхности [3, стр. 89], [11].
Теорема Reye справедлива как для вещественных, так и для мнимых сопряженных направляющих m, n. Конгруэнцию K(1, 1) с мнимыми осями называют эллиптической линейной конгруэнцией (ЭЛК) [9]. Через произвольную точку пространства проходит единственный луч ЭЛК, пересекающий мнимые оси m, n. Очевидно, построить этот луч “лобовым способом”, с помощью обычных средств начертательной геометрии, не удается.
Графический алгоритм решения основан на теореме Reye. Переход от графического решения к аналитическому на любом этапе построений выполняется на основе теоремы Гирша, устанавливающей взаимно-однозначное соответствие между действительными координатами x0, y0, xL, yL маркера {OL}, изображающего мнимые точки M, N, и комплексными декартовыми координатами этих точек [2]. В теореме утверждается, что между координатами x0, y0 центра O эллиптической инволюции σ на прямой l, координатами xL, yL точки Лагерра L, из которой инволюция σ проецируется ортогональным пучком, и комплексными координатами A(x=a+jb, y=c+jd), B(x=a-jb, y=c-jd) мнимых двойных точек A~B инволюции σ установлено соответствие: a=x0, b=y0-yL, c=y0, d=xL-x0.
2. Постановка задачи
Известны различные способы задания конгруэнции K(1, 1). В частности, четыре попарно скрещивающиеся прямые a, b, c, d с мнимыми трансверсалями определяют единственную ЭЛК (рис. 2, а). Естественным образом формулируется задача: через произвольную точку E пространства R3 провести прямую e, включенную в эту конгруэнцию. Иными словами, надо составить алгоритм построения прямой, проходящей через данную точку E и пересекающей мнимые трансверсали скрещивающихся прямых a, b, c, d.
3. Алгоритм построения прямой, пересекающей мнимые оси ЭЛК, заданной четырьмя скрещивающимися прямыми
Шаг 1. Через данную точку E проводим произвольную плоскость П и отмечаем точки A, B, C, D пересечения прямых a, b, c, d с плоскостью П (см. рис. 2, а).
Шаг 2. Взяв какую-либо тройку прямых (например, a, b, c), выделяем заданную этими прямыми квадрику Ф(abc), и находим ее сечение плоскостью П. Получаем конику c2=Ф∩П (рис. 2, б). Вычерчивание непрерывного конического сечения выполняется с использованием программного средства “Универсальный компьютерный коникограф” [4, 6].
Примечание к шагу 2. Квадрика Ф состоит из двух полуквадрик Ф1 и Ф2. Полуквадрика Ф1 образована семейством прямых (a, b, c,…), а Ф2 – прямыми, пересекающими это семейство. В частности, Ф2 содержит мнимые образующие m, n, проходящие через мнимые точки U, V пересечения прямой d с квадрикой Ф. Мнимые прямые m, n являются осями эллиптической конгруэнции, заданной прямыми a, b, c, d. Поскольку мнимые прямые m, n инцидентны квадрике Ф, то мнимые сопряженные точки M, N пересечения этих прямых с плоскостью П инцидентны конике c2.
Шаг 3. Взяв другую тройку прямых (например, a, b, d), получаем квадрику Г, состоящую из двух полуквадрик Г1(abd) и Г2. Полуквадрика Г2 образована семейством прямых, пересекающих образующие a, b, d полуквадрики Г1. В семейство Г2 входят мнимые прямые m, n, поэтому мнимые точки M, N пересечения прямых m, n с плоскостью П инцидентны коническому сечению d2=Г∩П. Коника d2 вычерчивается с помощью программного средства “Универсальный компьютерный коникограф” (см. рис. 2, б).
Примечание к шагу 3. Мнимые сопряженные точки M, N пересечения мнимых осей m, n с плоскостью П являются второй парой точек пересечения конических сечений c2 и d2, пересекающихся в паре действительных точек A, B (см. рис. 2, б).
Шаг 4. Находим прямую l, проходящую через M, N. Коники c2, d2 устанавливают на l одну и ту же эллиптическую инволюцию σ с мнимыми двойными точками M, N. Находим центр O инволюции σ, и точку Лагерра L, из которой попарно соответственные точки инволюции σ проецируются парами взаимно перпендикулярных прямых. Получаем маркер {OL}, изображающий на плоскости П мнимые точки M, N.
Примечание к шагу 4. Построение прямой l, проходящей через мнимые точки M, N пересечения двух коник c2, d2, имеющих две общие действительные точки A, B, выполняется “одной линейкой” [12]. Построение маркера {OL}, изображающего точки M, N, выполняется линейкой и циркулем [1, 5]. Для проверки точности построения маркера найдены поляры pC, pD произвольно отмеченной на l точки P (в поляритетах c2, d2). Поляры пересекаются в точке P' на прямой l. Точки P и P' проецируются из точки Лагерра L взаимно перпендикулярными лучами, что подтверждает точность построения маркера (см. рис. 2, б).
Шаг 5. Предположим, что задача решена, то есть искомая прямая e построена (напомним, что прямая e должна проходить через точку E и пересекать мнимые оси m, n). Вводим в рассмотрение квадрику H, содержащую полуквадрики H1(abe) и H2. Полуквадрика H2 образована прямыми, пересекающими прямые a, b, e, следовательно, в состав полуквадрики H2 входят мнимые прямые m, n. Поэтому сечение e2 квадрики H плоскостью П должно быть инцидентно точкам M, N. Таким образом, сечение e2 вполне определено тремя действительными точками A, B, E и двумя мнимыми точками M, N, заданными маркером {OL}.
Примечание к шагу 5. Коника e2(ABEMN) начерчена в соответствии с алгоритмом, изложенным в [1, 5]. Для проверки точности построения коники e2 выполнено вспомогательное построение: на прямой l, проходящей через мнимые точки M, N, отмечена произвольная точка P и найдена ее поляра pe в поляритете e2. Эта поляра пересекает прямую l в точке P'. Точки P и P', соответственные в эллиптической инволюции, установленной коникой e2 на прямой l, проецируются из точки Лагерра L ортогональными лучами, что подтверждает точность построения коники e2.
Шаг 6. Квадрика H(abe) вполне определена коническим сечением e2 и двумя образующими a, b. Выделение из этой квадрики искомой образующей e, проходящей через точку E на квадрике, выполняется известными из начертательной геометрии способами. Задача решена.
4. Переход от ЭЛП, заданной четырьмя скрещивающимися прямыми, к тождественной ЭЛП, заданной двумя коллинеарными полями
Указание ЭЛП посредством четырех скрещивающихся прямых вызывает затруднения при конструктивном построении прямых, включенных в эту ЭЛП. Более удобный в конструктивном плане способ основан на задании ЭЛП плоскими коллинеарными полями П↔П' со слабоинвариантной прямой l=П∩П'. Рассмотрим алгоритм перехода.
1. Отмечаем точки A, B, C, D пересечения заданных прямых a, b, c, d с произвольной плоскостью П. Напомним, что прямые a, b, c, d имеют две мнимые сопряженные трансверсали m, n.
2. Выполняя шаги 2-4 алгоритма (см. п. 3), находим прямую l, проходящую через мнимые точки M, N пересечения прямых m, n с плоскостью П, а также выполняем построение маркера {OL}, изображающего точки M, N.
3. Через прямую l проводим произвольную плоскость П', не совпадающую с П. Отмечаем на П' точки A', B', C', D' пересечения прямых a, b, c, d с плоскостью П'. Преобразование П(A, B, C, D)↔П'(A', B', C', D') есть коллинеация φ с мнимыми двойными точками M=M', N=N' на самосоответственной прямой l=l'. Коллинеарность полей П, П' следует из теоремы Reye при k=1, а также может быть доказана элементарными средствами начертательной геометрии.
4. Коллинеация φ(П↔П') задается четырьмя парами соответственных точек, из которых две пары M=M' и N=N' зафиксированы маркером {OL}. Поэтому для полного определения коллинеации φ достаточно отметить на плоскостях П, П' только две пары соответственных точек, например, A-A' и B-B'. Коллинеация φ индуцирует на прямой l=l' проективное преобразование φl с двумя парами мнимых двойных точек {OL}. Третья пара соответственных в φl точек определяется на пересечении прямых AB и A'B' с прямой l=l'. Три пары соответственных точек вполне определяют преобразование φl. Построение соответственных точек в этом преобразовании выполняется с помощью вспомогательной окружности r произвольного радиуса, лежащей в плоскости П или П', и проходящей через точки {OL}. Согласно [2], окружность r ортогональна окружности с центром O и радиусом OL. Проективные пучки с центрами на r высекают на l=l' пары соответственных в φl точек, что, в свою очередь, позволяет находить точки, соответственные в коллинеации φ(П↔П'). Семейство прямых, соединяющих пары точек, соответственных в φ, есть коллинеация, тождественная коллинеации, заданной прямыми a, b, c, d.
Примечание. Алгоритм перехода от ЭЛП (a, b, c, d) к ЭЛП (φ) может быть составлен на основе теоремы: коллинеация φ(П↔П') со слабоинвариантной прямой l=П∩П' вполне определена указанием двух коник k, k' и парой соответственных точек на l [8]. При этом, очевидно, сохраняется необходимость построения прямой l.
5. Пример (линейчатая поверхность 4 порядка, выделенная из ЭЛП)
Пусть линейчатая алгебраическая поверхность четвертого порядка задана коническим сечением e2, лежащим в верхней грани куба (рис. 3), и четырьмя скрещивающимися образующими a, b, c, f, не имеющими действительных трансверсалей. Требуется построить каркас поверхности.
Полагая, что искомая поверхность выделяется из ЭЛП, заданной прямыми a, b, c, f, отмечаем на e2 произвольную точку Q и выполняем действия 1-6 алгоритма (см. п. 3). Получаем дополнительную (пятую) образующую q искомой поверхности, а также прямую l, лежащую в плоскости направляющей e2 и пересекающую мнимые оси конгруэнции (a, b, c, f). Согласно теореме Reye, произвольная плоскость, проходящая через l, пересекает искомую поверхность по коническому сечению. Множество таких сечений и множество прямолинейных направляющих образует неограниченно пополняемый каркас поверхности (см. рис. 3). Для построения сечения поверхности произвольной плоскостью пучка l необходимо отметить в этой плоскости пять точек пересечения с пятью образующими a, b, c, f, q, после чего с помощью программного модуля “Универсальный компьютерный коникограф” начертить коническое сечение “по пяти точкам”.
Заключение
Как в алгебре, так и в геометрии, мнимые элементы являются неотъемлемым атрибутом любых действий с алгебраическими многообразиями. Участие мнимых линейных элементов в геометрических построениях так же необходимо и естественно, как участие комплексных чисел в алгебраических преобразованиях. Это сознавали и практически использовали выдающиеся геометры 19 века. Нет никаких сомнений, что простой и совершенно очевидный алгоритм 1-6, изложенный в п. 3, давно известен. Компьютерная графика всего лишь позволяет выполнить точную конструктивную реализацию этого алгоритма. Некоторый скепсис по отношению к мнимым геометрическим фигурам у преподавателей ГГП, видимо, имеет ту же природу, что и сомнения ученика 9 класса, который на уроке алгебры не желает признавать комплексные числа. При операциях с алгебраическими объектами алгебра и геометрия “идут рядом”. Например, теорема Гирша позволяет установить взаимно-однозначное соответствие между комплексными декартовыми координатами мнимых точек и вещественными координатами маркера, изображающего эти точки [2], а алгоритмы построения коники по любому набору пяти линейных элементов (точек и касательных) одинаково хорошо работают как для действительных элементов, так и для наборов с участием мнимых сопряженных элементов [1, 5].
Список литературы
Рисунки к докладу
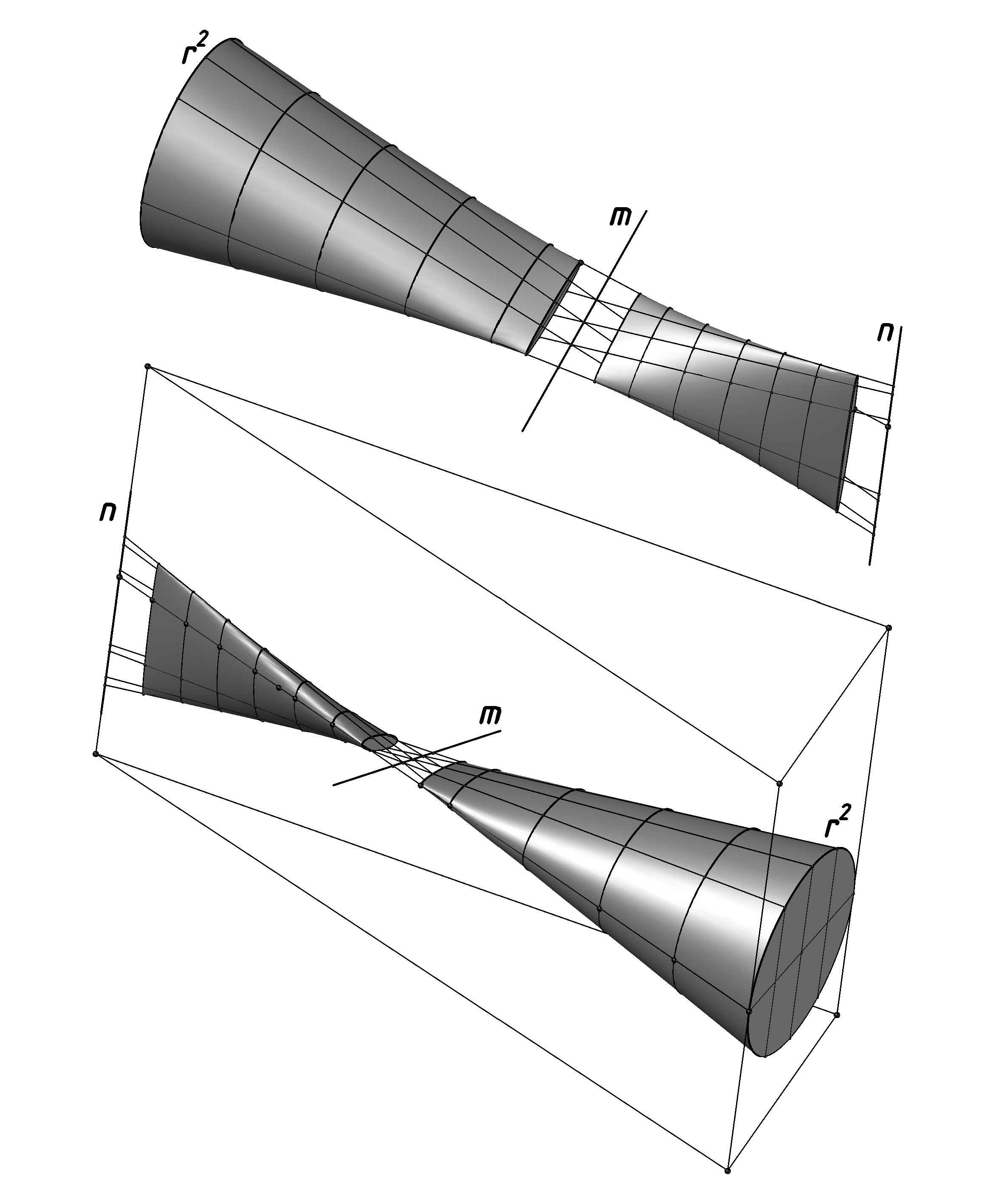
Рис. 1 Двухосевая поверхность
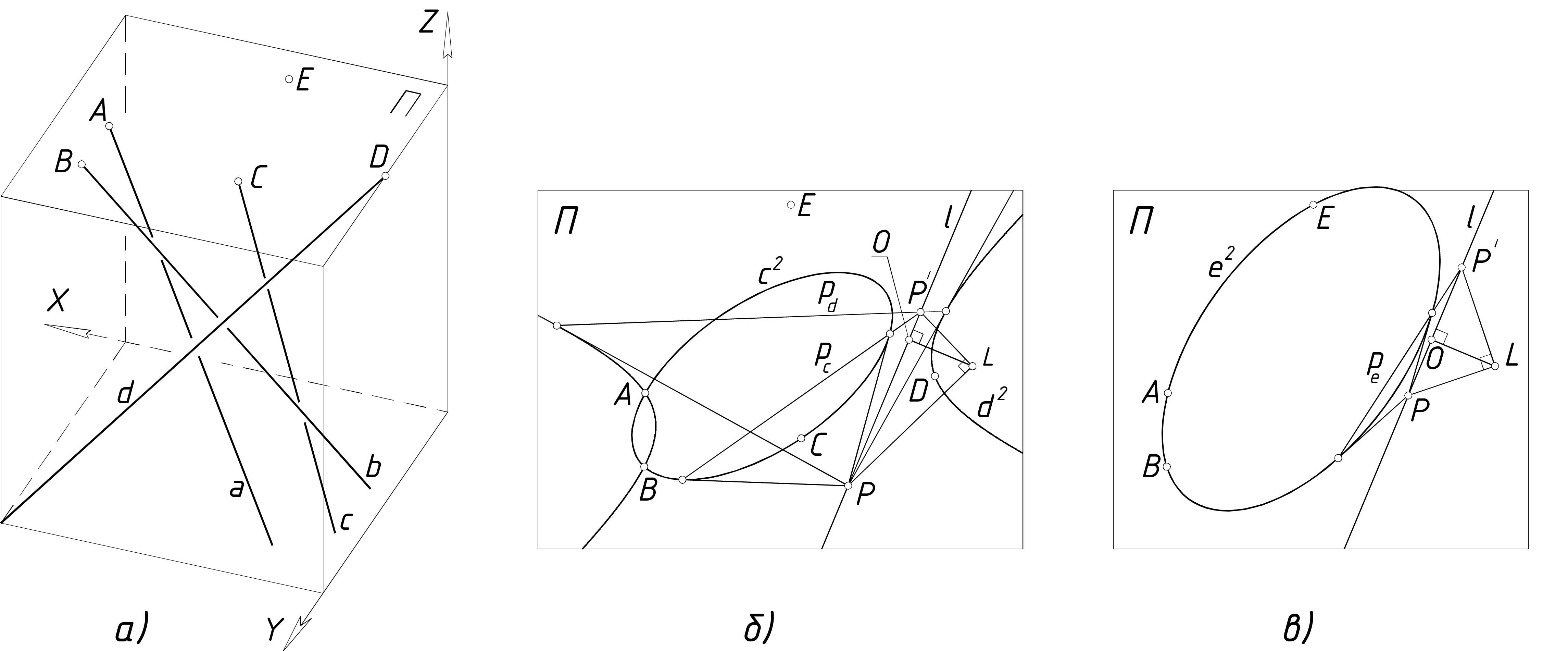
Рис. 2 К алгоритму построения ЭЛП, заданной четырьмя скрещивающимися прямыми: а - исходные данные; б - построение маркера OL, изображающего мнимые точки M, N; в - построение коники через три действительные точки A, B, E и две мнимые точки, заданные маркером OL
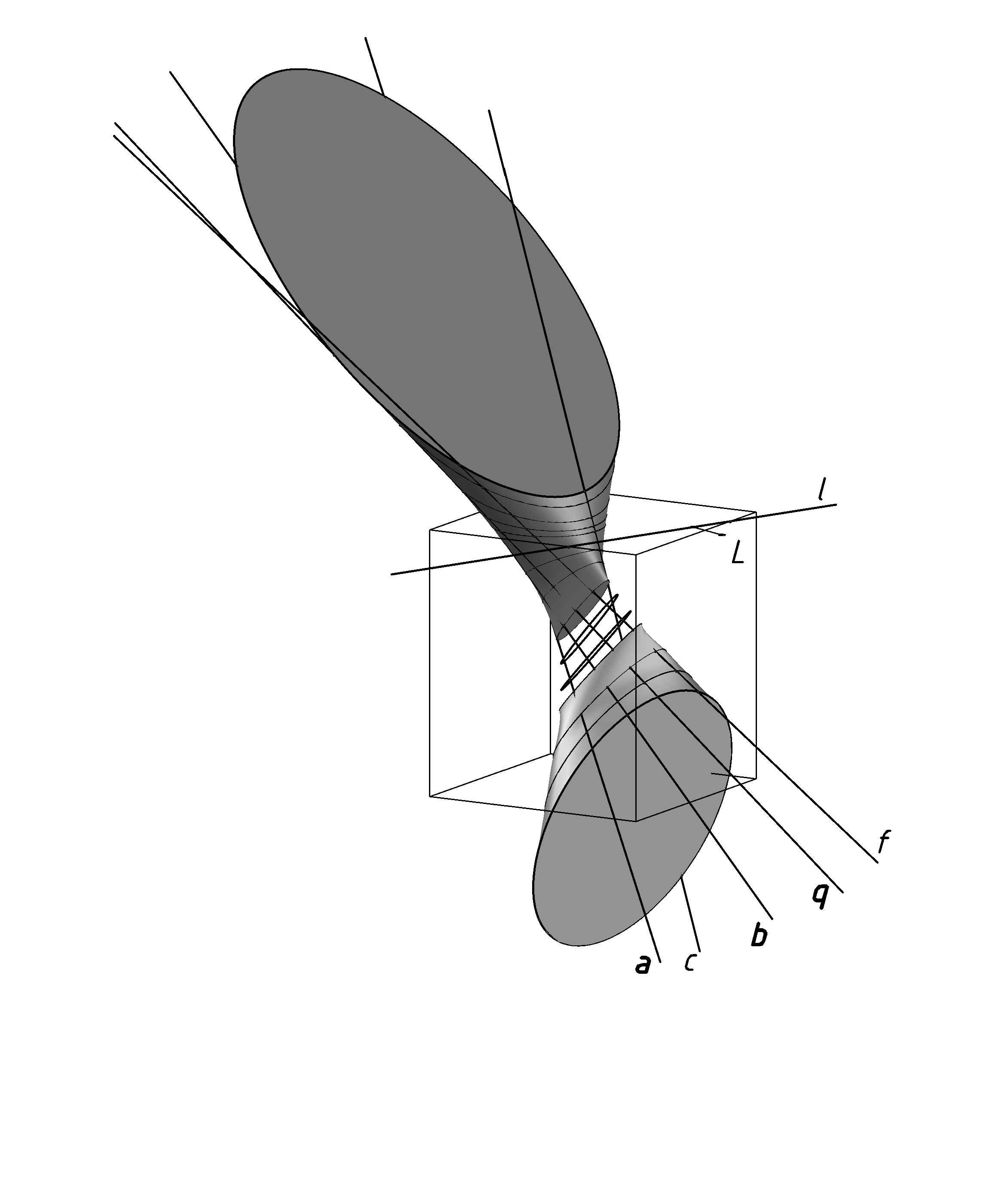
Рис. 3 Алгебраическая поверхность четвертого порядка, выделенная из ЭЛП, заданной скрещивающимися прямыми a, b, c, q
Вопросы и комментарии к выступлению:

Кокарева Яна Андреевна (11 марта 2019 г. 22:41) |
Уважаемый Виктор Анатольевич, спасибо за доклад! Было интересно прочитать "родную" тематику в Вашей интерпретации. Если Вас заинтересуют мои варианты построения линейных конгруэнций с мнимыми элементами (гиперболическая конгруэнция с одной мнимой директрисой и параболическая конгруэнция с мнимой директрисой), то могу перевести свой автореферат на русский ))) А если серьезно, то помимо Обуховой и Подгорного, я думаю, честно было бы упоминуть их ученика и моего учителя Скидана И.А., который много времени уделил изучению конгруэнций. А статья хорошая. Искреннее спасибо! С уважением, Кокарева Я.А. |

Короткий Виктор Анатольевич (11 марта 2019 г. 23:16) |
Яна Андреевна, будьте добры пояснить, что такое линейная гиперб конгруэнция с одной мнимой осью? Мнимые сопряженные прямые неразлучны, как полюсы магнита. У линейной дуальной конгруэнции могут быть 2 действительные (ГЛК) или 2 мнимые сопряженные (ЭЛК) или 2 совпавшие (ПЛК) оси. Заранее благодарю за ответ. С уважением, В. Короткий |
Назад Go Back