

|
Вышнепольский Владимир Игоревич | (Московский государственный университет тонких химических технологий имени М.В. Ломоносова) |
В работе рассмотрена задача о построении точек пересечении окружности и эллиптического конуса. Приведено более точное решение этой задачи.
В одной из статей секции «Теоритические исследования в области прикладной геометрии и практического решения задач инженерной графики» рассмотрена задача об определение точек пересечения окружности с эллиптическим конусом. Предложим другое решение этой задачи, чуть более точное.
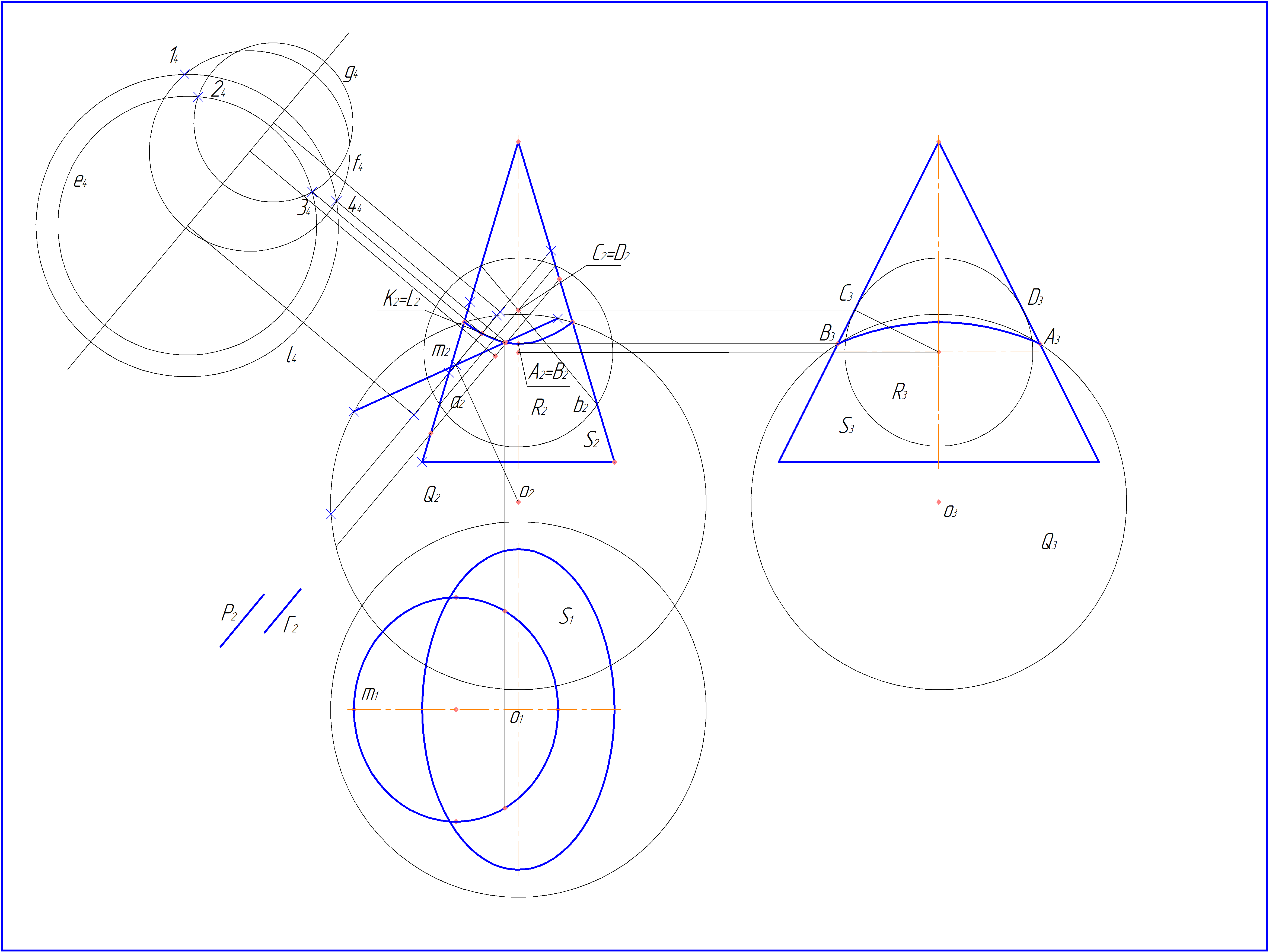
Дано: окружность m, плоскость окружности перпендикулярна p2 и эллиптический конус S.
Решение. Точки пересечения окружности m и конуса S можно построить как точки пресечения окружности m с линией пересечения сферы Q и конуса S. Задача будет решаться проще, если сфера Q окажется соосна конусу.
Точки линии пересечения сферы Q и конуса S строятся с помощью плоскостей посредников рассекающих и сферу, и конус по окружностям. Для того чтобы провести такие плоскости найдены круговые сечения конуса S. Для этого построена проекции конуса на p3 S3 и сфера R имеющая с конусом S в двух их общих точках D и C общие касательные плоскости.
По теореме о двойном соприкосновении конус S и сфера R пересекаются по двум окружностям a и b, секущие плоскости Г и P будут рассекать и конус и сферу по окружностям g и е, f и l, которые построены на плоскость проекций p4. Пересечение окружностей g и е, f и l дает точки 2,3 и 1,4 принадлежащие линия пересечения d конуса S и сферы Q.
Необходимо особо подчеркнуть, что предложенным методом линия пресечения конуса S и сферы Q строятся совершенно точно, без лекальных кривых. Таким образом, точность решения задачи существенно повышается. Ответом задачи являются точки пересечения линий m и d - K и C.

Хейфец Александр Львович (20 марта 2015 г. 22:02) |
Владимир Игоревич. Позвольте высказать замечания по представленной задаче. Линия пересечения эллиптического конуса S и вспомогательной сферы Q – пространственная кривая 4-ого порядка. Ее фронтальная проекция при совмещении осей S и Q – ветка гиперболы. В начертательной геометрии точное построение гиперболы невозможно, можно находить только отдельные ее точки. Хотя Вы пишете, что эта кривая построена точно, это не так. Ее точки – найдены точно в связи построением круговых сечений конуса. Сама гипербола – приближенно. В целом, Ваше решение весьма приближенное, причем, приближенное в принципе, как все решения НГ для подобных задач. Если нет общей симметрии S и Q, то и в проекции будет кривая 4-ого порядка, также воспроизводимая приближенно по точкам. Кроме того, если плоскость заданной окружности не проецирующая, то двойного соприкосновения S и R не будет, и решение методами НГ получится еще менее точным. Теперь современное геометрически точное элементарное решение в 3d графическом пакете: построить эллиптический конус, построить его сечение плоскостью заданной окружности – в сечении получим конику. Осталось поставить маркеры точек в пересечении заданной окружности и коники и измерить координаты. В общем случае получим 4-х точки (для Вашего примера - две точки, поскольку коника - эллипс). Координаты будут определены с погрешностью не более 10-6 (одна миллионная). Причем, решение будет для любого положения окружности (конечно, если пересечение есть). Можно ли считать 3d решение точным - вопрос непростой. Ответ на него зависит от того, что ситать геометрически точным решением. В целом, Ваше решение соответствует направлению задач номинации НГ на Вашей олимпиаде, о несостоятельности которых я говорил в своем докладе и замену которых на современные задачи я Вам предложил. Ранее, в дискуссии на близкую тему на данной конференции было высказано по такому же поводу, что зато методами НГ студенты получат решение своими руками, а не нажатием кнопок. Так что лучше, получить неточное решение своими руками, или точное решение (причем быстро, красиво) на компьютере 3d? Готов продолжить обсуждение. С уважением. А.Л. Хейфец |

Сальков Николай Андреевич (20 марта 2015 г. 22:56) |
Александр Львович! Да, гипербола. И, точно определив 5 точек этой гиперболы, мы можем вполне точно (!) построить ее посредством законов проективной геометрии. Александр Львович, Вы сами говорили, что совершенно неизвестно, что именно зашито в AutoCAD'е. Представленный чертеж был выполнен при помощи КОМПАСа. Отечественного продукта. Тут мы можем, составив программу, точно найти миллион точек на 1 мм длины дуги. И тогда точность построения должна удовлетворить всех. Денис Вячеслававич Волошинов как-то писал, что при переходе на цифровую обработку информации, теряется часть этой информации, поскольку, хотя разрядная сетка регистров в процессорах вычислительных машин и может быть сделана очень большой, но все же не бесконечной. Следовательно, абсолютной (геометрической) точности на компьютере добиться в принципе невозможно. Мы можем лишь говорить о той ошибке в вычислениях, которая нас удовлетворяет - и не более того. Поэтому и в так называемой 3d-интерпретации решения вопрос о точности решения может быть закрыт - они все, в действительности, неточные. На компьютере невозможно добиться геометрически точного решения только потому, что компьютер - инструмент, а не наука. И как каждый инструмент имеет свою погрешность. Геометрия же - наука абстрактная, а потому - точная. В журнале ГиГ (том.2, №1, 2014) проф. Д.В. Волошинов пишет: "Ситуация, которую мы наблюдаем, - это ошибочное причисление науки, системы моделирования, к конкретному прикладному делу, что в корне неверно". Ну не надо путать науку с инструментом! С уважением, Сальков. |

Бойков Алексей Александрович (21 марта 2015 г. 12:58) |
Андрей Николаевич! Гиперболу можно преобразовать в эллипс или окружность, подобрав подходящий конус или центр гомологии, и тогда решие найдется точно. С параболой получается. С уважением, А.А. Бойков |

Хейфец Александр Львович (21 марта 2015 г. 18:09) |
Алексей Александрович, как отмечено, гипербола здесь получается лишь в частном случае, а в общем - проекция будет кривой 4-ого порядка и ее не возмешь проективной геометрией. И в целом, коллеги, что нужно в этой простой задаче и аналогичной ей: "результат или процесс поиска". Если результат - то включайте 3d редактор (как сказано выше) , если процесс - то ищите.... С уважением. |