



|
Козлова Ирина Алексеевна | (Астраханский государственный технический университет) |

|
Славин Борис Матвеевич | (Астраханский государственный технический университет) |

|
Харах Матвей Максимович | (Астраханский государственный технический университет) |
Рассмотрено построение линии пересечения некоторых сложных поверхностей между собой и построение точек пересечения кривых линий с этими поверхностями в КОМПАС-график
Кривые поверхности широко применяются в науке и технике. Построение линии пересечения поверхностей рассмотрено в многочисленных научных статьях, диссертациях. Точное построение линий пересечения поверхностей находит широкое практическое применение при проектировании конструкций из листового материала, для изготовления которых необходимо строить развертки. В этом случае точность изготовления элементов конструкций в значительной степени зависит от точности построения проекций линии пересечения поверхностей на комплексном чертеже.
Построение линии пересечения поверхностей путем применения поверхностей-посредников пригодно для ограниченного числа пар линейчатых поверхностей и поверхностей вращения. Применение этого способа для более сложных поверхностей или поверхностей второго порядка общего вида приводит к громоздким построениям, сопровождающимся вычерчиванием множества лекальных кривых. Это значительно снижает точность построений. И здесь на помощь приходит вычислительная техника с графическим редактором КОМПАС-График. Далее рассматривается построение линии пересечения некоторых сложных поверхностей между собой и построение точек пересечения кривой линии с этими поверхностями.
1. Построение линии пересечения эллиптического конуса и трехосного эллипсоида с помощью графического редактора Компас-График Задача решается методом вспомогательных секущих плоскостей (рис. 1). Горизонтальные плоскости уровня пересекают данные поверхности по эллипсам, которые в Компас-График легко строятся по двум осям. Точки пересечения этих эллипсов и являются искомыми точками, принадлежащими линии пересечения.
В командах Компас-График это выглядит следующим образом. Построение очерков эллиптического конуса в Компас-График и эллипсоида вращения выполняем на инструментальной панели Геометрия. Горизонтальную проекцию этих фигур вычерчиваем командой Эллипс с указанием осей. Фронтальная проекция конуса с учетом линий связи будет задана образующими эллиптического конуса в виде отрезков, выполненных стилем линии Основная, а ось – штрихпунктирная линия, которая задается в окне Стиль линии на Панели свойств. Вспомогательные секущие плоскости проводим в виде тонкой линии, надписи точек (опорных и промежуточных) выполняем командой Ввод текста на Инструментальной панели Обозначение. Подстрочные индексы выполняем командой Вставкаndash; Индекс малой величины (или как дробь) с нажатием клавиши darr; для нанесения нижнего подстрочного индекса.
По аналогии могут быть построены линии пересечения различных сочетаний сложных поверхностей 2-го порядка, таких, как трехосный эллипсоид, эллиптический цилиндр, параболоид эллиптический, однополостный и двухполостный гиперболоид общего вида.
2. Построение точек пересечения кривой линии с эллиптическим конусом В качестве кривой линии берем окружность m (рисунок 2), расположенную на сфере. Горизонтальная проекция этой окружности есть эллипс m1. Алгоритм построения точек пересечения линии с кривой поверхностью повторяет алгоритм пересечения прямой линии с кривой поверхностью. В нашем случае проводим через кривую m цилиндрическую поверхность и находим линию пересечения ее с эллиптическим конусом. Задачу решаем также методом секущих плоскостей как в предыдущей задаче. Точки пересечения этой линии с окружностью будут искомыми точками. В командах Компас-График построения выполняем аналогично вышеизложенному.
3. Построение точек пересечения эллипса с трехосным эллипсоидом В качестве эллипса (рис. 3) возьмем линию пересечения конуса вращения с фронтально-проецирующей плоскостью. Алгоритм построения: проводим через эллипс эллиптический цилиндр и строим линию пересечения его с трехосным эллипсоидом (см. п.1.). точки пересечения этой линии с эллипсом искомые.
По аналогии могут быть построены линии пересечения различных сочетаний сложных поверхностей 2-ого порядка таких, как 3-х осный эллипсоид, эллиптический цилиндр, эллиптический параболоид, однополостный и 2-х полостный гиперболоиды общего вида. Данный материал может быть положен в основу методического пособия и замены типового задания на пересечение поверхностей вращения на более сложное задание, выполняемое на компьютере с помощью графических редакторов Компас-График или AutoCAD. Дальнейшим продолжением работы может быть построение линии пересечения поверхностей путем создания их 3D-моделей.
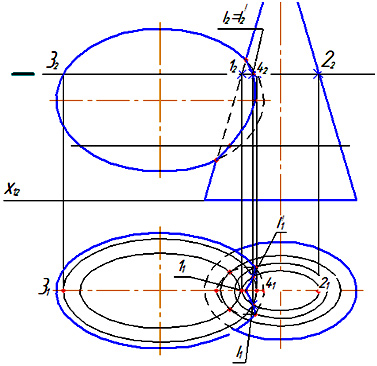
Построения линии пересечения эллиптического конуса и трехосного эллипсоида
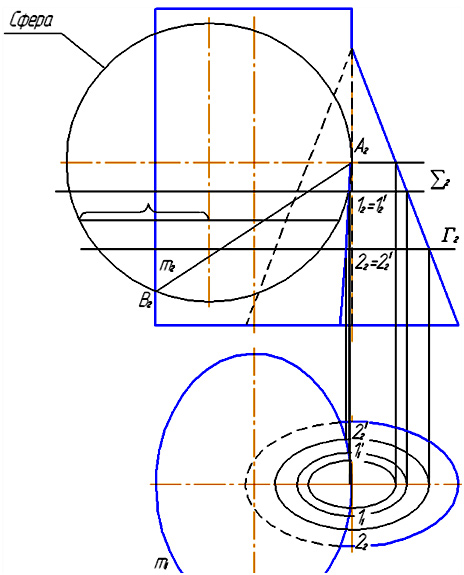
Пересечение окружности m с поверхностью эллиптического конуса
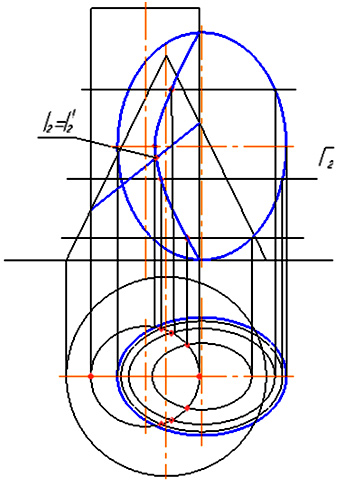
Построение точек пересечения эллипса с трехосным эллипсоидом
|
Принцев Николай Владимирович (28 февраля 2015 г. 2:14) |
Уважаемые коллеги, Ирина Алексеевна и соавторы!
Прочитал Ваш доклад, посмотрел чертежи. Согласитесь, что за такой чертёж трудно было бы получить выше тройки в школе! Линии ползут и дрожат. Изучал станок ФРГ – токарный копир. Он превосходен тем, что один авторский образец задаётся в режиме абсолютного дублирования, но здесь-то качество хуже, чем ручного чертежа. В статье говорится, что при ручном построении много трудоёмких манипуляций, а точности – нет. Так и этот чертёж можно считать весьма условным ро соблюдению размеров. А если будет увеличен масштаб? Возможность сопряжения будет уменьшаться. Студенты, глядя на такие чертежи, привыкнут к небрежности. Часто изучаю наскальные рисунки, которым несколько тысяч лет. Резьба наносилась каменным приспособлением, а «дрожания» руки мастера заметно не было. |

Головнин Алексей Алексеевич (1 марта 2015 г. 16:49) |
Здравствуйте уважаемые Ирина Алексеевна, Борис Матвеевич, Матвей Максимович, Тамара Викторовна! Возможно, я опережаю события, и еще будет ваш доклад с решением аналогичной задачи в 3D технологиях, но в любом случае, есть ли какие-то особые причины решать эту задачу в 2D технологиях, когда это можно сделать в 3D технологиях без применения алгоритмов начертательной геометрии, переложив всю эту довольно утомительную работу на компьютер? С уважением Головнин А.А. |

Волошинов Денис Вячеславович (2 марта 2015 г. 16:37) |
Уважаемые коллеги! Рад приветствовать Вас на конференции КГП-2015! Хочу высказать несколько мыслей, навеянных Вашим сообщением. Ваше внимание к методам решения задач, которыми традиционно занимается начертательная геометрия, вызывает у меня искреннюю симпатию. Конструктивные геометрические методы – математический аппарат, который может и должен использоваться для решения тех задач, в которых его применение естественно и эффективно, а потому и оправданно. Таких задач много. Теперь несколько критических замечаний. Огорчает, что в названии Вашего сообщения вы применили термин 2D- технологии. Это некорректно. Для решения представленных задач Вы используете 3D модель, выраженную эпюром Монжа. У Вас исходные объекты заданы в трехмерном пространстве, и результат Вы получаете в трехмерном пространстве. Вы используете две совмещенные картинные плоскости для выполнения промежуточных действий, но это не повод называть операции, проводимые с объектами в этих взаимосвязанных плоскостях, технологиями 2D. Если уж на то пошло, то тогда и то, что называют 3D моделированием, нужно понизить в достоинстве до 1D. Поясню свою мысль простым примером. Для того чтобы найти точку пересечения прямой с плоскостью в трехмерном пространстве, нужно решить несложную задачу с определителями матриц, размером три на три. Раскрывая эти определители, мы доберемся до уровня числа, что, по сути, есть 1D. Но эти этапы никого не заботят, поскольку спрятаны они от нашего взора в инструменте – системе моделирования. Важен результат. Построение линии пересечения поверхностей путем применения поверхностей-посредников пригодно для ограниченного числа пар линейчатых поверхностей и поверхностей вращения. Применение этого способа для более сложных поверхностей или поверхностей второго порядка общего вида приводит к громоздким построениям, сопровождающимся вычерчиванием множества лекальных кривых. Это значительно снижает точность построений. И здесь на помощь приходит вычислительная техника с графическим редактором КОМПАС-График. Далее рассматривается построение линии пересечения некоторых сложных поверхностей между собой и построение точек пересечения кривой линии с этими поверхностями. Да, в принципе, решать задачи, о которых Вы говорите в докладе, с помощью системы Компас можно. Но неудобно. И это обстоятельство будет той мишенью, которая всегда будет давать критикам повод вполне обоснованно спрашивать, а зачем все это надо? Используя систему Компас для решения задач (возможно даже очень сложных и интересных), Вы можете получить графическую интерпретацию модели, ее отображение, но, к сожалению, не действующую геометрическую модель. А потому получаемое решение всегда будет оставаться без серьезного практического применения. Компас, как система, не предназначен для решения задач такого рода. Поэтому и обосновать важность полученных результатов всегда будет очень сложно. Все это при том, что применяемые Вами конструктивные геометрические методы достойны того, чтобы ими заниматься и получать новые научные результаты. Я уверен, что Ваши исследования могут очень серьезно продвинуться вперед. Теоретически в них нет никакого порока или изъяна, но для того, чтобы это произошло, нужно обратиться к другим инструментам и увидеть ту информационную основу конструктивного геометрического метода, которая дает чертежам и схемам жизнь, которая заставляет их работать и служить средством реализации графических инфокоммуникаций. С уважением, |

Головнин Алексей Алексеевич (3 марта 2015 г. 1:21) |
Уважаемые коллеги. На этой конференции уже звучало предложение считать участие в ней прохождением повышения квалификации с выдачей удостоверений. Еще после КГП-2011 запомнились слова Владимира Адольфовича Токарева, что за два месяца на конференции научился многому – значительно больше, чем за краткосрочные курсы повышения квалификации. С тех пор после каждой КГП так себя и ощущаю даже без удостоверения. В дополнение к заданному ранее вопросу хочется поделиться впечатлением от понравившегося доклада. В начале 2011 года для себя сделал вывод, что пространственные геометрические задачи (в нашем трехмерном пространстве) с развитием компьютерной графики могут и должны решаться непосредственно в трехмерном пространстве. Но если они поставлены в виде комплексного чертежа, то могут решаться методами начертательной геометрии. Приведенный доклад, на мой взгляд, как раз и представляет такой пример, когда компьютер берет на себя роль помощника в реализации метода поверхностей посредников, когда для решения задачи используются сложные линии (эллипсы). Но сложные они только для человека с его циркулем и линейкой. Для компьютера эллипс не сложнее круга. Авторы показали это. Но этот пример, на мой взгляд, выглядит простым только для эллипса (в Компасе есть команда ЭЛЛИПС). В случае с другими линиями потребуется хотя бы программирование. В этом случае проще выглядит использование геометрического моделирования, для чего достаточно пересесть с Компас-График на Компас-3D. С уважением Головнин А.А. |

Харах Матвей Максимович (3 марта 2015 г. 17:45) |
Уважаемый Николай Владимирович! Вы, к сожалению, не поняли принципиальную суть доклада, который состоиит в том, что построение линии пересечения сложных поверхностей 2-ого порядка общего вида на компьютере является более точным по сравнению с ручным нахождением точек пересечения лекальных кривых для каждой плоскости-посредника. Согласен, что чертежи недостаточно качественные. Такова, к сожалению, материальная база кафедры. Хотелось бы познакомиться с Вашими работами. Профессор Харах М.М. |

Харах Матвей Максимович (3 марта 2015 г. 17:57) |
Уважаемый Алексей Алексеевич! Спасибо Вам за очень тактичный, уважительный вопрос в первом коментарии и профессиональный разбор нашей работы во втором коментарии. С удовольствием Вам отвечаю. В качестве 3-его РГР мы даем студентам задания на построение линии пересечения поверхностей способом вспогательных секущих плоскостей и сфер. При этом берутся простейшие поверхности вращения: цилиндр, конус, сфера. Мы планируем усложнить задачи на способ секущих плоскостей, заменив указанные поверхности вращения на поверхности 2-ого порядка общего вида и решать их с помощью графического редактора КОМПАС-График. Как Вы справедливо заметили, задачи будут легко решаться при нахождении точек пересечения эллипсов. Следующим этапом решения подобных задач будет применение 3D моделирования. С уважением, Харах М.М. |

Харах Матвей Максимович (3 марта 2015 г. 18:03) |
Уважаемый Денис Вячеславович! Сердечно благодарю Вас за столь подробный комментарий нашаго доклада. Согласен с Вашим замечанием относительно некорректного применения термина "2D технология". Имелось в виду ранее, что решение выполняется на плоском чертеже (эпюре Монжа). Будем думать над другими инструментами решения подобных задач. Еще раз спасибо за Ваши высокопрофессиональные замечания. С уважением, Харах М.М. - аспирант профессора Котова И.И. (1965-68 гг.) |
|
Чередниченко Ольга Павловна (6 марта 2015 г. 15:18) |
Конечно, это не наука. Статья о методике преподавания. Она полезна уже тем, что сотрудники других вузов могут познакомиться - что и как преподают на родственных кафедр. Можно и возражать, и соглашаться. Но мне понравилась отраженная в этой работе мысль, что двумерные построения, в отличие от трехмерных, хороши тем, что задачу самостоятельно решает студент, а не программа. И компьютер - это всего лишь инструмент, ускоряющий процесс работы. |