

|
Хорев Игорь Владимирович | (ООО "ProЭксперт") |
В статье рассмотрены концептуальные основы фрактальной геометрии как составной части науки о хаосе, приведены описания технологий использования в инженерной графике. Дан краткий обзор областей применения в различных отраслях науки и техники.
Наука о хаосе, имеющая в своей структуре фрактальную геометрию, возникла как совокупность методов решения ряда экономических задач, методов моделирования живых и турбулентных систем, которые стали возможны после появления достаточно мощных компьютеров и другого оборудования, необходимого для математического и функционального анализа нашего мировоззрения.
Теория Хаоса - это первый подход, успешно моделирующий сложные формы (живые и неживые) и турбулентные потоки, в соответствии со строгими канонами математичес-кой методологии.
Фрактальная геометрия, один из инструментов теории хаоса, используется для изучения феноменов, которые являются хаотическими только с точки зрения евклидовой геометрии и линейной математики.
Фрактальная геометрия изучает закономерности, проявляемые в структуре природных объектов, процессов и явлений, обладающих явно выраженной фрагментарностью, изломанностью и искривленностью. Они создают новую геометрию, в которой пространство не цельноразмерное, а дробное, или фрактальное.
Достаточно большое число объектов на поверхности Земли и атмосфере подчиняются степенным законам. Моделированию этих закономерностей и занимается фрактальная геометрия.
Цельноразмерная Евклидова геометрия – это 39 аксиом (по Давиду Гильберту). Новую фрактальную геометрию мы будем описывать дополнительно еще двумя аксиомами – аксиомами многомасштабности и самоподобия.
Фрактальный анализ произвел революцию в характере исследований, ведущихся в несметном количестве различных областей науки: метеорологии, медицине, геологии, экономике, метафизике.
Фрактал(лат. fractus — дроблёный) – сложная геометрическая фигура, обладающая свойством самоподобия, т.е. из всей фигуры можно выделить части, подобные целой фигуре. Примеры самоподобных множеств известны с XIX века. Термин «фрактал» (от лат. fractus – раздробленный) впервые ввел в 1975 году математик исследовательского центра IBM Бенуа Мандельброт.
Фракталы можно разделить на несколько видов:
Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.
Бенуа Мандельброт (один из выдающихся первооткрывателей Хаоса) совершил кардинальный прорыв, который можно кратко представить в виде простой математической формулы:
z -> z2 +c ;
Стрелка (->) означает итерацию - процесс реагирования, в котором конечный результат последнего расчета становится начальной константой следующего выражения:
Z2 + c превращается в "z" в ходе следующего повторения.
Это не статическое уравнение. Подобно самой жизни, это динамическое уравнение, существующее во времени. Когда итерация становится квадратичным процессом, результаты предсказуемы и быстро достигают бесконечности:
1.1 х 1.1 = 1.21х1.21 = .461 х1.461 =2.14358, и т. д.
Тоже будет верно и для любого не комплексного числа, которое меньше единицы.
Оно быстро становиться бесконечно малым:
0.9 х 0.9= 0.81 х 0.81 = 0.06561 х0.6561 = .43046 и т. д.
Однако, прибавляя константу " с " (комплексное число ) к квадратичному процессу и полагая первоначально "z" равное нулю, можно получить стабильные итерации, которые не будут приводить ни к бесконечно большим, ни к бесконечно малым числам. Эти числа будут находиться в пределах черной зоны набора Мандельброта. (См. рис.1)
Подобно погоде, фондовый и товарный рынки, а также и другие хаотичные системы, могут порождать непредсказуемые последствия при пренебрежимо малых изменениях в количествах (как в случае с данными о безработице ), помноженных на реакцию на них. Это отражает поведение в четвертом измерении, реальном мире, где Хаос очевиден и является основной структурой большинства упорядоченных систем. Набор Мандельброта, определяющийся формулой, названной в честь ее изобретателя, невозможно было бы создать без использования компьютеров и компьютерной графики. Эта формула является динамическим выражением, основанным на итерации (расчеты базируются на постоянном реагировании) комплексных чисел, началом которых является ноль.
Результат этой формулы можно наблюдать при помощью компьютерных расчетов и графического представления этих чисел. Формула кратко суммирует множество результатов Мандельброта, полученных благодаря фрактальной геометрии природы - мира, или благодаря четвертому измерению. Полученная картина совершенно отличается от идеального мира евклидовых форм: первого, второго и третьего измерения.
Рассмотрим применение фрактальный алгоритм для моделирования живых систем.
Рекурсивное построение фрактала листа папоротника:
Для построения используется процедура (псевдокод):
procedure fern(p0,h,ψ,side,δ,rec){
if (rec=0) or (k2*h< δ) then exit;
p1=p0+[0,k1*h]*R(ψ)
p2=p0+[0,k2*h]*R(ψ)
line(p0,p2) /* процедура построения отрезка по двум точкам */
fern(p1,m1*h,ψ-side*(φ1+φ0),-side,δ,rec-1)
fern(p2,m2*h,ψ+side*(φ2+φ0),side,δ,rec-1)
fern(p2,m3*h,ψ-side*(φ3-φ0),side,δ,rec-1)
}
R(ϕ) = cos(ϕ) sin(ϕ) – матрица поворота на угол φ.
- sin(ϕ) cos(ϕ)
Параметры процедуры:
Рекомендуемые значения углов и коэффициентов:
ϕ0=14,9∘,ϕ1=37,7∘,ϕ2=36,8∘,ϕ3=17,6∘,k1=0,0483,k2=0,162,m1=0,371,m2=0,336,m3=0,849.
Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1,φ2,φ3. (См. рис. 2 - верхнее изображение).
Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале (−10∘;10∘) можно получить изображения: (см. изображения 3,4 рис.2 ).
Рассмотрим другое применение фрактальной геометрии – для анализа графиков колебаний цен на биржах.
Следует отметить, основные положения теории хаоса были сформулированы именно на основе анализа поведения цен на рынках. Колебания курсов валют являются одним из наиболее востребованных сфер применения фрактального анализа.
В настоящее время не существует чёткого математического определения фрактала. Применительно к биржевой торговле фрактал определяется как замкнутый промежуток, на котором размещается изменение цены. Фрактал составляется из пяти последовательных баров или свеч. Фрактал всегда означает изменение в поведении; он отражается как последовательность из пяти баров, где центральный бар (или группа) имеет более высокий максимум для фракталов на верх и более низкий минимум фракталов вниз.
На рис. 5 представлен график курса валютой пары евро - доллар США с обозначенными фракталами.
На рис. 6 рассматриваются основные виды торговых фракталов.
Один из способов торговли с помощью фрактала состоит в следующем: если рынок преодолевает внешний экстремальный максимум для фрактала наверх или минимум для фрактала вниз, двигайтесь в сторону внешней направленности фрактальной точки.
Кроме того, фракталы позволяют силу толчка цены вверх или вниз. Безусловно, фрактальный анализ не является единственным и достаточным инструментом для успешной торговли, но является ключевым для адекватного понимания сущности рынков.
Сфера применения фрактальной геометрии будет расширятся по мере роста мощности компьютерного оборудования для её визуализации.
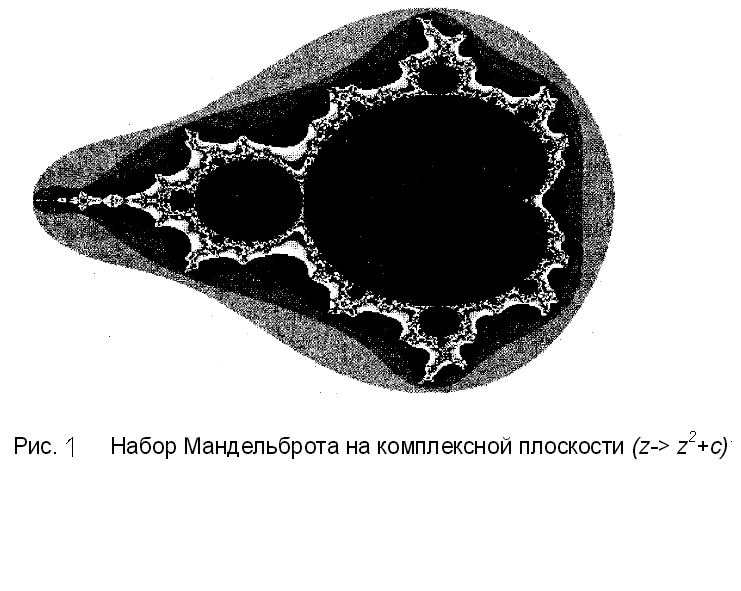
Набор Мандельброта на комплексной плоскости
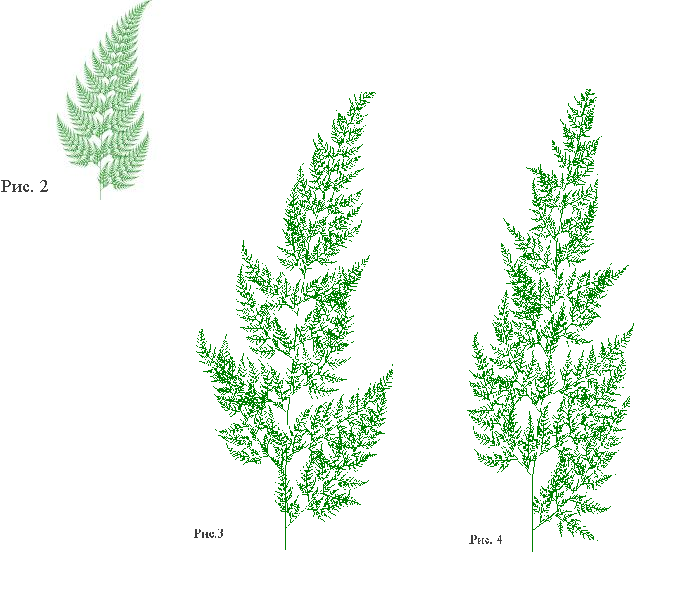
Фракталы папоротника
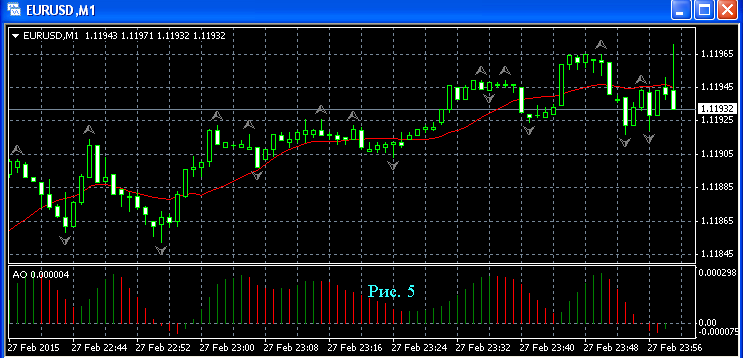
График курса валютой пары евро - доллар США с обозначенными фракталами
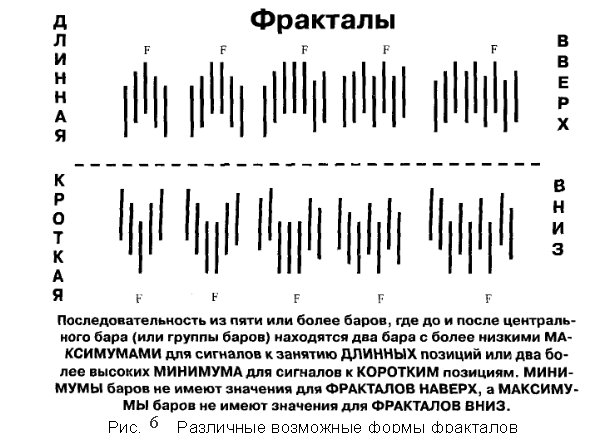
Основные виды торговых фракталов

Шахова Алевтина Бруновна (3 марта 2015 г. 21:17) |
Здравствуйте Игорь Владимирович, мы коллеги Марии Гавриловны, в конференции есть рубрика "Портреты" и в память о замечательном грамотном преподавателе черчения и геометрии Хоревой Марии Гавриловны можно было было бы дать описание ее биографии, что наверное в полной мере можете воспроизвести только Вы. Доклад очень интересный и познавательный для всех геометров. Спасибо. С уважением Шахова А.Б. |

Мокрецова Людмила Олеговна (4 марта 2015 г. 1:58) |
Добрый вечер, Игорь Владимирович! Давно ждала начала дискуссии по поводу достижений в области фрактальной геометрии. Большое спасибо за доклад, думаю , что ее место не только в в "инфографике", но и в и моделировании любых пространственных форм. Нам надо серьезно заниматься фрактальной геометрией и разрабатывать методики ее преподавания. С уважением, Л.О.Мокрецова |

Дударь Елена Сергеевна (10 марта 2015 г. 13:10) |
Игорь Владимирович, спасибо за интересный доклад! Для желающих подробнее познакомиться с основами фрактальной геометрии автор любезно предоставил в оргкомитет электронные версии книг: В.К. Балханов «Основы фрактальной геометрии и фрактального исчисления» и монографию Билла Вильямса «Новые измерения в биржевой торговле…». С позволения автора привожу его отзывы о книгах, в которых в доступной форме изложен «очень сложный материал. Это просто музыкальность в области мысли и логики. Это действительно талантливо и заслуживает внимания». Елена С. Дударь |