

|
Горнов Александр Олегович | (Национальный исследовательский университет "МЭИ") |
Рассмотрено обобщение одного приема построения натурального вида плоских фигур, в том числе общего положения, по их проекциям.
Речь пойдет об обобщении элементарной задачи и приема её решения в рамках традиционных методов начертательной геометрии. Представляется, что со всех точек зрения становится всё более актуальным поиск обобщений, возможностей сжатия и уточнения положений и методов НГ как средств, полезных на стадии целеполагания (синтеза эскизных изображений и соотношений), мониторинга и анализа комплекса 2D изображений в рамках задач ИГ, решаемых как средствами традиционных, так и компьюторных технологий.
С этих позиций вашему вниманию предлагается маленький пример такого обобщения одного из элементарных приемов анализа натуральной конфигурации точек на плоскости (вершин плоской фигуры), занимающей, в том числе, общее положение. Подчеркиваю, что цель не в том, чтобы сравнить другие приемы с данным. Главное – рассмотреть эту процедуру как обобщающую для любых положений плоскости фигуры и полезность обобщений вообще.
Как известно, построение дополнительного вида на плоскую грань в проецирующем положении или фигуры в плоскости такого же наклонного сечения является простой процедурой построения её характерных точек по координатам дополнительной прямоугольной системы координат (ОСК, UCS), лежащей в плоскости фигуры. При этом, одна координата без искажения считывается на одной проекции 2D системы изображений, а вторая на другой. Это считывание координат с разных проекций можно легко обобщить для построения фигур, лежащих в плоскостях общего положения. Такую возможность обеспечивают ведь две из главных прямых плоскости, а именно: фронталь и горизонталь (для пары H и F традиционных плоскостей проекций), исходящие из одной точки – начала образуемых ими косоугольной системы координат. При этом истинная величина каждой координаты точки в этой системе равна её ортогональной проекции на соответствующую ось такой координатной системы.
Далее надо обратиться к иллюстрации на рис. 1. Для простоты чертежа указанные выше построения для определения таких координат выполнены для одной точки (А) фигуры. Определение натуральной величины угла β̀ между осями этой системы координат (f,h) на рисунке видно из простых построений. Ясно, что указанный угол β̀ для проецирующих положений плоскости фигур равен 90º, т.е. косоугольные координаты становятся ортогональными. Проще или сложнее использовать косоугольные координаты в каждом конкретном случае, - это другой вопрос. Важнее возможность единого подхода, показать еще одну полезную нагрузку линий частного положения и проекции прямого угла.
Этот прием, конечно, обратим. Можно задать положение точки в плоскости таких косоугольных координат при натуральном значении β̀ и построить её соответствующие ортогональные проекции. Коллеги без труда смогут определить две проекции точки B, заданной на том же рисунке в плоскости h∩f .
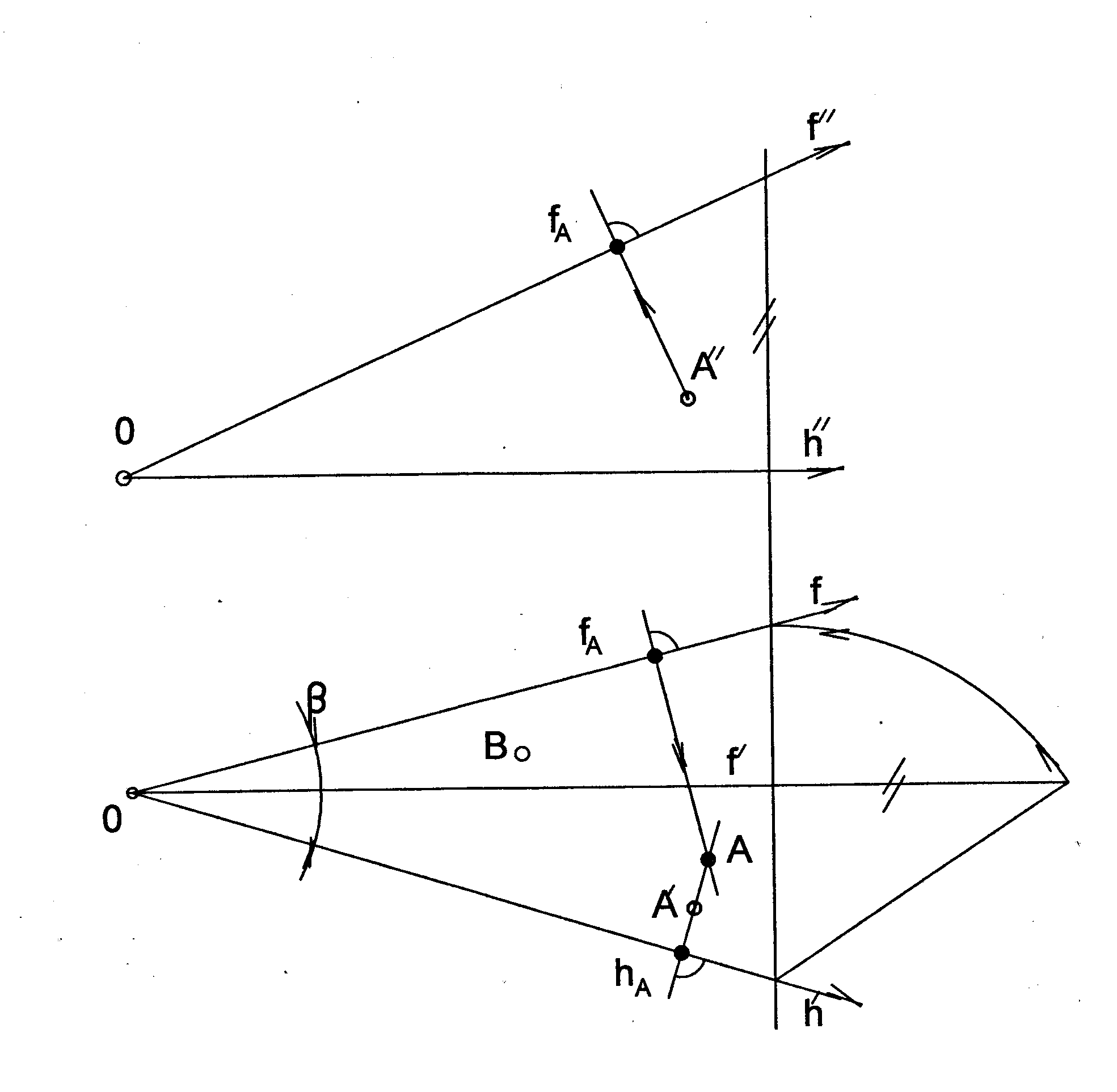
Определение координат точки в косоугольной системе
|
Принцев Николай Владимирович (7 марта 2015 г. 1:55) |
Уважаемый Александр Олегович! Спасибо за Ваш подготовленный доклад по рассмотрению практических вопросов. Наверное, такие задачи следовало бы преподавать в наших Автошколах, где сегодня, увы, из водителей пытаются готовить в прямом смысле санитаров. Много времени отводится проблемам оказанию первой помощи. А ведь если будет решение проекционных задач, что на трассе должно решаться "на автопилоте", то и аварийность снизится. |

Мокрецова Людмила Олеговна (8 марта 2015 г. 0:48) |
Николай Владимирович! Вряд ли надо ориентироваться на Автошколы, ведь ряд ученых России, в том числе и в нашем вузе, работают над созданием беспилотного автомобиля. Тут есть где развернуться. С уважением, Л.О.Мокрецова
|