

|
Волошинов Денис Вячеславович | (Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А.Бонч-Бруевича) |
В статье ставятся вопросы создания инструментальной программной среды для проведения геометрического эксперимента. Внимание читателей обращается на то, что основная задача геометрии состоит в установлении соответствий между геометрическими объектами. Обращается внимание на роль мысленных и натурных геометрических экспериментов, предназначение которых заключается в информационной поддержке научной, познавательной и практической деятельности человека, связанной с решением геометрически обусловленных задач. Сформулированы основные требования, которым должен удовлетворять программный инструмент, предназначенный для проведения геометрического эксперимента.
Геометрия как научная дисциплина всегда отличалась от иных наук двумя основными качествами – наглядностью и строгостью. Сказанное, конечно же, ни в коей мере не направлено на принижение роли и значимости тех отраслей знания, которые отличны от геометрического. Но, так или иначе, геометрия всегда ассоциировалась и ассоциируется поныне с теми методами ведения рассуждений, которые основываются на истинах-постулатах, четкой предрасположенностью к строгим логическим рассуждениям и выводам, подкрепляемым визуально-графическими средствами убеждения и доказательства.
Геометрические знания являются неотъемлемой частью сокровищницы человеческого опыта. На протяжении веков эта наука не только приносила чисто практическую пользу, позволяя человеку ориентироваться в мире форм и приспосабливать тем самым окружающую действительность под свои нужды, но и стала однажды тем инструментом, который позволил раздвинуть горизонты познания, понять необходимость и неизбежность различных взглядов на сущность бытия, осознать тщетность попыток поиска единственности, фундаментальности и первопричинности истины.
Геометрия родилась из опыта – эмпирики и эксперимента. Закрепившись в постулатах Евклида, развитая трудами многих замечательных мыслителей древности, геометрия в течение двух тысячелетий превратилась в свод знаний: кодекс, положения и выводы из которого многократно и успешно подтверждались практикой – критерием истины, не допускавший и мысли о своем несовершенстве [1]. Иными словами, геометрия, казалось бы, перестала нуждаться в практическом эксперименте для своего обоснования, поскольку была способна успешно предсказывать практический результат на основе лишь самой себя.
Незыблемость фундамента геометрии Евклида поколебал молодой венгерский ученый Янош Больяи [2]. Виною этого события стали мысленные эксперименты с не вполне ясными, как казалось в те времена, положениями о параллельных линиях. Пытаясь доказать постулат Евклида о параллельных «от противного», Больяи поставил однажды мысленный эксперимент и предположил, что параллельные линии пересекаются в точке (что показалось бы его современникам сущим бредом). В результате ученый пришел к парадоксальным выводам, которые привели его в смятение, лишив чувства уверенности в твердости того математического фундамента, на котором строилась современная ему геометрия. Логическая стройность рассуждений, которым следовал ученый, с одной стороны, и отсутствие эмпирических подтверждений получаемым выводам, с другой стороны, приводили его в недоумение, восторгали и пугали одновременно. Открытие Больяи не было, да, видимо, и не могло быть понято современниками. Величайший математик того времени Карл Гаусс, который, видимо, подошел в своих исследованиях достаточно близко к идеям Больяи, все же не решился поддержать его взгляды. Все эти обстоятельства, в конце концов, привели к прогрессированию душевной болезни и трагической кончине молодого ученого.
Идеи Больяи нашли свое практическое подтверждение позже. Они раздвинули границы нашего познания в области и физических, и математических наук, позволили понять, что стройность логических рассуждений – неотъемлемый атрибут геометрической науки и следование логике в геометрии не подвергается никакому сомнению. Зато логика эта может быть применена к различным базисам. И это обстоятельство сближает геометрическую науку и с философией, и с информатикой, бурно развивающейся в наши дни. Современное понимание практической и научной ценности геометрии проистекает из информационной сущности явления моделирования, которое раскрыл в ней однажды Янош Больяи. И в этом смысле геометрический метод является ценным инструментом, сочетающим в себе логику и наглядность, возможность ставить и проводить над геометрической моделью абстрактный или же практический эксперимент.
Необходимо, конечно же, сказать, что идеи геометрического моделирования не являются идеями абсолютно новыми. Геометрия и до Больяи была средством моделирования, ибо позволяла заменять своим аппаратом реальность, использовать его для предвидения. Другое дело, что долгое время она не осознавалась таковой и лишь только в двадцатом веке обрела должное понимание, подкрепленное положениями и обоснованиями теории информации.
Наделенная вышеперечисленными достоинствами, геометрия обладала одним существенным ограничением. В определенной мере она страдала скудостью того инструментария, который мог быть использован для сопровождения мыслительного процесса и для практических воплощений полученных ее теорией результатов. Эти инструменты хорошо известны: карандаш, циркуль и линейка. Безусловно, существуют и несколько более сложные и, если так допустимо выразиться, «изощренные» инструменты для продуцирования геометрических чертежей и схем, но все же приходится признать, что перечень этот не столь широк, а более или менее сложные механические устройства и автоматы непросты в эксплуатации и требуют от применяющего их человека наличия специальных знаний. Некоторые (даже хорошо изученные) геометрические операции исключительно трудоемки. Прямых инструментов для их воплощения не существует, и поэтому большинство из них требуют последовательного скрупулезного и многократного применения циркуля и линейки. В этой связи, конечно же, нельзя не упомянуть относительно низкую точность выполнения чертежно-графических работ ручными инструментами. А в деле использования мнимых образов, образов отрицательных размерностей [3], без которых геометрия, попросту говоря, неполна, и в наши дни есть еще столь много белых пятен в понимании сути дела, что говорить о более или менее значимой инструментальной поддержке геометрических операций с их участием почти не приходится. В связи с этим нельзя не отметить тот неоценимый вклад, который вносит своими научными исследованиями А.Г.Гирш [4] в деле воссоздания полноты геометрии за счет соединения ее действительного аппарата с мнимыми образами, предложениями по их визуализации и использованию в практических задачах.
Все эти обстоятельства, которые уже неоднократно обсуждались в геометрическом сообществе, являются тормозом развития геометрической науки. Геометрии нужен инструмент, который способен работать со свойственными ей понятиями и объектами и в необходимом для этого ключе. Только тогда она может стать практически действенным инструментом моделирования, в результате чего можно будет ставить не только мысленный, но и реальный эксперимент. И только тогда геометрия перестанет ассоциироваться с феноменом черчения, связь с которым, безусловно, ценна, но не всеобъемлюща. Разумеется, в современных условиях таким инструментом может стать программная система, построенная в соответствии с обозначенными выше принципами.
Разговор об особенностях и принципах построения инструмента такого рода хотелось бы продолжить, ибо у автора есть многолетний опыт создания подобной программного продукта. И он, вероятно, был бы полезен тем, кто хотел бы решать геометрические задачи, не приспосабливая к ним доступные, но не вполне пригодные для этого инструменты. Возможно, этот опыт был бы полезен и тем коллегам, кто чувствует в себе силы разработать нечто подобное или даже значительно более совершенное программное средство, предназначенное для решения задач в истинно геометрической постановке. Это дело вполне реальное и, более того, было бы в высшей мере полезно для геометрии. Однако в рамках одной ограниченной в объеме статьи изложить данный вопрос системно и в исчерпывающей полноте, конечно же, невозможно. Здесь, видимо, необходим цикл статей, тематика которых будет вынужденно выходить за рамки сугубо геометрических проблем, ибо создание такой системы – это комплекс теснейшим образом взаимосвязанных задач, имеющих отношение собственно к геометрическому моделированию, логике, системному анализу, программированию, эргономике интерфейса, теории управления и многими другим областям знания.
Никоим образом не преследуя соображения какой-либо исключительности или навязывания своего видения, автор хотел бы поделиться имеющимся у него опытом и некоторыми соображениями по этому вопросу. Именно поэтому данную статью хотелось бы рассматривать как постановочную, вводную, и сконцентрировать в ней внимание лишь на некоторых отправных задачах, связанных с проведением геометрического эксперимента. Эти задачи, возможно, покажутся слишком простыми в своей постановке, а может быть и странными. Но, видимо, только так можно показать принципиальную разницу в подходах к созданию и использованию средств автоматизации. Следует четко обозначать причины появления тех трудностей, которые возникают при попытках приспособления для решения геометрических задач систем автоматизации конструкторских работ. Предлагаемые вниманию читателя задачи построены на исключительно простых логических рассуждениях, но, несмотря на эту простоту, они призваны обратить внимание не только на философские основы геометрического метода, но и на глубинные вопросы бытия вообще. Эти эксперименты – мыслительные или натурные – несложно реализовать в заинтересованной студенческой группе. Подобные эксперименты за считанные минуты ломают годами сложившиеся стереотипы, позволяют учащимся осознать, что картины окружающего мира могут быть разными и внешне весьма непохожими друг на друга, разобраться в том, как это различие понимать и рационально использовать в своих целях.
Обсуждение хотелось бы начать со слов К.А.Андреева, опубликованных в [5].
«Во всех исследованиях древних геометров данные, а следовательно и искомые, при всяком построении рассматриваются в неизменном состоянии, и это составляет отличительный характер древней Геометрии пред Геометрией новой. В последней напротив изменяемость положения данных и искомых, а с тем вместе и понятие о соответствии, установленным тем или другим родом построения, играет преобладающую роль и составляет характеристическую особенность всех основных принципов и методов.
Все новейшие способы исследования состоят почти исключительно в преобразовании одних фигур или геометрических форм, свойства которых нам известны, в другие, свойства которых подлежат изучению, преобразовании, которое, в сущности, есть не что иное как установление геометрического соответствия.
Итак, повторяем, идея о соответствии есть основная во всей новой Геометрии» [5].
Хочется подчеркнуть, что мысль К.А.Андреева, концентрированно выраженная в последнем процитированном абзаце, исключительно современна. Это та путеводная нить, которой следовало бы придерживаться в любых приложениях геометрического метода, – в практических применениях, в образовании, в создании средств автоматизации. В ней как нельзя лучше отражена подлинная гносеологическая сущность геометрии, то, что должно определять ее развитие на многие годы вперед.
Итак, ссылаясь на слова К.А.Андреева, еще раз отметим, что геометрический метод заключается прежде всего в установлении соответствий между фигурами или иными геометрическими формами.
Как правило, понимание природы соответствий, ее элементарных первооснов дается студентам, начинающими изучать геометрический метод, не так легко. Надо честно сказать, что некоторые, казалось бы, элементарные вопросы могут поставить и преподавателя, занимающегося геометрией профессионально, в определенное затруднение. Виною тому сложившиеся стереотипы, которые прочно ассоциируют в нашем сознании абстрактные геометрические образы с реальными физическими объектами, закрепляют за ними те качества, которых в них реально нет. Так, например, на простой вопрос – состоит ли прямая линия из точек – большинство респондентов с уверенностью ответят, что да, состоит, хотя это совсем не так.
Внимательный читатель, разумеется, разглядит в этом вопросе некоторый подвох. Действительно, что означает слово «состоит»? Казалось бы, оно требует разъяснений, определений и т.п. Однако ни одно из определений, которые мы попытались бы дать, суть дела не прояснит. Цепочка уточнений уведет нас в бесконечный цикл определений и «уточнений», требующих своих «уточнений», и не даст в конечном счете никакой ясности [6].
Поэтому освободимся от соблазна что-либо уточнять. Не будем требовать определений, а следуя исключительно соображениям здравого смысла (инвариантной неопределенности), зададим себе эквивалентный вопрос: как провести через две несовпадающие точки прямую линию, если образца (экземпляра) линии у нас нет. То есть две точки присутствуют, но нет линейки, с помощью которой линию можно было бы провести.
Простой, казалось бы, в постановке вопрос, оказывается неразрешимым, ставит собеседника в затруднение. Никакими «ухищрениями» не удается провести «прямую» линию через две точки, не опираясь на презумпцию понятия прямой. Получается, что природа точки и прямой разная, это классы различных объектных множеств, и «построить» одно из другого, не опираясь каким-либо образом друг на друга, оказывается невозможным. Поэтому следует заключить, что прямая линия не состоит из точек. Но из этого последует и еще более «странный» вывод о том, например, что две несовпадающие прямые никогда не могут пересекаться в точке, поскольку объекты множества одной природы не могут иметь ничего общего с объектами природы принципиально другой.
Мысленный эксперимент приходит в противоречие с повседневным утилитарным опытом, над сознанием довлеют стереотипы. Между тем никаких ошибок и парадоксов в сказанном на самом деле нет. Действительно, обратившись к аксиомам Евклида, обнаружим, что прямая – это объект, который единственным образом можно провести через два несовпадающих объекта другого рода, называемых точками. Но нигде не указано, как это сделать (и какого вида эти объекты). То же самое можно сказать и относительно пересекающихся прямых. Две несовпадающие прямые пересекаются (на плоскости) в точке, но нигде не сказано, каким образом эту точку определить. Аксиомы накладывают некоторые ограничения, но они и оставляют место для свободы. Вероятно, их действие можно попытаться применить и к объектам, имеющим «начертание» отличное, от того, к которому привыкло наше воображение, и при этом логического ущерба от такого приложения может и не быть?
Мысленные неувязки и ошибки, с которыми мы сталкиваемся в рассуждениях о соотнесении хотя бы только точек и прямых друг с другом, кроются в некорректном отношении к процессам моделирования, недопонимании этого явления. Абстрактное понятие «точка», который мыслится как объект, не имеющий ни длины, ни высоты, ни ширины, заменяется нами предметно частичкой графита на бумаге, мела на доске, песчинками на берегу моря, пикселом на экране монитора, наконец. Замена эта правомерна в принципе, но незримо, за геометрией на уровне подсознания в модель проникает физика, которой в исходном моделируемом объекте (абстрактной точке) нет. Точке начинают приписываться те качества, которые ей не присущи. Эта малозаметный, но серьезный недочет, который, выражаясь словами К.А.Андреева, является одной из причин недопонимания отличия геометрии новой от геометрии древней.
И все же, как же быть с формулировкой постулата, утверждающего, что две прямые линии пересекаются в точке? Ответ на самом деле достаточно прост и расставляет все точки над i. Прямая линия не состоит из точек, но может их на себе нести. Хотелось бы обратить внимание на то, что в указанном контексте «состоять» и «нести на себе» – понятия различные. Прямая линия может нести на себе т.н. линейный ряд точек, размещать их на себе. Представленный в виде предметной модели в виде частичек графита на бумаге линейный точечный ряд визуально неотличим от изображения прямой. Однако это визуальное совпадение, вносящее большую путаницу, скрывает в себе принципиально разные природы наблюдаемых феноменов. Визуально неотличимые линейные точечные ряды, расположенные на одной прямой, могут быть различными и различие это можно указать лишь через определение соответствий между объектами этих рядов, тогда как их прямая-носитель единственна. Но, сколь бы различными ни были эти ряды, два линейных точечных ряда будут иметь на двух несовпадающих линейных носителях единственную общую точку, и именно об этой точке идет речь, когда говорят о том, что две прямые линии, расположенные в плоскости, пересекаются в точке.
Справедливости ради нужно отметить, что рассуждения, проводимые в традиционной постановке, не помешали человечеству построить города, запустить электростанции, вывести на космические орбиты рукотворные аппараты. И ими разумно пользоваться, если такое применение не мешает решению поставленной задачи. Но на определенных этапах жаргон (а это действительно научный жаргон) не позволяет увидеть сущность явления с иных, не вполне привычных позиций. А это одна из причин торможения развития геометрической науки.
Рассуждения, о которых только что шла речь, не являются для геометрии чем-то принципиально новым. Так, например, в теории проективной геометрии хорошо изучены преобразования, устанавливающие взаимно-однозначное соответствие между точками и прямыми. Таковыми, например, являются полярное соответствие, коррелятивное преобразование. Взаимная однозначность, индуцируемая проективными соответствиями, позволяет текстуально заменять в теоремах проективной геометрии понятия «точка» и «прямая» друг на друга, что, однако, не приводит к появлению каких-либо противоречащих друг другу утверждений. Подобная замена известна под названием принципа двойственности; эффект, достигаемый такой формальной процедурой, трудно переоценить.
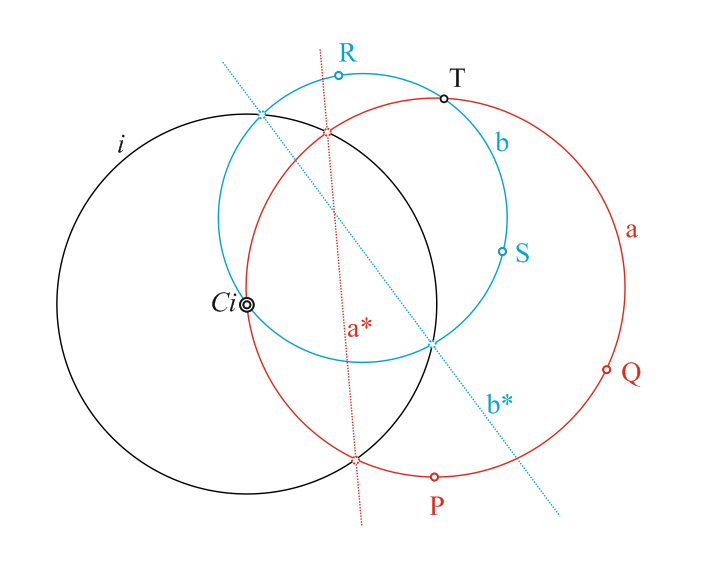
Но вернемся к точкам и прямым. Нетрудно показать, что аксиоматика евклидовой геометрии может быть с успехом применена и к другой геометрической системе. Предположим, что имеется обычная плоскость. Плоскость несет в себе поле точек, которые, так же, как и обычные точки, заполняют ее. Выделим среди всех точек всего одну Ci, за которой закрепим особое свойство (рис. 1). Эта точка будет характеризоваться той особенностью, что она станет общей для всех «прямых» линий, расположенных в названной плоскости, т.е. будет инцидентна с ними всеми.
Нетрудно догадаться, что единственным образом через две различные точки P и Q плоскости плюс одну фиксированную особую точку Ci можно провести окружность a. Поскольку две исходные точки можно выбрать произвольным образом, а последняя точка для всех таких окружностей одна и та же, то такую точку можно исключить из рассмотрения. Тогда получается, что через две различные точки плоскости единственным образом проходит объект, который в соответствии с аксиоматикой Евклида допустимо называть «прямой» линией. Окружность проходит через три точки, каждая из которых имеет две степени свободы – итого шесть. Но, поскольку каждая из точек может, перемещаясь по той же окружности с одной степенью свободы, определять ту же окружность, то общее параметрическое число снижается до трех. Поэтому множество всех окружностей на плоскости трехмерно. Но за счет того, что одна из точек фиксирована, она отнимает еще одну степень свободы, и, следовательно, размерность множества окружностей, проходящих через фиксированную точку, снижается до двух. Поэтому предложенная замена прямой линии окружностью правомерна. Разумеется, этот объект, окружность-«прямая», при обычном ручном построении выглядит и воспринимается человеком, как окружность, но его проявления и геометрические свойства подчинены аксиоматике Евклида, относящимся к «обычным» точкам и прямых. И в этом смысле окружность становится логически неотличимой от прямой линии. Построим, для примера, другую «прямую» b и пересечем ее с «прямой» a. В результате получим единственную точку Т, как и должно было бы быть.
Несложно увидеть, что предложенная схема является эквивалентом преобразования обратных радиусов или инверсией относительно окружности i с центром инверсии в фиксированной точке Ci. Соответствие между образами и прообразами в этом преобразовании инволюционно: окружности и прямые линии переходят друг в друга (a–a*, b–b*). И логический, и натурный геометрический эксперимент с объектами в этом преобразовании, в особенности, если он выполнен с применением компьютерных технологий, позволяет быстро изучить и запомнить свойства, проявляемые в соответствиях между объектами. Эксперимент дает возможность на основе применения даже такой исключительно простой геометрической схемы еще раз убедиться в том, что суть геометрического познания заключается в «преобразовании одних фигур или геометрических форм, свойства которых нам известны, в другие, свойства которых подлежат изучению» [5].
Похожую идею можно распространить и на другие геометрические объекты. Возьмем, как и в предыдущем примере, плоскость, на которой выберем теперь не одну, а три неколинейные точки. Зафиксируем их. Добавим к ним еще две точки таким образом, чтобы любая тройка точек из имеющихся пяти точек не лежала бы на одной прямой, и проведем через полученные пять точек конику, которая единственным образом ими определяется. Коника проходит через пять точек, каждая из которых имеет две степени свободы – итого десять. Но, поскольку каждая из точек может, перемещаясь по той же конике с одной степенью свободы, определять ту же конику, то общее параметрическое число снижается до пяти. Поэтому множество всех коник на плоскости пятимерно. Но за счет того, что три точки выбраны фиксированными, они отнимают от общего числа параметров еще три степени свободы, и, следовательно, размерность множества коник, проходящих через три фиксированные точки, снижается до двух. Поэтому предложенная замена прямой линии коникой правомерна. В соответствии с намеченным в предыдущем примере планом, мы можем назвать конику прямой линией, поскольку свойства, проявляемые такими кониками-«прямыми» будут соответствовать аксиоматике Евклида. Нетрудно заметить, что всевозможные пары коник, проходящие через три фиксированные и любые пары свободных точек будут иметь в пересечении только одну точку. Действительно, поскольку две коники-«прямые» пересекаются в четырех точках (действительных или мнимых), при наличии трех фиксированных общих точек свободной остается только одна точка, которую и следует считать точкой пересечения таких «прямых».
Приведенная геометрическая схема так же, как и в предыдущем случае, может быть представлена геометрическим преобразованием, в котором устанавливается соответствие между объектами плоскости. Этим преобразованием является инволюционное квадратичное преобразование плоскости Q, которое переводит точки плоскости в точки, а прямые линии в коники. Для разъяснения сути обсуждаемых проблем опишем схему этого преобразования лишь вкратце.
Пусть на плоскости заданы две несовпадающие коники a и b. Выберем на этой плоскости некоторую точку M и найдем образы этой точки в поляритетах pa и pb, индуцируемых кониками a и b. Этими образами являются две прямые – поляры ma и mb. В свою очередь, поляры ma и mb, пересекаясь, определяют новую точку M* – образ исходной точки в квадратичном преобразовании, заданном двумя кониками a и b.
Несложно показать, что данное преобразование в целом инволюционно. Найдем две поляры для полюса M* относительно двух исходных коник a и b. Это будут две прямые линии na и nb, которые в пересечении определят геометрическое место точки M.
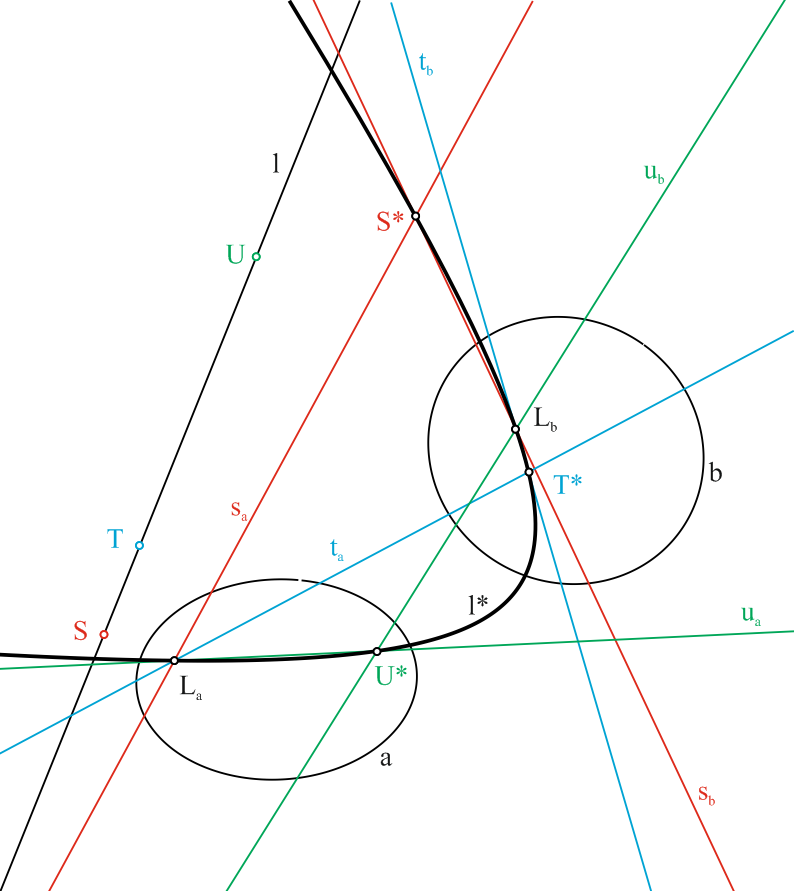
Пусть теперь в плоскости дана некоторая прямая линия l (рис. 2). Определим, какой геометрический образ будет соответствовать прямой линии в квадратичной инволюции. Выберем на прямой три несовпадающие точки S, T и U и преобразуем их в поляритетах pa и pb. В результате получим два соответственных пучка прямых La(sa,t a,ua) и Lb(sb,tb,ub). Центры этих пучков La и Lb и точки пересечения соответственных лучей S*=(sa sb), T*=(ta tb) и U*=(ua ub) определят пять точек, через которые пройдет единственная коника l* – результат преобразования прямой линии в квадратичной инволюции.
Предположим, что на плоскости задан пучок прямых с центром в точке A. Преобразуем этот пучок в квадратичной инволюции. Тем самым мы получим пучок коник, каждая из которых пройдет через образ точки A – A*. Любые две коники пересекаются в четырех точках, следовательно, если принять во внимание, что точка A* уже определена, то должно остаться еще три точки B*, C*, D*, для которых определено и обратное преобразование в силу его инволюционных свойств. Однако, если взять любую из трех оставшихся точек, скажем B*, и найти ее прообраз B, то это означало бы, что две исходные прямые – прообразы коник должны были бы пересекаться помимо точки A еще в точке B, что противоречит предположению о различии исходных прямых. Следовательно, оставшиеся три точки пересечения коник должны подчиняться каким-то иным правилам и их, вероятно, следует соотнести с особыми свойствами преобразования квадратичной инволюции.
Зададимся целью исследовать эти три точки и определить, являются ли они единственными в преобразовании квадратичной инволюции, или же они не единственны и составляют некоторый геометрический образ.
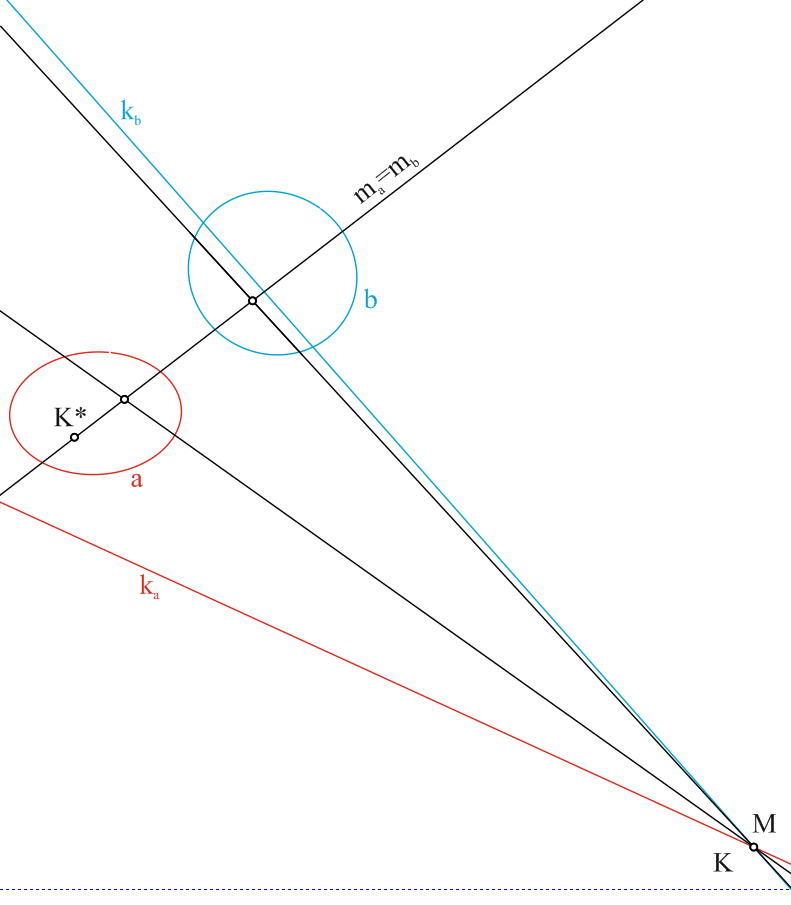
Рассмотрим преобразование более подробно и попытаемся разобраться, действительно ли каждой точке плоскости в квадратичном преобразовании соответствует точка, или же в нем существуют какие-либо исключения (рис. 3). Понятно, что поскольку точка M в поляритетах pa и pb относительно каждой из исходных коник a и b преобразуется в поляры ma и mb, то вероятной является ситуация, что поляры ma и mb совпадут. Казалось бы, что такие две поляры можно считать параллельными и в своем пересечении они дадут единственную бесконечно удаленную точку M*. Однако это не совсем так.
Возьмем на поляре ma произвольную точку К*. Преобразованная в поляритете pa эта точка образует поляру ka. Теперь соотнесем точку К* c полярой mb и эту точку в поляритете pb . В результате образуется поляра kb. Разумеется, и ka, и kb должны проходить через точку K=M, поскольку ma и mb совпадают. В силу произвольности выбора точки К* на ma=mb следует заключить, что точке K в квадратичной инволюции соответствует не единственная и, тем более, не бесконечно удаленная точка К*, а прямая линия ma=mb. Поэтому рассматривать прямые ma=mb как параллельные и находить точку их пересечения недопустимо!
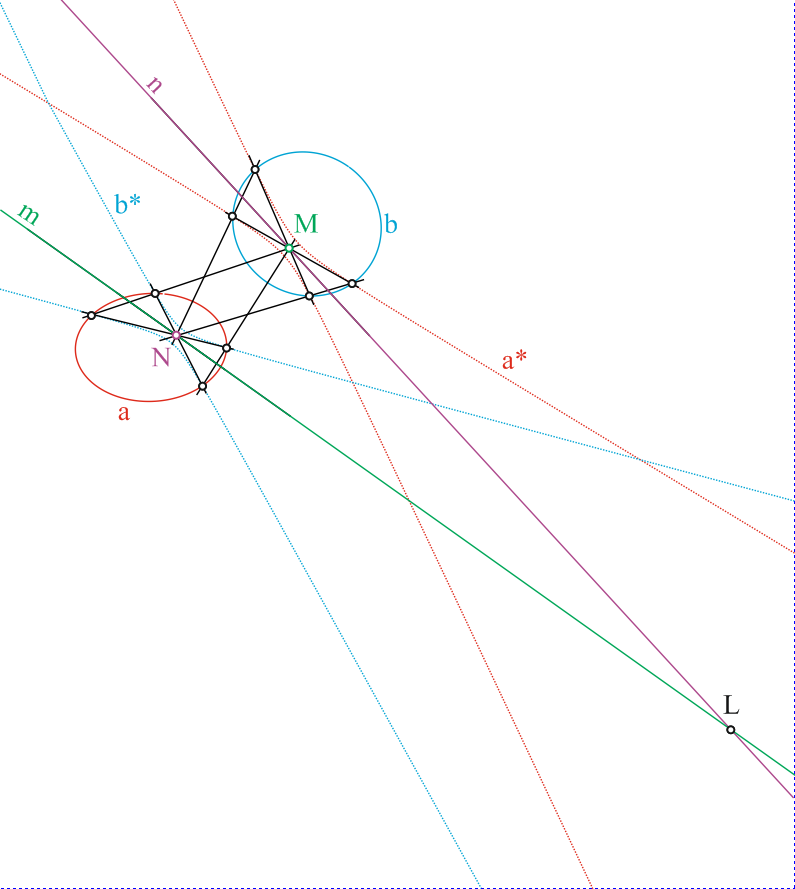
Если совпадение поляр ma и mb обнаруживается, то это означает, что точка M одинаково переводится обеими кониками a и b в одну прямую. Предположим, что положение полюса M известно (рис. 4). Выберем конику a и преобразуем вторую конику b относительно нее вместе с прямой-полярой m=ma=mb. Получим конику-прообраз b* коники b в поляритете pa=–pa, при этом поляра m отобразится в полюс M. Найдя четыре точки пересечения коники a с b* , построим на них полный четырехугольник. Одна из оставшихся вершин укажет нам положение полюса M. Вторая вершина определит положение полюса N – точки, которой также соответствует прямая линия в квадратичной инволюции Q, если бы мы рассмотрели преобразование в поляритете pb=–pb коники a относительно b. Определив положение точек M и N, которым в квадратичном преобразовании соответствуют прямые линии, а не точки, проведем через них прямую линию mn. Эта прямая, преобразованная в поляритетах pa или pb, образует еще одну точку L. Таким образом, имея три точки M, N и L, мы можем построить три прямые линии mn, ml и nl, которым в квадратичной инволюции соответствуют не коники, а точки M, N и L. Любой из точек, взятой на одной из этих прямых, будет соответствовать одна и та же точка на плоскости. Поэтому, взяв любую прямую, не совпадающую с mn, ml и nl, мы будем обнаружим точки ее пересечения с этими прямыми, а в преобразовании мы получим конику-образ, проходящую через три точки M, N и L. Фиксированность геометрического места этих точек, определяемая двумя исходными кониками преобразования Q, является фундаментальным организующим свойством преобразования квадратичной инволюции и все коники – образы прямых проходят через три фундаментальные точки.
Сравнив рассмотренную только что геометрическую схему с предложением называть прямыми линиями коники, проходящие через три фиксированные и две свободные точки, мы обнаруживаем в них общую геометрическую природу.
Анализ геометрических схем, которые были приведены выше, и эксперимент с геометрическими моделями позволяют наглядно показать интересные особенности, на которые зачастую не обращают внимания. В частности, очень интересным и поучительным оказывается анализ исключенных элементов модели и исключительных ситуаций. Выполняя мощную организующую роль, исключения присутствуют в каждой модели, и в то же время эти явления еще недостаточно подробно изучены даже для простых геометрических построений. Возьмем, для примера, декартову плоскость, дополненную бесконечно удаленной прямой. Это расширение весьма удобно для логических рассуждений, поскольку оно позволяет избавиться от случаев, когда из точки плоскости нужно провести прямую линию в точку пересечения прямых, которые по каким-либо причинам стали параллельными. Фактически это означает, что взяв произвольную точку плоскости, мы должны провести линию в бесконечно удаленную точку, что есть то же самое, что провести линию, параллельную двум заданным прямым. Однако надо понимать, что этот прием возможен только в случае выбора собственной точки плоскости. Ежели провести прямую в бесконечно удаленную точку из несобственной точки плоскости, то такая прямая совпадет с бесконечно удаленной прямой. Казалось бы, действуя по предписанному правилу, эту прямую следовало бы также назвать прямой, параллельной заданной, но делать этого нельзя, поскольку в таком случае несобственная прямая стала бы параллельной любой прямой плоскости, что означало бы параллельность вообще любых прямой плоскости. Поэтому, избавившись от одного вида исключений, мы непременно приобретаем другие, что и показывает данный пример. Это важный философский вывод!
Если обратиться к примеру инверсии, то и в нем можно обнаружить интересные исключения. Так, например, инверсия, индуцированная окружностью, переводит бесконечно удаленную прямую в точку – центр инверсии. Таким образом, бесконечность стягивается в единственную точку, которая является собственной точкой плоскости. А вот несобственных элементов в этом преобразовании попросту нет.
Весьма интересен в этом контексте и последний пример. Если под кониками понимать прямые, то недопустимо считать, что эти «прямые» пересекают друг друга в фундаментальных точках. Визуальный опыт и логика здесь расходятся, и предпочтение следует отдать логике, а не глазам. Между прочим, бесконечно удаленная прямая в этом преобразовании, как и прочие прямые, переходит в конику. Такая коника является одной из коник пучка параллельных коник-«прямых», однако она тоже является исключительной и выпадает из понятия параллельности, поскольку является общей для любого пучка коник, моделирующих параллельные прямые разных направлений.
Приведенные нами примеры исключительно просты в своей постановке. По сути дела мы рассмотрели операцию проведения прямой линии через две точки, но представленную в различных геометрических базисах. Несмотря на кажущуюся простоту формулировок задач, мы обнаружили, что их решение требует достаточно мощного геометрического аппарата, а для проведения эксперимента с объектами этих задач нужен специализированный инструмент.
Наступает время подводить итоги. Но перед тем, как это сделать, необходимо, видимо, ответить на возникающие у читателей вопросы: зачем нужно «усложнение» простого; какую практическую пользу могут принести рассмотренные выше замены понятий; соотносится ли то, о чем было изложено выше, с тем, к чему все мы привыкли и чем пользуемся повседневно; стоит ли всем этим заниматься?
Отвечать на такие вопросы всегда трудно. Трудно не потому, что на них нельзя дать убедительного ответа, а потому, что в ограниченных объемах статьи невозможно осветить широту проблемы в исчерпывающей полноте. Примеры и рассуждения, которые были приведены здесь, – это мизерная ее часть.
Геометрия – это математическое средство моделирования, область ее приложений неисчерпаема. Ценность модели состоит в ее работоспособности, в ее адекватности, в пригодности для осуществления замен одних сущностей сущностями другими. Информационный ущерб для лиц, проводящих эти замены, должен быть равен нулю или же сведен к минимуму. Изучение моделей сложных в контексте установления соответствий с моделями более простого вида направлено на возможность увидеть в сложном знакомое, понятное и относительно простое. В частности, пример, в котором было кратко рассмотрено преобразование квадратичной инволюции, – это маленький шаг на пути к теории кремоновых преобразований [7, 8], и в нем было показано, что межу простыми прямыми линиями и линиями второго порядка можно обнаружить интересную и полезную взаимосвязь.
С методами использования кремоновых преобразований в области проектирования авиационной техники можно познакомиться на примере исследований Г.С.Иванова [9]. Даже беглый просмотр этой книги убедит читателя в том, что это мощный аппарат и он не прост для понимания. Но, конечно же, дело не только в этих преобразованиях. Еще раз хочется сказать, что геометрия неисчерпаема.
Приходится признать, что даже в настоящее время у нас нет подлинно геометрического инструмента, который позволил бы применять подобный геометрический аппарат в практической проектной деятельности. И часто единственным способом применить к чему-либо сложную геометрию остается перевод ее метода в аналитическую форму. Поэтому задача создания и развития такого инструмента, который позволил бы ликвидировать эту «брешь», дал бы возможность упростить работу с геометрическим аппаратом, экспериментировать с ним, познавать его, видится задачей исключительно важной. В противном случае методы наподобие кремоновых преобразований будут либо невостребованными, либо окажутся доступными лишь немногим посвященным.
Каким бы хотелось видеть этот инструмент?
Первое, и, наверное, самое важное требование: он должен соответствовать духу геометрии. То есть давать возможность исследователю, учащемуся или проектировщику работать с информацией, представленной в геометро-графической форме и постановке.
Второе: этот инструмент должен предназначаться для создания, отладки и эксплуатации работающих моделей или, иными словами, специализированных компьютерных программ. Именно это качество К.А.Андреев определяет за геометрией как главное, и инструмент должен соответствовать этому требованию.
Третье: инструмент должен допускать гибкую замену и формирование понятий, их синтез и анализ. Необходимость этого обусловлена общей методологией научного познания.
Четвертое: инструмент должен поддерживать работу с несобственными объектами, реализовывать все основные преобразования евклидовой (как частной) и проективной геометрии. Это качество позволяет решать геометрические задачи в многомерной постановке. Объекты и операции должны быть определены как для действительных, так и для мнимых геометрических образов.
Эти четыре требования автор считает необходимым выделить, как главные: они определяют область проводимых исследований. Конечно, есть и другие требования, но они имеют более частный характер. Их освещение – дело отдельного разговора.
Преобразование инверсии
Преобразование прямой линии в конику в квадратичной инволюции
Исключенные элементы квадратичной инволюции
Построение фундаментальных точек квадратичной инволюции
|
Принцев Николай Владимирович (10 марта 2015 г. 11:19) |
Прекрасный доклад! Сочетание древности, современности и прогноза на будущее. Главное, аргументированный, убедительный стиль. |

Головнин Алексей Алексеевич (10 марта 2015 г. 22:50) |
Здравствуйте уважаемый Денис Вячеславович! 1. В процессе использования компьютерной графики прочувствовал нечто похожее с Вашим примером о точке и прямой. Мы привыкли, что две прямые на плоскости пересекаются в точке, впрочем, как и любые другие линии на плоскости. Но попытки привязаться к месту пересечения при помощи привязки ТОЧКА показывают, что точки там нет, пока мы принудительно не поместим туда точку командой ТОЧКА при помощи привязки ПЕРЕСЕЧЕНИЕ (пересечение есть, а точки нет). У человека имеет место эвристическое мышление, у компьютера же пока – только логическое, и логике, строгости мышления, у него можно поучиться. 2. Ранее уважаемый Сергей Игоревич Ротков напомнил нам, что специальность 05.01.01 – инженерная геометрия и компьютерная графика в номенклатуре специальностей ВАК относится к техническим наукам. В вашем докладе трудно усмотреть непосредственную связь с техникой. Естественно, это не минус, но для меня, например, как механика (техническая наука) в любой геометрии хочется увидеть понятное приложение к технике. Возможно, я не прав в своих представлениях о начертательной геометрии только как о грамматике языка техники, но знакомство с работами без практического уклона, считаю очень полезным для себя. С уважением Головнин А.А. |

Волошинов Денис Вячеславович (11 марта 2015 г. 8:39) |
Здравствуйте, Николай Владимирович! Большое спасибо за высокие слова о докладе! |

Волошинов Денис Вячеславович (11 марта 2015 г. 9:53) |
Здравствуйте, Алексей Алексеевич! Благодарю Вас за внимание к моему сообщению! Хотел бы дать некоторые пояснения и ответы на Ваши комментарии.
|