Авторы изучили наследие французского учёного Жозефа Луи Лагранжа, считая, что его отдельные математические положения ещё в недостаточной степени нашли применение в прикладных науках. Преподавание Начертательной геометрии сегодня находится в прямой зависимости от правильной интерпретации исторических основ, известных сегодня под Школой Лагранжа.
Ключевые слова: Начертательная геометрия, Нобелевская премия, Школа Лагранжа, Жан Жак Руссо, Леонид Канторович, Жан Тироль,
Научная Новизна
Авторы впервые предприняли попытку ознакомить научную геометрическую общественность с исследованиями учёного по лингволаконике Георгия Фёдоровича Ершова, который связывает воедино научный опыт Лагранжа и Жан Жака Руссо, а также влияние работ по Начертательной геометрии Лауреата Нобелевской премии – Леонида Витальевича Канторовича на лауреата Нобелевской премии 2014 года – Жана Тироля. Сокращение образовательных программ по Начертательной геометрии в РФ связано с тем, что Жан Тироль стал сотрудничать с Парижским Университетом Дофин, который был создан в бывшей Штаб квартире НАТО в Париже. Авторы впервые делают акцент на том, что курс Начертательной геометрии является стратегическим в системе образования РФ [1]. Поэтому, повышая уровень преподавания Начертательной геометрии, в РФ обеспечивается константа национальной образовательной независимости.
Цель данного исследования – рассмотреть значение Начертательной геометрии в новом расширительном толковании её значения.
Введение
Современная математическая наука в лице академика В.Арнольда высказывает сожаление о том, что студенты, увлекаясь интегральным вычислением и компьютеризацией образовательных процессов, проявляют полную беспомощность не только при решении каких-либо практических задач, но и пасуют перед выполнением самых элементарных арифметических действий. В ракурсе исправления качества самих экзаменационных испытаний В.Арнольд предлагает ввести правило исключительно письменного экзамена по математике. Авторы, изучив сложившуюся ситуацию, пришли к выводу, что проблема кроется в другой плоскости. На наш взгляд, чрезмерный «академизм» современного отечественного и зарубежного образования не позволяет в полной мере раскрыть талант тех учёных, которые в своей ежедневной практике опирались на совершенствование экспериментальной доказательной базы. Таким учёным как раз являлся Лагранж, наследие которого не изучено подробно до настоящего времени, тогда как рассмотрение данной темы в рамках её ретроспективного влияния на развитие отдельных разделов науки представляется авторам весьма своевременным.
Начертательная геометрия и снайперское мастерство экономических расчётов
Объём данной статьи не позволяет в полном объёме проанализировать влияние Научной Школы Лагранжа на дальнейшее развитие различных отраслей науки, включая экономические науки. Историки, занимаясь узкими темами, не сопоставляли взаимовлияние Жан Жака Руссо и Лагранжа. Как это нередко бывает, Лагранж, будучи моложе Руссо почти на двадцать лет, но сумев занять в 19 лет должность профессора в Артиллерийской Академии города Турина, заставил Руссо переосмыслить некоторые экономические трактаты. Юный Лагранж не мог не увлекаться геометрией, наделяя её новым экономическим содержанием. Именно ему принадлежит выражение:
- Каждый выстрел – попадание в цель.
Приводим пример интерпретации теоремы Лагранжа (рис.1), которую использовал Канторович в своей «фанерной» тематике [2].
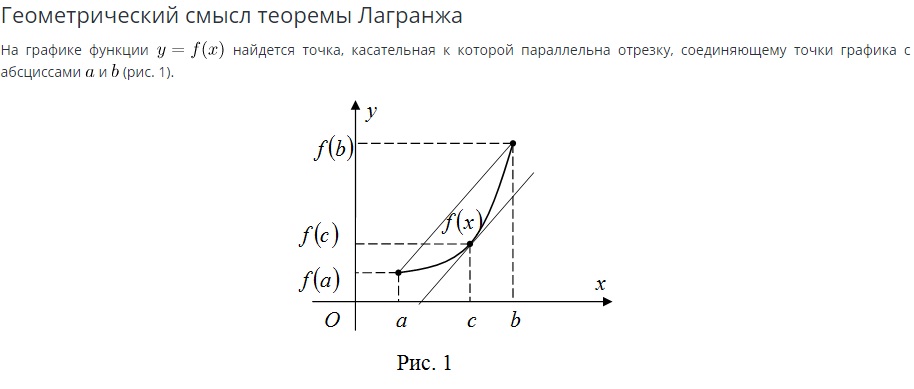
Конечно, о научных взаимоотношениях Лагранжа и Руссо, а также об эмигрантах из России, проживавших во Франции и в Италии в 18 веке, авторы познакомились из работ известного лингволаконика – Георгия Фёдоровича Ершова, но сейчас мы считаем необходимым остановиться на следующих малоизвестных фактах. Г.Ф. Ершов, в совершенстве владея мастерством технического перевода, столкнулся с тем, что работы Леонида Витальевича Канторовича, выпущенные в нашей стране в 1935 году, когда он получил степень доктора наук без защиты диссертации, тут же переводились на французский, немецкий, английский языки и даже на американский диалект (американские технические тексты, не говоря уже о литературных, отличаются от английского языка, как русский язык от украинского).
Изучая многочисленные зарубежные архивы, встречаясь с учёными, Ершов Г.Ф. пришёл к выводу, что была предпринята «охота» за исследованиями Канторовича, особенно за его приложением, разработанным на основе наследия Лагранжа.
Сегодня многие саркастически упоминают о том, что СССР имел фанерные самолёты в годы Великой Отечественной войны, тогда как авиационная фанера имела целый ряд преимуществ, которые не утратили своей актуальности и сегодня. Канторович, имея свои исторические корни в Белоруссии, использовал одновременно чисто «крестьянский» подход в учёте каждой мелочи в производственном процессе с расчётом артиллерийской точности, предлагаемой ранее Лагранжем.
Открытия учёного Г.Ф. Ершова
Обладая талантом исследователя, Г.Ф. Ершов смог в результате многолетней работы за рубежом и поездок по России доказать, что интерес Лагранжа к военным наукам появился отнюдь не на пустом месте. Формально, Лагранж получил «домашнее» образование. Но, каким образом, имея отца-чиновника, далёкого от солидных математических знаний, юный Жозеф овладел не только фундаментальными математическими знаниями, но и способностью решать массу практических задач по Начертательной геометрии? Ответ был найден Ершовым при изучении семейных архивов эмигрантов из России, которые были вынуждены покинуть страну по разным причинам, озвучивание которых может составлять тему отдельного исследования. Не останавливаясь в данной статье на истории выходцев из тех или иных регионов Российской Империи, которые стали учителями Лагранжа, будем констатировать, что было заключено некое негласное соглашение, которое Жан Жак Руссо в своих сочинениях обозначил, как «Условия Общественного Договора». В данном случае «Лагранж» в тот период считалось названием научного сообщества, которое могло в легальных рамках продвигать научные идеи, не опасаясь политических репрессий и финансовых санкций.
Леонид Канторович, поступив в 1926 году в Ленинградский университет в возрасте 14 лет, уже к 22 годам имел степень доктора наук, продолжив опыт Лагранжа. То есть здесь был использован принцип Франшизы, но наоборот. «Обратная функция Франшизы», как шутливо говорил Канторович, уже будучи в зрелом возрасте. Не надо забывать, что время признания заслуг Канторовича приходится на 1935 год, когда бушевало Ленинградское дело в связи с убийством Сергея Мироновича Кирова в декабре 1934 года. И как в своё время юный, безусловно талантливый, Лагранж стал надёжным плащом, под которым могла прятаться от тайной канцелярии научная интеллигенция того периода времени, так и имя молодого Леонида Канторовича стало надёжным щитом для развития блистательных, смелых технологических решений для учёных Города на Неве. Повторяем, объём данной статьи не позволяет более подробно осветить эти увлекательные периоды развития математической мысли и творческого развития Начертательной геометрии.
Туринский и Тулузский синдромы Начертательной геометрии на современном этапе
Сегодняшняя Нобелевская премия в области экономики за 2014 год является перепевом мотивов Лагранжа с изрядным заимствованием положений из работ Канторовича. Жан Тироль, закончив Политехническую школу, основанную ещё Гаспаром Монжем, решил сделать акцент своих научных исследований на применении в экономике методов Начертательной геометрии. Он попытался сделать себе имя в математике, занимаясь исследованиями работ Лагранжа, преподававшего в Политехнической школе в конце своей жизни. Однако за рубежом, Школа геометров в последние десятилетия не радует серьёзными исследованиями, поэтому Тироль решил пойти по пути копирования нашего опыта. Попеременно Тироль пытался произвести неумелую компиляцию из трудов академика Прохорова и Канторовича, не углубляясь в постановку научных проблем. Тем не менее, герб Политехнической школы – два скрещённых ствола пушек шёл ещё от традиций Лагранжа, преподававшего в Артиллерийской академии. Поэтому-то и саму Политехническую школу называли Школа – Х (икс) и также называли её выпускников «Х», намекая на их некоторую загадочность. Что мы можем констатировать на современном этапе? «Условия Общественного договора», о котором столь таинственно поведал в своих работах Жан Жак Руссо, значительно изменились в 21 веке. Если раньше зарубежная наука, в первую очередь Начертательная геометрия, подпитывалась идеями и большим ассортиментом интересных практических задач, то Нобелевская работа Жана Тироля грешит откровенным мелкотемьем. Так, если мы сегодня возьмём рабочие журналы, которые вёл Леонид Витальевич Канторович, занимаясь модернизацией производства авиационной фанеры, то это можно будет применить на любом производстве, получив обнадёживающие результаты. Авторы не ставят в данной работе поставить цель в точности установить, какая мысль преобразований принадлежала непосредственно молодому Канторовичу, а что было предложено более опытными товарищами. Нам важен полученный результат.
Исходя из символики цифр, можно заключить, что в 22 года Канторович получил научную степень доктора наук, а Жан Тироль в 22 года узнал о том, что Канторович получил Нобелевскую премию по экономике, задавшись целью достичь таких же результатов. Узнав, что Канторович творил в Северной Столице, где мосты являются не только техническими сооружениями, но и архитектурными шедеврами, он поступил в магистратуру при Национальной Школе мостов и дорог в Париже [4]. Однако путь его в «большую» науку лежал через «большую» политику. Когда Франция решила выйти из НАТО, то в бывшем здании Штаб квартиры НАТО, возник Международный университет – Дофин [5], который и выдал диплом доктора наук по математике Тиролю, страстно мечтавшему о Нобелевской премии. Но для этого надо было провести определённое число лет в качестве «преподавателя» в США, где получает он статус «экономиста», а в 1992 году он возвращается во Францию и активно занимается «социальными преобразованиями». Насколько известно сегодняшним отечественным преподавателям Начертательной геометрии, эти «преобразования» в немалой степени коснулись и их дисциплин.
Заключение
Начертательная геометрия стала объектом пристального изучения зарубежных «преобразователей» именно потому, что образно-графическое наследие Лагранжа, дополненное исследованиями Канторовича, поднимали уровень отечественного образования на недосягаемую высоту, что и доказывалось значительным научным прорывом отечественных учёных в различных отраслях знаний. Толерантность современного школьного образования с отказом от преподавания астрономии, черчения, труда, а также сокращение программ по начертательной геометрии в вузах преследует цели зарубежных «советчиков». Эти цели означают не только снижение общего образовательного уровня, но и смены ментальности, как таковой в РФ.
Выводы:
- Расширительное изучение работ Лагранжа в курсе Начертательной геометрии может значительно повысить коэффициент экспериментальности студентов [3], то есть заставит их решать и самим разрабатывать новые практические задачи, потому что курс Лагранжа изначально в Турине был основан как конгломерат практических задач по Начертательной геометрии.
- Современное комплексное изучение параметров Лагранжа неопровержимо приведёт к теоретическим и практическим работам Леонида Витальевича Канторовича, которые заключают в себе значительный научный потенциал.
- Освоение опыта (решение практических задач Начертательной геометрии) Лагранжа сможет решить целый ряд вопросов, в том числе в области экономики, что будет рассмотрено авторами в отдельной статье.
Список литературы
- Б.М. Яворский, А.А. Детлав // Физика для инженеров // Издательство «Наука», Главная редакция физико-математической литературы / Москва 1971г. 939с.
- В.С. Щипачёв // Высшая математика // Издательство «Высшая школа» / Москва 2007 г. 408с.
- А.А. Чекмарёв // Начертательная геометрия и черчение // Издательство «Владос» / Москва 2002г. 470 с.
- А.Э. Гутнов, В.Л. Глазычев // Мир архитектуры // Издательство «Молодая гвардия» / Москва 1990г. 350с.
- С. Альтман // Анализ орбитальных движений методом годографов // перевод с англ. Издательство «Мир» / Москва 1968 г. 151с.
Рисунки к докладу
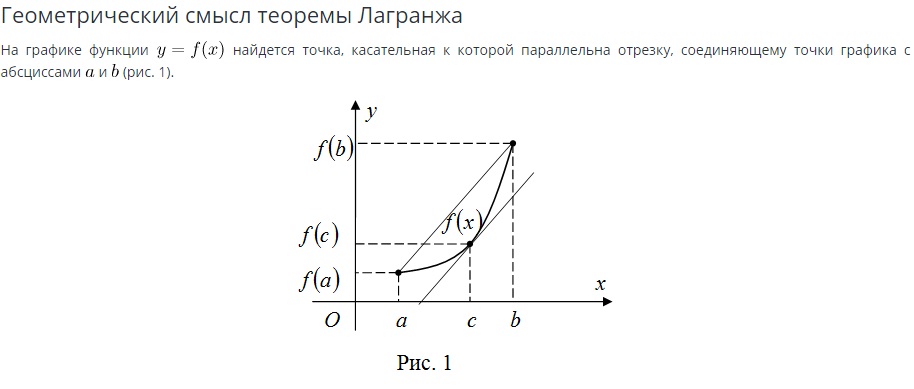
Рис. 1
Вопросы и комментарии к выступлению:
|
Принцев Николай Владимирович (11 марта 2015 г. 11:36) |
Уважаемые Коллеги! Жду Ваших комментариев, потому что Начертательная геометрия становится объектом борьбы политиков в мире! Только об этом мало, кто задумывается! С уважением ко всем, Н.В. Принцев. |

Сальков Николай Андреевич (11 марта 2015 г. 13:03) |
Здравствуйте, Николай Владимирович! То, что НГ является стратегической наукой, понимал ее основоположник Монж (он писал об этом в своей Программе), знаете Вы, и понимают многие из геометров, хотя некоторые на фоне просто несущейся галопом компьютерной графики вдруг решили, что НГ устарела - есть у нас такие партнеры. И теперь вместо усиления роли НГ мы видим ее ликвидацию по многим направлениям обучения. Вы копаете значительно глубже, выявляя забугорных кукловодов, хотя среди нас по этому поводу такие мысли высказывались. Лагранж был соратником Монжа, профессором в созданной Монжем Нормальной школе, а затем возглавлял кафедру математики в знаменитой Политехнической школе, опять же, созданной Монжем, откуда и вышли все великие французские ученые-геометры. Отсюда и его интерес к НГ, поскольку Монж подавляющее большинство занятий отдавал именно изучению математики, куда он приписывал и НГ. Н-да, надо изучать первоисточники! С уважением, Сальков.
|
Назад Go Back