МЕТОДИЧЕСКИЕ ТРАДИЦИИ И ТЕНДЕНЦИИ ПРЕПОДАВАНИЯ МАТЕМАТИКИ С ИСПОЛЬЗОВАНИЕМ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Представлено обобщение традиций и опыта преподавания математики в среде современных информационных технологий. Предлагается организация обучения в виде активной лекции - модели аудиторной лекции, которая может использоваться как при чтении обычной лекции, так и при индивидуальном изучении, а также виртуальный лабораторный практикум, основанный на ознакомлении с примерами и выполнении разнообразных упражнений с использованием информационных технологий.

ВВЕДЕНИЕ

В условиях сохраняющейся тенденции к сокращению аудиторного времени, выделяемого учебными программами на изучение курса высшей математики, информационные технологии открывают новые возможности для модернизации содержания обучения и методов преподавания.

Производительность в контексте использования компьютера означает автоматизацию нетворческих, рутинных операций, отнимающих у обучающегося много сил и времени. Достигаемая при этом экономия учебного времени позволяет существенно расширить ряд рассматриваемых в курсе математики примеров и задач, иллюстрирующих внутренние и внешние связи различных разделов курса друг с другом, с иными дисциплинами, а также будущей профессией.

Утверждение информационных технологий как инструментального средства и средства совершенствования содержания учебных дисциплин открыло для них аналогичные возможности, но поставило ряд  аналогичных задач.  

У   визуальной - “графической” геометрии - в дидактическом аспекте и в приложениях - есть несколько, образно говоря, пересечений с аналитическими моделями математики, которые проецируются и на задачи совершенствования преподавания графических дисциплин и математики. Тут и проблемы межпредметных связей и совершенствования структур основных образовательных программ  [1].

Мультимедийные обучающие системы позволяют гармонично объединить лекцию с демонстрацией учебного материала, практикум в виде компьютерного имитатора, тестирующую систему и все дополнительные материалы в едином интерактивном компьютерном учебнике.

В докладе представлен  «Программно-методический комплекс по изучению элементов высшей математики», обеспечивающий повышение эффективности математического образования студентов, в том числе  нематематических специальностей.

Комплекс предназначен для компьютерной поддержки разделов общеобразовательного курса «Высшая математика». Доступны варианты представления математических понятий для разных специальностей с иллюстрацией  применения изучаемого понятия  соответственно специальности.

Положительный опыт использования компьютерных обучающих программ в математике базируется на следующих предпосылках: накоплен огромный опыт в формализации и алгоритмизации методов решения задач, их графической и анимационной интерпретации; применяются апробированные, хорошо реализуемые с помощью компьютера, дидактические приемы и методики преподавания.

При разработке программного комплекса по математике учитывались следующие основные психолого-педагогические теории усвоения знаний [2].

Применение теории программированного обучения в линейной и разветвленной форме является стержневым фрагментом программного комплекса по численным методам, что предусматривает: правильный отбор и разбиение учебного материала на небольшие порции, частый контроль знаний, переход к следующей порции лишь после ознакомления учащегося с правильным ответом или характером допущенной им ошибки, обеспечение возможности каждому обучаемому работать со свойственной ему, индивидуальной, скоростью усвоения.

Исходя из теории поэтапного формирования умственных действий и понятий представляется целесообразным создание у обучаемых необходимой познавательной мотивации, а также разработка схем ориентировочных основ действий, позволяющая им успешно овладевать каким-либо действием. Предоставление студенту реальных задач из его профессиональной области является эффективным средством  мотивации обучаемых.

Основу ассоциативно-рефлекторной теории составляет раскрытие содержания и последовательности деятельности обучающихся, это реализовано в программном комплексе с помощью единого педагогического сценария обучения. Также установление ассоциаций - условно-рефлекторных связей с помощью напоминаний учебного материала  как из изучаемого раздела, так и из других разделов математики.

Проблемное обучение реализовано в строго продуманной системе проблемных ситуаций, проблем и задач, соответствующих познавательным возможностям обучаемых. Теория проблемного обучения при разработке программного комплекса использовалась при создании обстановки интеллектуального затруднения в тестовых упражнениях с запланированными ошибками.

1. МОДЕЛИ КОМПЬЮТЕРНОГО ПРЕДСТАВЛЕНИЯ УЧЕБНОГО МАТЕРИАЛА В СОВРЕМЕННОМ МАТЕМАТИЧЕСКОМ ОБРАЗОВАНИИ

Рассмотрим следующие модели компьютерного представления учебного материала в современном математическом образовании [3,4]:

1. Модель  аудиторной  лекции - организация  лекционного материала по математике  в  виде активной  лекции.

При  обучении  математике  для  доказательств  теорем  и вывода алгоритмов наиболее существенным является совместный творческий процесс  преподавателя  и   студента,   когда   лектор ставит   цель доказательства,   акцентирует   внимание   на   условиях ,   на  которых оно  основывается,  и  получает  результат  последовательно, строка  за  строкой, вместе со студентами, развивая у них активное внимание и движение  мысли за мыслью лектора,  иллюстрируя процесс соответствующими геометрическими построениями и примерами, задавая вопросы и предлагая возможные варианты ответов, комментируя ошибки и неточности ответов студентов.

На основе вышеизложенного предлагается  организация  обучения  математике  в  виде активной  лекции - модели  аудиторной  лекции, которая может использоваться как при чтении обычной лекции, так и при индивидуальном изучении. При  этом  выводы  и  доказательства подаются компьютером постепенно – построчно или абзацами. Лекционный материал включает в себя не только текстовую и графическую информацию, но также анимационные эффекты, а предоставление необходимой информации по запросу студента приближает его к обучению, проводимому под руководством преподавателя.

Используя математические апплеты (написанные на языке Java), студент получает возможность с помощью визуализации наглядно представить процесс решения, построения, вывода. Возможные варианты реализации – постепенное появление информации на экране при движении курсора, моделирующее записи лектора на доске и зависящее от выбранной студентом скорости. При этом ему также предоставляется возможность свобод­но путешествовать в предоставленной  лекции, например, вернуться  к началу доказательства или вывода, повторить непонятые участки, то есть  участвовать в процессе формирования и представления  учебного  материала.

2. Виртуальный лабораторный практикум, основанный на ознакомлении с примерами и выполнении разнообразных упражнений. Планирование сценариев каждого примера и упражнения (также построенных на основе Java-матлетов) осуществляется в соответствии с универсальной бихевиористской теорией обучения, согласно которой материал разбивается на мелкие дозы и подается поэтапно. При рассмотрении примеров после постановки задачи и задания начальных данных студенту предлагается шаг за шагом с подробными пояснениями проследить процесс нахождения ответа. При этом существует связь элементов текста не только с графической иллюстрацией, но и с помеченными данными и используемыми формулами. Применение таких технологий существенно активизирует учебную информацию, делает ее по сравнению с представлением на бумажном носителе более наглядной для восприятия и удобной для усвоения. Упражнение можно охарактеризовать, как воспроизведение усвоенных ранее знаний от буквальной копии до применения в типовых ситуациях, то есть решение задач по усвоенному ранее образцу. При выполнении упражнения осуществляются как тренирующие, так и контролирующие функции. Тренирующие функции используются для осмысления и закрепления информации, с которой учащийся знакомится, они неразрывно связаны с комментариями, являющимися информацией обратной связи. Контролирующие функции применяются при оценивании степени усвоения материала, ведется подсчет ошибок по  следующим критериям:  на знание, понимание, вычисление и применение.

Следует отметить, что при использовании предлагаемых педагогических технологий  меняется и  организация учебного процесса. При использовании активных лекций  с проектором существенно увеличивается скорость ее проведения преподавателем, поскольку  нет необходимости записывать ее и на доске и в тетради. Поэтому возможно уменьшение количества аудиторных лекционных занятий, с переносом соответствующего количества часов на самостоятельную работу студентов с конспектом активных лекций. При проведении практических и лабораторных занятий снимается необходимость решения примеров преподавателями, при этом появляется возможность проконтролировать качество выполнения упражнений  студентами по всем темам.

2. ИЛЛЮСТРАТИВНАЯ И КОГНИТИВНАЯ ФУНКЦИИ КОМПЬЮТЕРНОЙ ГРАФИКИ [5,6]

В настоящее время интерактивная компьютерная графика - это одно из наиболее бурно развивающихся направлений новых информационных технологий. Основная идея различий иллюстративной и когнитивной функций ИКГ, выделенная в работе [6] при описании использования ИКГ в научных исследованиях, хорошо вписывается в классификацию знаний и компьютерных систем учебного назначения. Иллюстративные функции ИКГ реализуются в учебных системах декларативного типа при передаче учащимся части знания, представленной в виде заранее подготовленной информации с графическими, анимационными и видеоиллюстрациями. Когнитивная же функция ИКГ проявляется в системах процедурного типа, когда учащиеся "добывают" знания с помощью исследований на математических моделях изучаемых объектов и процессов, причем, поскольку этот процесс формирования знаний опирается на интуитивный механизм мышления, сами эти знания в существенной мере носят личностный характер. Каждый человек формирует приемы подсознательной умственной деятельности по-своему.

Одним из известных эвристических подходов к развитию интуитивного профессионально-ориентированного мышления является решение задач исследовательского характера. Применение учебных компьютерных систем процедурного типа позволяет в существенной мере интенсифицировать этот процесс, сделать возможным проведение различных экспериментов на математических моделях.

 Методика и практика применения математических методов на базе ИТ постепенно смещает  акценты с использования инструментальных навыков человека (решения алгебраических, дифференциальных и  интегральных  уравнений, неравенств  и т.п.) к овладению искусством  корректного составления математических моделей на основе вышеуказанных математических соотношений и последующего  получения решений существующими программными средствами.

Именно ИКГ-изображения хода и результатов экспериментов на математических моделях позволяют каждому учащемуся сформировать свой образ изучаемого объекта или явления во всей его целостности и многообразии связей.

 При проектировании глобального сценария программно-методического комплекса целесообразным является в начале учебной работы создание у обучаемых мотивации, знакомство с общей структурой учебного материала (теории алгоритмизации или поэтапного формирования умственных действий).

При разработке локальных сценариев (последовательности выполнения упражнений в ходе изучения отдельных учебных элементов) сначала планируются к выполнению более абстрактные упражнения, а следом за ними примеры и упражнения со схемами, чертежами и другими графическими иллюстрациями (материализованная форма деятельности).

3. ПРОГРАММНО+МЕТОДИЧЕСКИЙ КОМПЛЕКС ПО ИЗУЧЕНИЮ ЭЛЕМЕНТОВ ВЫСШЕЙ МАТЕМАТИКИ

Программно–методический комплекс по изучению элементов высшей математики базируется на следующих разделах высшей математики — это «Элементы математического анализа», «Элементы линейной алгебры», «Элементы аналитической геометрии».

 Глава «Элементы математического анализа» разбита на разделы: «Введение в анализ», «Дифференциальное исчисление функции одной независимой переменной», «Дифференциальное исчисление функции нескольких независимых переменных», «Неопределенный интеграл», «Определенный интеграл», «Ряды». В каждом разделе предоставлен теоретический материал для изучения, примеры и упражнения.

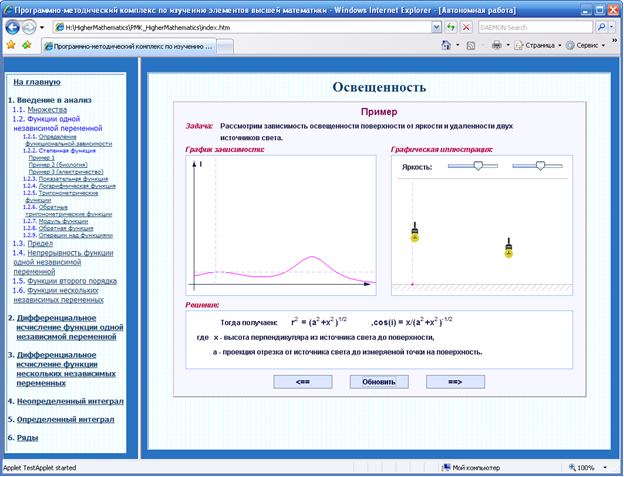
Рис. 1. Фрагмент содержания ПМК

Студент, изучив какой-либо параграф ПМК, может рассмотреть имеющиеся примеры или упражнения, соответствующие его специализации. Например, в параграфе «Функции одной независимой переменной» раздела «Введение в анализ» есть тема «Степенная функция», в которой представлены примеры для студентов биолого-химического и электроэнергетического факультетов (рис. 1). В параграфах ПМК содержится теория (понятия, определения, теоремы) и апплеты с визуализацией преподносимой теории, это апплеты–примеры и (или) апплеты–упражнения. Рассмотрим некоторые из них.

В разделе «Дифференциальное исчисление функции одной независимой переменной» главы «Элементы математического анализа» представлен апплет (рис. 2) демонстрирующий дифференцирование сложной функции. В данном примере субъекту обучения предлагается выбрать правило дифференцирования и функции из таблицы производных.

Рис. 2 Фрагмент примера, иллюстрирующий дифференцирование сложной функции

Также в разделе «Дифференциальное исчисление функции одной независимой переменной» представлен апплет (Рис. 3) для изучения дифференцирования сложной функции. В данном упражнении субъекту обучения предлагается выбрать правило дифференцирования, функции из таблицы производных, заполнить ячейки значения производных. Во время выполнения упражнения прослеживается правильность выполнения заданий, и выводятся необходимые корректирующие сообщения («Правильно», «Неправильно»). В данном упражнении субъекту обучения предлагается выбрать правило дифференцирования, функции из таблицы производных, заполнить ячейки значения производных. Во время выполнения упражнения прослеживается правильность выполнения заданий, и выводятся необходимые корректирующие сообщения («Правильно», «Неправильно»). В конце упражнения выводится сообщение о результате его выполнения (Рис. 4).

В разделе «Дифференциальное исчисление функции нескольких независимых переменных» представлен апплет (Рис. 5) для изучения дифференцирования сложной функции нескольких переменных. В данном упражнении субъекту обучения предлагается выбрать вид функции, правило дифференцирования, функции из таблицы производных, заполнить ячейки значения производных. Во время выполнения упражнения прослеживается правильность выполнения заданий, и выводятся необходимые корректирующие сообщения («Правильно», «Неправильно»). В разделе «Определенный интеграл» представлен апплет (Рис. 6) демонстрирующий вычисление определенного интеграла. В данном примере студенту предлагается выбрать правило интегрирования и функции из таблицы интегралов.

Глава «Элементы линейной алгебры»,  базируется на следующих разделах линейной алгебры: «Матрицы», «Определители», «Операции с матрицами»,  «Собственные значения и собственные вектора линейного преобразования матрицы», «Линейная зависимость», «Решение систем линейных уравнений», каждый из которых разбит на темы - параграфы

В ходе работы с программным комплексом пользователю встретятся апплеты с визуализацией преподносимой теории, а также апплеты – примеры и упражнения для самостоятельного контроля обучающегося, построенные по вышеизложенным принципам.

Применение динамики в программно-методическом комплексе по изучению элементов линейной алгебры не только увеличивает скорость передачи информации учащимся и повышает уровень ее понимания, но и способствует развитию таких важных для специалиста любой отрасли качеств, как интуиция, профессиональное чутье.

После постановки задачи и задания начальных данных студенту предлагается шаг за шагом с подробными пояснениями проследить процесс нахождения ответа. При этом существует связь элементов текста с помеченными данными и используемыми формулами. Применение таких технологий существенно активизирует учебную информацию, делает ее по сравнению с представлением на бумажном носителе более наглядной для восприятия и удобной для усвоения. Рассматриваются  основные виды матриц, а также основные определения элементов матрицы, правила операций с матрицами (рис.7 - 9). Использование динамики позволяет обучаемому  более глубоко изучить данную тему. Это достигается путем предоставления всегда нового примера и его конкретного решения.

Пользователю предоставляется возможность ознакомиться со способами вычисления определителей. Иллюстративные примеры  помогают более быстро и эффективно усвоить материал. Для более глубокого изучения материала данного раздела обучаемому предлагается проследить ход решения примеров каждый раз с новыми исходными данными. Для закрепления полученных знаний обучаемый выполняет упражнения различной сложности, что позволяет ему более прочно закрепить полученный материал.

Глава «Элементы аналитической геометрии  базируется на следующих разделах аналитической геометрии: «Уравнения прямой», «Вектора», «Вычисление площадей фигур», «Уравнение плоскости», «Вычисление объемов фигур», «Элементы Линейной Алгебры с точки зрения Аналитической Геометрии» (рис.10 - 13).

ЗАКЛЮЧЕНИЕ

В докладе представлено некое обобщение традиций и опыта преподавания математики в среде современных информационных технологий, представлены  результаты, полученные автором при  разработке (2001 - 2006 гг.) электронных обучающих систем в  Немецком Центре Искусственного Интеллекта при университете Саарланда (Саарбрюкен, Германия) в системе ActiveMath

  (http://www.activemath.org/Home/Team/viktor)   (http://www.activemath.org).

ActivеMath - это web-базирующаяся, обучающая среда (по математике), разработанная в  рамках проекта LEACTIVEMATH программы FP6-IST Европейского Союза. Эта среда динамически предоставляет интерактивный материал курса, необходимый обучаемому (на различных языках, в том числе русском и английском). Возможности ActiveMath включают персональный подход к предоставленному материалу и характерные для определенного уровня интерактивные элементы, например, они могут быть выбраны согласно их сложности  или  специальности, а также соответственно учебной программе. При этом,  студент, начав обучение, может продолжить его, сменив страну или специальность, в той же системе ActiveMath.

В систему включены курсы «Методы оптимизации» (http://www.activemath.org/Content/OptimizationMethods), «Исследование  операций», элементы курса «Математическая логика» для нескольких специальностей.

Параллельно разрабатывались автономные (вне системы ActiveMath) варианты обучающих систем  по различным математическим дисциплинам: элементы курсов «Математический анализ», «Математическая логика», «Теория графов», «Дифференциальные уравнения ». При этом программно-методические комплексы (ПМК) по курсам  «Теория игр и исследование  операций» и «Методы оптимизации», построенные на основе   компьютерного моделирования учебного процесса, много лет успешно используются в учебном процессе.

Практическое использование показывает, что компьютерное моделирование учебного процесса изучения математики с использованием  информационных технологий является эффективным средством индивидуализации обучения и активизации самостоятельной деятельности студентов, а также оказывает существенную помощь в работе преподавателя.

Автор  готов ответить на вопросы   коллег  и принять участие   в возможной  дискуссии.

Список литературы

1. Горнов А.О. Междисциплинарные аспекты ГГП и инженерной подготовки / А.О.Горнов, Л.А. Шацилло / Материалы всероссийского совещания заведующих кафедрами инженерно - графических дисциплин технических вузов 26-28 мая, Ростов-на-Дону- 2015, С.27-34

2. Ижуткин В.С.. Комплекс обучающих программ по математическому программированию  на основе компьютерного моделирования учебного процесса /Ижуткин В.С.,Токтарова В.И. / Сборник  трудов XIII-й Всероссийской конференции «Математическое программирование и приложения». Екатеринбург. 26 февраля - 2 марта 2007 г.

3. Ижуткин В.С. Компьютерное моделирование учебного процесса изучения математики /. Ижуткин В.С., Токтарова В.И. / Труды 1-ой Международной конференции «Системный анализ и информационные технологии», Переславль-Залесский, 2005, С. 246-249. 

4. Ижуткин  В.С. Принципы построения и реализации обучающих систем по численным методам /. Ижуткин В.С., Токтарова В.И. / Educational Technology & Society 9(1) 2006, ISSN 1436-4522, С. 397-410.

5. Поспелов Д.А. Фантазия или Наука. На пути к искусственному интеллекту. М.: Наука, 1982.

6. Зенкин. А.А.. Когнитивная компьютерная графика /Под ред. Д.А. Поспелова. М.: Наука, 1991. 192с.

Шацилло Людмила Анатольевна (20 февраля 2016 г. 15:25)	Уважаемый Виктор Сергеевич! В применении теорий усвоения ЗУВ в условиях информатизации образования важна оценка уровня усвоения как показатель качества мышления. Основа усвоения учебного материала - это активная мыслительная деятельность обучающихся в новой парадигме равнозначимого учебно-информационного взаимодействия при интеллектуально активном участии: студента, преподавателя и интерактивных источников обучающей информации - в каждой из сфер: познавательной (когнитивной), эмоциональной (аффективной) и психомоторной. В разработанной Б.Ф. Скиннером методике линейного программирования, опирающейся на закон тренировки и закон эффекта и ее развитии - разветвленного программирования для слабых, средних и сильных обучающихся на базе бихевиоризма (невмешательства в мышление обучающегося, управление лишь его поведением), формируются, в основном, психомоторные компоненты структуры личности. Основной недостаток этой теории состоит в отсутствии системности, целостности в восприятии обучающего материала. Т.е. это для работы на конвейере. Не спорим, это тоже надо! В основе ассоциативно - рефлекторной теории усвоения заложено положение о том, что обучение начинается с чувственного познания, и наглядные образы, обогащая сознание, помогают его продвижению к обобщениям на основе сравнения. Практическое воплощение она получила у Я.А.Коменского, выдвинувшего в качестве "Золотого правила" дидактики принцип наглядности. Методика обучения – упражнения, формирующие умение сравнительного анализа. Ассоциативная природа восприятия и мышления дает основания построения различных систем подачи учебных элементов в обучении (mindmapping и т.д.) как средства прочного сохранения знаний в памяти. Но полноценные ассоциации (С.Л.Рубинштейн), могут быть только продуктом аналитико-синтетической деятельности человеческого мышления, выявляющего и усваивающего ассоциации в ходе размышлений. Усвоение же самих ассоциаций - процесс стихийный и неуправляемый, что в практическом обучении точным наукам (и в геометро-графической подготовке также) не всегда может служить надежным приемом в усвоении знаний. С целью активизации осмысления учебного материала в этой теории важно установление корректных логических связей при его представлении для освоения  ЗУВ. Что Вы демонстрируете на слайдах (Надеемся, не статично? По вопросам цветового оформления тоже можно спорить, это очень важно!) Мышление на уровне алгоритмов с использованем концепции алгоритмизации может служить основой для продуктивных уровней освоения, но человеческое восприятие и осмысление объектов и явлений происходит целостно и структурировано, как в гештальт-теории: не сводимо целого к сумме составляющих, не кусочно и пошагово, как это предполагается в теории бихевиоризма. Учебные элементы надо группировать в целостные и логически связные гештальты. Обучающийся «схватывает» такой гештальт одномоментно (симультанно), запечатлевая целостную картину объекта или явления. Принципы этой теория особенно актуальны в развитии правополушарного, образного пространственного мышления, в развитии визуального мышления. С применением медиа при представлении обучающего материала важно владеть технологией группирования гештальта не только в форме лаконичного текста, но и в форме лаконичной группировки графических образов. В когнитивных теориях (информационных, по У. Найссеру, например), в процессе переработки информации центральное место уделяется организации знания в памяти, соотношению вербальных и образных компонентов в процессах запоминания и мышления. Теория поэтапного формирования умственных действий (в рамках психологических в этой группе) относится ее к группе деятельностных. Нам в базовой геометро-графической подготовке (а в математике тоже) жесткость применения какой-то одной теории усвоения не продуктивна. Более естественно комплексное применение механизмов вышеперечисленных теорий. Личностно-ориентированный подход к профессиональной компетентности в информатизированном обучении вызывает необходимость такой  его организации, когда существенная роль в выборе траектории познавательного процесса принадлежит самому обучающемуся в соответствии с доминирующим способом восприятия обучающей информации и механизма ее усвоения. Целесообразнее предоставлять обучающемуся самому решать, выполнять ему упражнения после просмотра учебной информации или переходить к следующей ее порции. Преподаватель должен, учитывая характеристики целевых групп или индивидуумов, иметь набор электронных образовательных ресурсов, реализующих схемы усвоения, отвечающие психологическому типу обучаемых. Вас самого-то профессора учили не по кусочкам, а давали по крайней мере целостно: тему, раздел и т.д. Интегрировали знания мы сами, потому что голова работала. Теперь информатизированная производственная деятельность такова, что многое надо иметь ввиду параллельно, совместно. Значит учить надо уже для облегчения входа в этот процесс и ускорения его параллельного освоения параллельно и интегрированно. Т.е. не широкопрофильно, а полипрофильно, политехнично, политехнологично. Или мы с Еленой Владимировной не правы? И вульгарны в таком понимании процесса инженерной подготовки? Платон нам друг, но истина дороже! А,  в общем, спасибо за доклад!!! Будем на связи теперь, раз нашлись! Работаем же в одном ключе… С искренним уважением Е.В. и Л.А.
Ижуткин Виктор Сергеевич (24 февраля 2016 г. 21:24)	Здравствуйте , Людмила Анатольевна, Перечисленные педагогические теории послужили обоснованием для программной реализации обучающих систем по математике и получения гранта Европейского Союза , они используются комплексно. Разумеется все слайды сделаны с динамических примеров и упражнений, что является главным достоинством  системы. А я учился в Казанском университете по индивидуальному плану, изучал литературу самостоятельно, на  самостоятельное изучение со своей индивидуальной скоростью и направлена  компьютерная среда обучения. С уважением                                Виктор Ижуткин
Шацилло Людмила Анатольевна (24 февраля 2016 г. 23:33)	Добрый вечер, Виктор! Людмила Анатольевна в то время училась КАИ и тоже по индплану, а параллельно в КГУ - численные методы и программирование (тогда все только начиналось, в машинных кодах еще) изучала. Тогда для многих соображающих студентов была главная сложность разложить свою мысль на простые составляющие: мыслили тогда куда более, чем на 7 шагов вперед. А сейчас - по алгоритмам. Идею комплексного применения теорий усвоения и дидактических принципов в blended learning внедряет в своей практике преподавания графических дисциплин Усанова Е.В., о чем пишет и на полях этой конференции и в периодике. Виктор Сергеевич,  против гранта ЕС ничего не имеем против, Только приветствуем. Очень отметили, как прекрасно весь материал свернули, графическим представлением показали (и подсказали студентам) - КАК НАДО.  В Европах и Америках сейчас так учат. М.б. в математике это годится.  А мы на структурно-логических стараемся подавать, с картинками. Просто меня настораживают в вузовском графическом образовании приемы, например, "мини"-заданий для мониторинга и контроля, не формирующие полного представления о качесве мышления студента. Приемы, как у Скиннера. И сейчас все тестирование оформляют также, к сожалению. Напишем лично. Тут очень есть что обсудить. С уважением, Л.А.