ГЕОМЕТРИЧЕСКАЯ ПОДГОТОВКА БАКАЛАВРОВ В УСЛОВИЯХ УХОДА КЛАССИЧЕСКОГО ЧЕРТЕЖА ИЗ СОВРЕМЕННОГО ВЫСОКОТЕХНОЛОГИЧНОГО ПРОИЗВОДСТВА

Уважаемая Людмила Сергеевна! Спасибо за любопытный доклад, к большому моему сожалению не имею под рукой статьи [1]. До сих пор я предполагал, что именно многомерные фигуры и связи проще анализировать (не представлять, представить трехмерному человеку четыре измерения принципиально невозможно) плоские изображения. Отсюда популярность таблиц и графиков, и разных способов снижения размерности (проецирования?!) в многомерном анализе. Подскажите, как наглядно, не пользуясь ортогональными проекциями, изобразить две пересекающиеся комплексные прямые вида A(x+jx')+B(y+jy')+C=0 в пространстве (x, x', y, y')?

Людмила Сергеевна, здравствуйте!

  С одной Вашей точкой зрения полностью согласны и поддерживаем, - сами “не вчера” ,  а  давно  её пропагандируем.  Действительно, ради чего устраивать при наличии 3D моделей  шоковую терапию учащимся, сразу погружая в методологию 2D.  Эти модели сложнее, но речь не идет об  отказе от их изучения и использования вообще , а в каком виде и сколько – это подскажет дальнейший опыт , методическая и проектная практика и потребитель. А наукой НГ останется навсегда и обсуждать это странно. Но в процессе ГПП естественнее идти аналитическим путем ( анализа)  как и при  естественном познании, т.е. начинать моделировать геометрию пространства, начиная с ближайших к нему моделей – физической натуры ( 3D-cкульптуры ), затем 3D геометрических моделей, аксонометрических проекционных и потом системы 2D проекций … И уже на первых моделях стараться решить разнообразные задачи  геометрической подготовки; описания геометрических примитивов ….отношений между ними и т.д. А затем аналогичное в отображении на 2D моделях. Такова наша позиция, в частности и в работе [2], аналогичная  Вашей.

И именно опираясь на эту позицию,  мы не очень согласны с Вами, что из неё вытекает предлагаемая Вами программа.  В чем наглядность n-мерной геометрии  не можем понять. В том, что из общих правил отношения псевдопространственных образов  можно получить выводы, иллюстрируемые наглядными кривыми и поверхностями? Так они ж и породили  термины многомерной геометрии. Мы в принципе не против и общих подходов,  но на завершающей стадии инженерной подготовки как по геометро-графической, математической  и т.д. Возможно мы что не так поняли …  С  уважением, от авторов [2] – Шацилло Л.А., Усановой Е.В. и Горнова А.О.

Здравствуйте, Людмила Сергеевна. Вопрос по программе: Как увязано изложение п.1 с "чёрным ящиком" пакета геометрического моделирования, используемого в учебном процессе?

Опыт моего коллеги, читавшего элективный курс Наглядной геометрии по учебнику Гилберта (Вы почему то не ссылаетесь на него, кроме урезанной цитаты), показал, что не смотря на особенности нашего зрительного восприятия, идёт так же туговато, как и НГ. Может в контингенте в большей степени дело?

Здравствуйте, Людмила Сергеевна. Не совсем понятно, что означает термин "Наглядная многомерная геометрия"? Есть замечательная книжка Гильберт Д, Кон-Фоссен С. "Наглядная геометрия". Вот это действительно геометрия наглядная. А как Вы собираетесь учить студентов, не разбирающихся, по Вашим же словам, в геометрии на плоскости, геометрии пятимерной (это п.2 Вашей программы для студентов-бакалейщиков), которую ни один человек и представить себе не может - ума не приложу.

Теперь по поводу того, что студенты очень хорошо воспринимают так называемые 3D картинки. Это касается всех, кто так или иначе принижает значение начертательной геометрии. Все восхищаются картинками на мониторе, а я думаю - напрасно. Гораздо "нагляднее" будет знакомить студентов с вырезанными из дерева кубиками, конусиками и прочими геометрическими фигурками - ох как наглядно! Даже пощупать можно! Картинками же в компьютере лучше занимать дошкольников в детском саду, но никак не людей, претендующих на ВЫСШЕЕ образование. Те обязаны изучать высшую геометрию, никак иначе.

Людмила Сергеевна, вдогонку такой вопрос: из каких фактическим данных Вы делаете вывод, что эпоха чертежа закончилась? Просто так говорить - это ведь ненаучно.

Уважаемые коллеги! Прошу меня извинить, но по техническим причинам я не могу участвовать в дискуссиях в активном режиме, мои комментарии будут опаздывать во времени.

Прежде всего, обращаю ваше внимание на то, что предлагается «Наглядная инженерная геометрия», а не многомерная геометрия. Последняя представлена в Программе только двумя разделами в строго обозначенных рамками содержанием и является учебной, а не научной дисциплиной, предназначенной для первого уровня высшего образования.

Наглядность подразумевает, прежде всего, изучение трехмерного пространства. Для понимания многомерного пространства нет никакой необходимости созерцать геометрические образы в n-мерном пространстве. Те наглядно понятийные отношения, те наглядные соображения, которые в нем существуют между элементами, делают многие факты анализа наглядными аналогиями. Это позволяет обобщать соображения, действующие при трех переменных к любому их числу. Такой метод наглядного обобщения, не зависящего от аналитического аппарата, позволяет применять геометрические соображения при анализе n-мерного пространства, что и подчеркивается термином наглядная многомерная геометрия (наглядность не в смысле возможности созерцания, а в смысле достижения понимания  (по ак. А.Д. Александрову).

А.А. Байкову. Уважаемый Алексей Александрович! В предлагаемой программе в части по многомерной геометрии содержится только такой материал и его ровно столько, сколько обозначено в содержании раздела 3 и не более того. Проецирование на плоскость и графические решения задач в многомерном пространстве не предусмотрены (это уже математика); иллюстрации даются в виде рисунков. Может быть это Вас разочарует, но так было задумано. Подробнее с материалами содержания, кроме ссылки [1], можно познакомиться на:

Инженерный журнал: наука и инновации, 2014, вып.3
URL: http://engjournal.ru/catalog/pedagogika/hidden/1212.html;

Молодежный научно-технический вестник МГТУ им. Н.Э.Баумана Электронный журнал
http://sntbul.bmstu.ru – здесь предоставлена работа студентов 1-го курса С.А. Лапшиной, А.С. Рожкова. Построение 3D-модели развертки четырехмерного симплекса.

Д.Е. Тихонову-Бугрову.  Уважаемый Дмитрий Евгеньевич! Зрительное восприятие – существенный фактор в обучении графическим дисциплинам. Установленные особенности зрительного восприятия двумерного пространства позволяет нам не винить школу (плохо-де учат), студентов – за нерадивость, отсутствие интереса к учебе (вообще-то, большинство из них добросовестно пытались понять НГ), а нам при обучении НГ принимать во внимание объективно существующие особенности зрительного восприятия, доводящие иногда до психического шока обучающегося.

Что касается взаимоотношения наглядной инженерной геометрии с «черным ящиком» пакета геометрического моделирования то наглядная инженерная геометрия предваряет изучение основ геометрического моделирования. В ней изучают те разделы геометрии форм и взаимодействия предметов пространства, которые составляют суть геометрии как науки. В программе по объемному моделированию на основе полученных знаний решают собственные задачи прикладной геометрии, такие как анализ геометрии технических объектов, анализ моделей прототипов из банка электронных моделей реальных деталей и прочие насущные задачи собственно геометрического моделировния.

А.О. Горнову, Е.А Усановой, Л.А. Шацилло. Здравствуйте уважаемые коллеги! Вам хорошо известно, что НГ была создана Монжем как прикладная наука для обслуживания нужд чертежа. Как научная дисциплина она навсегда вошла в Анналы Науки, и я не знаю почему Вы, Александр Олегович, затрагиваете вопрос о возможности со стороны кого-то (кого?) в этом сомневаться. Но как учебная дисциплина, при современном уровне компьютеризации НГ потеряла актуальность в связи с уходом чертежа из практической деятельности, теоретической основой для которого она была.

Кафедры графики, через предлагаемое заявление геометрии как научного направления деятельности, имеют некую возможность, на мой взгляд, сохранить себя на плаву в этом водовороте перепрофилирования и урезания. Однако, только такая геометрическая дисциплина, как многомерная геометрия, будет смотреться в программах ново, живо и современно. Она может привлечь внимание ищущего свое место в жизни молодого человека, заинтересовав его возможностью познания всего нового и сознанием приобщения к мировым ценностям. Ведь дальше для него может быть магистратура, аспирантура, докторантура.

Н.А. Салькову. Здравствуйте, Николай Андреевич! Вы же всегда заботились о развитии пространственного воображения у студентов. Теперь, когда стало понятным, что силами НГ по объективным причинам сделать это крайне затруднительно, все-таки остался способ (ибо проблема, то, не исчезла), который способен развивать пространственное воображение студентов, т.к. наиболее полно отвечает эволюционному развитию человеческого мозга, приспособленного для восприятия трехмерного окружающего мира – это 3D-электронное моделирование. 3D-электронные модели совсем не картинки. Вы ошибаетесь, когда думаете, что их показывают студентам. Студентов учат самостоятельно создавать объемные модели геометрических фигур и реальных объектов, тем самым приобщая к познанию окружающего мира.

На Ваши соображения по поводу необходимости изучения высшей геометрии в высшей школе, сообщаю следующее: геометрия многомерного пространства является составляющей высшей геометрии. Такой раздел Программы, как задание линий и форм многомерной геометрии рассматривается в учебнике Н.В. Ефимова «Высшая геометрия».

Николай Андреевич, Вы как бы не замечаете главную мысль, проводимую через всю статью – сделать изучение геометрии в её конструктивном преломлении научным направлением деятельности кафедр инженерной графики. НГ здесь не помощник.

Привожу некоторые факты, позволяющие сделать вывод об уходе чертежа из практической деятельности.

1. Официальное заявление фирмы Боинг, прозвучавшее по российскому радио на другой день после катастрофы самолета Боинг над украинской  территорией. В ответ на предположения о возможных причинах гибели самолета фирма сообщила, что все свои самолеты, в том числе и разбившийся Боинг, она изготавливает по самой современной интегрированной CAD/CAM технологии «… без использования чертежей вообще» (цитирую дословно), что по её мнению является гарантией качества и надежности эксплуатируемых самолетов.
2. Доклад В.В. Таланов НГУДАИ, Новосибирск, Куликова С.О. BIM менеджер, Москва «Технология информационного моделирования: опыт работы с памятниками деревянной архитектуры». Доклад сделан на 9-ой Международной научно-методической конференции «Проблемы инженерной геометрии» Москва, МИТХТ, 19-20 октября 2015 г.
   В докладе отмечено, что использование BIM моделирования вместо традиционного чертежа, позволило существенно уменьшить влияние погрешности, обычно вносимой чертежом, на точность и качество работы реставраторов деревянного объекта старины.
3. Комментарии М.А. Пироговой (АВТИМЭИ) на текущей конференции КГП 2016
   Цитирую:
    «… само понятие САПР подразумевает изначально создание трехмерной модели, на базе которой может быть построен любой требуемый вид и чертеж. А не наоборот. Какими циркулями-линейками Вы бы не строили профиль крыла в авиастроении, Вам никогда не добиться за приемлемое время требуемой в авиастроении точности в сотых (0,04 мм) на хордах в 5-10 м. Да ещё и промежутки будете дугами интерполировать? По лекалу? «Ну, не знаю, как с такими крыльями самолеты полетят…»
4. Сотрудники СГАУ (г. Самара) В.И. Иващенко, Л.А. Чемпинский и А.И. Ермаков в рамках проходящей конференции КГП 2016 поделились опытом обучения студентов по-новому мыслить и создавать 3D модели деталей и сложных сборок без использования эскизов и рабочих чертежей деталей, что отвечает сквозному использованию CAD/CAM систем на предприятиях авиационного двигателестроения.

        Людмила  Сергеевна, здравствуйте, как всегда, рад Вас приветствовать!

      Поскольку Вы обратились лично ко мне, то только я пока и отреагирую. Укажите, пожалуйста цитату ( а лучше фрагмент побольше ) , на основании которой мне можно инкриминировать неуважение к  НГ. Как  укажите, - смогу продолжить ответ … Спасибо, с уважением, А.О.

Людмила Сергеевна, у меня возникли пара-тройка вопросов.

1. Каким образом Вы обеспечиваете наглядность трехмерной фигуры и каким образом ее обратимость.

2. Изучая в школе стереометрию, разве не наглядное изображение изучают школьники?

3. Каким образом в Вашей "наглядной геометрии" будет изучаться взаимное расположение, скажем, прямых? В НГ это просто тривиальная задача.

4. А как будут выглядеть касательные и нормали к кривым? В НГ это просто.

5. А как будет выглядеть 5-мерный додекаэдр?

По вопросу Боинга. Что-то часто они стали падать. Может что-то не так в CAD/CAM технологии? А на наших заводах все крылья кроме как при помощи станков с ЧПУ, проверялись еще и лекалами в натуральную величину. И, как я предполагаю, летали не хуже, чем Боинги.

Далее возникает вопрос: зачем же тратить время на модель, если по Вашему же признанию (п. 3 ответа мне), после этого следует изготовлять чертежи?

Уважаемая Людмила Сергеевна, по второй ссылке работы С.А. Лапшиной, А.С. Рожкова, к сожалению, найти не смог. 

Я проглядел статью [1] и вспомнил, что у меня к этой статье были вопросы. В частности, на с. 41 приведена формула расчета размерности пересечения :

r = 2+3-2=1 (линия) - должно быть равно 3?

В докладе вы ссылаетесь на статью [1]: "была опробована и подтверждена экспериментально возможность встраивания наглядной геометрии и многомерного пространства", но в статье [1] я не увидел ни одного наглядного изображения многомерных фигур, кроме известной развертки тессеракта. Сомневаюсь, что эта развертка наглядно демонстрирует свойства оригинала. Большая часть иллюстраций к статье [1] - именно ортогональные проекции, которые, в соответствии с вашими тезисами, лишены "одной из наиболее привлекательных особенностей геометрии, а именно наглядности изображения". Я позволю себе привести некоторые.

На рис. а и б для указания положения секущей плоскости использованы ортогональные проекции (более наглядны?!), а не аксонометрии. На рис. г, д, ж, з также выбраны ортогональные проекции, и аксонометрические их только дополняют (рис. е, и), причем наглядность последних вызывает у меня сомнения. Сравнительно наглядными я считаю лишь рис. в, к, л, изображающие многогранники. Причина - особенности выпуклых многогранников, а не достоинства аксонометрий. Перпендикулярность высоты основанию ABC в пирамиде на рис. (л.б) неочевидна (не наглядна?). Методика решения графических задач на центральных и параллельных аксонометриях многогранников есть у Вольберга (Лекции по начертательной геометрии), Четверухина (Аксонометрия) и др.

Таким образом, я совсем запутался и не понял, какой смысл вы вкладываете в слово "наглядность". Имея в виду объективную и, очевидно, поддающуюся измерению оценку, например здесь:

>> ...такая объективная причина, как потеря наглядности изображения.

У меня создалось ощущение, будто наглядность=трехмерность модели. Н.С. Кузнецов в статье "К вопросу о наглядности изображений" (Начерт.геом. и инж.графика: сборник науч.-метод.статей. Вып. 1. 1973) отмечает, что наглядность зависит "от жизненного опыта, профессии, возраста и т.д. познающего человека". Т.е. одна и та же модель может становиться более наглядной по мере приобретения опыта.

>> Когда вместо трехмерного объекта обучающемуся на уровне зрительного восприятия предлагается двумерное изображение, это приводит к возникновению психологического барьера для восприятия

Когда к нам обращаются на незнакомом языке, это, пожалуй, тоже "приводит к возникновению психологического барьера", и преодолевается "лишь путем запоминания в памяти через монотонное обучение". Следует ли человечеству отказаться от изучения иностранных языков?

Несомненно, "современные компьютерные средства обеспечивают высокую наглядность при 3D-электронном моделировании объекта за счет создания трехмерных компьютерных моделей", но лишь по одной причине - изоморфности моделируемого пространства и пространства модели. Станет ли 3D-электронная модель нагляднее плоского графика функции y=f(x)? Станет ли нагляднее плоской блок-схемы? 

Станет ли 3D-электронная модель четырехмерной фигуры нагляднее плоской модели четырехмерной фигуры? Опыт многомерного анализа данных убеждает нас в обратном.

Я. Нильсен в книге о проектировании интерфейсов [Веб-Дизайн, 2003] отмечает, что «на практике следует отдавать предпочтение двумерной» графике, так как, в частности, «особое внимание управлению трехмерной моделью» мешает «выполнению основных задач». Только в 3D-конструировании основная задача "трехмерна". В остальных случаях анализ изображения человеком будет сопровождаться декодированием, которое тем проще, чем проще изображение.

Таким образом, вывод о том, что "уход чертежа, как в его классическом, так и в электронном варианте исполнения из практической деятельности снимает задачу научить студентов составлению и чтению чертежа", делается на основе неверных посылок.

Наконец, так ли уж "наглядна" трехмерная электронная модель сама по себе?

- стенки корпуса закрывают всю внутреннюю начинку. Для того, чтобы заглянуть внутрь, необходимо снимать детали или рассекать изделие, притом какая-нибудь часть все равно будет чем-нибудь закрыта; ни один из элементов не виден в натуральную величину, если только не активировать какой-нибудь ортогональный вид. На чертеже все виды, разрезы и сечения представлены одновременно. Что в этом случае называть "наглядностью"?

Еще пара цитат Нильсена: "в результате эволюции зрение человека было адаптировано для передвижения по равнине, а не по деревьям", "абстрактные информационные пространства ... плохо поддаются реализации в виде трехмерных моделей", так, если пространство имеет "100 измерений, его трехмерная визуализация означает отбрасывание 97 измерений вместо 98" (для плоской); трехмерный интерфейс переносит недостатки объектов реального мира в компьютерную среду, задача которой - "сделать такие элементы лучше, чем в реальной жизни", так, человеку в реальном мире приходится переходить от объекта к объекту, огибать препятствия, перекладывать предметы, компьютерная система "позволяет мгновенно перемещаться к выбранному пункту назначения".

Преимущества 3D-моделирования перед черчением не вызывают сомнения, но по причинам, как мне кажется, не имеющим отношения к наглядности, а именно: 1) простоте получения любого дополнительного изображения, 2) простоте внесения изменений, 3) возможности использования электронной модели на других этапах проектирования и подготовки производства. Именно это подтверждает справедливость вашего замечания об "уходе чертежа из современной практической деятельности", а не недостатки чертежа как такового.

Наконец, "определяющим достоинством классического чертежа" стала, пожалуй, не его обратимость сама по себе (обратима и аксонометрия, и сопряженные центрально-ортогональные проекции), но обратимость + возможность решения прикладных задач (не только в машиностроении), компенсирующая недостаток "наглядности" простотой применения формальных методов. Фактически, решить задачу начертательной геометрии может любой студент независимо от его пространственного воображения, если усвоит алгоритмы. Многомерное моделирование вступает в ту область, где человеческий опыт (пространственное воображение) уже ничем не может помочь, на передний план выступают именно формальные методы. В этом отношении "классический чертеж" вовсе не потерял своих достоинств.

Я так подробно остановился на этом, потому что в п.1 программы вы указываете - "Предмет, назначение, наглядность".

Теперь, собственно, о наглядной геометрии. Цель и задачи книги Гильберта и Кон-Фоссена состояли в том, чтобы, отказавшись от чрезмерных (абстрактных) аналитических выкладок, представить в образной форме "грандиозные систематические построения алгебраической геометрии, римановой геометрии и топологии".

В чем цель и задачи предлагаемого курса, а вернее той части, которая называется "наглядной инженерной геометрией", "наглядной многомерной геометрией"? 

Термин "инженерная геометрия" (прикладная геометрия) появился в 60-х гг и объединил начертательную геометрию, номографию, графические и графоаналитические методы, инженерное черчение (Четверухин Н.Ф. Прикладная геометрия и некоторые вопросы ее развития // Прикладная геометрия и инженерная графика. Вып. VIII. 1969). Термин "многомерная геометрия" довольно широк, но, как часть прикладной геометрии, многомерная геометрия включает "теорию обратимых чертежей n-мерного пространства", "частные виды обратимых чертежей", "многомерную аксонометрию", "НГ многомерных неевклидовых пространств", "геометрические методы исследования многокомпонентных систем" (Труды Моск.науч.-метод. семинара по НГ и ИГ. Выпуск 3. Труды МАИ. Выпуск 242. 1972). Содержание паспорта специальности 05.01.01 "Инженерная геометрия и компьютерная графика" приведено в докладе С.И. Роткова, в частности, многомерная геометрия тесно связана с номографией.

Предлагаемый курс состоит из двух плохо связанных между собой частей - многомерной геометрии, которую вы собираетесь иллюстрировать на примере трехмерных моделей, и, собственно, трехмерного геометрического моделирования.

В первой же части упоминаются "координатная система и преобразования координат и пространства", которые, очевидно, относятся к аналитической (т.е. не наглядной) области геометрии.

Уточнение "Многогранники в n-мерной геометрии. Наглядно – геометрический подход" не помогает, поскольку ни в статье [1], ни в докладе нет ни одного наглядного представления многомерного многогранника. В целом, у меня создалось впечатление, что эта часть курса соответствует книге С.М. Куликова "Введение в начертательную геометрию многомерных пространств". Осталось не вполне ясным, как 3D-электронные модели помогут студентам в многомерном моделировании.

Вы основываетесь на предположении, будто "взгляды на абстрактный многомерный мир ... доступны к восприятию наглядным способом изложения с проверкой основных постулатов через частные реализации на компьютерных моделях трехмерного пространства". Следуя методу индукции, можно было бы сказать и так: доступны с проверкой основных постулатов через частные реализации на моделях двухмерного или даже одномерного пространства, однако, это не работает: пересечение прямой с треугольником на плоскости, несмотря на "обобщение законов", осуществляется иначе, чем пересечение плоскости с тетраэдром в пространстве.

В разделе "Поверхности. Обзор некоторых видов поверхностей...", судя по всему, планируется отказаться от практического построения линейчатых поверхностей общего вида (эллиптического гиперболоида, поверхностей Каталана, коноидов и др.), моделирование которых требует трудоемкого построения каркаса.

Также вызывает вопрос содержание разделов "Позиционные задачи..." и "Метрические задачи..." в отношении "элементов пространства n измерений". В комментарии вы отметили, что "это уже математика (иллюстрации даются в виде рисунков)".

В целом, мне кажется, еще требуют уточнения цели и задачи курса, понятие "наглядности", понятие инженерной геометрии, связь наглядности и многомерной геометрии. Клубок понятий, терминов и технологий в настоящее время мешает увидеть новую дисциплину, как нечто целое. Со стороны человека "в теме" видится что-то лоскутное.

С уважением и наилучшими пожеланиями, Бойков

Здравствуйте Николай Андреевич!
Отвечаю Вам в порядке поступивших вопросов.
• Обратимость обеспечивается математическим моделированием, ибо с трехмерной  модели можно получить информацию о координатах любой точки на поверхности, а  наглядность – визуально на экране компьютера геометрическим моделированием.
• В школьной стереометрии изображения фигур изучаются по их рисункам в  наиболее наглядном ракурсе. Но это не чертеж, и не 3D модель.
• Примеры решения позиционных и метрических задач приведены в статье [1]  опубликованной в журнале ГиГ. Но обращаю Ваше внимание, что хотя, это все  3Dмодели фигур, в статье на бумаге могут быть представлены только плоские  изображения в одном ракурсе (что подтверждает потерю наглядности при  проецировании на плоскости), но поскольку, изначально строились 3D модели,  просмотр их на компьютере за счет его возможностей повышает наглядность  изображения. Особенно эффектны пересечения поверхностей (теорема Монжа),  когда поверхности окрашены в разные цвета. В этой же статье на рис. 5  построены касательные, касательные плоскости и нормали к ним; там же даны  пояснения. Вообще построение в пространстве и на плоскости – совсем разные  задачи. Цель сравнить способы решения – не ставится.
• Пятимерный додекаэдр, будучи правильным многогранником, в пространстве с  размерностью n>4 не существует.
• При изготовлении отечественных самолетов в былые времена затрачивалось  большое количество ручного труда для обеспечения профиля согласно чертежу, что определяло высокую стоимость их изготовления. Но денег государство не  жалело; теперь работодатели-собственники научились считать экономический  эффект.
• В п.3 ответа Вам помещено не мое признание, а дословно цитируется М.А.  Пирогова. Свое мнение я излагаю в своей статье.

Здравствуйте Алексей Александрович!
• В формулу (3) на стр. 41 [1] действительно закралась досадная опечатка.  Спасибо, что Вы на неё указали, очень досадно. Согласно (2) формулу (3) [1]  следует читать так:
                       r= p₁+p₂–n=2+2–3=1 (линия) (3)
• Упрекаете, что мало сделали, действительно виноваты, но не успеваем. Со студентами, кроме развертки четырехмерного куба, сделали развертку  четырехмерного симплекса и четырехмерного октаэдра. Сейчас печатаем их на 3D  принтере. Планируем публиковать в апреле.
• Не вижу необходимости созерцать сами фигуры в многомерном пространстве. А  если эта задача встанет лично перед Вами, то Вы и будете её решать. Я  действую в рамках написанной мною Программы.
• Вы ошибаетесь, если думаете, что в [1] приведены результаты ортогонального  проецирования или прямоугольная аксонометрия. Это все – 3D модели в разных  ракурсах. Но при публикации на бумаге (читайте плоскости) теряется  наглядность: всего один единственный ракурс, черно-белое исполнение, без  динамики, наличие ограничений по количеству иллюстраций и качеству их  воспроизведения. Но, поскольку, в действительности, это все 3D модели,  студент, рассматривая их на компьютере, использует все возможности  компьютера и изучает очень наглядные изображения. Кстати, пересечение двух  поверхностей, окрашенных в разные цвета (теорема Монжа) чрезвычайно эффектно  выглядит на экране компьютера.
• Геометрическое изложение n-мерной геометрии, не зависящей от  аналитического аппарата, впервые было сделано на примере правильных  многогранников многомерного пространства. Поэтому я включила эти темы в п.п. 3.3 и 3.4 Программы. Многогранники вообще традиционны в геометрии из-за  наглядности при изучении, поэтому не надо им ставить это в вину и отказываться от них.
• Интересен Ваш вывод по поводу разверток многомерных фигур: не знаю, не  видел, не изучал, но сомневаюсь – прямо как в лучших традициях прошлого  века.
• Наглядное изображение, действительно, находится в кругу привычных образов,  доставляемых нашими органами чувств. Но безусловные и условные рефлексы  никто не отменял. Такова действительность нашего нахождения в реальном  пространстве; но нас тянет в неизвестное.
• Я представила не научную теорию, а учебную программу для первого уровня  обучения в высшей школе с весьма ограниченным (надо думать) временем  обучения. Поскольку представлена только Программа (ее содержание пока  остается за скобками), каждый волен ее трактовать по своему усмотрению. Я  надеюсь, что Вы представите не лоскутный материал, а вполне законченную  работу.
Спасибо за внимание. Желаю успеха!

Здравствуйте Александр Олегович!
Ваша претензия ко мне – полнейший абсурд, к которому я не имею никакого  отношения. Но раз Вы это сами придумали, то сами и ищите тот дословный текст  с любым количеством цитат, из которого родилась эта неправда. При таком  уважении к Вам всякая неправда, идущая от Вас, для меня оскорбительна.

Людмила  Сергеевна, здравствуйте!  Согласитесь,  из приведенных ниже цитат  скорее следует,   что “у Вас  есть мнение, но Вы  с ним  согласны”, а претензии при этом предьявляете  мне. Удивлен, но не обижаюсь …Читайте еще раз …  

    Это из Вашего, Л.С.? ..

1. Как научная дисциплина ( НГ ) она навсегда вошла в Анналы Науки, и я не знаю почему Вы, Александр Олегович, затрагиваете вопрос о возможности со стороны кого-то (кого?) в этом сомневаться. Но как учебная дисциплина, при современном уровне компьютеризации НГ потеряла актуальность в связи с уходом чертежа из практической деятельности, теоретической основой для которого она была.

Людмила  Сергеевна, здравствуйте, как всегда, рад Вас приветствовать!      (Это я  !…)

    2)  Поскольку Вы обратились лично ко мне, то я и отреагирую. Укажите, пожалуйста цитату (а лучше фрагмент побольше), на основании которой мне можно инкриминировать неуважение к  НГ. Как  укажите, - смогу продолжить ответ … Спасибо, с уважением, А.О.

  Здравствуйте Александр Олегович ! ( это Вы, Л.С. ?(А.О.),                                                                        3) Ваша претензия ко мне ( какая,в чем ?А.О.) – полнейший абсурд, к которому я не имею никакого  отношения. Но раз Вы это сами придумали ( что?А.О.), то сами и ищите тот дословный текст  с любым количеством цитат, из которого родилась эта неправда( какая?А.О.). При таком  уважении к Вам всякая неправда, идущая от Вас, для меня оскорбительна.

     Как говориться, Людмила Сергеевна , – остаётся только  “развести   руками”, в голову не лезет .  А.О. ….

Алексей Александрович, а в действительности Вы как думаете - чертеж уходит из жизни? И еще вопрос - начертетльную геометрию хотят выгнать из пределов высшего образования исключительно за то, что она якобы является лишь прислужницей чертежа. Вы на этот посыл ничего не написали.

С уважением, Сальков.

Уважаемый Николай Андреевич, "этот посыл" не заслуживает ответа, в принципе.

Мое мнение - чертеж не уйдет, не просто "еще долго", а, думаю, в обозримом будущем или вообще, как не уходят шариковые ручки и бумага, как бумажные книги и еще многое. Очевидно, часть чертежа займут технологии "3D электронного моделирования", часть - трансформируется в электронный чертеж, который будет значительно удобнее бумажного - станет интерактивным, динамическим, многомерным и т.п., думаю, останется и бумажный чертеж, в конце концов, ни один самый большой монитор не сравнится с листом формата А0 или хотя бы А1. В конце концов это просто красиво.

С другой стороны, попал ко мне в руки недавно учебник Рынина 1939 года (появится время, выложу там же, с Извольским) - ведь не сравнишь с нынешним Королевым. Ведь это не кто-то "извне" сделал начертательную геометрию "прислужницей", свои же. Измельчали учебники, задачники (ведь все это не нужно для того, чтобы построить чертеж!) - столько всего порастеряли. Теперь пожинаем.

С уважением, Бойков.

Здравствуйте, Людмила Сергеевна. 

В этот раз я поздно зашел на конференцию и с радостью увидел Ваш доклад. Мы единомышленники, практически, во всем, что связано развитем наших кафедр, с ролью 3d. Но есть и вопросы:

1. В Вашей программе мне непонятен акцент на многмерную геометрию. Как это связано с 3d? Есть ли Ваши работы на эту тему? 

2. Насколько мне известно, в МВТУ не приветствуют 3d в учебном процессе. Или я не прав? Вы там одна воюете или есть коллеги-единомышленники?

3. В связи с моими текущими задачами меня особенно заинтересовал пункт 8 Вашей программы о 3d принтере и практике создания макетов по их 3d электронным моделям.

Поскольку Вы не указали закрытый канал для общения, то открыто обращаюсь с просьбой. Я буду в Москве на конференции Инфорино-2016, в МЭИ, 11-15 апреля с.г. Извините за назойливость, но я был бы признателен прийти к Вам в МВТУ, познакомиться  и пообщаться на общие темы, в частности о 3d принтере.  За мной - подарок: два моих последних учебника по 3d в учебном процессе (год издания 2015 и 2016). На вякий случай : heifets@yandex.ru

С уважением. А.Л. Хейфец

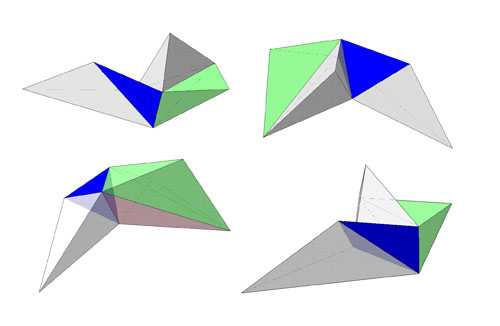
Уважаемая Людмила Сергеевна, прошу прощения за въедливость, но мне хочется кое в чем разобраться до конца.

Хоть я и "не знаю, не  видел, не изучал", но многомерная геометрия меня интересует, кстати, благодаря Геннадию Сергеевичу Иванову, который на курсах повышения квалификации в МВТУ прочитал нам (слушателям) лекцию о многомерной геометрии. Г.С. решал задачу пересечения прямой с гиперплоскостью, не помню, то ли в 4х-, то ли в 5ти- мерном пространстве, используя для этого ортогональный чертеж. До того случая я многомерной геометрией не интересовался, а после лекции у меня в руках вдруг оказался простой и эффективный инструмент для исследования многомерных фигур и решения некоторых задач - хорошо знакомый мне комплексный чертеж, никак не изменившийся по сравнению с 3D, кроме появления еще одной проекции. И тут Ваш доклад с многомерной геометрией в 3D.

Я самым честным образом пытаюсь понять Ваши основные тезисы. Я тут набросал на досуге пример. Дана трехмерная развертка четырехмерной фигуры общего вида (искал ракурс как можно выгоднее). Что можно сказать об исходной фигуре?

Что нам это дает? Какие это открывает перед нами возможности? Можем ли мы построить произвольное трехмерное сечение? Двухмерное? Как мы будем развертывать пятимерную фигуру, если уже развертка сама будет четырехмерной?

С уважением, Бойков.

Людмила Сергеевна, спасибо за доклад. Дискуссия, которая сопровождает его, указывает что тема свежая и новая. Желаю удачи в ваших разработках. С уважением Елена Анатольевна.

Здравствуйте Елена Анатольевна! Какой приятный и неожиданный подарок - знакмство с Вами. Спасибо за внимание.

Здравствуйте Алексей Александрович! Не всякий случайный набор треугольников является разверткой какой-то фигуры. В [1] на примере построения развертки четырехмерного куба можно познакомиться с подходом и теорией построения разверток n-мерных многогранников. Есть ссылка на литературу. После освоения этого материала Вы сами оцените возможности метода и поймете, создали ли Вы развертку или нет.

Заветная мечта Г.С. Иванова соединить воедино аналитическую и начертательную геометрии в любом пространстве. Это чисто научные исследования, а для учебной программы многомерная начертательная геометрия совсем не годится. Но это вовсе не значит, что Вы лично не можете ею заниматься.

Мой подход к учебной программе: 1) сделать геометрию научным направлением деятельности кафедр ИГ; 2) изучать наглядную инженерную геометрию в модельном пространстве компьютера; 3) познакомить студентов в популярной форме с многомерной геометрией через расширение понятия пространства от трехмерного до многомерного. Это знание ново и современно и направлено на перспективу развития у инженеров научного интереса в условиях ускорения научно-технического прогресса.

Здравствуйте Александр Львович! Для сохранения статуса кафедр ИГ считаю необходимым сделать геометрию научным направлением их деятельности.

С этой целью предложена наглядная инженерная геометрия с конструкторским уклоном. Действительно, два раздела в ней отданы многомерной геометрии. На мой взгляд, расширение понятия пространства от трех- до многомерного сегодня воспринимается ново, свежо и современно. Это дает кафедрам ИГ некую возможность сохранить себя на плаву в этом водовороте перепрофилирования и урезания.  

Сегодня в программу курса компьютерной графики на нашей кафедре включены лабораторные работы по построению моделей и созданию чертежей деталей с использованием системы автоматизированного проектирования Autodesk Inventor. Авторы разработки В.Н Гузненков и П.А. Журбенко. 

Людмила Сергеевна, так можно познакомиться... с методикой преподавания п.8: 3d принтер..., о чем я просил в предыдущем своем обращении к Вам. Или, если я Вас правильно понял, советуете обратиться к Гузенкову В.Н.

С уважением. А.Л. Хейфец

Всем глубоко уважаемым оппонентам!

Коллеги! Чтобы понять какой студент придет к нам уже в ближайшем будущем, считаю необходимым познакомиться со статьей "Использование ракетно-космической компоненты в графической подготовке системы школа-вуз". Авторы: Абросимов С.Н., Пахомова О.Ф., Тихонов-Бугров Д.Е., Уханёва В.А.

Итак, это будет молодой человек, довольно свободно владеющий компьютером и умеющий создавать 3D-модели изделий высокотехнологичного производства.

Что предложит ему кафедра "Инженерная графика" на первом уровне подготовки по существующей сегодня программе обучения: теорию построения двух- или трехкартинного чертежа Монжа и научит читать и создавать чертежи. Уже сегодняшний студент спрашивает: для чего надо сначала создать чертеж, если я умею и хочу сразу строить 3D-модели.

С такой учебной программой, на мой взгляд, кафедры ИГ не имеют будущего.

В условиях современной реалии ухода чертежа из практической деятельности и реагируя на ведущие тенденции и потребности инженерной подготовки, кафедры ИГ неизбежно должны пересмотреть существующие программы обучения. В основу предлагаемой "Наглядной инженерной геометрии" положены: представление современной геометрии о наглядном изображении форм геометрических объектов в их электронной разновидности и отношений между ними, а также представление о многомерности пространства. Такой подход позволит через сохранение наглядной геометрии как научного направления деятельности для кафедр ИГ занять освобождающуюся от НГ нишу в современном высшем техническом образовании.

Соколова Л. С. 

Александр Львович, Гузненков В.Н. здесь не причем.

Людмила Сергеевна!

Наконец-то начинаем приходить к консенсусу, правда, с разных сторон. Тем не менее, прогресс в наших общих делах налицо. Полностью согласен с вашим последним тезисом, тем более, что пишу об этом в разных формах не первый год. Только через научную деятельность кафер геометрии и графики можно добиться прогресса в развитии геометро-графической подготовки студентов, только через ориентацию кафедр на триединство учебных дисциплин и информационных технологий. Только с этих позиций надо рассматривать подход к реформированию учебных программ. Кстати, предлагаемый вами проект рабочей программы можно взять за основу и с некоторыми доработками и изменениями использовать в учебном процессе.

С увжением, С.И.Ротков.