МНИМЫЕ ЭЛЕМЕНТЫ В АЛГЕБРЕ И ГЕОМЕТРИИ

Рассмотрены проективные алгоритмы построения кривых второго порядка, заданных смешанным набором действительных и мнимых элементов. Составленные графические алгоритмы позволяют определять метрику конического сечения, инцидентного не только действительным, но и попарно комплексно сопряженным мнимым элементам (мнимым точкам и мнимым касательным), заданным эллиптическими инволюциями на прямой или в пучке прямых. Решена задача построения конического сечения, заданного пятью точками, из которых две мнимые. Также рассмотрена задача построения кривой второго порядка, заданной точкой и четырьмя мнимыми касательными. Для решения задач используются геометрически точные графические алгоритмы, исключающие необходимость выполнения каких-либо алгебраических расчетов. Метрика искомой кривой определяется с помощью специализированной компьютерной программы. В программном алгоритме используются только два графических примитива – прямая линия и окружность, поэтому точность определения метрики равна точности представления простейших геометрических объектов в базовом графическом пакете.

1. В области комплексных чисел алгебраическое уравнение F(x)=0 степени n имеет ровно n корней. Этому уравнению ставится в соответствие алгебраическая кривая n-го порядка y=F(x), пересекающаяся с осью x строго в n точках – действительных или мнимых. Очевидно, мнимые точки недоступны при геометрических построениях.

2. Произвольное коническое сечение r устанавливает на произвольной прямой x инволюцию сопряженных точек σ(A-A1, B-B1,…). Точки U, V пересечения коники r и прямой x – двойные (самосопряженные) точки этой инволюции (рис. 1, а). Все конические сечения, проходящие через точки U, V, устанавливают на прямой x одну и ту же инволюцию σ. Справедливо и обратное утверждение: если какое-либо коническое сечение устанавливает на прямой x инволюцию σ, то оно инцидентно точкам U, V.

3. Пусть требуется построить конику, проходящую через заданные точки 1, 2, 3 и через действительные точки U, V. Построение коники “по пяти точкам” не вызывает затруднений. Усложним задачу: будем считать, что доступны для конструктивных построений только соответственные пары точек A-A1, B-B1,… инволюции σ, а двойные (самосопряженные) действительные точки U, V этой инволюции условно недоступны (рис. 1, б). Такое упражнение следует считать подготовкой к решению задач с участием безусловно недоступных мнимых элементов.

4. Через пару заданных точек (например, через 1 и 2) проведем прямую и отметим точку T ее пересечения с прямой x. Найдем точку T1, сопряженную с точкой T в инволюции σ. Поляра t точки T должна пройти через точку T1 и через точку G – четвертую гармоническую к точкам 1, 2, T. Полюс T и поляра t – центр и ось гармонической гомологии, преобразующей искомую конику в себя. В этой гомологии находим точку 4, соответственную заданной точке 3 (рис. 1, в).

5. Чтобы найти еще одну (пятую) точку искомой коники, отметим точку F пересечения прямой 1-4 с прямой x и найдем точку F1, сопряженную с точкой F в инволюции σ. Поляра f точки F проходит через F1 и через точку H – четвертую гармоническую к точкам 1, 4, F. Полюс F и поляра f – центр и ось гармонической гомологии, преобразующей искомую конику в себя. В этой гомологии находим точку 5, соответственную данной точке 1. Через точки 1, 2, 3, 4, 5 проводим искомое коническое сечение (рис. 1, г).

6. Рассмотренный алгоритм не зависит от типа инволюции σ, которая может быть как гиперболической, так и эллиптической.

Построение кривой второго порядка, инцидентной пяти точкам, две из которых – мнимые

7. Требуется построить коническое сечение, проходящее через заданные точки 1, 2, 3 и через мнимые точки U, V пересечения коники r с прямой x (рис. 2, а). Коника r устанавливает на x эллиптическую инволюцию σ(A-A1,…) с мнимыми двойными точками U, V. Любое коническое сечение, устанавливающее на x инволюцию σ, будет обязательно проходить через мнимые точки U, V.

8. Поэтому задачу можно сформулировать следующим образом: построить конику, проходящую через точки 1, 2, 3 и устанавливающую на прямой x заданную инволюцию σ. В этой формулировке не только отсутствует упоминание о мнимые элементах, но становится несущественным, о какой инволюции идет речь – гиперболической  или эллиптической.

9. Напомним, что алгоритм, изложенный в п. 4, 5, не зависит от типа заданной инволюции σ. Поэтому его можно применить для решения поставленной в п. 7 задачи.   

10. Через пару заданных точек, например, через 1 и 3, проведем прямую и отметим точку T ее пересечения с прямой x (рис. 2, б). Найдем точку T1, сопряженную с точкой T в инволюции σ. Поляра t точки T проходит через точку T1 и через точку G – четвертую гармоническую к точкам 1, 3, T. Полюс T и поляра t – центр и ось гармонической гомологии, преобразующей искомую конику в себя. В этой гомологии находим точку 4, соответственную заданной точке 2 (см. рис. 2, б).

11. Чтобы найти еще одну (пятую) точку искомой коники, отметим точку F пересечения прямой 1-2 с прямой x и найдем точку F1, сопряженную с точкой F в инволюции σ (рис. 2, в). Поляра f точки F проходит через F1 и через точку H – четвертую гармоническую к точкам 1, 2, F (на рис. 2, в точка H условно не показана). Полюс F и поляра f – центр и ось гармонической гомологии, преобразующей искомую конику в себя. В этой гомологии находим точку 5, соответственную точке 4. Через точки 1, 2, 3, 4, 5 проходит искомое коническое сечение e (см. рис. 2, в). Коники r и e устанавливают на x одну и ту же эллиптическую инволюцию σ, в которой произвольной точке B ряда x отвечает точка B1 этого ряда (рис. 2, г). Задача решена.

12. Таким образом, для построения дополнительных точек искомой коники, “компенсирующих” принципиальную недоступность мнимых точек  U, V, потребовалось всего лишь провести несколько прямых (рис. 2).

13. Для окончательного решения задачи используется проективно-синтетический алгоритм и программное средство построения главных осей коники, заданной пятью действительными точками [1, 2]. Существенно, что как в алгоритме, так и в программе нет никаких алгебраических расчетов, а для геометрических построений используются лишь два простейших графических примитива – прямая линия и окружность. Следовательно, построение главных осей коники, инцидентной двум мнимым и трем действительным точкам, выполняется геометрически точно – циркулем и линейкой.

14. Рассмотренная задача может быть решена алгебраически. Решая совместно уравнения окружности r и прямой x, находим комплексные координаты точек U,V их пересечения (см. рис. 2, а). Подставляя в общее уравнение  кривой второго порядка F(x, y)=0 координаты точек 1, 2, 3, U, V, получаем систему пяти линейных уравнений, из которой определяем значения пяти коэффициентов уравнения F(x, y)=0. Присутствие комплексных чисел в главном определителе и в минорах системы линейных  уравнений не затрудняет решение, так как мнимые части комплексных чисел взаимно уничтожаются. Приводя найденное уравнение F(x, y)=0 к каноническому виду, получаем главные оси искомой коники.

15. Алгебраический способ решения выглядит не слишком привлекательно в сравнении с проективно-синтетическим. Более того, можно предположить, что алгебраический способ менее точен при реализации на компьютере, чем проективный. Дело в том, что вычисление определителя матрицы – совсем не простая процедура. Если коэффициенты определителя сильно различаются (на порядки), то для обеспечения точности приходится применять специальные меры (нормирование и пр.), которые могут и не дать ожидаемый эффект.

Графическое представление мнимых элементов

16. Инволюция σ(A-A1, B-B1,…) на прямой x может считаться вещественным представителем двойных точек этой инволюции. Две пары соответственных точек инволюции σ полностью заменяют ее двойные точки при выполнении конструктивных построений. Например, с помощью соответственных точек эллиптической инволюции σ была найдена коника, проходящая через мнимые, принципиально недоступные, двойные точки этой инволюции (см. п. 7…13 и рис. 2).

17. Поэтому для изображения мнимых точек достаточно указать определитель эллиптической инволюции σ. Следуя А.Г. Гиршу [3, 4], определитель инволюции может быть задан “маркером” x(O, L), состоящим из прямолинейного ряда x и точки Лагерра L, из которой инволюция σ проецируется на прямую x ортогональным пучком прямых. Основание O перпендикуляра, опущенного из L на x – центр инволюции σ (рис. 3, а). Маркер x(O, L) считают графическим изображением пары комплексно сопряженных мнимых точек.

18. Итак, мы научились изображать мнимые точки и использовать их в конструктивных построениях. Но как быть с мнимыми прямыми? Где эти прямые? Кто их видел?

19. Согласно принципу двойственности, ряду точек второго порядка (коническому сечению) двойственно соответствует пучок прямых второго порядка (множество касательных к коническому сечению). Ряд второго порядка содержит как действительные, так и мнимые точки. Пучок прямых второго порядка содержит как действительные, так и мнимые прямые (мнимые касательные к коническому сечению). Интересно отметить, что мнимых точек и мнимых касательных у любой коники на порядок больше, чем действительных точек и касательных.

20. Продолжим двойственные рассуждения. Напомним, что произвольная коника e устанавливает на произвольной прямой строгий порядок: инволюцию сопряженных точек (см. п. 2). Такой же строгий порядок (инволюцию сопряженных прямых) коника e устанавливает в пучке прямых с вершиной в произвольной точке V: произвольной прямой a пучка V соответствует прямая a1 этого же пучка, проходящая через полюс A прямой a в поляритете с ядром e.

21. Если точка V расположена вне коники e, то в пучке V устанавливается гиперболическая инволюция с двумя действительными самосопряженными прямыми u, v (действительными касательными к конике e). Если точка V внутри коники – тогда в пучке V получаем эллиптическую инволюцию ρ с двумя мнимыми самосопряженными прямыми (мнимыми касательными к конике e).

22. Определитель эллиптической инволюции ρ может считаться графическим изображением ее мнимых самосопряженных прямых. Следуя А.Г. Гиршу, определитель задают прямоугольной “маркой” V(h-h1, d-d1), содержащей главные h, h1 и ортогональные d, d1 взаимно сопряженные направления в пучке V (рис. 3, б). Марку V(h-h1, d-d1) считают графическим изображением пары мнимых прямых, пересекающихся в действительной точке V.

23. Все конические сечения, касающиеся прямых u, v, устанавливают в точке V пересечения прямых u, v одну и ту же инволюцию ρ сопряженных прямых с двойными прямыми u, v. Справедливо и обратное утверждение: если какая-либо коника устанавливает в точке V инволюцию ρ, то эта коника обязательно касается двойных прямых u, v инволюции ρ.

24. Теперь можно четко сформулировать задачу построения коники, касающейся пары мнимых двойных прямых эллиптической инволюции V(h-h1, d-d1): искомая коника должна устанавливать в пучке V заданную инволюцию сопряженных прямых. Неопределенное и даже несколько романтическое условие соприкосновения с мнимыми прямыми заменено строгой геометрической формулировкой.

25. Конечно, в таком виде задача имеет множество (“бесконечность в третьей степени”) решений, потому что условие соприкосновения с двумя прямыми (действительными или мнимыми – безразлично) оставляет конике три степени свободы.

26. Чтобы конкретизировать задачу, надо указать пять инциденций. Например, пусть задана марка V(h-h1, d-d1) (две мнимые прямые), задан маркер x(O, L) (две мнимые точки) и дана действительная точка M (рис. 3, в). Получено лаконичное графическое изображение, позволяющее конструктивно построить главные оси коники, проходящей через точку M и устанавливающей на прямой x и в точке V заданные эллиптические инволюции. Задача имеет четыре решения. Алгоритм решения предложен А.Г. Гиршем, дополнен В.А. Коротким.

27. Таким образом, графическое представление мнимых элементов в виде маркеров и марок, предложенное А.Г. Гиршем, имеет ясный геометрический смысл и удобно в конструктивных построениях. Например, для поиска пары сопряженных точек в инволюции, заданной маркером x(O, L), надо всего лишь провести через L две взаимно перпендикулярные прямые, которые высекают на x искомые сопряженные точки.

Указатель сочетаний

28. Перечислим сочетания мнимых и действительных элементов (точек и касательных), определяющих кривую второго порядка. С учетом принципа двойственности, всякое сочетание имеет своего “двойника”, поэтому использована нумерация в виде дроби. Например, задачи 1/1 и 1/2 взаимно двойственны.

1/1. Пять точек, две из которых мнимые.

1/2. Пять касательных, две из которых мнимые.

2/1. Пять точек, четыре из которых мнимые.

2/2. Пять касательных, четыре из которых мнимые.

3/1. Три действительные точки, две мнимые касательные.

3/2. Три действительные касательные, две мнимые точки.

4/1. Одна действительная точка, четыре мнимые касательные.

4/2. Одна действительная касательная, четыре мнимые точки.

5/1. Одна действительная точка, две мнимые точки, две мнимые касательные.

5/2. Одна действительная касательная, две мнимые касательные, две мнимые точки.

6/1. Две действительные точки, одна действительная касательная, две мнимые точки.

6/2. Две действительные касательные, одна действительная точка, две мнимые касательные.

7/1. Одна действительная точка, две действительные касательные, две мнимые точки.

7/2. Одна действительная касательная, две действительные точки, две мнимые касательные.

В этот указатель не включены сочетания, когда на мнимой касательной указана мнимая точка прикосновения (см. п. 32).

Исторический обзор

29. Мнимые (комплексно сопряженные) элементы в алгебре трактуются как корни алгебраических уравнений. В курсе высшей геометрии учение о мнимом распространяется на геометрические образы [5].

30. Впервые в России тему мнимого в геометрии начал разрабатывать последователь Н.В. Лобачевского, профессор Казанского университета Федор Матвеевич Суворов (1845-1911). В работе [6], написанной в 1884 году, он систематически изложил конструктивные методы проективной геометрии, позволяющие выполнять построения с участием мнимых точек и мнимых прямых.

31. В этой работе даны примеры построения кривых второго порядка по данным воображаемым (мнимым) точкам и воображаемым (мнимым) касательным. Решены задачи 1/1, 2/1, 3/1 и коррелятивные (двойственные) им задачи 1/2 , 2/2, 3/2. Рассмотрена задача 4/1 и двойственная ей задача 4/2, но решение не завершено.

32. Также в работе [6, стр. 110] дан простой алгоритм построения коники для тех случаев (не вошедших в указатель сочетаний), когда на мнимой касательной дана мнимая точка прикосновения.

33. Задачи 5…7 в работе [6] не рассматривались.

34. Советский математик Овсей Аронович Вольберг в замечательном пособии для учителей средней школы [7] рассмотрел решение задач 1, 2 с использованием гармонической (инволюционной) гомологии, преобразующей искомую конику в себя. В этом же пособии (стр. 151) предложен проективный алгоритм построения коники, заданной действительной точкой, двумя мнимыми точками на прямой x и полюсом X прямой x относительно искомого конического сечения.

35. В.А. Пеклич в учебном пособии [8] предложил “начертательно-проективный” вариант построения коники, заданной мнимыми элементами. В построениях используются как проективные инварианты, так и способ выхода в пространство. Такой эклектический подход не является универсальным, но служит хорошим учебным упражнением, как в начертательной, так и в проективной геометрии. Решены задачи 1/1, 2/1, 3/1, 4/2, 6/1 (две последние задачи решены только для частного случая, когда данная касательная – несобственная).

36. Современное рассмотрение мнимых геометрических образов дано в работах А.Г. Гирша [3, 4]. Задачи 5…7 находятся в процессе решения. Задачи 4/1 (два решения) и 5/1 (четыре решения) решены полностью (совместно с В.А. Коротким).

Ошибка профессора Суворова

37. Ошибка (точнее говоря, незавершенное решение) допущена Ф.М. Суворовым при построении конического сечения, проходящего через действительную точку A и касающегося двух пар мнимых прямых, заданных на чертеже марками V1 и V2 (сочетание 4/1, рис. 4, а).

38. Следуя Ф.М. Суворову, находим мнимые точки пересечения двух пар мнимых касательных. Эти четыре мнимые точки попарно расположены на двух действительных прямых x, y, пересекающихся в точке Z. Пучки V1, V2 устанавливают на прямых x, y тождественно совпадающие инволюции.

39. Точку Z найти легко. Она определяется на пересечении прямых, которые в пучках V1, V2 соответствуют прямой z=V1-V2. Несколько сложнее найти прямые x, y. Конструктивное построение прямых x, y в работе [6] не рассматривается. Такое построение существует (рис. 4, б).

40. Далее в [6] доказывается утверждение, которое в современных терминах формулируется следующим образом. Если в пучках V1, V2 заданы инволюции ρ1, ρ2, то прямые x, y, на которых данные пучки устанавливают тождественные инволюции, являются сторонами автополярного треугольника, общего для всех коник, касательных к двойным прямым инволюций ρ1, ρ2. Третья сторона автополярного треугольника совпадает с прямой z.

41. Вершины X, Y, Z и стороны x, y, z найденного автополярного треугольника образуют три гармонические гомологии, в которых данной точке A соответствуют точки B, C, D. Искомое коническое сечение обязательно должно проходить через точки A, B, C, D.

42. Но коническое сечение определяется пятью точками, а не четырьмя. Как построить недостающую пятую точку искомой коники? Здесь Ф.М. Суворов допустил ошибку. Он предположил, что одна из найденных точек (например, точка B) может, в свою очередь, дать новые дополнительные точки искомой коники. Это неверно, потому что все три гомологии, образованные автополярным треугольником, инволюционны. В этих гомологиях точке B соответствуют точки A, C, D. Новых точек не возникает.

43. Таким образом, рассматриваемая задача в работе [6] до конца не доведена. Сохранилась проблема “пятой точки”.

44. Для решения этой пикантной проблемы подведем промежуточные итоги. Пучки V1, V2 порождают треугольник XYZ, который является автополярным для всех конических сечений, касающихся двойных прямых пучков V1, V2. Кроме того, известны четыре точки A, B, C, D искомой коники. Это хороший результат, но еще не решение.

45. Все конические сечения, проходящие через A, B, C, D, образуют пучок δ кривых второго порядка с общим автополярным треугольником XYZ. В пучке δ есть коника e (искомая), касающаяся мнимых двойных прямых инволюций  ρ1, ρ2.

46. Для выделения искомой коники e из пучка δ надо указать какое-нибудь дополнительное условие, которому она должна подчиняться. Например, можно взять пару сопряженных главных направлений h-h1 в пучке V1 и вспомнить, что полюс H прямой h относительно искомой коники обязан лежать на h1. Начертим гомалоид g прямой h в квадратичном кремоновом преобразовании, установленном пучком конических сечений δ(ABCD) [9]. Точки H1, H2 пересечения гомалоида с прямой h1 – два возможных полюса прямой h относительно искомой коники пучка δ (рис. 4, в).

47. Зная, что H1 и h – полюс и поляра относительно искомой коники, легко найдем пятую точку E1 и получим коническое сечение e1(A, B, C, D, E1). Это первое решение задачи. Аналогично, зная, что H2 и h – полюс и поляра относительно искомой коники, найдем пятую точку E2 и конику e2(A, B, C, D, E2). Это второе решение. Несложные вспомогательные действия, необходимые для конструктивного построения точек E1, E2, на рис. 4, г условно не показаны.

48. Кривую второго порядка g называют девятиточечным коническим сечением четырехугольника ABCD относительно прямой h. Оно содержит девять особых точек: вершины X, Y, Z автополярного треугольника,  общего для всех коник пучка δ, и еще по одной точке на каждой стороне полного четырехугольника ABCD [10].

49. Заметим, что для решения задачи нет необходимости вычерчивать непрерывный гомалоид g. Достаточно знать всего пять точек кривой g, чтобы найти (циркулем и линейкой) необходимые нам точки H1, H2 ее пересечения с прямой h. 

Заключение

В заключение хотелось бы повторить слова Ф.М. Суворова: “…построение кривых второго порядка, определяемых воображаемыми точками и воображаемыми касательными, …представляет столь же мало затруднений, как и построение по реальным точкам или касательным” [6]. Задачи 5…7 из указателя сочетаний, которые никем и никогда не рассматривались, обязательно будут в ближайшее время решены совместными усилиями А.Г. Гирша, В.А. Короткого и всех желающих принять участие в этом маленьком геометрическом приключении.

Список литературы

1. Короткий, В.А. Синтетические алгоритмы построения кривой второго порядка / В.А. Короткий // Вестник компьютерных и информационных технологий. – 2014. - №11. – С. 20-24.

2. Программа для ЭВМ «Построение кривой второго порядка, проходящей через данные точки и касающейся данных прямых» / В.А. Короткий // Свидетельство о государственной регистрации № 2011611961 от 04.03.2011 г.

3. Гирш, А.Г. Наглядная мнимая геометрия: монография / А.Г. Гирш. – М.: ООО ИПЦ «Маска», 2008. – 216 с.

4. Гирш, А.Г. Комплексная геометрия – евклидова и псевдоевклидова: монография / А.Г. Гирш. – М.: ООО ИПЦ «Маска», 2013. – 216 с.

5. Клейн, Ф. Высшая геометрия: монография / Ф. Клейн. – М.: УРСС, 2004. – 400 с.

6. Суворов, Ф.М. Об изображении воображаемых точек и воображаемых прямых на плоскости и о построении кривых линий второй степени, определяемых с помощью воображаемых точек и касательных. – Казань: Типография императорского Университета. – 1884. – 130 с.

7. Вольберг, О.А. Основные идеи проективной геометрии: учебное пособие / О.А. Вольберг. – М.-Л.: Учпедгиз, 1949. – 188 с.

8. Пеклич, В.А. Мнимая начертательная геометрия: учебное пособие / В.А. Пеклич. – М.: Изд-во АСВ, 2007. – 104 с.

9. Короткий, В.А. Квадратичное преобразование плоскости, установленное пучком конических сечений / В.А. Короткий // Омский научный вестник. – 2013. – № 1(117). – С. 9-14.

10. Кокстер, Х.С.М. Действительная проективная плоскость: монография / Х.С.М. Кокстер. – М.: Физматлит, 1959. – 280 с.

Рисунки к докладу

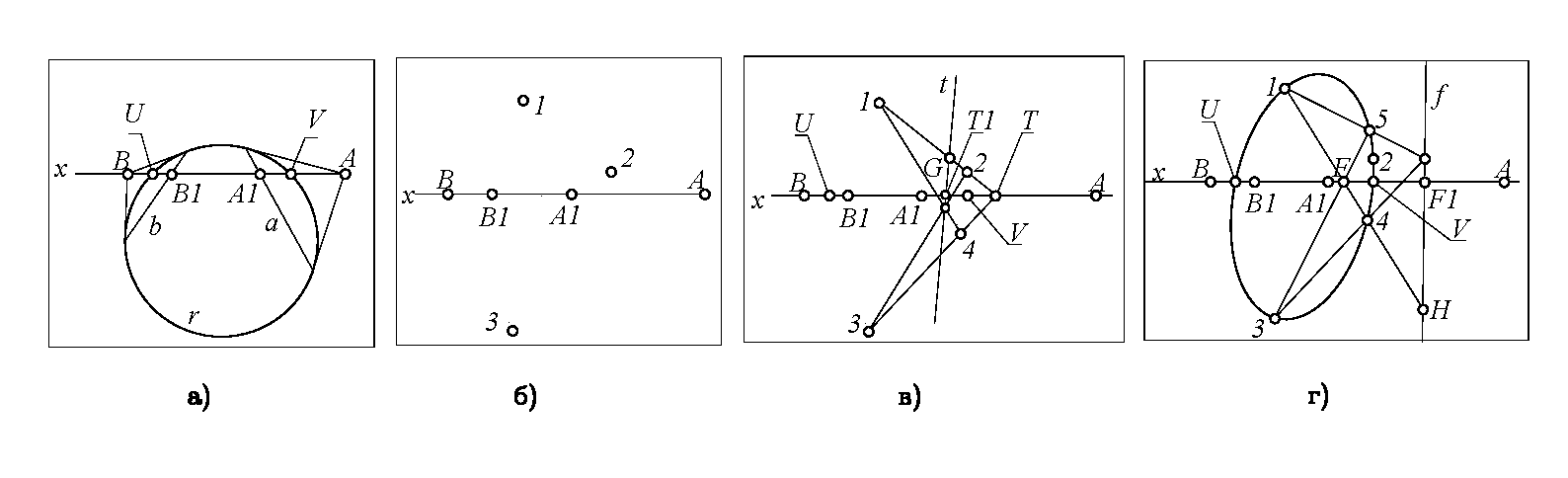
Построение коники, проходящей через точки 1, 2, 3 и через условно недоступные точки U, V пересечения окружности r с прямой x: а – инволюция на прямой x; б – исходные данные; в, г – построение дополнительных точек 4, 5 и решение задачи

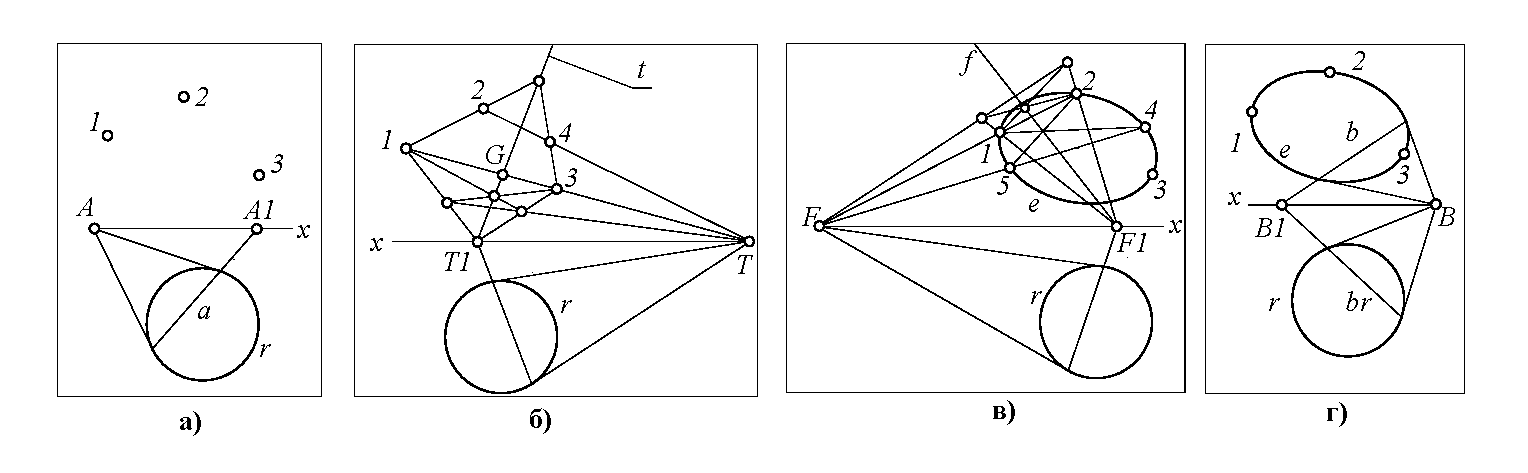
Построение коники e, проходящей через точки 1, 2, 3 и через мнимые точки пересечения окружности r с прямой x: а - исходные данные; б, в – построение дополнительных точек 4, 5; г – проверка решения

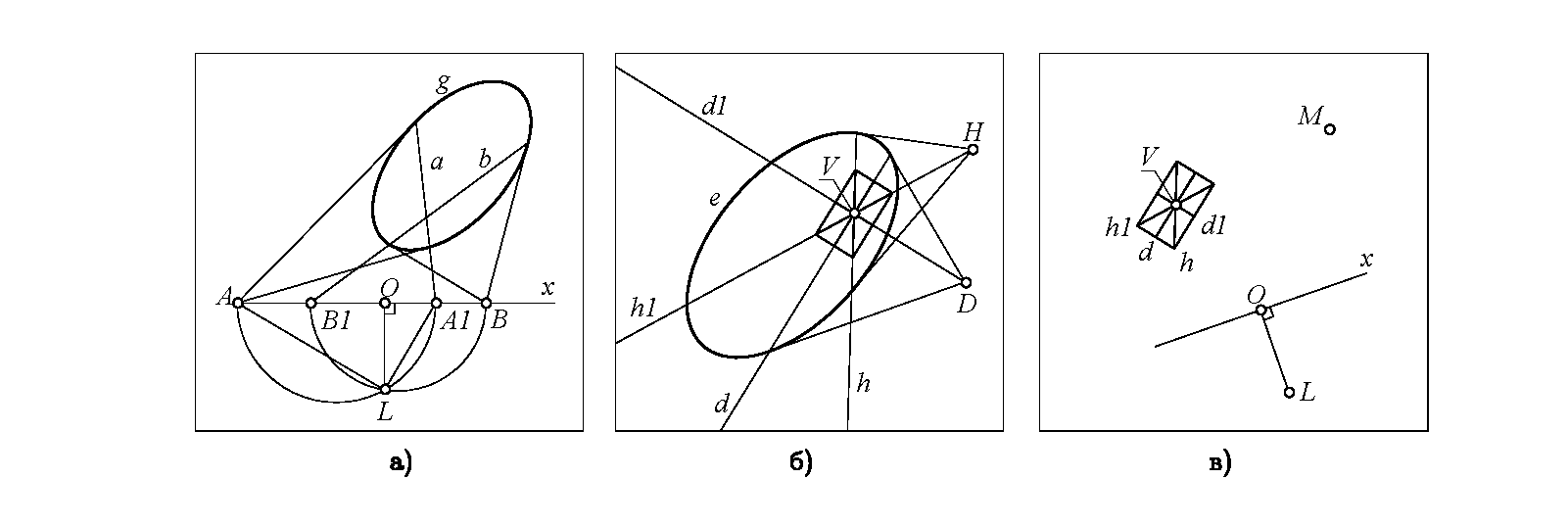
Изображение мнимых элементов: а – маркер x(O,L), б – марка V(h-h1, d-d1), в – коника задана парой мнимых точек x(O,L), парой мнимых касательных  V(h-h1, d-d1) и точкой M

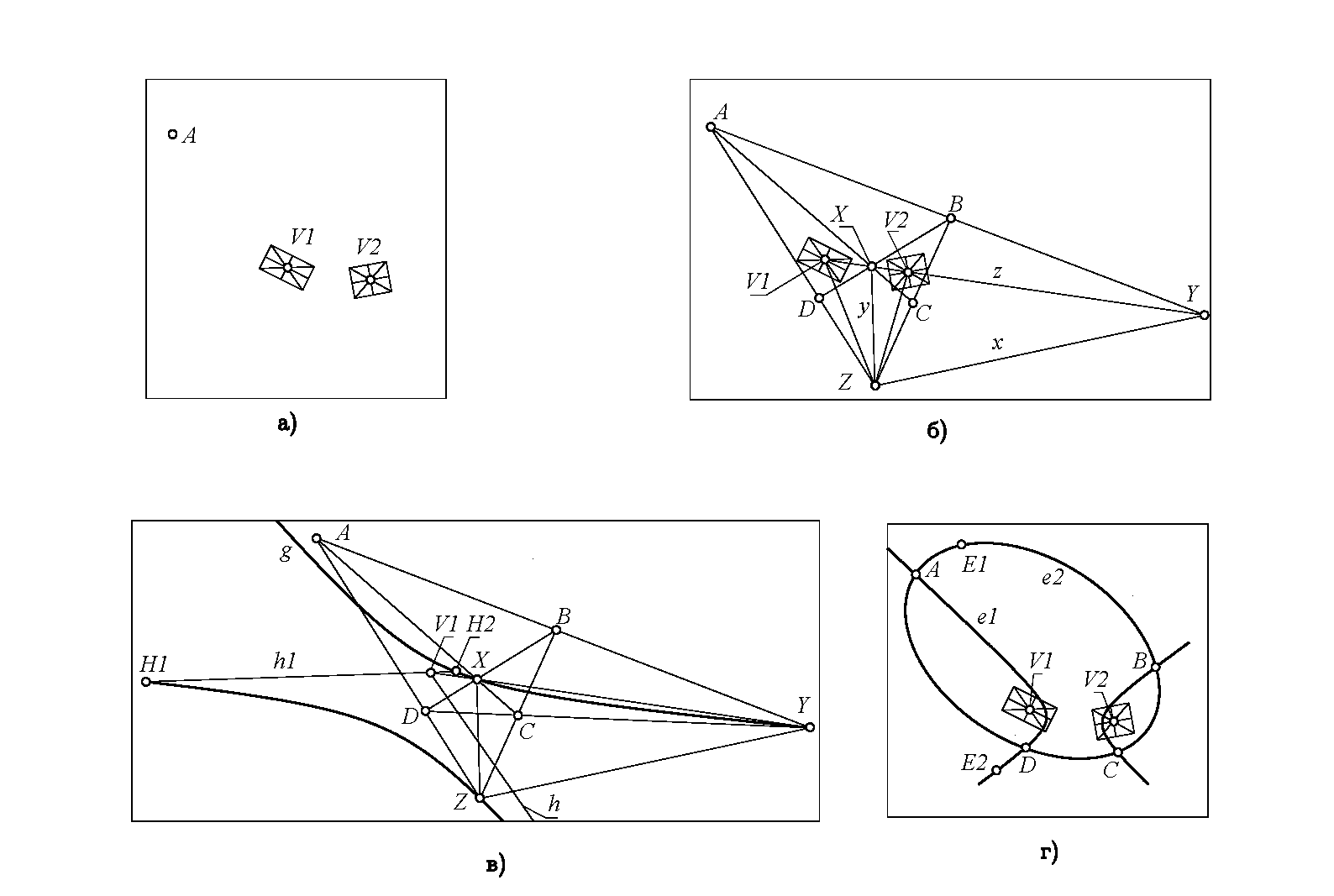
К задаче 4/1: а – исходные данные (точка A и две пары мнимых касательных), б – автополярный треугольник, в – гомалоид прямой h, г – два решения

Гирш Антон Георгиевич (10 марта 2016 г. 23:43)	Здравствуй, Виктор Анатольевич. С интересом прочитал доклад про мнимые элементы в алгебре и геометрии. Кроме чисто познавательного аспекта, приятно радует лёгкость и живость изложения такой, надо признаться, непростой темы. Именно такое изложение придаёт теме привлекательность. Но есть и но. В пункте 18 стоит вопрос "Кто их видел?" Во-первых, псевдоевклидовы фигуры (их чаще называют образы, чтобы не дай бог не попасть мимо) на евклидовой плоскости показать невозможно по определению. Во-вторых, если нельзя, но очень хочется, то можно, например, на чертеже совмещённых эпюров. По электронке пришлю картинки того, как получаются мнимые точки действительной коники и как выглядят мнимые касательные к действительной конике. По п.35 я бы не стал загромождать чертёж вспомогательной коникой, которая не имеет отношения к задаче и была краткосрочно придумана Пекличем, чтобы объяснить себе мнимые точки. По п.44 сделан отличный ход. Я сам попал в эту потенциальную яму, из которой показан выход. А с гомолоидом – это просто замечательно! Мастерский ход мысли. Молодец. С уважением. Антон Г.Гирш.
Короткий Виктор Анатольевич (11 марта 2016 г. 9:46)	Антон Георгиевич, у М. Жванецкого есть рассказ "Ставь птицу". Помните? Карцев и Ильченко. "Какие ребята, кто их видел?". В геометрии, как в литературе, есть место для всех жанров - и для  легких рассказиков наподобие - "Провести прямую через недоступную точку, которую никто не видел"и для монументальной классики: "Товарищи студенты! Давайте без шуток и в особенности без начертательной геометрии! Весь этот год моделируем троллейбус в 3D с выводом результата на 3D-принтер! Безбумажная технология!. К концу года будем уметь моделировать троллейбусы." Разве это плохо? Нет, это хорошо и полезно. В оркестре тоже есть разные инструменты. Есть слабенькие - гобой, фагот какой-нибудь, которые никто особо и не слышит. А есть сильные - барабан, литавры. Можно ли весь оркестр заменить барабаном? А можно ли всю геометрию заменить 3D- моделированием? Выкинуть из геометрического оркестра нач. геометрию? На Западе так и делают, и неплохо живут. Помните, Вы давали ссылку на современный германский учебник НГ выпуска 2015 года, объемом более 500 стр, для технических университетов? Ведь там нет ни одного чертежа. Только наглядные 3D картинки. Вот вам пожалуйста. Весь оркестр из одного барабана. И ничего. Как звучит! С уважением, В. Короткий
Панчук Константин Леонидович (11 марта 2016 г. 21:33)	Виктор Анатольевич, здравствуйте! Впечатляет  Ваша работа по кривым второго порядка. Системно и професионально! Что дальше по большому счету? Кривые более второго порядка на евклидовой плоскости, квадрики и более выокого порядка алгебраические поверхности в евклидовом пространстве? Видите ли Вы возможность практических приложений результатов системного завершения исследований кривых второго порядка? Начертательная геометрия хоть и маленький инструмент в "геометрическом оркестре", но она солидно питала, и хотелось бы чтобы всегда питала практику своими идеями и методами. Хотелось бы отметить работу  еще одного нашего соотечественника П.Флоренского "Мнимости в геометрии", в которой рассматривались и  практические мотивации мнимостей. С уважением, К.Л. Панчук.
Гирш Антон Георгиевич (12 марта 2016 г. 16:36)	Константин Леонидович, Виктор Анатольевич, вы хорошие специалисты и хорошо говорите о геометрии и практических приложениях. Гносеологический аспект – это тоже приложение. Алгоритмы перехода от комплексного задания коник к заданию действительными элементами – это добрый вклад в машинную графику как форма перекодирования, как своеобразный конвертор. За усилия и вклад Виктора Анатольевича в геометрию ценящие этот вклад коллеги должны были бы поднять его статус до доктора либо по совокупности трудов и изобретений, либо стимулировать его к написанию диссертации. Это был бы реальный вклад в начертательную геометрию. По другим специальностям такое практикуется, а начертальщиков всё жаба давит, однако. С уважением А.Г. Гирш.
Короткий Виктор Анатольевич (12 марта 2016 г. 18:22)	Антон Георгевич, Константин Леонидович! Кривые второго порядка играют совершенно исключительную роль в наших земных делах. Это базовые, фундаментальные кривые, которые появляются, причем иногда самым неожиданным образом, в самых разных задачах - математических, физических, технических. На сегодня имеется комплекс алгоритмов и программ, с помощью которых можно совершенно спокойно и безупречно точно ("циркулем и линейкой!") находить главные оси, асимптоты, фокусы, да еще и вычерчивать конику, инцидентную ЛЮБОМУ непротиворечивому набору 5 линейных элементов (точек, прямых), хоть действительных, хоть мнимых (некоторые наборы с мнимостями еще не алгоритмизированы). Таких наборов, считая двойственные, примерно 65. Этот программный комплекс - не более, чем чертежный инструмент. Нужен ли такой комплекс? Где? Кому? Не знаю. В прикладных пакетах компьютерной графики и САПР активно используются разнообразные составные кривые из кусочков кубических парабол, а кривые второго порядка на положении бедной родственницы. Не иначе, кривые второго порядка морально устарели и свою исключительную роль в нашем мироздании утратили. С уважением, Короткий В.А
Бойков Алексей Александрович (12 марта 2016 г. 20:03)	Виктор Анатольевич, здравствуйте! Рад новой встрече. Спасибо за доклад, как всегда, интересный и "геометричный". С уважением, Бойков
Гирш Антон Георгиевич (12 марта 2016 г. 21:11)	К посту от 12.03. Виктор Анатольевич, КВП, в бытность нормальной Украины, применялись для аэродинамических обводов и для конструирования зализов, т.е. переходных поверхностей. Кроме того, КВП, подобно точкам и прямым, служат элементами конструкций более сложных кривых, о чём и говорил Л.К. Панчук. Завдвинуть их на задворки никак не получится. С уважением. А.Г. Гирш.
Панчук Константин Леонидович (13 марта 2016 г. 17:09)	Согласен с мнением Антона Георгиевича о докторском статусе Виктора Анатольевича. В качестве первого шага необходимо структурировать накопленный материал (соотнести его с требованиями ВАК к докторским) и представить для рассмотрения на научном семинаре при диссертационном  совете у Сергея Игоревича. Предварительно эта тема обсуждалась на летнем совещании зав. кафедрами ГГП. Виктор Анатольевич! Активные действия в плане докторской должны быть с Вашей стороны. Мы можем лишь помогать. С уважением, К.Л. Панчук.
Ротков Сергей Игоревич (13 марта 2016 г. 18:34)	Виктор Анатольевич, Константин леонидович! О необходимости защиты докторской диссертации В.А.Коротким говорилось ему неоднократно. Последний раз в Дивноморском. Всегда будем рады заслушать его доклад на семинаре и высказать свое мнеение о проекте диссертационной  работы. С уважением, С.И.Ротков.
Гирш Антон Георгиевич (15 марта 2016 г. 1:44)	Уважаемые Сергей Игоревич, уважаемый Константин Леонидович, рад положительной реакции с вашей стороны на мой аппель. Виктор Анатольевич действительно граммотный и активный коллега, со здоровой гражданской позицией. Все мы только выиграем от его докторского статуса. С уважением вам  и пожеланием новых горизонтов Виктору Анатольевичу. Антон Г. Гирш.
Попов Евгений Владимирович (15 марта 2016 г. 19:05)	"В прикладных пакетах компьютерной графики и САПР активно используются разнообразные составные кривые из кусочков кубических парабол, а кривые второго порядка на положении бедной родственницы." Виктор Анатольевич, "составные кривые" в системах геометрического моделирования не только "кусочки кубических парабол", но и "кусочки парабол" более высоких порядков. Да, кстати, и более низкого 2-го порядка в том числе. Так что "бедной родственницей" она не является, это Вы зря.
Волошинов Денис Вячеславович (20 марта 2016 г. 15:49)	Присоединяюсь к мнению о том, что Виктор Анатольевич достоин ученого звания доктора наук. Интереснийший и богатейший материал, профессионализм - все налицо. Виктор Анатольевич, надо защищаться. Непростое это дело, но очень нужное! С уважением, Денис Волошинов
Короткий Виктор Анатольевич (20 марта 2016 г. 20:31)	"Машина,...считающая в миллион раз быстрее Вас, конечно, необычайно усиливает умственные способности и Ваши, и всего человечества. Это миф на все лады повторяется, внедряется, муссируется авторами научных трактатов. Здесь характерна ставка на технику. Техника ... усиливает его интеллектуальную мощь. Логика требует признать, что микроскоп и телескоп - это тоже усилители интеллектуальной мощи. И это, конечно, признается. Расширение опыта безнадежно смешивается или отождествляется с возможностями его истолкования, принятия, использования. Эффект молниеносного счета ....вызывает восхищение, а эффект МОЛНИЕНОСНОГО ПРОСЧЕТА тонет в стыдливом умолчании. Между тем, язык настойчиво ставит эти параллели: просчитать и просчитаться, способ и способности. Увеличение умственных способностей подразумевает, очевидно, гармоническое расширение ВСЕХ способов познания и учета всей данности, всей полноты. Поэтому уродливый горб ЭВМ, хлопотливо и молниеносно пересчитывающий жалкий скарб хронического недомыслия, останется как памятник одному из самых напыщенных и самых пустых мифов нашего века."  Кирилл Иванович Вальков, Язык и геометрия, 1981 г. Денис Вячеславович! У Вас был хороший учитель. Конечно, время идет. Ситуация меняется. Да, Вы правы: "уродливый горб ЭВМ" стал полноценным инструментом научного исследования. Как микроскоп, телескоп, осциллограф. Но не более того!!! Спасибо Вам за выступления на конференции. Вряд ли мы с вами дотянемся своим разумом до прекрасного русского христианского философа К.И. Валькова. Но мы будем учиться у него. С уважением, Виктор Короткий