В статье раскрывается инновационный подход в геометро-графической подготовке студентов горно-геологического профиля. Сущность подхода заключается в составлении комплекса специально подобранных инженерных задач, позволяющих осуществлять профессионально ориентированное обучение. Показано влияние данных задач на формирование геометро-графической компетентности студентов в их профессиональной сфере.
Ключевые слова: геометро-графическая подготовка; комплекс задач; инженерная задача; профессионально направленное обучение.
На целесообразность использования профессионально ориентированных задач как основного средства формирования у студентов соответствующих умений указывают многочисленные исследования в данной области (Аммосова М.С., Ахметханова Е.М., Васяк Л.В., Говоркова Л.И., Григоревская Л.П., Зубова Е.А., Петухова А.В., Скоробогатова Н.В., Федотова Т.И. и др.). Поскольку процесс решения задач является неотъемлемой частью геометро-графической подготовки, где задача как единица обучения играет ключевую роль, преподавание дисциплин графического цикла следует осуществлять с помощью специально подобранного комплекса задач. Между тем, создание такого комплекса (обоснованный подбор задач и выстраивание их в определенной последовательности) является одной из важнейших проблем, стоящих перед преподавателем. Это связано с тем, что в теории и практике обучения всегда возникает проблема определенной систематизации задач, их специального подбора, расположения в некоторой последовательности и формирования умений специфической деятельности решения.
Задачи, представленные в классических учебниках по геометро-графическому образованию и традиционно применяемые в учебной практике технических вузов, не могут в полной мере выполнить эту функцию, а главное – они зачастую не способны показать студентам реальную связь дисциплины с будущей профессией, то есть ее прикладную направленность, что негативно сказывается на мотивации обучения. Особенно это касается обучения студентов горно-геологического профиля, специфика будущей профессии которых значительно отличается от других.
В этой связи перед нами стола задача в рамках геометро-графической подготовки студентов горно-геологического профиля конкретизировать понятие «комплекс задач», установить наиболее общие принципы его формирования, удовлетворяющие определенному ряду требований и условий, и в соответствии с этим непосредственно разработать конкретные задачи.
Для уточнения понятия «комплекс задач» была выбрана исходная взаимообусловленная система, в которой выделен рассматриваемый объект. Под системой будем понимать множество элементов, находящихся в отношениях и связях друг с другом и образующих определённую целостность, единство. В качестве такой системы нами определена контекстная профессионально ориентированная образовательная среда геометро-графической подготовки (КПООС ГГП) [1]. В свою очередь комплекс, согласно словарю С.И. Ожегова, – это совокупность или сочетание чего-либо. Таким образом, комплексом задач, предназначенных для реализации геометро-графической подготовки студентов горно-геологического профиля, будем называть совокупность специально отобранных и структурированных в определенной последовательности задач, которые бы удовлетворяли образовательным целям курса дисциплин графического цикла, были направлены на формирование компетентностной модели выпускника соответствующего направления подготовки специалистов, мотивировали познавательную деятельность студентов, вызывали у них рефлексию и играли воспитательную роль.
В качестве основополагающих при решении данной проблемы были приняты следующие положения. Теоретическую основу при разработке комплекса задач составили следующие подходы: задачный, системный, компетентностный, контекстный, личностно-деятельностный, проектно-исследовательский, междисциплинарный, синергетический. В совокупности они позволяют преподавателю через задачи моделировать необходимые учебные ситуации и успешно реализовывать цели геометро-графического образования. При отборе содержания задач мы руководствовались принципами фундаментальности, сложности, открытости, интегративности и нелинейности.
Задания разрабатывались с учетом восприятия и понимания студентов первого курса. В этой связи базовые инженерные задачи [2] либо какие-то их составляющие, которые можно было рассматривать в рамках изучаемой дисциплины, преобразовывались и, соответственно, упрощались.
В результате был сконструирован комплекс задач, включающий задачи-упражнения (94 задачи) и 9 укрупненных задач, разработанных по вариантам – индивидуальные графические задачи (ИГЗ). Значительное место в комплексе занимают инженерные задачи, которые являются основой для решения практических задач разведки и разработки недр. Они содержат профессионально ориентированный контекст и подразумевают замещение реальных горно-геологических объектов их аналогами – геометро-графическими моделями. Для подготовки к решению таких задач была разработана тетрадь с печатными основами, содержащая задачи-упражнения [3]. Кроме того, изданы учебные пособия (рис. 1, а):
- «Начертательная геометрия в инженерных задачах» [4], где рассматриваются и технически обосновываются решения некоторых инженерных задач методами начертательной геометрии с алгоритмами решения и примерами оформления чертежей;
- «Теоретические основы построения геометрических объектов на планах» [5];
- «Метод проекций с числовыми отметками в решении инженерных задач» [6];
- «Экспресс-конспект» [7];
- «Начертательная геометрия применительно к решению горно-геологических задач. Геологическая структура с разрывным нарушением на горных чертежах» [8].
Для наглядности комплекс задач (КЗ) представлен в виде дерева задач (см. рис. 1, б). Все задачи комплекса вне зависимости от их сложности мы подразделяем на три группы. Первую группу составляют задачи классические (ЗК), традиционно представленные в учебниках по начертательной геометрии и инженерной графике. Во вторую группу включены профессионально ориентированные инженерные задачи (ЗИ), то есть проекции базовых инженерных задач, имеющих горно-геологическую специфику, решение которых может быть реализовано средствами начертательной геометрии, инженерной и компьютерной графики студентами первого года обучения в вузе соответствующих специальностей. Группа инженерных задач в свою очередь состоит из двух подгрупп 1 (ЗИ1) и 2 (ЗИ2). В первую подгруппу включены задачи, выбранные из первой группы классических задач, в содержание которых в результате их переформулирования введена горно-геологическая лексика, что придает задачам профессиональную направленность и дополнительно требует применения терминологического тезауруса. Вторую подгруппу представляют комплексные многокомпонентные инженерные задачи, базирующиеся на начальных геометро-графических знаниях и умениях, требующие пропедевтических знаний спецдисциплин и также использования профессионального терминологического тезауруса. К третьей группе задач отнесены задачи нестандартные (ЗН), такие как олимпиадные, творческие, исследовательские, задачи для работы в команде и др. Каждая из перечисленных задач может быть реализована на комплексном чертеже (КЧ), в проекциях с числовыми отметками (ПЧО), в аксонометрии (А), а также представлена в виде трехмерной модели (3D) в графических редакторах AutoCAD или KOMПАС. Таким образом, суммарно комплекс задач складывается из следующих составляющих:
КЗ = å ЗК(КЧ,ПЧО,А,3D) + å ЗИ1(КЧ,ПЧО,А,3D) + å ЗИ2(КЧ,ПЧО,А,3D) +å ЗН(КЧ,ПЧО,А,3D).
Далее каждую группу задач рассмотрим на примерах.
Задачи классические. Это задачи, которые в геометро-графической практике обучения решаются студентами всех технических вузов. В тетради с печатными основами классические задачи-упражнения занимают более 60 %. Они предназначены для решения на лекциях, практических занятиях и самостоятельной работы студентов. Отличительной особенностью данных заданий является то, что большинство из них предусматривает бинарный принцип решения, то есть студенты должны представить два или три обязательных решения: традиционное на комплексном чертеже, в аксонометрии и в проекциях с числовыми отметками. При этом алгоритм зачастую является единым для всех вариантов решения данной задачи, хотя могут быть применены и различные алгоритмы. Такой подход является новацией, поскольку в практике преподавания дисциплин графического цикла ранее не применялся.
Задачи инженерные. Задачи первой подгруппы (ЗИ1) инженерных задач также включены в тетрадь с печатными основами и аналогично задачам классическим предназначены как для решения в аудитории, так и самостоятельной работы и предусматривают одно, два или три решения. Вместе с тем в формулировке задач присутствует горно-геологическая лексика. Приведем пример такой задачи:
Через точку С запроектировать горную выработку CF, параллельную заданному направлению AB. Через точку D запроектировать горизонтальную горную выработку DE до пересечения с горной выработкой AB. Задачу решить в ПЧО (графически и аналитически), на эпюре и в прямоугольной изометрии.
Также к данной подгруппе отнесена, например, следующая индивидуальная графическая задача:
На эпюре (в двух проекциях) и в ПЧО определить расстояние между наклонными горными выработками а (АВ) и b (CD). Решение задачи на эпюре представлено в классических учебниках по начертательной геометрии. Пример выполнения задачи и алгоритм решения представлены на рис. 2, а.
Задачи второй подгруппы (ЗИ2) инженерных задач являются укрупненными комплексными инженерными задачами. Они играют обобщающую, интегративную, а также мотивирующую роль в процессе профессионально ориентированного освоения курса начертательной геометрии, инженерной и компьютерной графики, в формировании и закреплении навыков геометро-графического моделирования, осознанного выбора в каждом конкретной случае определенной геометро-графической модели объекта и наиболее рационального алгоритма решения задачи.
Пример задачи из подгруппы ЗИ2:
Вертикальные буровые скважины вскрыли в точках А, В, С и K, L, M крылья складки, поверхности которых могут быть представлены соответственно как плоскости S и L. Из данных бурения известны координаты точек А, В, С, K, L, M.
На эпюре (в двух проекциях) определить положение шарнира складки и величину угла складки m, а также натуральную величину плоскости крыла складки, ограниченную треугольником АВС и угол его наклона к горизонтальной плоскости проекций (метод выбрать самостоятельно). В ПЧО определить элементы залегания крыльев складки, величину угла складки m и элементы залегания осевой (биссекторной) плоскости Q.
Решение задачи на эпюре представлено в классических учебниках по начертательной геометрии. Пример выполнения данной задачи в ПЧО и алгоритм решения представлены на рис. 2, б.
Примеры выполнения других укрупненных комплексных задач из данной подгруппы приведены на рис. 3.
Здесь следует отметить, что в данной подгруппе задач в отличие от предыдущих (ЗИ2) уже не требуется выполнять несколько вариантов решения на различных геометро-графических моделях (комплексном чертеже, в проекциях с числовыми отметками или аксонометрии).
Решая данные задачи, студенты выбирают наиболее рациональную модель, выполняя конкретное действие в задании. Так, в некоторых индивидуальных комплексных инженерных задачах, необходимо решить ряд отдельных промежуточных задач на разных геометро-графических моделях в зависимости от того, на какой из них горно-геологический объект может быть представлен наиболее полно и рационально.
Выполняя данные задания, учащиеся овладевают навыками работы с горно-геологической документацией, что является чрезвычайно важным в формировании профессиональных компетенций будущих инженеров.
В отличие от традиционных классических задач (Зк), которые обычно заданы в виде знакомой геометро-графической модели и символики, отдельные инженерные задачи являются весьма сложными для самостоятельного решения студентами от начала до конца, что сопряжено с описательной (словесной) формулировкой задачи, а также нестандартными алгоритмами решения. В этом случае задача подразделяется на блоки: одни, безусловно, объясняются преподавателем, другие – студенты выполняют самостоятельно.
Необходимо подчеркнуть, что подавляющее большинство задач-упражнений служат подготовкой к выполнению индивидуальных графических заданий и являются аналогами их фрагментов, что значительно упрощает понимание сложных укрупненных задач.
Из третьей группы задач ЗН (задачи нестандартные), в настоящем исследовании нас интересуют только задачи, имеющие профессиональную направленность. Среди них можно выделить такие, которые студенты по завершении курса геометро-графической подготовки формулируют и решают самостоятельно, а затем разбирают их с преподавателем (индивидуальная работа). В эту же группу задач входят задания, которые сильные и особо мотивированные студенты по желанию выполняют самостоятельно сверх программы курса. Кроме того, задачи, входящие в комплекс, могут быть расширены специальными дополнительными заданиями. Например, задача, приведенная на рис. 2а, может рассматриваться как исследовательская задача [9], а одна из задач, представленных на рис. 3, как показал опыт, хорошо решаетя в команде. Также разработана методика решения этих задач. Все индивидуальные графические задания могут выполняться студентами вручную, а также в графических редакторах AutoCAD или КОМПАС в режиме 2D, причем одно не должно исключать другое, поскольку именно пара «голова-рука» активизирует процесс мышления. Кроме того, некоторые горно-геологические объекты для наглядности и лучшего понимания следует представлять 3D моделями. Особенно это полезно при построении блок-диаграмм месторождений и тектонических нарушений, а также наглядных изображений горных выработок.
Разработанный комплекс задач способствует активному формированию дисциплинарных компетенций и соответствует синергетическим принципам: фундаментальности, сложности, открытости, нелинейности. Принцип фундаментальности согласуется с тем, что позволяет выявить в изучаемой дисциплине знания для профессионального использования. Принцип сложности проявляется в следующем: все индивидуальные графические задания (ИГЗИ2) являются сложными, но вместе с тем доступными для понимания студентами первого курса. Кроме того, при необходимости задания могут быть дополнены или упрощены. Это не влечет принципиальную потерю их качества и позволяет реагировать на индивидуальность, как отдельного учащегося, так и группы учеников. В соответствии с принципом открытости можно варьировать задачи в зависимости от направления подготовки учащихся, также имеется возможность применять в образовательном процессе различные методики и новации. Комплекс задач учитывает принцип нелинейности, поскольку предполагает возвращение к определенным темам на разных уровнях и различные методы решения одних и тех же задач, в результате чего у студентов формируется целостная система знания.
Присутствие в образовательном процессе инженерных задач ускоряет и качественно изменяет само обучение за счет появления дополнительной мотивации, поскольку студентам видна очевидная связь дисциплины с будущей профессиональной деятельностью. Кроме того, решение инженерных задач оказывает положительный эффект и на усвоение задач классических, усиливая их роль как в формировании геометро-графической компетентности, так и в формировании компетентностной модели выпускника вуза конкретного направления подготовки.
В этой связи инженерные задачи, вошедшие в разработанный комплекс задач, удовлетворяют следующим условиям:
- описывают объекты или ситуации из горно-геологической инженерной деятельности;
- содержат некоторые неизвестные параметры горно-геологических объектов или явлений, которые необходимо определить или исследовать с помощью аппарата начертательной геометрии инженерной и компьютерной графики;
- способствуют прочному усвоению геометро-графических знаний, являющихся основой инженерной деятельности любого профиля и формированию геометро-графической компетентности;
- обеспечивают установление взаимосвязей дисциплин графического цикла со специальными дисциплинами;
- устанавливает пропедевтическую стадию изучения понятий спецдисциплин и терминологического тезауруса;
- направлены на формирование профессиональной компетентности (не только по-возможности большего количества ее квалификационных составляющих, но и более высокий уровень их сформированности);
- оказывают воспитательное действие на учащихся, что реализуется через такие многочисленные аспекты как прикладная и мировоззренческая направленность, воспитание интереса, развитие творческих задатков и нравственных качеств личности и т.д.
Функции инженерных задач представлены на рис. 4.
Разработанный комплекс инженерных задач, включающих профессионально ориентированный контекст соответствует пониманию и восприятию студентов первого курса, делает обучение профессионально направленным и при этом усиливает позиции классического обучения, способствует формированию способности и готовности применять полученные знания как в спецдисциплинах, так и в будущей профессиональной деятельности.
Принцип бинарности при решении задач, когда решение одной и той же задачи осуществляется параллельно на разных геометро-графических моделях с использованием единого или различных алгоритмов, благотворно отражается на понимании и усвоении учебного материала, дает опыт по выбору оптимального решения.
P.S. Уважаемые коллеги!
Описанный в статье комплекс задач разрабатывался и внедрялся на протяжении 20 лет. Результаты внедрения созданной методики положительные, о чем многократно докладывалось на различных конференциях как в нашей стране, так и за рубежом, имеется 5 публикаций в ВАК журналах.
Однако в настоящий момент в связи с унификацией программ геометро-графическая подготовка студентов горно-геологического профиля в нашем вузе осуществляется наравне со студентами всех других специальностей.
Если для кого-то актуальны методические разработки в данном направлении, охотно поделюсь (е-mail: alamanta@mail.ru ).
Список литературы
1. Контекстная профессионально ориентированная образовательная среда как средство // . 2012. № 6. С. 27-37.
2. Верещагина Т.А. Эволюционный процесс формирования умений решения инженерных задач // Инновации в образовании. 2013. № 10. С. 27-35.
3. Боброва Л.Г., Верещагина Т.А., Начертательная геометрия: задачи с печатными основами: прил. к учеб. пособию «Начертательная геометрия: экспресс-конспект: Ч. 1» (задачник). Пермь: Изд-во Перм. гос. техн. ун-та, 2010. – 55 с.
4. Боброва Л.Г. Начертательная геометрия в инженерных задачах /Л.Г. Боброва, Т.А. Верещагина, В.В. Микова. – Перм. гос. техн. ун-т. – Пермь, 2010. – 49 с.
5. Боброва Л.Г., Верещагина Т.А., В. В. Микова. Теоретические основы построения геометрических объектов на планах: Учебное пособие/– Пермь, Перм. гос. техн. ун-т, 2006. – 35с.
6. Верещагина Т.А., Кочурова Л.В., Турицына И.А. Метод проекций с числовыми отметками в решении инженерных задач. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2016. – 105 с.
7. Боброва Л.Г., Верещагина Т.А. Начертательная геометрия. Часть I. Экспресс-конспект: Учебное пособие/– Пермь, Перм. гос. техн. ун-т, 2010. –55с.
8. Верещагина Т.А. Начертательная геометрия применительно к решению горно-геологических задач. Геологическая структура с разрывным нарушением на горных чертежах (методическое пособие). Перм. гос. техн. ун-т. – Пермь, 2000. – 24 с.
9. Верещагина Т.А. Исследовательская деятельность в геометро-графической подготовке // Теория и практика общественного развития. 2014. № 1. С. 226–229.
Рисунки к докладу
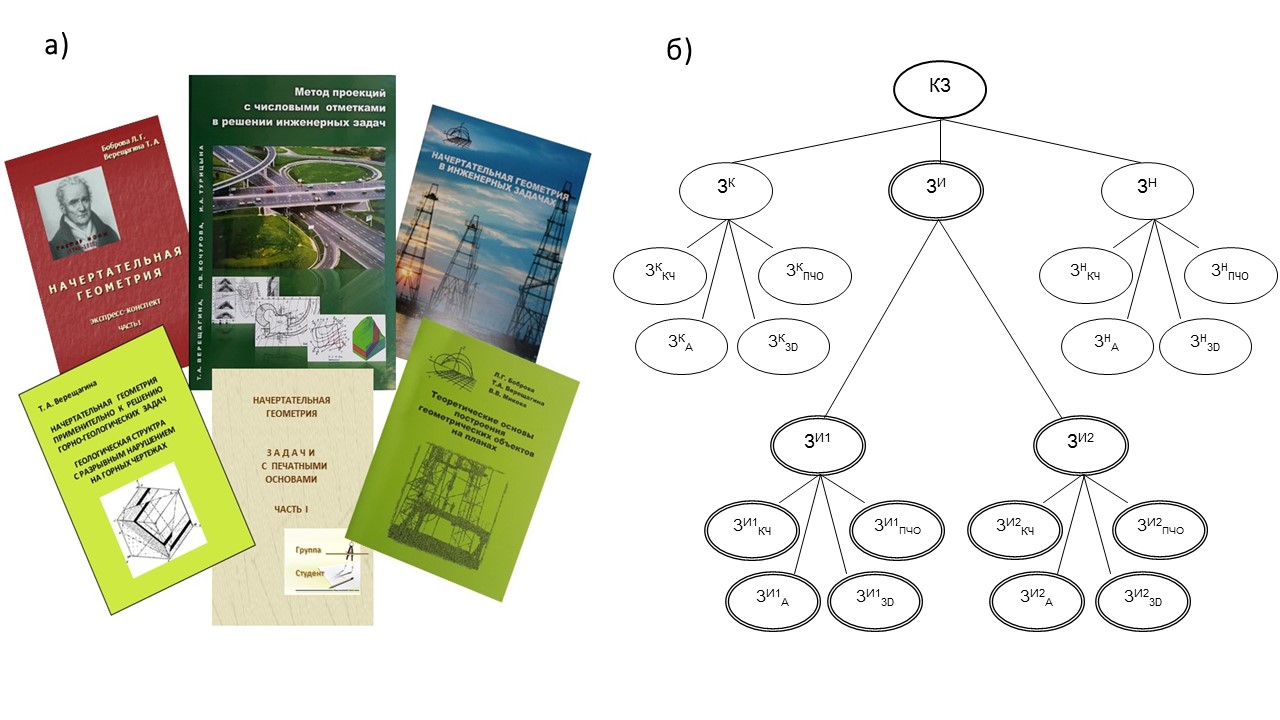
Рис. 1
Методическое обоснование для комплекса инженерных учебных задач: а) учебно-методическая литература; б) комплекс учебных задач, представленный в виде дерева задач
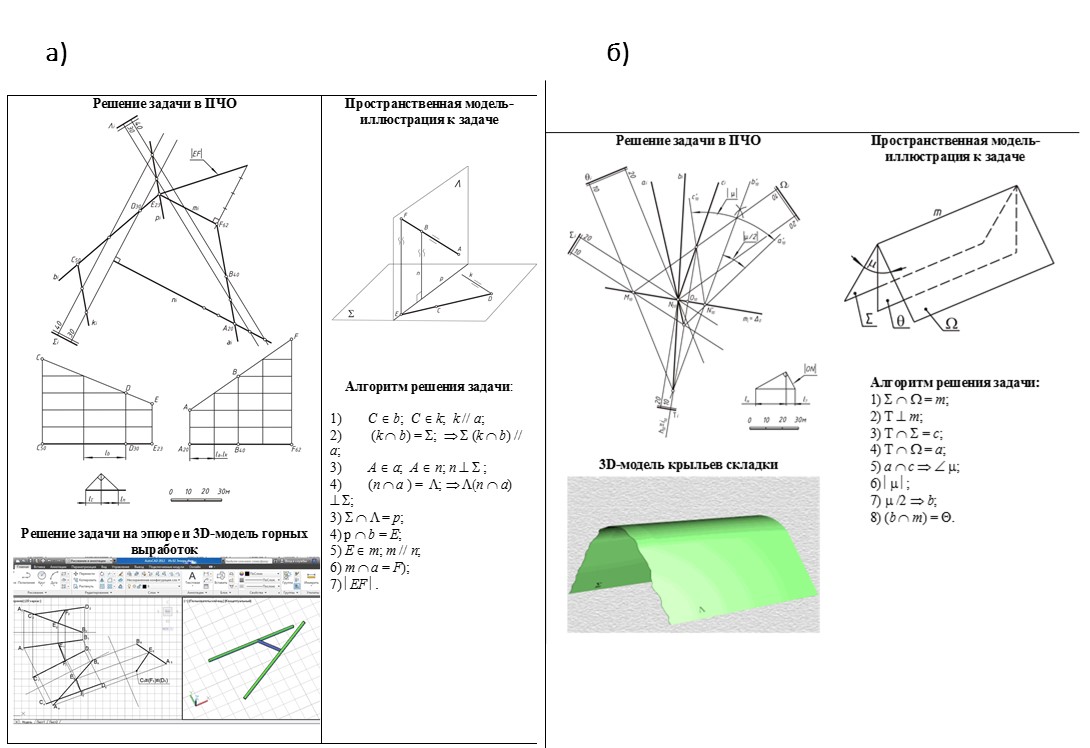
Рис. 2
Примеры выполнения инженерных задач: а) ЗИ1; б) ЗИ2
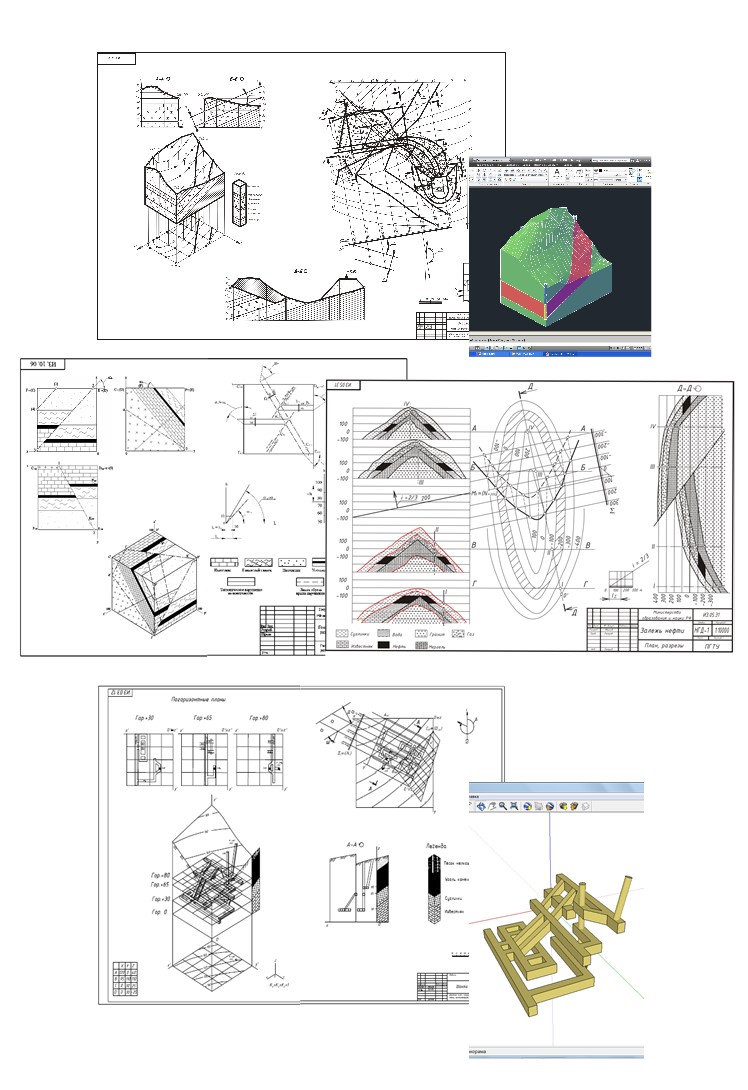
Рис. 3
Примеры выполнения укрупненных инженерных задач (подгруппа ЗИ2)
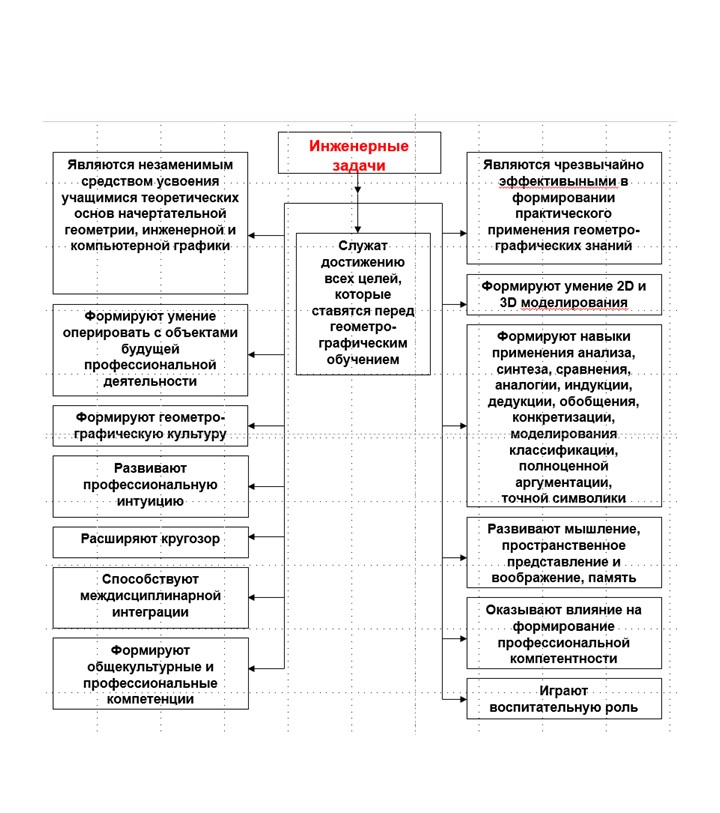
Рис. 4
Функции инженерных задач в геометро-графической подготовке
Вопросы и комментарии к выступлению:

Лепаров Михаил Николаевич (22 марта 2017 г. 2:37) |
Здравствуйте, уважаемая Татьяна Анатольевна!Примите мои поздравления за подхода- комплекс задач, у каждого из которых прямая связь с деятельностю будущего инженера. Идея замечательная. Жаль, очень жаль, что у Вас проблемы с дальнейшего применения. Мы с Александр Олегович Горнов тоже пропагандируем методологию с опорой на инженерные задачи и с удовольствием отмечаем, что мы с Вами единомышленники.Разрешите два вопроса:1. Какой примерный процент студентов, которые решают задачи из третьей группы (задачи нестандартные)?2. Все ли из этих студентов решают задачи до конца или некоторые бросают их по пути?Желаю Вам чудо (и идеи прежде того) для продолжение Вашу прежную деятельность. Пожалуйста, извините мой русский. С уважением млепаров |
|
Верещагина Татьяна Анатольевна (24 марта 2017 г. 0:43) |
Уважаемый Михаил Николаевич! Большое спасибо за интерес к моей работе и добрые комментарии. Приятно, что Вы и Александр Олегович также, как и я, считаете важным введение инженерных задач в учебный процесс. Когда-то от одного из студентов на первом занятии по начертательной геометрии я услышала: «А мой папа сказал, что начертательная геометрия никогда не пригодится»… Видимо, такое впечатление у папы сложилось потому, что он изучал нашу дисциплину как некую абстрактную науку, существующую «саму по себе», без ориентации на будущую специальность. Думаю, что именно инженерные задачи, введенные в геометро-графическую подготовку, способны показать каждому студенту важность изучения предмета и интеграцию его как со спецдисциплинами, так и с будущей профессией. Поэтому мы, преподаватели, должны помнить об этом. Отвечая на Ваши вопросы, хочу сказать, что на протяжении 20 лет детально разработаны и опробованы именно инженерные задачи, т.е. задачи из второй группы комплекса. Задачи из третьей группы (нестандартные задачи) я только начала вводить в учебный процесс, но довести эксперимент до конца мне, к сожалению, не разрешили. О том, что было сделано, скажу следующее. Нестандартные задачи решали только сильные студенты (остальные не успевали). Может это и правильно – у каждого своя траектория обучения, и сильных студентов надо выводить на более высокий уровень. Задачи совместными усилиями мы доводили до некоторого логического конца. Иногда круг рассматриваемых вопросов расширялся, а иногда было и наоборот. Студент по собственному желанию из любой спецлитературы по специальности «вытаскивал» какую-либо тему, связанную с чертежами, и выбирал там какой-нибудь кусочек для проработки. Роль преподавателя заключалась в том, чтобы помочь учащемуся «увидеть» задачу, сформулировать ее, проследить связи профессионального контента с нашей дисциплиной и задать вектор решения. При этом в проблему «погружались» как студент, так и преподаватель. И это была действительно творческая, обоюдно интересная работа. Конечно очень жаль, что на кафедре возврата к этому однозначно не будет. Еще хочу добавить, что я участвовала во всероссийском проекте на интернет-платформе института им. А.С. Пушкина (г. Москва) в создании бесплатного онлайн курса: Вводный курс «Применение основ начертательной геометрии, инженерной и компьютерной графики в решении инженерных задач» из цикла «Основы инженерного дела», где также сделан упор на обучение через инженерные задачи. Всего Вам доброго. С уважением, Верещагина Т.А. |

Лепаров Михаил Николаевич (24 марта 2017 г. 1:00) |
Здравствуйте, уважаемая Татьяна Анатольевна!Спасибо большое за ответы. „Роль преподавателя заключалась в том, чтобы помочь учащемуся «увидеть» задачу, сформулировать ее, проследить связи профессионального контента с нашей дисциплиной и задать вектор решения. При этом в проблему «погружались» как студент, так и преподаватель. И это была действительно творческая, обоюдно интересная работа.” На этом искренно завидую Вам. Пожалуйста, извините мой русский. С уважением млепаров |
Назад Go Back