

|
Короткий Виктор Анатольевич | (Южно-уральский государственный университет (Национальный Исследовательский Университет)) |
Рассмотрено комплексное учебное задание по инженерной компьютерной графике, включающее в себя как геометрические построения, так и алгебраические расчеты. Дан пример выполнения задания.
Требуется построить кривую с гладкостью не менее второго порядка, имеющую в заданных точках A и B данные касательные TA, TB и круги кривизны RA, RB (рис. 1). Найти уравнение кривой. Иначе говоря, надо спроектировать составляющую обвода не менее второго порядка гладкости, имеющую в заданных стыковых точках A, B данные касательные и круги кривизны [1].
Поставленную задачу можно решить разными способами. Например, в [2] была получена кривая, составленная из дуг кубических парабол с осями, параллельными координатным осям x, y. Это кубический сплайн второго порядка гладкости. Полученный сплайн выглядит как гоночная трасса, а не как технический обвод (рис. 1, а). Это хорошая трасса. Гонщик на такой трассе будет уверенно перекладывать свой мотоцикл из поворота в поворот, не испытывая “бокового сноса” (скачкообразного изменения центростремительной силы) в стыковых точках. Но для технических задач такой обвод не годится.
Кубический сплайн может быть отредактирован указанием дополнительных управляющих точек, хотя при этом стремительно растет число отсеков обвода. Теряется аналитическое описание. В результате обвод фиксируется не формулой, а дискретным цифровым массивом координат. К тому же график изменения кривизны по длине обвода – не гладкая, а ломаная кривая. Такое решение может оказаться технически неприемлемым.
Можно использовать параболы высокого порядка с риском получить непрогнозируемые осцилляции. Тоже плохо.
Есть удобный способ: надо взять подходящую САПР. Например, IndorCAD/Road. Изучим инструкцию к программе, разберемся с кнопками, зададим исходные данные, получим искомую кривую. Но, во-первых, эта кривая будет составной. Во-вторых, у нас все-таки учебный процесс, а не курсы пользователей специализированных САПР.
Мы рассмотрим алгоритм решения, основанный на обычной инверсии относительно окружности, но со смещенным центром преобразования. Забегая вперед, покажем результат: вместо составной кривой будет получена дуга c4 одной алгебраической нерациональной кривой четвертого порядка, удовлетворяющая поставленным граничным условиям (рис. 1, б). Алгоритм построения полностью, без каких-либо изменений, взят из работы [1, стр. 89].
Все знают, что такое инверсия. Это простейшая квадратичная инволюция. На совмещенной плоскости П=П′ чертят окружность d2. Берут произвольную точку M плоскости П. Ставят ей в соответствие такую точку M′ плоскости П′, что точки Q, P, M, M′, лежащие на OM, образуют гармоническую четверку (рис. 2, а). Окружность d2 называют инвариантной коникой, поскольку точки, инцидентные d2, при инверсии переходят в себя. Центр окружности O – центр преобразования. Любая прямая m (кроме слабоинвариантных прямых, проходящих через центр окружности) переходит в окружность m2, проходящую через центр O. Все окружности проходят через циклические точки I, J, следовательно, образ (гомалоид) любой прямой проходит через точки O, I, J, которые называют фундаментальными (в рассматриваемом случае – попарно совпавшими) точками плоскостей П=П′ (F-точками). Точки F1=F′1 совпадают с O, точки F2=F′3 и F3=F′2 совпадают с циклическими точками. Преобразование инволюционно, поскольку точке N=M′ отвечает точка N′=M. В качестве практических приложений инверсии в геометрии обычно называют построение профилей Жуковского. В школьной геометрии используют инверсию (совместно с преобразованием расширения) для решения задачи Аполлония.
Произвольным образом сместим центр O преобразования относительно центра окружности (рис. 2, б). Алгоритм построения соответственных точек остается прежним: (QPMM′)=-1. Получаем преобразование, которое называют обобщенной инверсией, или преобразованием Гирста [1]. Мнимые точки F2=F′3 и F3=F′2 покидают свои насиженные места I, J, хотя и остаются на окружности d2, указывая мнимые точки касания мнимых прямых, проведенных из точки O касательно к d2. Произвольная прямая m переходит в конику m2, инцидентную точке O=F1=F′1 и мнимым точкам F2=F′3, F3=F′2.
Примечание
Обобщенная инверсия (преобразование Гирста) может иметь в качестве инвариантной коники не только окружность, но и любую КВП, в том числе вырожденную КВП, распавшуюся на две прямые.
Вынесем центр преобразования O за пределы инвариантной окружности d2. Точки F2=F′3, F3=F′2, оставаясь на окружности d2, становятся вещественными. Образ m2 произвольной прямой m проходит через центр O и через точки F2, F3 (рис. 2, в).
Если центр O инцидентен инвариантной окружности, то F-точки совпадают с центром O: O=F1=F′1=F2=F′2=F3=F′3, вследствие чего образы всех прямых получают в O трехточечное соприкосновение друг с другом, в том числе и с образом p2 несобственной прямой (рис. 2, г). Образ несобственной прямой p2 называют предельной окружностью. Она проходит через центр инвариантной окружности d2.
Пока не очень понятно, как эти “наукообразные” рассуждения об инверсии с плавающим центром могут помочь при решении конкретной практической задачи. Зачем, например, рассматривать такой экзотический частный случай, когда центр O преобразования инцидентен инвариантной окружности, и все F-точки совпадают с точкой O? Для “наукообразия”? Конечно, нет. Именно этот частный случай позволяет эффективно решить задачу динамического сопряжения двух окружностей. Но предварительно следует рассмотреть вспомогательную задачу.
Обобщенная инверсия задана центром F1 и инвариантной окружностью d2. Требуется построить образ r окружности r0 (рис. 3). Отмечаем точки пересечения 1, 1′ окружности r с прямой j1=F2F3. Все точки этой прямой, в том числе и отмеченные точки 1, 1′, преобразуются в точку F1. Следовательно, F1 – двойная точка кривой r. Точки F2, F3 также двойные. Получаем образ окружности r0 – уникурсальную кривую r четвертого порядка (см. рис. 3). Очевидно, кривая r проходит через точки R, R′ пересечения инвариантной коники d2 с прообразом r0. Вспомогательная задача решена.
Если бы прообраз r0 не пересекался с прямыми j1, j2, j3, то образ r не прошел бы через точки F1, F2, F3. И наоборот – если прообраз пересекается с ji, то образ обязательно инцидентен точке Fi. Именно ради иллюстрации этого утверждения была рассмотрена вспомогательная задача. Еще раз подчеркнем – сколько раз прообраз пересекает исключенную прямую ji, столько раз образ проходит через ассоциированную с прямой ji точку Fi.
В частности, если все три F-точки совпадают с центром преобразования O (см. рис. 2, г), то исключенные прямые j1, j2, j3 совпадают между собой, занимая положение касательной t к окружности d2 в точке O. Если при этом окружность r0 пересекает касательную t (в двух точках), то ее образ r дважды пройдет через все три совпавшие F-точки. При этом обе ветви кривой r будут иметь в точке O круг кривизны, совпадающий с предельной окружностью p2 (см. рис. 2, г). Действительно, обе ветви кривой r и окружность p2 проходят через три совпавшие точки F1=F2=F3, следовательно, находятся в трехточечном соприкосновении.
Таким образом, в обобщенной инверсии с центром O, лежащим на d2, образ r окружности r0, пересекающей касательную t, имеет в точке O круг кривизны p2.
Напомним задачу. Даны окружности ρA и ρB (рис. 4, а). Требуется построить динамическое сопряжение данных окружностей, то есть такое сопряжение, при котором вторая производная плавно (без изломов) меняется вдоль искомой сопрягающей кривой.
Эта задача решена в [1]. Нам не надо ничего изобретать. Алгоритм, основанный на использовании свойств кремоновых преобразований плоскости с совпавшими F-точками, прописан с аптекарской точностью и полностью готов к употреблению. Задачу вполне возможно адаптировать к студенческому уровню, хотя в целом монография [1] написана безо всякого снисхождения к малограмотному читателю.
Действие первое. Одну из заданных граничных точек, например, точку B, принимаем за центр квадратичной инволюции I2 с совпавшими F-точками: B=F1=F2=F3. Заданный круг кривизны ρB считаем предельной окружностью p2 преобразования I2. Напомним, что p2 – образ (гомалоид) несобственной прямой, что позволяет однозначно начертить инвариантную окружность d2 (см. рис. 4, а). Таким образом, аппарат преобразования полностью определен. Какую пользу нам принесет это преобразование – пока неизвестно.
Действие второе. В инволюции I2 находим образ ρ′A круга кривизны ρA, заданного в условии задачи. Получаем алгебраическую кривую четвертого порядка ρ′A, форма которой приблизительно становится понятной после построения двух десятков точек этой кривой (см. рис. 4, а). Но этого недостаточно. Нам потребуется совершенно точно знать касательную и круг кривизны кривой ρ′A в точке A′ (здесь A′ - образ точки A в преобразовании I2).
Конечно, можно постараться получить эту информацию методами графического дифференцирования. Но результат будет плохой, несмотря на высокую точность компьютерных построений. Поэтому будем искать аналитическое решение.
Введем в рассмотрение систему координат xy, совместив начало координат с центром преобразования и направив ось y вдоль касательной t к инвариантной окружности d2 (см. рис. 4, а). В выбранной системе координат рассматриваемое преобразование I2 описывается уравнениями
x′=Rx2/(x2+y2-Rx), y′=Rxy/(x2+y2-Rx), (1)
где R=2RB – радиус инвариантной окружности d2 [1]. Преобразование инволюционно, поэтому формулы обратного преобразования получаются простой перестановкой координат x и x′, y и y′:
x=Rx′2/(x′2+y′2-Rx′), y=Rx′y′/(x′2+y′2-Rx′). (2)
Запишем уравнение круга кривизны ρA в выбранной системе координат:
(x-x0)2+(y-y0)2=R2A, (3)
где x0, y0, RA – координаты центра и радиус. Подставляя в (3) выражения (2) и опуская знак “штрих”, получаем уравнение кривой ρ′A:
F(x, y)=x4+Kx2y2+Dy4+F(x3y+xy3)+Tx3+Mx2y+Nxy2+Lx2=0. (4)
Это и есть уравнение образа ρ′A круга кривизны ρA в инволюции I2(B, d2). Для расчета численных значений коэффициентов уравнения (4) достаточно знать радиусы RA и RB окружностей кривизны ρA, ρB и координаты x0, y0 центра окружности ρA в выбранной системе координат (см. рис. 4, а).
Действие третье. По формулам (1) находим численные значения координат (x′, y′) точки A′, являющейся образом точки A в инволюции I2(B, d2). Вычисляем первую производную и радиус круга кривизны c′ кривой ρ′A в точке A′.
Сказать легко, сделать трудно. Надо продифференцировать неявно заданную функцию (4), то есть рассчитать первые и вторые частные производные. Это трудно. Но глаза страшатся, а руки делают. Через полчаса мы имеем аналитические выражения для производных. Например, вторая смешанная производная имеет вид:
F′′xy=4Kxy+3F(x2+y2)+2Mx+2Ny.
Еще через час найдем численные значения первой производной f′(x)=F′x/F′y=-1,10085 кривой ρ′A в точке A′ и радиус кривизны R′A=46,76342 в этой точке.
Зачем такая трудоемкая вычислительная работа в учебном процессе? Ответ простой. Инженер должен уметь доводить работу “до числа”. Для этого нужна тренировка, нужны соответствующие учебные задания. Да, это трудно. А кто сказал, что учиться легко? Не надо брать пример с западных вузов. Они проходят тему “вращательное движение” по учебному видеофильму “Велосипедист едет мимо Эйфелевой башни”, а на занятии “кривые линии” внимательно изучают фотографию цветка.
Действие четвертое. Зачем мы искали кривую ρ′A? Зачем определяли касательную и круг кривизны c′ этой кривой в точке A′? Это была трудная работа. Будет ли “награда”? Конечно. Для окончательного решения задачи надо всего лишь найти прообраз окружности c′ в обобщенной инверсии I2(B, d2). Этот прообраз – алгебраическая кривая четвертого порядка c4 с двойной точкой B (рис. 4, б).
Покажем, что кривая c4 удовлетворяет заданным граничным условиям. Действительно, обе ветви кривой c4 имеют в точке B один и тот же круг кривизны ρB=p2 (см. вспомогательную задачу). Граничные условия в точке B выполнены. Осталось показать, что кривая c4 удовлетворяет граничным условиям в точке A. Действительно, точка A′, лежащая на c′, в инверсии I2(B, d2) инволюционно возвращается на свое законное место – в точку A. Следовательно, прообраз c4 окружности c′ проходит через A. Окружность c′ имеет в точке A′ трехточечное соприкосновение с кривой ρ′A – образом круга кривизны ρA. Поэтому прообразы c4 и ρA обязательно будут иметь в точке A трехточечное соприкосновение, так как обобщенная инверсия, как и любое взаимно однозначное преобразование, сохраняет инцидентность [1].
Таким образом, алгебраическая кривая 4 порядка c4 содержит две разные дуги AB. Если не принимать во внимание направленность заданной касательной TA, то обе дуги удовлетворяют граничным условиям. С учетом направления TA следует выбрать “верхнюю” ветвь кривой c4 (см. рис. 4, б). Для получения уравнения кривой c4 надо в уравнение окружности c′ подставить выражения для x′, y′ из (1). Задача полностью решена.
Предложено расчетно-графическое задание “Динамическое сопряжение двух окружностей”. Выполнение задания требует некоторой общеобразовательной подготовки по математике в пределах 1 курса технического вуза. Для кого предназначено это задание? Для учащихся. Мы все – учащиеся! Не только сопливые студенты-первокурсники, но и молодые или убеленные сединами преподаватели, научившиеся делать 3D-макеты и полагающие на этом основании, что жизнь удалась. Осталось только следить за обновлениями графических пакетов и файлообменников, и будешь грамотным специалистом, уверенно внедряющим ИКТ в учебный процесс.
Вообще компьютерная графика в учебном процессе – очень удобная штука. Как для студентов, так в особенности она удобна для преподавателей ГГП. Раньше молодого преподавателя спрашивали на стажировке, что такое омбилические точки, соприкасающийся параболоид, индикатриса Дюпена и тому подобные скучные и непонятные вещи из кандидатского минимума по специальности 05.01.01. Теперь все это не надо знать. Не востребовано. Преподавателей ГГП даже не интересует, что такое B-сплайны или NURBS-кривые, являющиеся основой современной КГ. А зачем?
Мы все прекрасно знаем, чему надо учить и что надо знать, а что не надо. Путь совершенно простой и четкий: 3D-макет – станок. Поэтому надо учить 3D. В легких, средних и тяжелых САПР.
Это гносеологический тупик. Это подмена учебного предмета средствами для его изучения! Король – голый! Что было актуально и свежо десяток лет назад, сегодня отдает рутиной. Под девизом “учить тому, что надо будущему современному специалисту” скрывается простая человеческая лень и нежелание понять, что у нас общеобразовательный предмет, а не курсы специализированных САПР разной тяжести.
В связи с вышеуказанным, предлагается собрать полсотни заданий по инженерной компьютерной графике с практическим наполнением, подобным рассмотренным на конференции. Собирать, обсуждать, обмениваться заданиями, адаптировать их для учебного процесса. Например, такая тема – моделирование поверхности, проходящей через заданный контур. Здесь десятки учебно-практических задач! Только не надо loft.
Компьютерная графика – чрезвычайно мощный и точный геометрический инструмент. Использовать его лишь для 3D-моделирования и анимаций означает остановку в развитии ГГП с явной, уже сегодня очень заметной, деградацией общегеометрического уровня как студентов, так и преподавателей.
1. Иванов Г.С. Конструирование технических поверхностей / Г.С. Иванов. – М.: Машиностроение, 1987. – 192 с.
2. Короткий В.А. Учебное задание “Плоские обводы” / В.А. Короткий, Т.Ю. Попцова // Качество графической подготовки: проблемы, традиции и инновации: Материалы VII международной Интернет-конференции. Февраль - март 2017 г. Пермь, 2017.
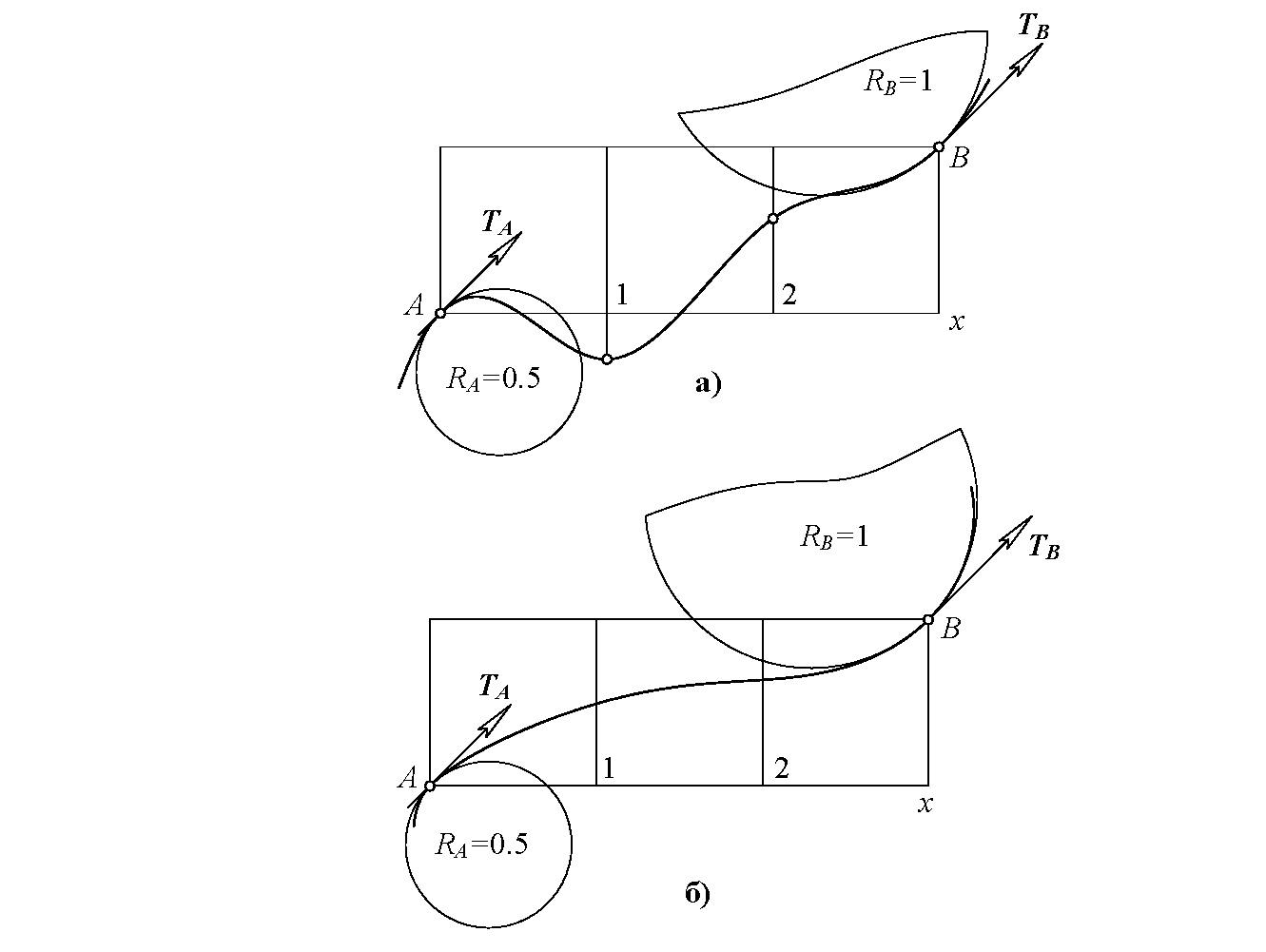
Постановка задачи и два варианта ее решения
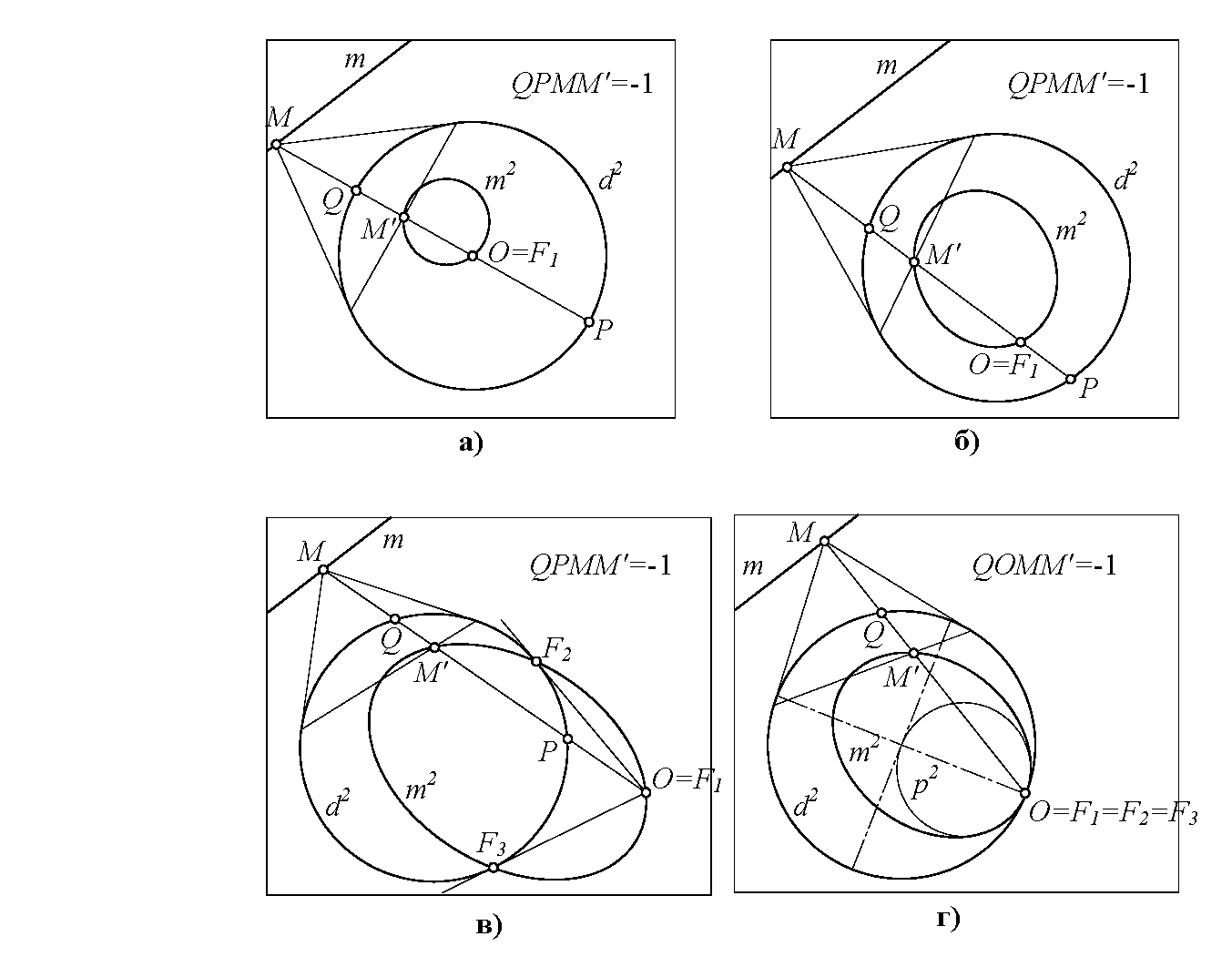
Обобщенная инверсия
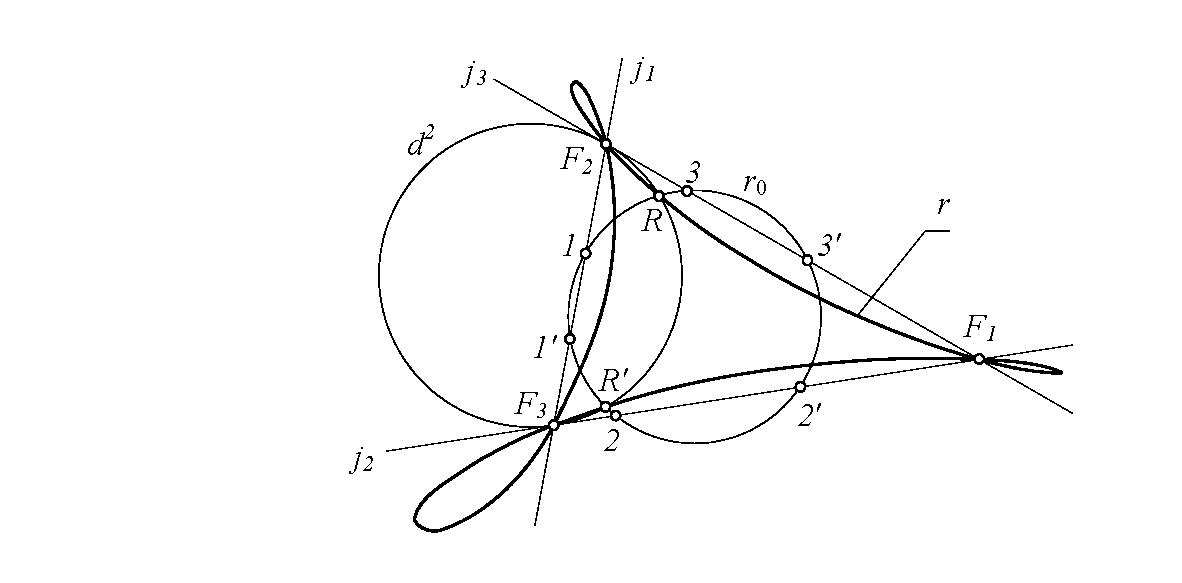
Образ окружности в обобщенной инверсии
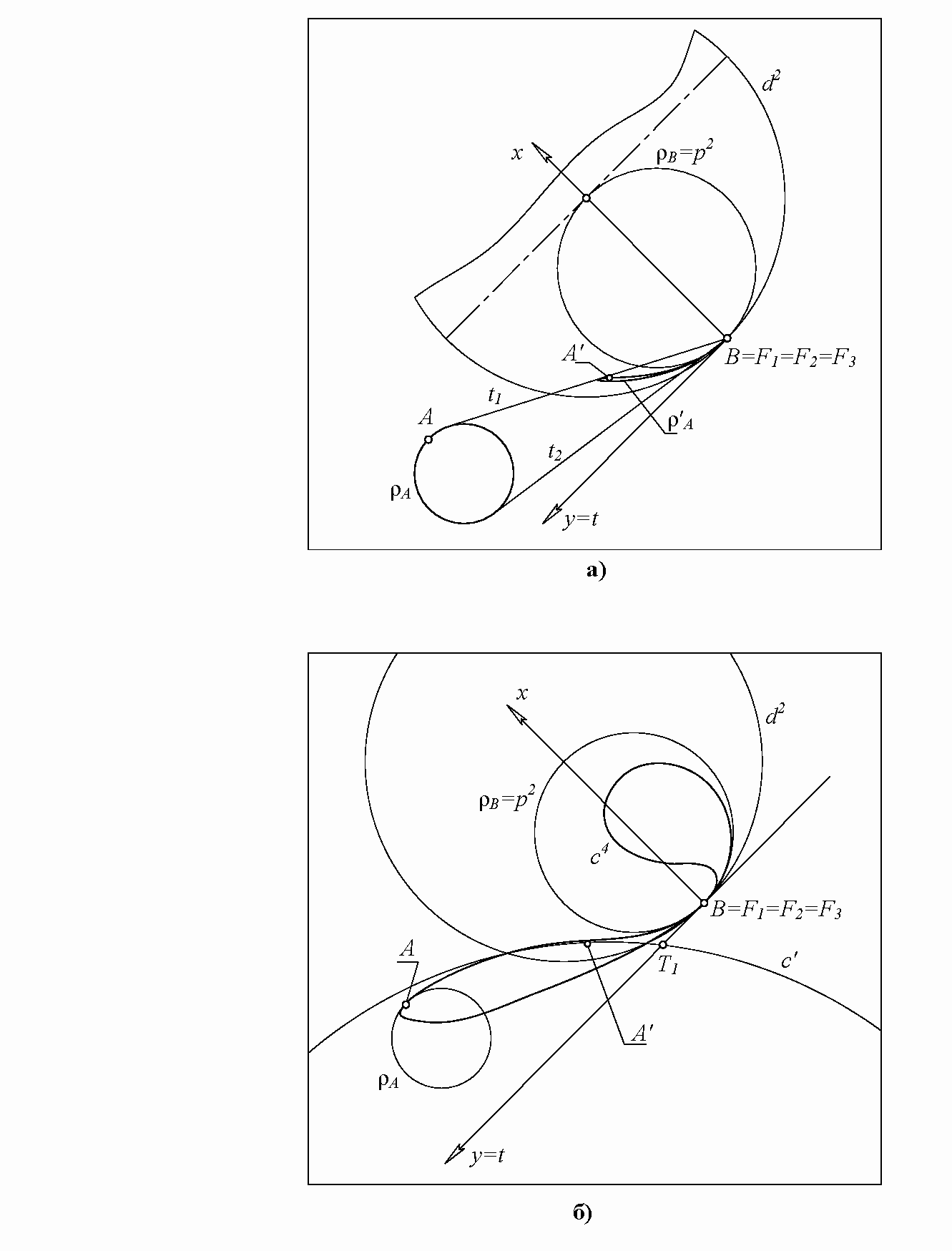
Конструирование заданного обвода