

|
Гирш Антон Георгиевич | (Universität Kassel) |
Существуют различные способы задания квадрики с помощью геометрических элементов в различном их положении относительно поверхности. Попытки определить квадрику по её девяти точкам на сегодня не дали результата. В докладе обсуждается вопрос и предлагается решение определения квадрики в случае, когда пять точек из девяти лежат в одной плоскости.
ВВЕДЕНИЕ
Невырожденная поверхность второго порядка (ПВП, квадрика) определена, если заданы девять её точек, никакие три из которых не лежат на одной прямой и никакие шесть из которых не лежат в одной плоскости. Девять точек могут быть заданы своими координатами или графически своими проекциями на полях двухкартинного чертежа. Точки попарно могут быть мнимыми. Аналитически поверхность определена, если написано её уравнение от трёх переменных с численными коэффициентами, F(x,y,z)=0 . Графически поверхность определена, если определены её основные параметры – длины трёх её главных взаимно перпендикулярных осей: большой, средней и малой. В зависимости от положения девяти данных точек одна или две из трёх осей могут оказаться мнимыми.
Уравнение квадрики имеет девять независимых коэффициентов,
a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a14x+2a24y+2a34z+1=0,
в котором по крайней мере один из коэффициентов a11, a22, a33, a12, a23, a14 отличен от нуля. Значения коэффициентов определяются из решения системы девяти линейных относительно коэффициентов уравнений, в которые подставляются координаты данных точек.
После определения коэффициентов уравнения возможно приведение квадратичной формы к каноническому виду и построение графика поверхности в проекциях на координатные плоскости или в виде аксонометрического изображения.
КРАТКИЙ ОБЗОР КОНСТРУКЦИЙ ПОВЕРХНОСЕЙ
Аналитическое определение поверхности через написание уравнения по координатам девяти её точек возможно без особых трудностей. Но здесь нас интересуют графические конструкции. В учебной литературе описаны поверхности вращения, заданные осью и образующей линией, поверхности параллельного переноса, заданные направляющей и образующей линиями. Эллиптический гиперболоид может быть задан тремя прямыми одного семейства (задача о трансверсалях) [1]. Известны конструкции по построению сферы по четырём точкам [2] и конструкции, в которых две или две пары точек мнимые [8]. Вместо точек могут быть заданы касательные плоскости, которые опять же попарно могут быть мнимыми. Известны конструкции, в которых задаётся центр, точка или касательная плоскость сферы. Рассмотрены конструкции по построению конусов и цилиндров по их оси и паре точек или плоскому сечению, и др. [4, 5, 8]. Но нигде не встречается конструкции по построению поверхности второго порядка, исходя только из девяти её точек, возможно, таковой и не существует [11].
В курсе НГ, КГ и ИГ поверхности второго порядка задаются главными очерками и решаются задачи на построения её плоских сечений, точек пересечения с прямой линией, но основное внимание уделяется построению проекций линии взаимного пересечения двух поверхностей. Вопрос воссоздания поверхности по её фрагментам в этих курсах не ставится. На фоне достаточно скромных достижений в области геометрических конструкций в НГ и ИГ выделяется работа Глазунова Е.А. [7], в которой показаны важные проекционные свойства ПВП. Но таких работ мало. Сегодня набирает силу тренд на аналитику, машинную графику и уход в высшие измерения. Да, в 4D гораздо проще оперировать буквами, чем графическими преобразованиями геометрических образов. Тем важнее пополнять багаж свойств геометрических 2D и 3D образов, являющийся ориентиром в высших измерениях и позволяющий опираться на логику их конструкций.
В настоящей работе мы обсуждаем вопрос определения параметров ПВП – определение положения поверхности в пространстве и определение размеров её главных осей по наперёд заданным точкам или другим элементам поверхности.
ДЕВЯТЬ ТОЧЕК КВАДРИКИ
Квадрика имеет три главные оси – это три параметра. Центр квадрики может быть сдвинут от начала координат вдоль каждой из трёх осей – это ещё три параметра. Квадрика может быть наклонена к координатной оси в каждой из трёх координатных плоскостей. Итого, квадрика определяется девятью параметрами. Принадлежность точки поверхности определяется одним параметром, следовательно, девять точек определяет квадрику. Девять точек определяют квадрику по форме и по положению в пространстве. Девять точек – это три тройки точек, которые задают три плоскости, несущие эти точки. Существует 84 сочетаний из девяти по три, C39=84, и для решения задачи можно выбрать любую тройку плоскостей.
1. Все девять точек действительные.
Для построения коники по трём точкам в плоскости beta необходимо, чтобы в плоскости al было дано полное коническое сечение или его пять точек, что, с учётом подпрограммы [9], равносильно заданию коники. Плоскость be несёт три дальнейшие точки и прямую a пересечения с плоскостью alpha. Коника q1 в плоскости alpha определяет на ребре a инволюцию. По трём точкам и инволюции на ребре a строится коника q2. Три точки можно выбрать из четырёх оставшихся как одно из возможных сочетаний, C34=4.
Получается перераспределение точек по плоскостям к изначально намеченным тройкам. Плоскость alpha несёт пять точек, плоскость beta несёт три точки, а третья плоскость gamma несёт одну точку.
Построения коники q2 и коники q3 опирается на свойство пучка конических сечений, получаемых от сечения поверхности второго порядка пучком плоскостей.
Предложение. Если пучок плоскостей пересекает поверхность второго порядка, то все конические сечения пучка высекают на оси пучка одну и ту же инволюцию.
Если ось пучка реально пересекает поверхность, то инволюция на оси гиперболическая, если не пересекает – эллиптическая.
Доказательство. Если ось пучка плоскостей пересекает поверхность второго порядка, то все кривые пучка пересекают прямую в тех же точках, что и сама прямая (сама прямая может рассматриваться как предельная коника пучка). Эти точки будут двойными для гиперболической инволюции на прямой. Если прямая не имеет с поверхностью реального пересечения, то она имеет с ней мнимое пересечение и мнимые точки пересечения будут являются двойными точками эллиптической инволюции на прямой.
Отметим сходство сформулированного предложения 3D-пространства со второй теоремой Дезарга 2D-пространства:
Коники одного пучка высекают на некоторой прямой одну и ту же инволюцию.
2. Часть данных точек попарно мнимые сопряжённые.
Девять почек, как сказано выше, образуют три группы по три точки. В каждой группе пара точек могут быть мнимыми сопряжёнными, следовательно, в задании квадрики может быть допущено присутствие трёх пар мнимых точек, т.е. шесть. Пара мнимых точек лежат на действительной прямой-носителе. Действительные точка и прямая задают плоскость. ПВП задана тремя плоскостями, каждая из которых несёт три точки – одну действительную и пару мнимых.
РЕКОНСТРУКЦИЯ КВАДРИКИ ПО ДЕВЯТИ ТОЧКАМ
Пусть в пространстве существует (условная) квадрика, которая пересекается тремя плоскостями alpha, beta, gamma по трём условным коническим сечениям (коникам) q1, q2, q3, каждое из которых задано тремя точками. Две смежные плоскости имеют общее ребро a, b, или c, на котором лежащие в них коники индуцируют одну и ту же инволюцию. Наличие инволюции эллиптической или гиперболической на некоторой прямой плоскости позволяет в этой плоскости по трём данным точкам построить ещё две действительные точки коники. Если убрать условности по поверхности и по коникам, то в остатке остаётся трёхгранник с тремя рёбрами a, b, c и тремя точками в каждой грани. Конструкцию несложно себе представить и без чертежа. Что дальше? А дальше ничего. Нам не известны геометрические конструкции и теоремы, базирующиеся на проективности, которые бы позволили определить инволюцию на общем ребре смежных плоскостей, исходя только из трёх точек в каждой из них. На этом основании приходиться признать, что графическое построение поверхности второго порядка по девяти её точкам на сегодня не представляется возможным [11].
В данной задаче аналитический подход имеет преимущество перед графическим – коэффициенты уравнения квадратичной формы могут быть вычислены по координатам девяти точек решением системы девяти линейных относительно коэффициентов уравнений, а графический подход по воссозданию поверхности по проекциям девяти её точек даёт сбой. Это, конечно, не повод игнорировать графические способы решения задач, имеющие преимущество в других случаях. Геометры всё же видят графическое решение поставленной задачи через квадратичные преобразования и здесь трудно будет убедить решающего отказаться от аналитического решения в пользу графического.
ЗАДАНИЕ КВАДРИКИ КОНИКОЙ И ЧЕТЫРЬМЯ ТОЧКАМИ
РЕКОНСТРУКЦИЯ КВАДРИКИ ПО КОНИКЕ И ЧЕТЫРЁМ ТОЧКАМ
1. Квадрика задана коникой q1 и четырьмя точками 1, 2, 3 и 9. Если считать, что коника задаётся пятью точками, то, в общей сложности, квадрика задана девятью точками из условия, что никакие три не лежат на одной прямой, рис.1. Коника q1 лежит в плоскости alpha, через точки 1, 2, 3 проведена плоскость beta. Плоскости пересекаются по прямой a. Коника q1 не пересекает прямую a, но индуцирует на ней эллиптическую инволюцию sigma с парой мнимых точек. Построение мнимых точек и маркера delta на прямой a показано на рис. 2a.
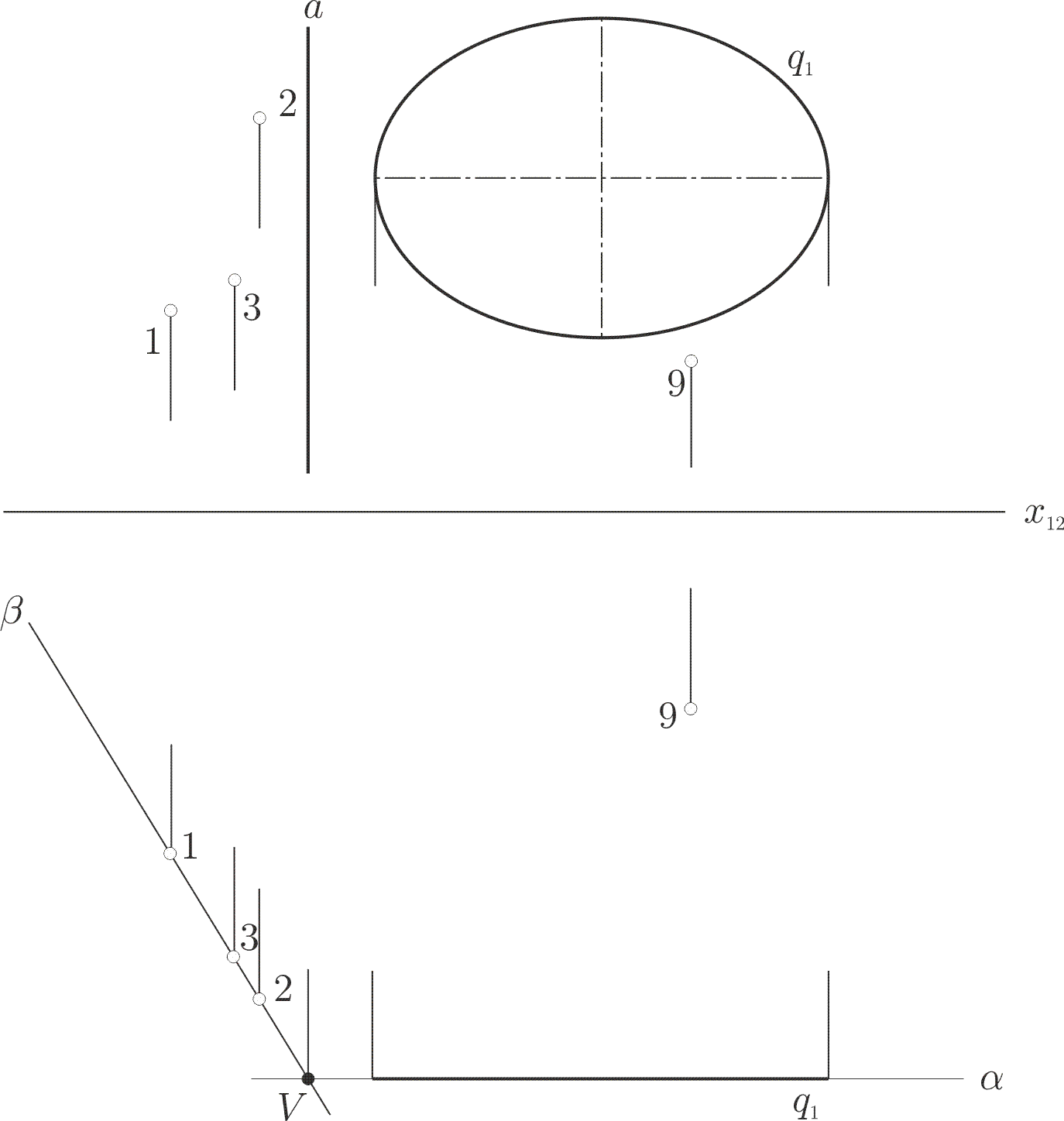
Рис. 1
2. Большая ось коники q1 пересекает прямую a в точке O. Из точки O проводят касательные к конике q1 и из конца большой оси коники через точки касания проводят прямые (пунктирные линии) до пересечения с прямой a в двойных точках инволюции. Двойные точки удалённые от точки O на расстоянии delta. Строят маркер инволюции – отрезок длинной delta, перпендикулярный носителю v в центре O инволюции.
3. В плоскости be даны три точки 1, 2 и 3 и прямая a с инволюцией sigma. Это позволяет в плоскости beta построить ещё две недостающие точки 4 и 5 для второй коники q2 как сечения искомой квадрики плоскостью beta, рис. 2 b.
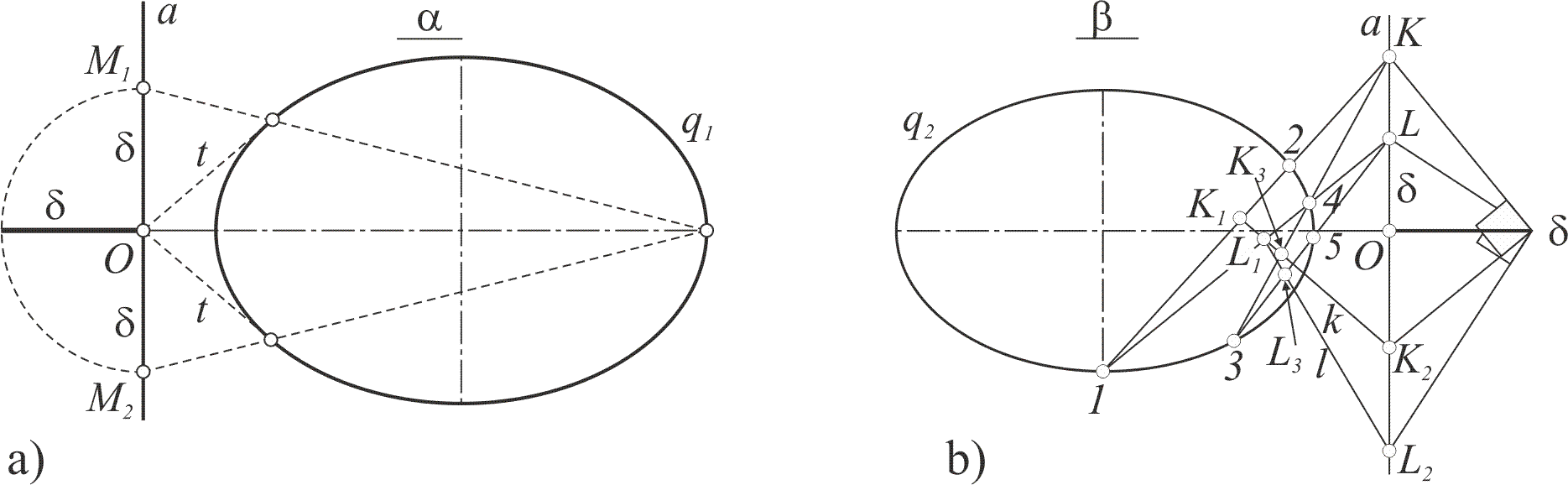
Рис. 2
а) K=12•a. K1~(1,2; K) , K1 – четвёртая гармоническая точка к тройке точек 1, 2, K. K2~K в инволюции sigma, угол KdeltaK2 прямой. k=K1K2. K3=k•3K, 4~(K,K3; 3), 4 – четвёртая гармоническая к тройке точек K, K3, 3 и четвёртая действительная точка коники q2.
b) L=14•a. L1~(1, 4; L). L2~L в инволюции sigma. l=L1L2. L3=l•3L. 5~(L, L3; 3), 5 – пятая действительная точка коники q2.
Итого, для коники q2 в плоскости be построены пять действительных точек. Достаточно плотный ряд точек коники может быть построен по теореме Паскаля [3] или, если построение выполняется в пакете AutoСАД, то, с применением VLISP-программы В.А. Короткого [9], коника представляется непрерывной линией с указанием главных осей и, в случае гиперболы, с указанием асимптот.
4. Через девятую точку 9 проводят плоскость gamma, перпендикулярную общему ребру a плоскостей alpha и beta. В условиях примера плоскость gamma не пересекает коники q1 и q2. Прямые alpha' и beta' как следы плоскостей alpha и beta на плоскости gamma несут эллиптические инволюции от коник q1 и q2, что определяет для коники q3 в плоскости gamma пять точек, данную точку 9 и по паре мнимых точек на следе alpha' и на следе beta'. Построение четырёх недостающих действительных точек см. на рис. 3:
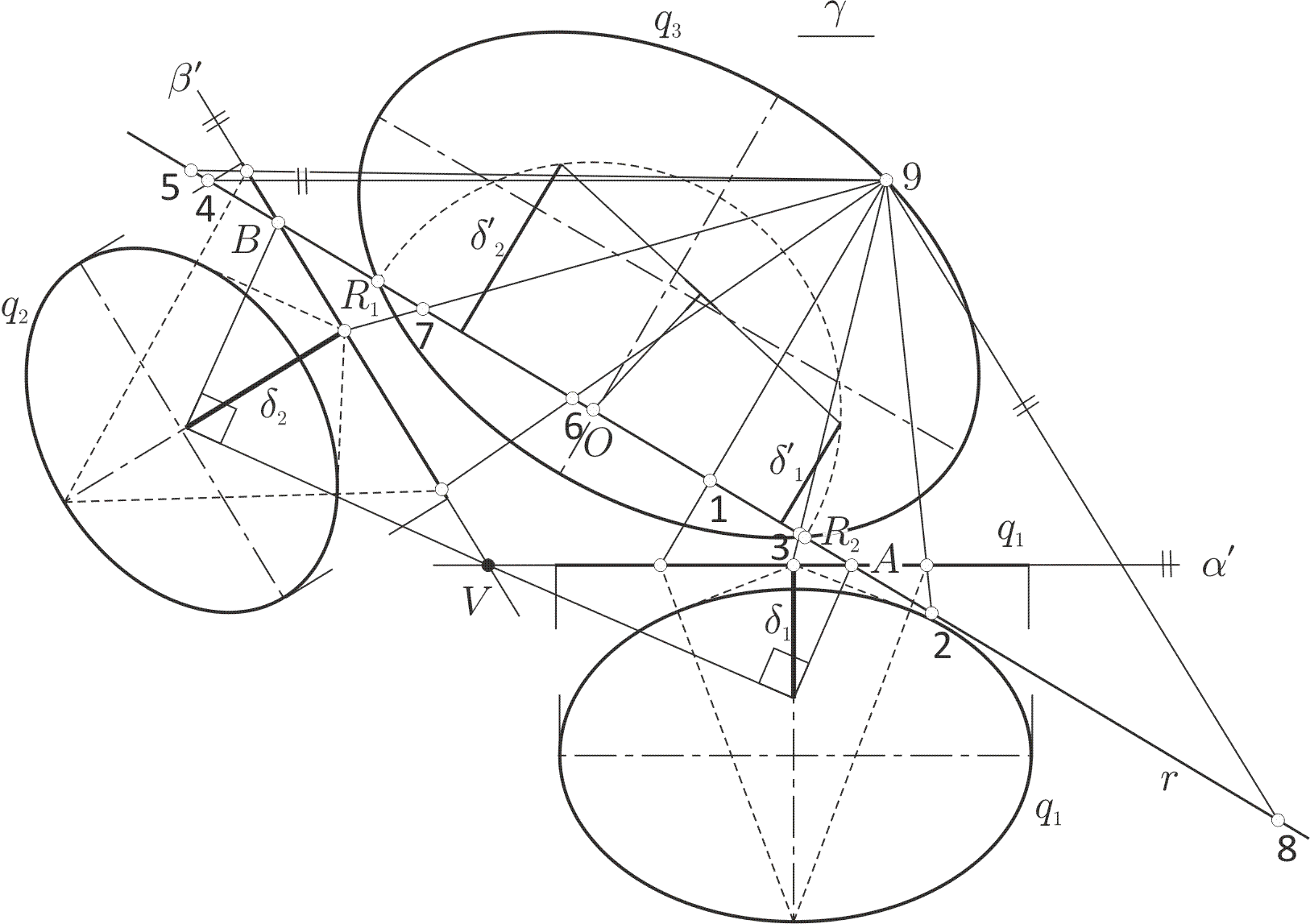
Рис. 3
а) Коники q1 и q2 совмещают с плоскостью ga поворотом вокруг следа alpha', соответственно вокруг следа beta'. Для каждой коники на её следе определяется центр инволюции и двойные точки (по конструкции рис. 2 а штриховые линии) и строятся маркеры delta1 и delta2.
b) Следы alpha' и beta' пересекаются в точке a'. Строят точку A, соответственную точке V в инволюции на alpha', строят точку B, соответственную точке alpha' в инволюции на beta'. Через точки A и B проводят прямую r. Прямая r есть поляра точки V относительно искомой коники q3, проходящей через точку 9.
с) Из точки 9 проецируют инволюционную четвёрку точек с прямой alpha' в точки 12÷34 на прямой r и четвёрку точек с прямой beta' в точки 56÷78 на прямой r. На прямой r расположились две эллиптические инволюции с маркерами delta'1 и delta'2. Две эллиптические инволюции на общем носителе имеют две общие действительные двойные точки R1 и R2. Они лежат в пересечении окружности (штриховая линия) с центром на прямой r, проходящей через вершины маркеров delta'1 и delta'2. Искомая коника q3 задана тремя действительными точками R1, R2, 9 и парой мнимых точек на носителе alpha' или beta'.
d) Построение двух недостающих до пяти действительных точек выполняется по алгоритму п.2 а и b, рис. 2 b.
5. Для искомой квадрики построены три плоских сечения q1, q2 и q3. Квадрика будет определена, если будет построен её центр C и, как минимум, пара очерков.
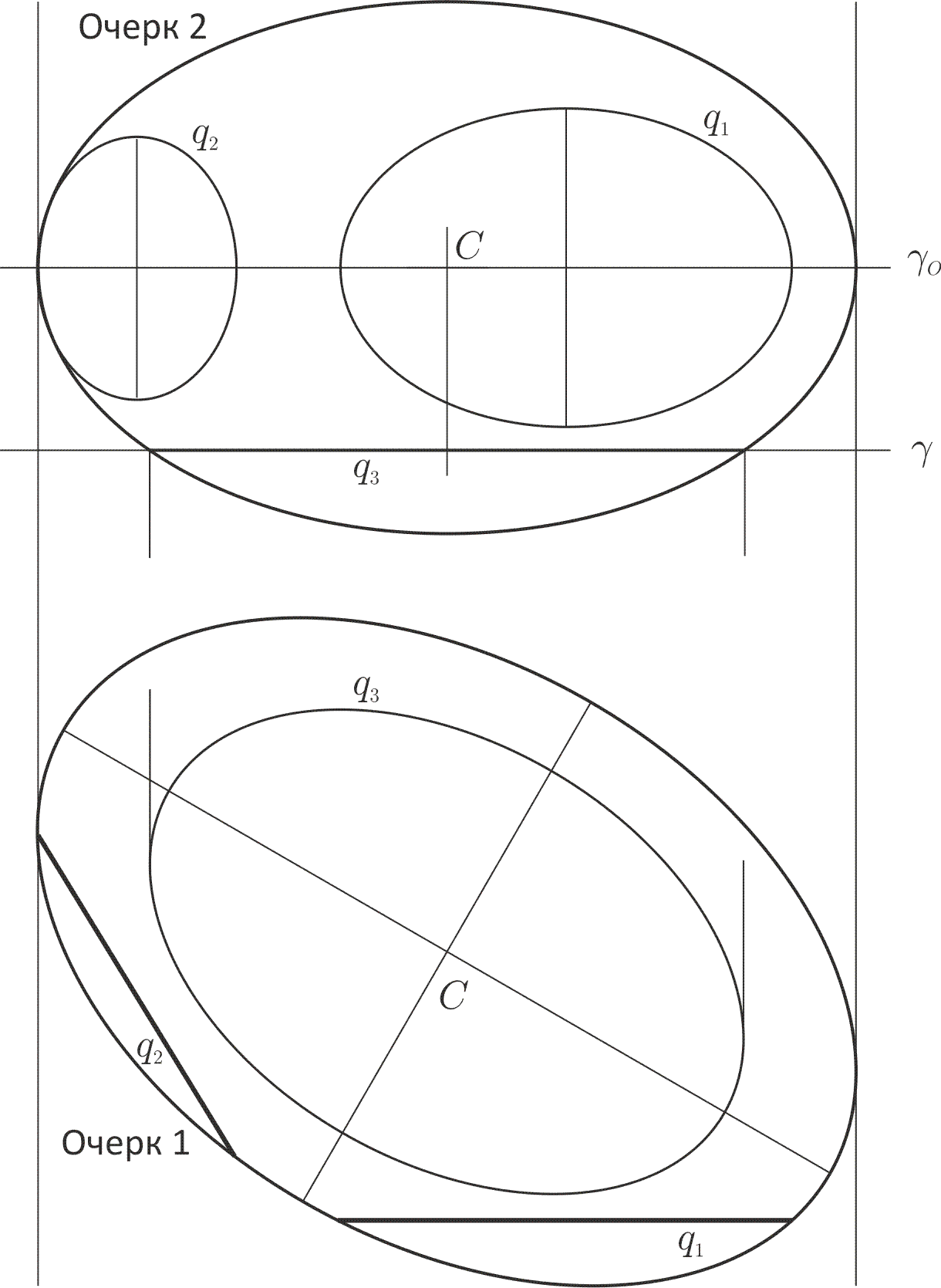
Рис. 4
ВОПРОСЫ РЕКОНСТРУКЦИИ КВАДРИКИ ПО ТРЁМ ЕЁ СЕЧЕНИЯМ
Определяют ли три произвольно выбранные в пространстве коники квадрику? Если да, то решение будет единственным или их будет несколько? Уточнить вопрос можно через геометрический эксперимент. В пространстве выбирают некоторую квадрику и делают на ней три произвольных сечения. Затем квадрику убирают, а сечения оставляют. Вопрос: как по трём сечениям квадрики реконструировать саму квадрику? Возможна ли реконструкция поверхности на проекционном чертеже или реконструкция возможна только как 3D компьютерная модель?
Коники q1, q2 и q3 лежат в плоскостях, соответственно alpha, beta и gamma. Три плоскости образуют трёхгранник с ребрами a, b, c и вершиной V. Встаёт вопрос, существует ли квадрика, несущая три произвольно взятые в пространстве коники? Ответ отрицательный. Чтобы коники лежали на общей квадрике, они не могут быть выбраны произвольно, а должны удовлетворять следующему условию. Коники q1, q2 и q3 должны попарно на общем ребре a, b или c определять одну и ту же инволюцию – на ребре a коники q1, q2 определяют инволюцию sigma12, на ребре b – инволюцию sigma23, на ребре c – инволюцию sigma13.
Строят точку Va на ребре a, точку Vb на ребре b и точку Vc на ребре c, соответственную точке V в инволюции на ребре. Три точки Va, Vb, Vc определяют плоскость phi, соответственную точке V в поляритете относительно квадрики kappa. Плоскость phi пересекает каждую из коник q1, q2 и q3 в паре точек. Точки определяют четвёртую конику q4 в полярной плоскости phi.
Пусть даны коника q, прямая a и точка V на прямой a. Коника индуцирует на прямой a инволюцию sigma. Справедливо следующее предложение:
Поляра p точки V относительно коники q проходит через точку V' , соответствующую точке V в инволюции sigma на прямой a.
Доказательство. Соответственные точки в инволюции на прямой a строятся либо как точки в полярном соответствии, точка V → коника q → поляра p → точка V', либо непосредственно на прямой a, минуя конику q, V → маркер delta → точка V'.
Важное свойство: Если C4 центр коники q4 в полярной плоскости phi, то прямая VC4 проходит через центр C искомой квадрики. Вторую центральную прямую и центр C как точку их пересечения можно получить, если для плоскости beta выбрать другую тройку точек.
ЗАКЛЮЧЕНИЕ
Пять точек плоскости, никакие четыре из которых не лежат на одной прямой, определяют кривую второго порядка. Теорема Паскаля даёт правило по сколь угодно плотному загущению точек кривой. Великие геометры делали попытки найти аналог теоремы Паскаля по построению поверхности второго порядка по исходным девяти точкам. Поиски не дали результата [11]. В докладе рассмотрены некоторые аспекты этой проблемы.

Селиверстов Александр Владиславович (2 марта 2017 г. 19:16) |
Здравствуйте, Антон Георгиевич! Здесь рассмотрение мнимых точек или гиперпболоидов вместо эллипсоидов почти ничего не меняет: трудная задача не становится легче. |

Гирш Антон Георгиевич (2 марта 2017 г. 22:30) |
Александр Владиславович, здравствуйте. Я по молодости пытался некоторые аналитические операции повторить в геометрических построениях. Тогда не очень успешно. Вы напомнили о таком подходе, можно будет снова попытаться. Да, конечно, речь не о том, чтобы просто и элегантно решить задачу построения поверхности по её девяти точкам, а о том решается ли задача вообще . Принципиально да или нет. Громоздко - это тоже решение. Спасибо, Вы увидели свет в конце тоннеля. С уважением. Антон Г. Гирш. |

Хейфец Александр Львович (3 марта 2017 г. 21:06) |
Здравствуйте, Антон Георгиевич. Построение квадрики по ее 9-ти точкам, как и Вы, считаю важной и интересной задачей, и, извините за нескромность, также занимаюсь ее решением. К обозначенной теме можно добавить работу уважаемого В. А. Пеклича, в мемуарах которого (см. интернет) есть его воспоминание о решении задачи на построении конуса 2-го порядка по четырем точкам и двум касательным плоскостям. Есть две его статьи по этой задаче (см. Сборник научно-методических статей по начертательной геометрии и инженерной графике. Вып. 9 , М.: Высшая школа , 1982, и то же, вып. 10, 1983). Правда, в них, как и у Вас, лишь обсуждение проблемы и подсчет параметров, показывающий возможность решения. Само решение отсутствует, хотя есть ссылка на его реализацию в недоступной литературе (трудах МАИ). Если считаете возможным, прошу ответить на два вопроса. Они близки между собой и возникли в связи с высказанным здесь Александром Владиславовичем комментарием. Вопрос первый. Рассматривая обобщенную теорему Данделена, ее геометрическое доказательство, я пообщался с математиками и наткнулся на их насмешку: зачем нужны геометрические доказательства, если существуют известные аналитические доказательства. Это относиться и к теореме Данделена и ко многим другим нашим задачам, в том числе, и к задаче построения квадрики по ее 9-ти точкам. Ведь считается, и Вы это отмечаете во введении, что аналитическое решение этой задачи вполне доступно. Заодно понял, что наша начертательная геометрия для математиков, как раздел математики, не существует. Но это замечание мимоходом. Итак, зачем нужны геометрические решения, если известны соответвующие аналитические решения. Как бы Вы ответили на этот вопрос? И второй вопрос. ( С уважением. А.Л. Хейфец. |

Селиверстов Александр Владиславович (4 марта 2017 г. 1:13) |
Здравствуйте, Александр Львович! Тривиальный и шутливый пример: вычисление точки касания двух вещественных сфер с данными центрами и радиусами, очевидно, сводится к решению системы нелинейных алгебраических уравнений. Ой! Ох, придётся вычислять базис Грёбнера... Но ведь эта точка лежит на прямой, проходящей через центры сфер. И сразу всё стало просто! Чуть-чуть серьёзнее: построения циркулем и линейкой можно преобразовать в алгоритм, в котором на промежуточных вычислениях все числа либо рациональные, либо представимы периодическими цепными дробями. 2) Новые доказательства известных теорем необходимо публиковать, если они дают эффективный алгоритм или новый подход к другим задачам. И мой комментарий об эллипсоиде не означает, что красивое геометрическое доказательство никому не нужно. Даже если доказать удаётся лишь частный случай. PS Мне не приходилось рецензировать статьи из ГиГ. |

Хейфец Александр Львович (4 марта 2017 г. 10:09) |
Александр Васильевич, здравствуйте. Пока не пришел ответ Антона Георгиевича, отвечу Вам шутливой репликой. "Если для аналитического решения геометрической задачи придется вычислять "базис Гребнера", то с аналитикой лучше не связываться". Теперь чуть серьезнее. В 70-е годы обсуждалась проблема разработки программного обеспечения к "тем" компьютерам на основе алгоритмов начертательной геометрии. Это отражено в работах Сергея Аркадьевича Фролова. Но эта идея не прошла, и аналитика в программном обеспечении окончательно победила геометрические методы циркуля и линейки. Об этом много дискутировали на предыдущих конференциях (см. http://dgng.pstu.ru/conf2015/papers/72/ и http://dgng.pstu.ru/conf2016/papers/74/ ). Сейчас циркуль и линейка возвращаются в форме параметризации, применяемой в современных графических САПР. С ее помощью удается геометрически решить недоступные ранее задачи или значительно упростить ранее известные решения. На эту тему мною опубликована большая статья: “3D модели и алгоритмы компьютерной параметризации при решении задач конструктивной геометрии (на некоторых исторических примерах)”. Эта статья Вам знакома, она в Вашем докладе проходит как [17] (признателен за цитирование). Но все-таки приведу ее адрес: https://vestnik.susu.ru/ctcr/article/view/4909/4293 , может еще кто-то прочтет. (Кстати, эту статью из-за позиции редакции мне не удалось опубликовать в “ГиГ”). Конечно, параметризация – это не те явные циркуль и линейка, о которых говорят и мечтают мои оппоненты. Это современный 3d инструмент компьютерного 3d геометрического моделирования, Это аналитическое программное обеспечение с удобным графическим интерфейсом. Теперь к обсуждаемому вопросу о связи аналитики и геометрических методов. Видимо в явном виде аналитика не для нас, хотя я помню заветы великого Гаспара Можа о совместном преподавании аналитической и начертательной геометрий (НГ). Но за прошедшие 220 лет такого слияния не произошло и уже не произойдет (помните академика А.П. Танукова “зачем преподавать умирающие дисциплины”. Это о НГ). Однако с учетом параметризации считаю, что косвенно слияние аналитики с геометрией все-таки происходит в форме 3d параметризации. То есть параметризация – это и есть такое слияние, в котором постановка задачи и алгоритм решения геометрические, а реализация – аналитическая. Что Вы об этом думаете? Надеюсь, Антон Георгиевич не очень сердится, что мы расположились на его поле. Вообще, получилось, что мой вопрос о связи аналитики и геометрии риторический (“сам пою, сам танцую”). С уважением. А.Л. Хейфец. |

Хейфец Александр Львович (4 марта 2017 г. 10:34) |
Александр Владиславович, извините за ошибку в Вашем отчестве. Просто, мы еще мало знакомы, а очки не надел. С уважением. А.Л. Хейфец |

Селиверстов Александр Владиславович (4 марта 2017 г. 15:06) |
Александр Львович! |

Гирш Антон Георгиевич (5 марта 2017 г. 0:41) |
Уважаемые Александр Львович и Александр Владиславович, здравствуйте. Нет, я непротив дисукссии здесь и даже наоборот прятно читать доводы столь серьёзных мужей. С работами В.А.Пеклича знаком, он решил порядка 70 задач на определение квадрик при различном их задании, кроме задания точками. Решения давал геомтрические. Идею Г. Монжа о совместном изучении аналитики и геометрии в 70-х годах пытались реализовать в МАИ (поф. И.И.Котов). Но быстро отказались! Почему? Потому что аналитика подавляла геометрию. Геометрические алгоритмы более громоздки и трудоёмки, чем аналитические и, понятно, студенты предпочитали что попроще. Но умение мыслить геометрическими образами инженеру нужно и это умение надо воспитывать. Начертательная геометрия при всей её, казалось бы, примитивности даёт такоё опыт. Речь же об подготовке инженеров, а не математиков. У последних вырабатывается совсем другой стиль мышления. Это к первому вопросу. Второй вопрос - как из той песни "мамы всякие важны, мамы всякие нужны". Беусловно ценится корректное доказательство. Интересны и разные подходы в решении одной и той же проблемы. |

Селиверстов Александр Владиславович (6 марта 2017 г. 20:24) |
Здравствуйте, Антон Георгиевич!
|

Гирш Антон Георгиевич (7 марта 2017 г. 0:55) |
Александр Владиславович, это было так давно. Статья печаталась и у Денискина Ю.И (МАИ). в его электорнном журнале apg.ru. Тогда я искал приложение комплексных образов в геометрии и дал доказательство теоремы Вилларсо с их участием, иначе, учёл число мнимых точек. Вас привлекло обобщнение в заключение статьи " Заключение В данной статье нами показано одно обобщение понятия "сечения Вилларсо" путём замены образующего круга традиционного открытого тора на образующую конику поверхности вращения. Это, в свою очередь, расширило метрическое пространство в область мнимого. Приведённые примеры показывают свойства v-сечений, сформулированных в приведённых теоремах, как в действительном пространстве, так и в области его мнимого продолжения и далеко идущие геометрические зависимости. В статье мы показали, что есть смысл учитывать мнимые фигуры и мнимые продолжения действительных фигур в геометрических исследованиях. Существуют различные пути обобщения конструкций как и в любом движении от простого к сложному. В данном случае укажем на возможность коллинеарного преобразования тороподобных поверхностей вращения в циклиды Дюпена или, к примеру, на возможность опустить требование к образующей конике лежать в осевой плоскости." Если будет желание, могу переслать её Вам. С уважением. Антон Г. Гирш. |

Хейфец Александр Львович (7 марта 2017 г. 7:07) |
Антон Георгиевич, позвольте два вопроса. В связи с Вашем воспоминанием о неудачном эксперименте в МАИ по совместному преподаванию аналитической и начертательной геометрий. Неудачном, поскольку аналитика подавляла геометрию. Правильно ли я понял, что построить линию пересечения, например конуса и сферы, решив систему нелинейных уравнений, оказалось студентам проще, чем применить наш родной способ секущих поверхностей? Или что Вы имели ввиду. А в целом информация важная. Ведь и здесь на конференции есть доклад Г.С. Иванова о совместном преподавании этих геометрий на наших кафедрах. О Вашей статье по тору. Может, на нее есть электронная ссылка. Будет многим интересно. А.Л. Хейфец.
|

Селиверстов Александр Владиславович (7 марта 2017 г. 12:06) |
Антон Георгиевич! Не стесняйтесь напоминать о Ваших красивых работах. Они могут пригодиться студентам и преподавателям геометрии.
|

Гирш Антон Георгиевич (7 марта 2017 г. 16:16) |
Алекандр Владиславович, спасибо на добром слове. В святом писании сказано "Вначале было слово". Я ставил себе целью организовать тренд комплексных образов в геометрии - статьи, книги. Приятно наблюдать, что табу с мнимых фигур уже снято, Наши геометры уже спокойно воспринимают упоминание о мнимых элементах. Есть приверженцы: Иванов Г.С., Пеклич В.А.(был), Короткий В.А., да и Вы тоже если не с симпатией, то терпимы. Так получилось, что в анализе всё в одном котле, а в геометрии раздельно: евклидова геометрия только для действительных образов, псевдоевклидова - для комплексных. Но между этими геометриями существует неразрывная связь и это необходимо геометрам осознать. Есть намётки визуализации последних. Вслед за Остапом скажу "Лёд тронулся, господа присяжные заседатели!" |

Бойков Алексей Александрович (30 марта 2017 г. 16:34) |
Здравствуйте, уважаемый Антон Георгиевич, спасибо за интересный доклад, как всегда, посвященный непростой геометрической задаче. Кроме системы построений ЦЛ (циркулем и линейкой) можно рассмотреть систему правил Фудзиты (складок оригами), которая содержит инструмент для решения уравнений третьего порядка, то есть, в принципе, может помочь в нахождении осей эллипосида. Кроме того, взяв за основу возможность пересечения пары коник (уравнение 4 порядка) можно выйти на красивые решения других сложных задач. С уважением, А.Бойков. |