ВЕЩЕСТВЕННЫЕ КОНИЧЕСКИЕ СЕЧЕНИЯ НА КОМПЛЕКСНОЙ ПЛОСКОСТИ

Рассмотрены геометрически точные проективные алгоритмы построения кривых второго порядка (КВП), заданных смешанным набором действительных и мнимых элементов. Мнимые точки и мнимые прямые изображаются маркерами и марками. Доказана гомеоморфность четырехпараметрических множеств маркеров и марок множеству мнимых точек и мнимых прямых на комплексной плоскости. Даны примеры решения гео-метрических задач с участием мнимых точек и мнимых прямых.

Введение

Если на плоскости задана декартова система координат xy, то любая точка M имеет координаты (x, y). И наоборот, любые два числа (x, y) указывают точку на плоскости. Если числа x, y действительные, они указывают действительную точку. Если хотя бы одно из чисел x, y комплексное, получаем мнимую точку. Например, точка M с координатами x=a+jb, y=c+jd – мнимая точка. С ней сопряжена точка N(x=a-jb, y=c-jd). Через две мнимые сопряженные точки проходит единственная вещественная прямая, однопараметрическое множество (пучок) окружностей, трехпараметрическое множество конических сечений. И вообще, указание пары мнимых сопряженных точек отнимает у любой алгебраической кривой две степени свободы – точно так же, как и указание двух вещественных точек.

Плоскость, дополненная мнимыми точками, называется комплексной плоскостью [1, с. 107]. Понятие “мнимая точка” применимо только к алгебраическим многообразиям на комплексной плоскости. Неалгебраические кривые не могут быть инцидентны мнимым точкам.

Наряду с мнимыми точками на комплексной плоскости рассматриваются мнимые алгебраические кривые (с мнимыми коэффициентами). Например, прямая g с уравнением (A₁+jA₂)x+(B₁+jB₂)y+C₁+jC₂=0 называется мнимой прямой. Прямую f с уравнением (A₁-jA₂)x+(B₁-jB₂)y+C₁-jC₂=0 называют прямой, сопряженной с первой. Мнимые сопряженные прямые g, f пересекаются в вещественной точке V.

Изображение мнимых линейных элементов

Едва ли не самый главный вопрос, возникающий при геометрических построениях с участием мнимых линейных элементов (мнимых точек и мнимых прямых), связан с их изображением на чертеже. Невозможно указать мнимую точку кончиком карандаша или начертить мнимую прямую с помощью линейки. Это “недоступные” геометрические фигуры.

В начертательной геометрии накоплен опыт построений с недоступными элементами. Например, недоступную для карандаша несобственную точку указывают направлением, что совершенно не затрудняет последующие графические построения с ее участием. В курсе перспективы решают задачу проведения прямой через недоступную точку пересечения двух прямых. Следовательно, физическая недоступность элементов еще не означает невозможность их использования в конструктивных построениях.

Очевидно, в алгебре эта проблема давно решена: мнимой точке ставят в соответствие  комплексные координаты x=a+jb, y=c+jd и спокойно выполняют любые алгебраические расчеты.

Попробуем сконструировать графический аналог мнимых алгебраических образов. Пусть на плоскости дана декартова система координат x, y. Требуется сопоставить мнимым точкам M(a+jb, c+jd), N(a-jb, c-jd) вещественную геометрическую фигуру, которую можно было бы использовать при выполнении построений с участием этих точек.

По известным мнимым координатам точек M, N рассчитаем коэффициенты уравнения Ax+By+1=0 действительной прямой v=MN, и начертим ее на плоскости xy. Это делается очень просто: в уравнение Ax+By+1=0 подставляем мнимые координаты точек M, N и из полученной системы двух линейных уравнений с мнимыми коэффициентами находим коэффициенты A, B. Мнимые единицы благополучно сокращаются в процессе алгебраических преобразований. Получен предварительный результат: точки M, N инцидентны вещественной прямой v. Но положение точек на прямой v пока не определено.

Повернем исходную декартову систему координат x, y таким образом, чтобы прямая v стала осью x. Рассчитаем комплексные координаты точек M, N в новой системе координат. Координата y точек M, N становится равна нулю. Координаты x_M, x_N точек M, N на оси x=v выражаются парой сопряженных комплексных чисел x_M=e+jr, x_N=e-jr.

Теперь самое главное. Будем считать мнимые сопряженные точки M, N двойными точками эллиптической инволюции на прямой v. Найдем какие-либо две пары действительных точек, соответственных в этой инволюции, используя уравнение инволюции x₁=(kx+1)/(qx-k), где x и x₁ - координаты пар действительных соответственных точек. Для определения неизвестных коэффициентов q, k подставляем в характеристическое уравнение инволюции qx²-2kx-1=0 известные мнимые координаты x_M, x_N двойных точек M, N. Получаем два линейных уравнения с комплексными коэффициентами, из которых определяем вещественные значения q, k (мнимые единицы взаимно сокращаются в процессе преобразований). Подставляя в уравнение инволюции произвольные значения x, находим соответствующие значения x₁. В результате на прямой v=x получаем сколько угодно соответственных пар точек в инволюции с двойными мнимыми точками M, N. Инволюция вполне определена двумя парами соответственных точек, поэтому отметим только две пары R-R₁, T-T₁.

Кажется, задача графической визуализации мнимых сопряженных точек M, N, заданных комплексными координатами на комплексной плоскости, полностью решена. Нам удалось поставить в соответствие этим точкам вещественную геометрическую фигуру, состоящую из прямой v с отмеченной на ней упорядоченной четверкой точек R-R₁, T-T₁.

Такой вариант визуализации имеет два недостатка. Первый заключается в том, что точки M, N неразличимы, как неразличимы полюса магнита или контакты (плюс-минус) электрической батареи. Для идентификации полюсов или контактов в физике принимают дополнительные соглашения. В геометрии тоже приходится прибегать к такому дополнительному соглашению, вводя понятие направленной инволюции. Мы этого делать не будем, то есть примиримся с первым недостатком. Второй недостаток связан с тем, что такую конструкцию неудобно использовать в конструктивных построениях.

Второй недостаток полностью устранил А.Г. Гирш, предложив для изображения мнимых точек использовать “маркер” вместо четверки коллинеарных точек [2]. Маркер {v, L} состоит из прямой v и не принадлежащей этой прямой точки L, из которой инволюция R-R₁, T-T₁ проецируется ортогональным пучком прямых.

Такая, казалось бы, незначительная модификация дает ощутимый эффект, практически уравнивая в конструктивном смысле мнимые и действительные точки. Мнимые точки на чертеже и построения с их участием становятся простым и наглядным делом. Этот яркий эффект от небольшой модификации можно сравнить с незначительной, но совершенно революционной перегруппировкой коэффициентов кубического многочлена Фергюсона, в результате которой получена кривая Безье, ставшая основой многих CAD-систем (Corel и др.). Точно так же маркер, состоящий из одной прямой и одной точки (вместо четырех!), стал основой современной комплексной геометрии [3, 4].

Между четырехпараметрическим множеством мнимых сопряженных пар точек комплексной плоскости и четырехпараметрическим множеством маркеров действительной плоскости установлено взаимно однозначное соответствие. Всякой паре точек M(a+jb, c+jd), N(a-jb, c-jd) отвечает единственный маркер {v, L}, образованный прямой v=MN и вершиной L ортогонального пучка, высекающего на v эллиптическую инволюцию с двойными точками M, N. И наоборот, произвольно начерченному на плоскости xy маркеру{v, L} соответствует единственная пара мнимых сопряженных точек – мнимых двойных точек эллиптической инволюции, установленной на v ортогональным пучком L. Следовательно, множество вещественных геометрических фигур (маркеров) гомеоморфно множеству пар комплексно сопряженных мнимых точек.

Пусть мнимые сопряженные прямые g, f являются двойными прямыми эллиптической инволюции в пучке с вершиной V=gf. Следуя А.Г. Гиршу, будем изображать пару мнимых сопряженных прямых “маркой” в форме прямоугольника с центром в точке V. Взаимно перпендикулярные прямые, соединяющие середины противолежащих сторон марки, указывают ортогональные направления инволюции в пучке V, а диагонали марки – главные направления, симметричные относительно ортогональных. Множество марок гомеоморфно множеству пар мнимых сопряженных прямых.

Мнимые линейные элементы в геометрических построениях

Когда говорят о построениях с участием мнимых элементов, то имеют в виду графические действия, эквивалентные решению алгебраических уравнений или их систем. Например, можно найти мнимые точки пересечения алгебраических кривых, но бессмысленно ставить задачу поиска мнимых точек пересечения окружности с какой-либо трансцендентной кривой. На комплексной плоскости обитают только алгебраические многообразия.

Но зато среди алгебраических многообразий мнимые и действительные элементы выступают практически на равных. Например, с одинаковой легкостью можно провести окружность как через три вещественные точки, так и через одну вещественную точку и пару мнимых (рис. 1).

Существенное отличие состоит в том, что в паре сопряженных мнимых точек нельзя разобрать, кто есть кто (см. выше). Также не стоит забывать, что на комплексной плоскости множество пар мнимых сопряженных точек четырехпараметрично, а вещественных – двухпараметрично. В результате кривая второго порядка содержит “гораздо больше” мнимых точек, чем действительных (однопараметрическое множество действительных точек и двухпараметрическое множество пар мнимых сопряженных точек). Рассмотрим пример конструктивного построения с участием мнимых точек, заданных на чертеже своими маркерами.

Пример. Проективитет полей П, П′ задан мнимыми соответственными точками. Требуется найти в заданных полях четверку проективно соответственных действительных точек (“избавиться от мнимостей”).

Пусть мнимые сопряженные точки {n, L_n} и {m, L_m} поля П проективно соответствуют точкам {n′, L′_n} и {m′, L′_m} поля П′ (рис. 2). Для конструктивной реализации решения используются вспомогательные конические сечения, проходящие через мнимые точки (рис. 3). Условию примера удовлетворяют четыре различных проективитета, что объясняется неопределенностью порядка взаимного соответствия мнимых сопряженных точек.

Пример интересен не своей непривычной формулировкой, а демонстрацией  тех преимуществ, которые мы получаем, решая алгебраическую задачу геометрическими методами. Аналитическое решение с использованием декартовых координат сводится к формальной записи восьми линейных уравнений с комплексными коэффициентами относительно восьми неизвестных коэффициентов проективного преобразования и последующему вычислению определителей 8 порядка (мнимые единицы сокращаются в процессе алгебраических преобразований).

Можно только посочувствовать математику, взявшемуся за решение такой задачи. Используя “Маткад” или другой программный продукт, позволяющий выполнять алгебраические преобразования, он, конечно, доведет решение до числа. Но полученное решение будет не слишком точным. Эксперимент показал, что при значениях координат заданных соответственных точек в диапазоне 1…10 единиц, и выполнении расчетов с пятью знаками после запятой, финальная ошибка (абсолютная разность левых и правых частей в уравнениях проективного преобразования) составляет 0,1…0,2 единицы. А если координаты заданных точек различаются на порядки? Какая тогда будет вычислительная погрешность?

В отличие от алгебраического, геометрическое решение с использованием вспомогательных эталонно вычерчиваемых КВП (см. рис. 3) позволяет получить решение с точностью “до привязок”. Иначе говоря, проверочная точка, заданная перед началом эксперимента, совпадает с экспериментально построенной точкой с точностью, равной точности встроенного вычислителя. Ошибка не накапливается!

Дело в том, что в рассмотренном примере кривая второго порядка (вернее, геометрически точный алгоритм ее построения) выступает как своеобразная геометрическая машина, заменяющая большое количество элементарных алгебраических операций, причем работающая совершенно независимо ни от условий конкретной задачи, ни от выбора системы координат и их абсолютных значений. Применение КВП как эталонной кривой в геометрических алгоритмах эквивалентно замене последовательных вычислений (при которых арифметическая ошибка растет как снежный ком) параллельными расчетами. Почему в машиностроении размеры ставят не цепочкой, а ступенькой (от базы)? Чтобы не накапливать ошибку.     

Графические аналоговые методы технического проектирования, основанные на понятии “линия”, традиционно считавшиеся неточными, приближенными (в силу неточности чертежных инструментов, плазов, шаблонов и т.п.), на сегодняшний день не уступают в точности расчетно-аналитическим методам, зачастую превосходя их в простоте и наглядности.         

Построение КВП, заданной мнимыми линейными элементами

Существует семь пар взаимно двойственных сочетаний (специализаций) вещественных и мнимых линейных элементов, задающих КВП на комплексной плоскости (рис. 4). Для всех 14 специализаций составлены геометрически точные проективные алгоритмы, позволяющие “избавиться от мнимостей” и перейти из комплексной плоскости в действительную.

Для построения КВП на действительной плоскости следует обратиться к программному средству “Коникограф” [5]. Отличительная особенность “Коникографа” состоит в том, что конечный результат работы программы – вовсе не вычерчивание кривой второго порядка, а геометрически точное построение ее метрики (вершин, асимптот, фокусов).

Понятия “геометрически точное решение” и “точность конструктивного решения” имеют разный смысл. Геометрически точным называют решение, для конструктивной реализации которого используют лишь два графических примитива – прямую линию и окружность. Геометрически точное решение может быть выполнено тупым циркулем и кривой линейкой. Инженерная, конструктивная точность такого решения невелика.

Вместе с тем, существует очевидная связь: чем проще алгоритм, чем меньше он содержит графических примитивов, тем выше принципиально возможная точность его конструктивной реализации.

Геометрически точное решение – самое простое из возможных. Поэтому геометрически точный графический алгоритм построения метрики КВП следует признать наиболее точным в инженерном, конструктивном смысле по сравнению с другими способами решения задачи.

Кривые второго порядка – это вспомогательный инструмент, своеобразный графический эталон, применяемый в компьютерном геометрическом моделировании. Эталон должен обладать наивысшими метрологическими свойствами. Программное средство “Коникограф” вместе с пакетом алгоритмов обеспечивает эталонно точное определение метрики КВП, заданной любым непротиворечивым сочетанием действительных и мнимых линейных элементов на комплексной плоскости.

Как начертить непрерывную КВП, если построена ее метрика? Вычерчивание непрерывной КВП с известной метрикой (центром, вершинами, асимптотами, фокусами), очевидно, не представляет никакого труда, и может быть выполнено самыми разными способами в любой CAD-системе с любой требуемой точностью.

Частные случаи

Рассмотрим некоторые частные случаи сочетаний действительных и мнимых линейных элементов, задающих коническое сечение.

1. Если пара заданных мнимых точек совпадает с циклическими точками, то задача заметно упрощается, поскольку требуется построить окружность. Например, если КВП задана пятью точками, две из которых циклические, получаем задачу: построить окружность, проходящую через действительную точку и пару мнимых сопряженных точек (см. рис. 1).

2. Пусть эллипс задан тремя действительными A, B, C и двумя мнимыми несобственными точками U, W, не совпадающими с циклическими. Действительные несобственные точки на чертеже задают действительными направлениями. Мнимые несобственные точки задают направлениями мнимых двойных прямых эллиптической инволюции в пучке с вершиной в произвольной точке V. Построим прямоугольную марку этой инволюции и аффинно растянем ее в квадрат. Инволюция в пучке V стала ортогональной, а мнимые точки U, W совпали с циклическими. Точки A, B, C сместились. Проводим окружность через смещенные точки A, B, C и обратным аффинным сжатием получаем искомый эллипс.

3. Отметим экзотический частный случай, когда мнимые точки инцидентны мнимым касательным. Требуется построить КВП, проходящую через действительную точку A и касающуюся мнимых сопряженных прямых в указанных на них мнимых точках касания. Несмотря на пугающую формулировку, задача решается исключительно просто [6, с. 110].

Заключение

В результате выполненной работы кривая второго порядка стала такой же простой и эталонно точной кривой, как прямая линия и окружность. Успешное решение проблемы геометрически точного моделирования КВП, заданной любым сочетанием действительных и мнимых точек и касательных, не связано с каким-либо определенным разделом техники или какой-либо актуальной народно-хозяйственной задачей, но вносит вклад в развитие компьютерного геометрического моделирования как неотъемлемой части всех разделов современной инженерной деятельности. Это приводит к тому, что практические приложения выполненного исследования не концентрируются в каком-либо конкретном разделе техники, а могут применяться в самых разных ее отраслях.

Список литературы

1. Атанасян Л.С. Геометрия: учебное пособие: в 2 ч. / Л.С. Атанасян, В.Т. Базылев. – М.: Кнорус, 2015. – Ч. 1. – 400 с.

2. Короткий В. А. Графические алгоритмы реконструкции кривой второго порядка, заданной мнимыми элементами / А. Г. Гирш, В. А. Короткий // Геометрия и графика. 2016. Т. 4. №. 4. C. 19-30. DOI: 10.12737/22840

3. Гирш А.Г. Комплексная геометрия – евклидова и псевдоевклидова [Текст] / А.Г. Гирш. – М.: ООО ИПЦ «Маска», 2013. – 216 с.

4. Гирш А.Г. Наглядная мнимая геометрия [Текст] / А.Г. Гирш. – М.: ООО ИПЦ «Маска», 2008. – 216 с.

5. Короткий, В.А. Универсальный компьютерный коникограф / В.А. Короткий, Л.И. Хмарова // Труды 26-й Международной научной конференции GraphiCon 2016 (19-23 сентября 2016), ННГАСУ, Нижний Новгород, Россия. – С. 347-351.

6. Суворов, Ф.М. Об изображении воображаемых точек и воображаемых прямых на плоскости и о построении кривых линий второй степени, определяемых с помощью воображаемых точек и касательных. – Казань: Типография императорского Университета. – 1884. – 130 с.

Рисунки к докладу

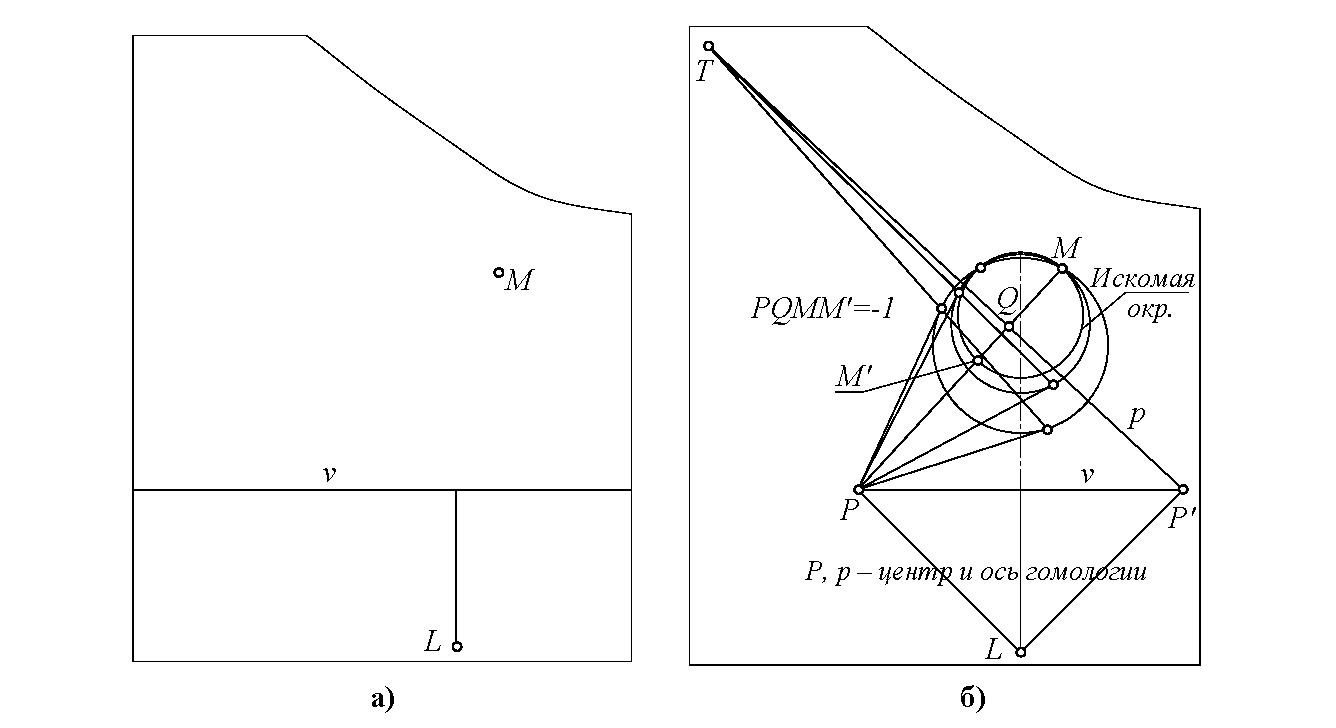
Построение окружности, заданной тремя точками, две из которых мнимые: а - исходные данные, б - решение

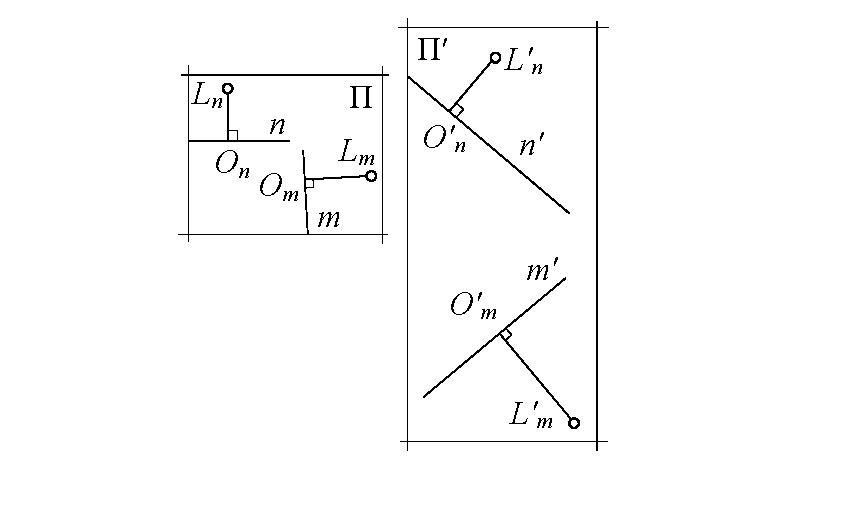
Проективитет плоских полей П, П¹, заданный четырьмя парами мнимых соответственных точек (исходные данные)

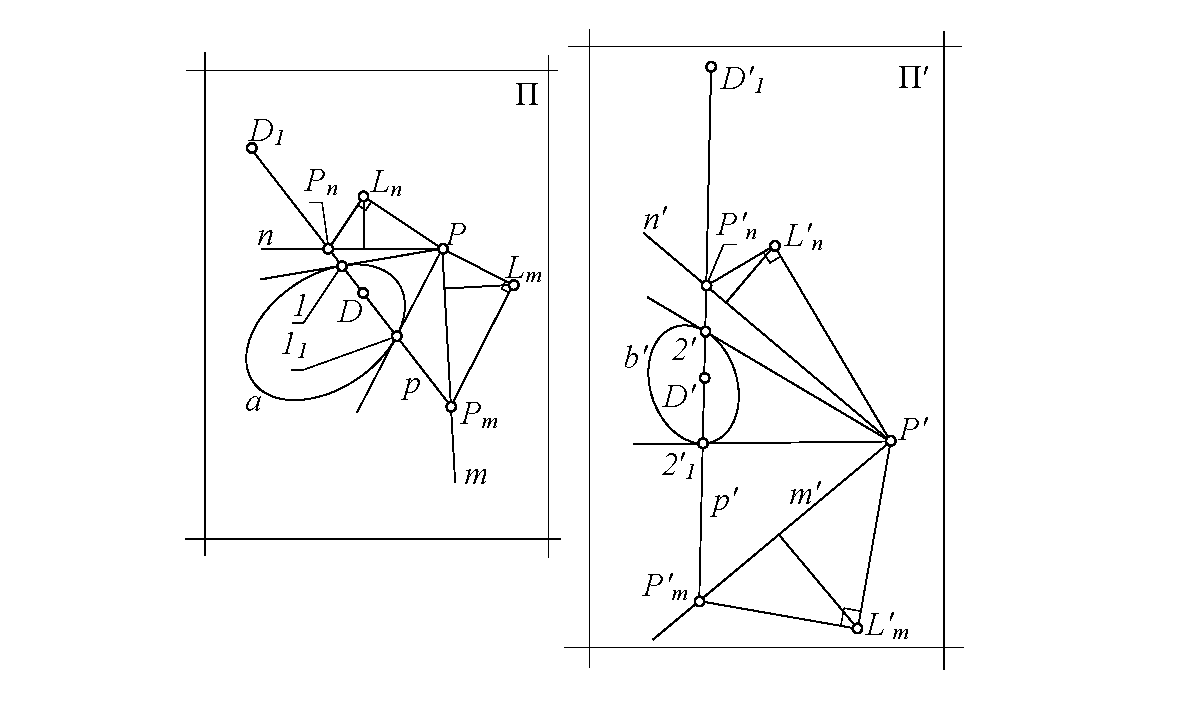
Построение соответственных точек D-D¹ в проективитете, заданном маркерами мнимых точек

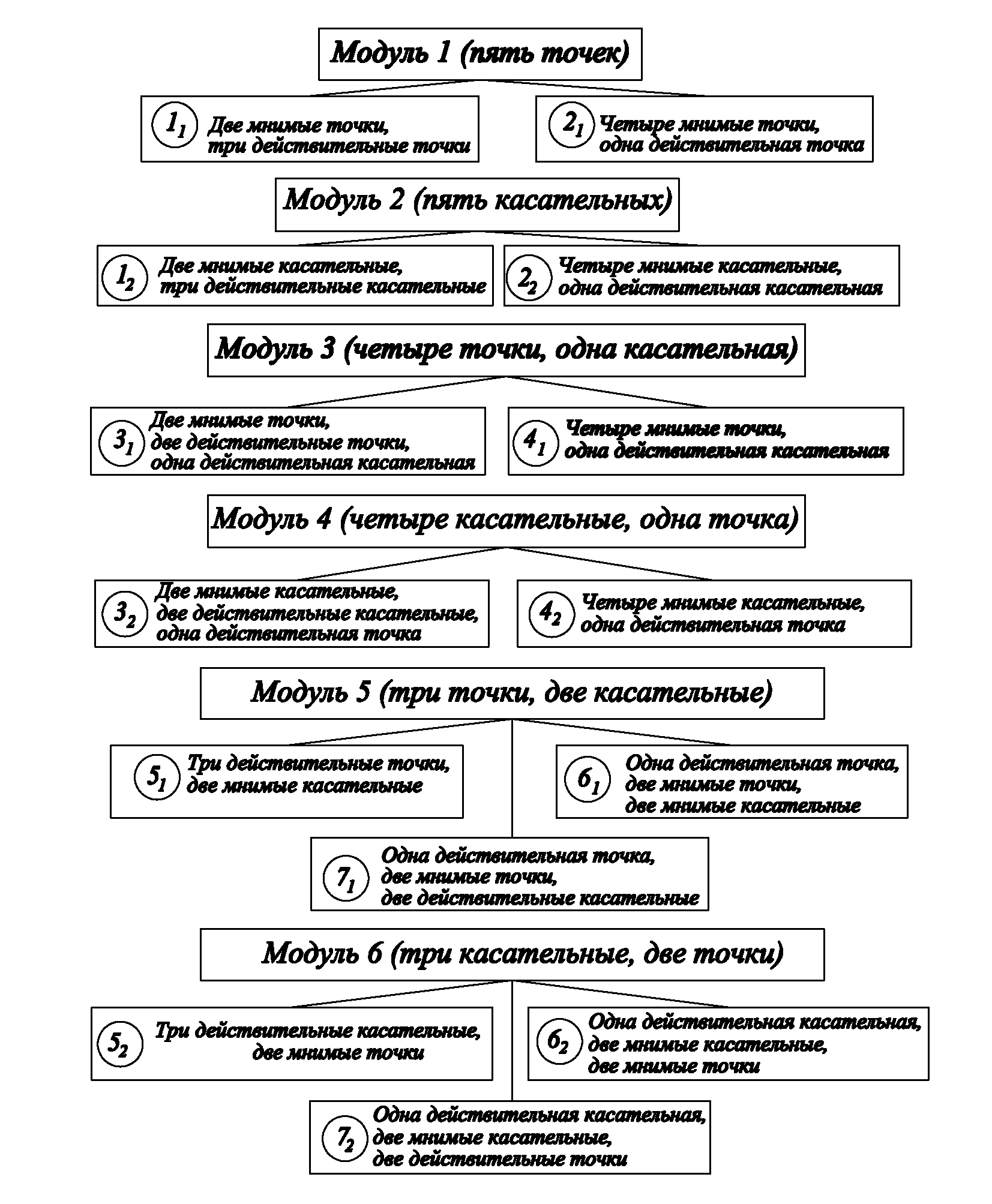
Классификатор специализаций, определяющих КВП на комплексной плоскости

Головнин Алексей Алексеевич (5 марта 2017 г. 16:28)	Здравствуйте Виктор Анатольевич! Не первый раз на конференции звучит словосочетание «геометрически точный». Вы приводите и определение этого понятия: «Геометрически точным называют решение, для конструктивной реализации которого используют лишь два графических примитива – прямую линию и окружность». Возникает вопрос – и этого достаточно, чтобы называть такие решения точными? А как же все остальные, не менее точные, достижения человечества в области геометрии? Очень спорное определение. Если мы обратимся к другим источникам информации, можно встретить, например: «Термин «геометрически точный» означает, что отсчетная поверхность оболочки описывается аналитически заданными функциями, в частности сплайнами, которые составляют основу современных CAD-систем.» (Г.М. Куликов, С.В. Плотникова, М.Г. Куликов. Связанная задача электроупругости для слоистой композитной оболочки http://apm.tstu.ru/KulikovRus/text/TSTU2010R.pdf) авторы этого определения с кафедры «Прикладная математика и механика» ГОУ ВПО «ТГТУ»; Их работа представлена в разделе «Математика. Физика» С учетом того, что геометрия – это раздел математики, работа математиков представлена на суд математиков. С учетом этого из двух сравниваемых (явно разных) определений как то больше верится им. Именно верится, и не более. В силу состава компетенций по профессиональной деятельности, преподаватель инженерной графики или, даже, начертательной геометрии (отнесены к техническим наукам) не может на достаточно профессионально оценить Вашу работу или даже хотя бы ее название. То же самое можно сказать и о других работах по многомерной и мнимой геометрии, ежегодно представляемых на конференции. Несомненно, такие публикации позволяют их авторам утвердить свой приоритет, но вот прошедшую на конференции апробацию вряд ли можно считать достаточной и интересной даже для их авторов. Слова многомерная, мнимая, повышение-понижение размерностей стали применяться даже в докладах, судя по названиям, не относящимся к этой теме, хотя еще в мемуарах В.А.Пеклича был комментарий на эту тему. Восполнить данную неувязку могло бы хотя бы взаимное оппонирование авторов по докладам на похожие темы. Вспоминается неравнодушное и честное разъяснение Антона Георгиевича Гирша, данное несколько лет назад, что эти исследования носят гносеологический характер и что нам не дано увидеть объекты четырехмерного и более пространства, а между тем такие изображения приводились. Сейчас не ищу ссылок, но они врезались в память. На сегодняшней конференции мы видим новый уровень оппонирования математической составляющей некоторых докладов в обсуждениях уважаемого Александра Владиславовича. Его выступления помогают оценить доклады, что, безусловно, очень важно как для авторов, так и читателей. Хочется поблагодарить его за большую работу и верить, что и ему эти доклады интересны, и он и в будущем будем участником. Предложение получилось выходящим за тему Вашего доклада и направленным оно получилось не только Вам, но хотелось бы видеть мотивированные обсуждения «математических» докладов специалистами (математиками по образованию, ведущими научную работу в области математики), а спустя какое-то время – популярное изложение приложений достижений такой фундаментальной науки как математика в технике. То, что изложенное применено Вами в учебном процессе или в использовано в технике, пока тоже мало верится. «… не концентрируются в каком-либо конкретном разделе техники, а могут применяться в самых разных ее отраслях» - но хотя бы один то пример можно было бы привести. С уважением Головнин А.А.
Сальков Николай Андреевич (5 марта 2017 г. 19:52)	Здравствуйте, Алексей Алексеевич! Позвольте с Вами не согласиться по поводу "точности" сплайна. Попробуйте проделать следующее: возьмите 6-8 точек, проведите в AutoCAD'е или в КОМПАС'е сплайн, а затем возьмите на этой полученной кривой точек в 2 раза больше. Результат Вас огорчит. Это будет совершенно другой сплайн, хоть точки и будут принадлежать прежнему. Чего нельзя сказать об окружности или прямой: сколько бы точек ни брали на окружности - она всегда будет той же самой окружностью. На остальные замечания пусть отвечает Виктор Анатольевич. У него должно лучше получиться.
Головнин Алексей Алексеевич (5 марта 2017 г. 20:53)	Здравствуйте Николай Андреевич! Считаю, что Ваш довод об изменчивости сплайна в случае увеличения точек вполне объясняется его свойствами. Например, для одного из наиболее общих типов сплайнов – кривых Безье степень кривой всегда на единицу меньше числа опорных точек (т.е. при трех опорных точках форма кривой - парабола) (Е.А. Снижко. Компьютерная геометрия и графика. Конспект лекций. Санкт-Петербург. 2005) Увеличиваем число опорных точек – получаем сплайн другой степени и естественно другой формы. Не берусь комментировать приведенное мной определение, данное математиками, думаю, под точностью надо понимать получение одной и той же кривой при повторении построения по одним и тем же точкам. Николай Андреевич! Я ни в коей мере не пытаюсь принизить значение результатов работы моих коллег, просто хотел сказать, что не надо бояться выставлять эти работы на суд специалистов. Думаю, мои или Ваши (мои точно) отзывы об этих работах не очень то и весомы как нематематиков. Хочется высказать пожелание приводить результаты в виде, более близком к нашей общей области интересов.  Пишу несколько резко, так как считаю что неоднократное заинтересованное и полезное (по крайней мере, для меня) личное общение с Вами позволяет это. С уважением Головнин А.А.
Гирш Антон Георгиевич (6 марта 2017 г. 0:51)	Виктор Анатольевуич, здравствуйте. Приветствую тему доклада. Ряд комплексная плоскость, мнимые расширения действительных коник, мнимые коники - это сегодня ещё в диковинку, но этим уже наметился тренд дальнейшего развития геометрии, именно, в область мнимого. Аналогично тому как комплексные чисела являются расширением действительных. Для "ликбеза" полезно было показать элемент "Марку" как двойственный элементу для "Маркера", они двойственны как прямая и точка. Приведённые шесть модулей - это безусловно большая проделанная работа, похвально.
Хейфец Александр Львович (11 марта 2017 г. 17:16)	Виктор Анатольевич. О Вашем предложении включить программу построения коник в Компас. Аскон Вашу программу не берет, и вероятно не возмет, по двум причинам: В компасе нет AutoLispa, а кто будет переписывать программу на С++; В AutoCAD’e нет явного построения парабол и гипербол. В программе они  выполняются выходом в 3d пространство как сечения кругового конуса. Поэтому она в Компасе также не пойдет. Это вторая причина. В 2d части программы Вы только находите параметры этого сечения по алгоритму теоремы Паскаля. Или Вы строите эти коники как сплайны по точкам, тогда какова же точность. А.Л. Хейфец
Хейфец Александр Львович (15 марта 2017 г. 10:54)	Виктор Анатольевич, мои студенты успешно строят поверхности. заданные явно как z-f(x,y) и параметрически, где х(t), y(t) z(t) или заданы несколькими параметрами. Все в нашем учебнике: и красивые примеры,  и программы их построения, и давно известно.: Инженерная 3d комаьютерная графика. 3-е издание. 2015.. Разд. 25.3 А любоваться уравнениями - это болезнь. А.Л. Хейфец