ПОСТРОЕНИЕ ФУНДАМЕНТАЛЬНЫХ ТОЧЕК КВАДРАТИЧНОГО КРЕМОНОВА ПРЕОБРАЗОВАНИЯ, ЗАДАННОГО СЕМЬЮ ПАРАМИ СООТВЕТСТВЕННЫХ ТОЧЕК

Предлагается конструктивное решение задачи построения фундаментальных точек квадратичного бирационального преобразования, заданного семью парами со-ответственных точек. Для точного решения задачи используются средства компьютерного геометрического моделирования.

Введение

Развитие средств компьютерной графики приводит не только к появлению принципиально новых методов геометрического моделирования [1], но и предоставляет возможность конструктивного решения классических задач теоретической и прикладной геометрии. Одна из таких задач, связанная с теорией бирациональных (кремоновых) преобразований плоскости, была поставлена еще в 19 веке российским геометром К.А. Андреевым: требуется найти способ построения восьмой пары соответственных точек в квадратичном преобразовании, заданном семью парами точек. Решение сводится к построению двух корреляций, в которых искомая восьмая пара точек определяется с помощью линейного построения [2].

Обобщая задачу К.А. Андреева, приходим к проблеме поиска фундаментальных точек (F-точек) квадратичного преобразования, заданного семью парами соответственных точек. Почти полтора столетия обобщенная задача К.А. Андреева оставалась нерешенной. Формирование конструктивного алгоритма решения задачи и его практическая реализация стали возможны лишь с помощью средств компьютерного геометрического моделирования.

Постановка задачи

Квадратичное соответствие плоскостей П, П′ вполне определено семью парами точек. Требуется по семи парам соответственных точек A-A′, B-B′, C-C′, D-D′, E-E′, R-R′, T-T′ построить F-точки этого соответствия. Иначе говоря, в полях П, П′ надо найти три пары точек F₁-F′₁, F₂-F′₂, F₃-F′₃, из которых указанные семь пар точек проецируются тремя парами проективных пучков.

Выполним проективное преобразование плоскости П, переводящее четырехугольник ABCD в четырехугольник, конгруэнтный четырехугольнику A′B′C′D′ поля П′. Совместим плоскости П и П′ до совмещения  конгруэнтных четырехугольников. Получаем задачу: на совмещенной плоскости П=П′ требуется найти F-точки преобразования, заданного семью парами точек, из которых четыре пары точек совпадают.

Вспомогательная задача

Из трех пар не совпадающих соответственных точек выделим какие-либо две пары, например, E-E′, R-R′, не принимая во внимание оставшуюся пару T-T′. Сформулируем вспомогательную задачу: на совмещенной плоскости П=П′ надо найти F-точки квадратичного преобразования w_ER, заданного шестью парами соответственных точек A=A′, B=B′, C=C′, D=D′, E~E′, R~R′. 

Ассоциированные точки F₁, F′₁ преобразования w_ER определяются на пересечении прямых, соединяющих соответственные точки E~E′ и R~R′. Проективные пучки (F₁) и (F′₁) тождественны. Получаем центральное квадратичное преобразование с центром F₁=F′₁=EE′∩RR′. Произвольное коническое сечение, проходящее через совпадающие соответственные точки, представляет собой инвариантную конику преобразования w_ER. Через четыре точки можно провести пучок конических сечений Ф, поэтому существует однопараметрическое множество квадратичных преобразований, удовлетворяющих условиям вспомогательной задачи.

Выделяя произвольное коническое сечение k₁ пучка Ф, получаем центральное квадратичное преобразование (w_ER)₁, заданное центром F₁=F′₁=EE′∩RR′, инвариантной коникой k₁ и двумя парами соответственных точек E-E′, R-R′. Ассоциированные точки F₂, F′₂ этого преобразования принадлежат конике k₁. Действительно, соответственные лучи проективных пучков (F₂) и (F′₂) должны пересекаться в совпадающих соответственных точках на k₁, следовательно, вершины F₂, F′₂ этих пучков должны быть инцидентны k₁. Ассоциированные точки F₃, F′₃ преобразования (w_ER)₁ также инцидентны k₁.

Для построения точек F′₂, F′₃ отмечаем на k₁ произвольные точки K_i (i=1, 2, 3). Проецируя точки E, R из K_i на k₁, получаем на k₁ точечные ряды R_i и E_i, инволюционно соответственные ряду K_i. Ряды R_i, E_i проективны. Проецируя ряд E_i на конику k₁ из точки E′, получаем ряд E′_i, инволюционно соответственный ряду E_i. Проецируя ряд R_i из точки R′, получаем ряд R′_i, инволюционно соответственный ряду R_i. Ряды R_i и E_i проективны, следовательно, ряды R′_i и E′_i также проективны. Находим ось проективности f′₁ этих рядов и отмечаем точки F′₂, F′₃ пересечения оси f′₁ с коникой k₁. Эти точки являются двойными точками проективных рядов R′_i - E′_i и искомыми F′-точками преобразования (w_ER)₁ в плоскости П′. Точки F₂, F₃ преобразования (w_ER)₁ инцидентны исключенным прямым j′₂=F′₁F′₃ и j′₃=F′₁F′₂. Таким же образом определяются F-точки любого квадратичного преобразования, удовлетворяющего условиям вспомогательной задачи.

Конструктивный алгоритм построения F-точек

Совмещаем поля П, П′ до совпадения каких-либо четырех пар соответственных точек, например, A=A′, B=B′, C=C′, D=D′. Для обеспечения такого совмещенного положения полей требуется предварительно выполнить коллинеарное преобразование одного из полей.

Действие 1. Исключаем из рассмотрения какую-либо пару не совпадающих соответственных точек, например, T-T′. Рассматриваем однопараметрическое семейство квадратичных преобразований ω_ER, заданное четырьмя парами совпадающих соответственных точек и двумя парами не совпадающих соответственных точек E-E′, R-R′. Выделяя три произвольных конических сечения k₁, k₂, k₃=AC∩BD пучка Ф(ABCD), получаем три центральных квадратичных преобразования (w_ER)₁, (w_ER)₂, (w_ER)₃ с общим центром F₁=F′₁ и инвариантными кониками k₁, k₂, k₃ (рис. 1).

Решая вспомогательную задачу, на каждой конике k₁, k₂, k₃ находим две пары ассоциированных точек F₂~F′₂, F₃~F′₃, из которых все соответственные точки (кроме исключенной пары T~T′) проецируются двумя парами проективных пучков. Каждой конике k_i ставятся в соответствие две хорды: хорда f_i=F_2i -F_3i (в поле П) и хорда f′_i=F′_2i-F′_3i (в поле П′). Хорды f_i образуют пучок прямых с вершиной в точке Q_ER (рис. 1, а). Хорды f′_i также образуют пучок прямых с вершиной в точке Q′_ER (рис. 1, б). 

Лемма 1. Хорды f_i и f′_i образуют пучки прямых, проективные пучку конических сечений k_i. Доказательство леммы основано на теореме Паскаля и на свойствах проективных соответствий в образах второго порядка.

Таким образом, согласно лемме 1, пучки хорд (Q_ER) и (Q′_ER) проективны пучку коник Ф.

Действие 2. Исключаем из рассмотрения другую пару не совпадающих соответственных точек, например, R~R′. Получаем семейство квадратичных преобразований ω_ET, заданное шестью парами соответственных точек A=A′, B=B′, C=C′, D=D′, E~E′, T~T′. Выделяем из Ф те же самые коники k₁, k₂, k₃, что и в первом действии.

Решая вспомогательную задачу, на каждой конике находим две пары ассоциированных точек F₂~F′₂, F₃~F′₃, из которых все соответственные точки (кроме исключенной пары R~R′) проецируются двумя парами проективных пучков. Каждой конике k_i ставим в соответствие хорды f_i=F_2i–F_3i и f′_i=F′_2i–F′_3i. Получаем пучки хорд Q_ET(f₁, f₂, f₃,…) и Q′_ET(f′₁, f′₂, f′₃,…), проективные пучку коник Ф(k₁, k₂, k₃,…).

Действие 3. Исключаем соответственные точки E-E′. Рассматриваем семейство квадратичных преобразований w_RT, заданное шестью парами соответственных точек A=A′, B=B′, C=C′, D=D′, R-R′, T-T′. Из пучка Ф выделяем те же самые коники k₁, k₂, k₃, что и в предыдущих действиях. Решая вспомогательную задачу, на каждой конике находим две пары ассоциированных точек F₂-F′₂, F₃-F′₃, из которых все соответственные точки (кроме исключенной пары E-E′) проецируются двумя парами проективных пучков. В каждом из преобразований (w_RT)_i инвариантной конике k_i ставятся в соответствие хорды f_i=F_2i–F_3i и f′_i=F′_2i–F′_3i. Получаем пучки хорд Q_RT(f₁, f₂, f₃,…) и Q′_RT(f′₁, f′₂, f′₃,…), проективные пучку коник Ψ(k₁, k₂, k₃,…).

Примечание. Если в действиях 1…3 используются вырожденные коники пучка Ф, то построение F-точек и пучков хорд в преобразованиях w выполняется геометрически точно (“одной линейкой”).

Действие 4. Рассмотрим пару w-преобразований, например, w_ER и w_ET. Пучки хорд, порожденные этой парой преобразований,  проективны пучку коник Ф, следовательно, проективны между собой.

Точки G пересечения проективно соответственных хорд f_ER и f_ET определяют конику g_E, проходящую через точку E и через вершины Q_ER, Q_ET (рис. 2, а). Точки G′ пересечения соответственных хорд f′_ER и f′_ET определяют конику g′_E, проходящую через E′ и через вершины Q′_ER, Q′_ET (рис. 2, б).

Действие 5. Совместно рассмотрим другую пару преобразований, например, w_RT и w_ET. Пучки хорд (Q_RT) и (Q_ET), порожденные этими преобразованиями, проективны пучку коник Ф, следовательно, проективны между собой. Пучки (Q′_RT) и (Q′_ET) также проективны. Точки G пересечения проективно соответственных хорд f_RT и f_ET в пучках (Q_RT) и (Q_ET) определяют кривую второго порядка g_T, проходящую через вершины Q_RT, Q_ET и через точку T, общую в преобразованиях ω_RT и ω_ET. Точки G′ пересечения соответственных хорд f′_RT и f′_ET в пучках (Q′_RT) и (Q′_ET) определяют кривую второго порядка g′_T, инцидентную вершинам Q′_RT, Q′_ET и точке T′.

Примечание. В результате выполнения действий 4, 5 получены две пары вспомогательных кривых второго порядка g_E~g′_E и g_T~g′_T. Далее будет показано, что решение задачи поиска F-точек преобразования Ω сводится к построению точек пересечения g_E∩g_T, g′_E∩g′_T этих кривых. Задача построения точек пересечения кривых второго порядка не может быть решена геометрически точно (“линейкой и циркулем”).

Действие 6. Возвращаемся к рассмотрению исходного квадратичного преобразования, заданного семью парами соответственных точек, из которых четыре пары совпадают.

Лемма 2. Фундаментальные точки F₁, F₂, F₃ поля П совпадают с точками пересечения конических сечений g_E и g_T, а точки F′₁, F′₂, F′₃ поля П′ совпадают с точками пересечения коник g′_E и g′_T.

Доказательство леммы 2 основано на том обстоятельстве, что проективно соответственные лучи в пучках (F_i), (F′_i) определяют конику f_i, проходящую через базисные точки пучка Ф (рис. 3).

Таким образом, для окончательного решения поставленной задачи достаточно отметить точки пересечения g_E-g_T, g′_E-g′_T вспомогательных конических сечений. В соответствии с леммой 2, эти точки являются искомыми F-точками преобразования Ω на совмещенной плоскости П=П′.

Исследование

Вспомогательные кривые второго порядка g_E, g_T пересекаются в четырех точках. Чтобы выбрать из них искомые точки F₁, F₂, F₃, заметим, что коника g_E образована проективными пучками (Q_ET) и (Q_ER), а коника g_T – проективными пучками (Q_ET) и (Q_RT). Вспомогательные кривые g_E, g_T проходят через вершину Q_ET общего для обеих коник пучка (Q_ET). Следовательно, Q_ET – одна из четырех точек пересечения вспомогательных кривых. Оставшиеся три точки пересечения указывают искомые F-точки исследуемого квадратичного преобразования.

Вспомогательные кривые g′_E и g′_T также пересекаются в четырех точках, одна из которых совпадает с точкой Q′_ET . Оставшиеся три точки пересечения вспомогательных коник g′_E, g′_T указывают точки F′₁, F′₂, F′₃ исследуемого преобразования.

Чтобы из найденных F и F′ точек выделить ассоциированные пары, напомним, что ассоциированные пары F-точек располагаются на одной и той же конике пучка Ψ (см. рис. 3). Поэтому для выделения точки F′₁, ассоциированной с точкой F₁, достаточно начертить коническое сечение f₁, проходящее через F₁ и через базисные точки пучка Ф. Коника f₁ пройдет через искомую точку F′₁. Точно так же определяются две другие пары ассоциированных F-точек.

Две точки пересечения вспомогательных коник могут быть мнимыми. В этом случае получаем квадратичное преобразование с двумя парами мнимых сопряженных F-точек, которое может быть приведено (посредством специально подобранного проективного преобразования одного из полей П, П′) к преобразованию Гирста с центром внутри инвариантной коники. Преобразование Гирста с внутренней центральной точкой, в свою очередь, может быть сведено к инверсии относительно окружности.

Графический эксперимент

Искомые F-точки найдены на пересечении двух пар вспомогательных коник g_E-g′_E и g_T-g′_T. Конические сечения g_E и g′_E образованы проективными пучками, порожденными преобразованиями w_ER и w_ET (см. действие 4). Коники g_T и g′_T образованы проективными пучками (Q_RT) и (Q_ET), порожденными преобразованиями w_RT и w_ET (см. действие 5). Для проверки решения найдем еще одно вспомогательное коническое сечение g_R, образованное проективными пучками хорд (Q_RT) и (Q_ER) в преобразованиях w_RT и w_ER. Коническое сечение g_R проходит через точку R, через вершины проективных пучков Q_RT, Q_ER и через ранее найденные F-точки, что подтверждает достоверность разработанного алгоритма и правильность найденного решения (рис. 4). Особо отметим замечательную конструктивную точность найденного решения: три конических сечения четко (с точностью “до привязок”) пересекаются в искомых точках!

Заключение

Предложен алгоритм построения фундаментальных точек квадратичного бирационального (кремонова) преобразования, заданного семью парами соответственных точек. Для реализации алгоритма требуется вычерчивать вспомогательные кривые второго порядка и отмечать точки их пересечения. Эти операции выполняются с помощью компьютерной программы “Универсальный коникограф” [4, 5]. Отличительная особенность программы состоит в том, что она выполняет геометрически точное построение не кривой второго порядка, а ее метрики – главных осей, фокусов и асимптот.  Только после определения метрики вычерчивается непрерывная кривая. Очевидно, если известна метрика (главные оси и др.) кривой второго порядка, то последующее ее вычерчивание не вызывает затруднений и может быть выполнено на компьютере с любой заранее заданной степенью точности. В качестве исходных данных для определения метрики конического сечения может быть задан любой внутренне непротиворечивый набор точек и касательных, в том числе – мнимых [6].  

Практическая значимость предложенного алгоритма связана с принципиальным свойством кремонова преобразования: образом рациональной кривой является рациональная кривая. Рациональные кривые наилучшим образом подходят для конструирования технических форм, так как в силу рациональности расчет их локальных геометрических характеристик осуществляется наиболее просто. В связи с этим кремоновы преобразования широко применяются для конструирования рациональных кривых с заданными динамическими свойствами [3]. Полученный в статье результат служит развитию теории кремоновых преобразований и применению их в практике геометрического компьютерного моделирования.

Список литературы

1. Толок, А.В. Функционально-воксельный метод в компьютерном моделировании: монография / А.В. Толок. – М.: Физматлит, 2016. – 112 с.

2. Андреев, К.А. О геометрических соответствиях в применении к вопросу о построении кривых линий / К.А. Андреев – М.: Издание Московского Математического общества, состоящего при Императорском Московском Университете, 1879. – 168 с.

3. Иванов, Г.С. Конструирование технических поверхностей: монография / Г.С. Иванов. – М.: Машиностроение, 1987. – 192 с.

4. Короткий, В.А. Универсальный компьютерный коникограф / В.А. Короткий, Л.И. Хмарова // Труды 26-й Международной научной конференции GraphiCon 2016 (19-23 сентября 2016), ННГАСУ, Нижний Новгород, Россия. – С. 347-351.

5. Свидетельство о государственной регистрации № 2011611961 от 04.03.2011. Построение кривой второго порядка, проходящей через данные точки и касающейся данных прямых (программа для ЭВМ) / Короткий В.А.

6. Короткий, В.А. Графические алгоритмы реконструкции кривой второго порядка, заданной мнимыми элементами / А.Г. Гирш, В.А. Короткий // Геометрия и графика. 2016. Т. 4. № 4. С. 19-30. DOI: 10.12737/22840.

Рисунки к докладу

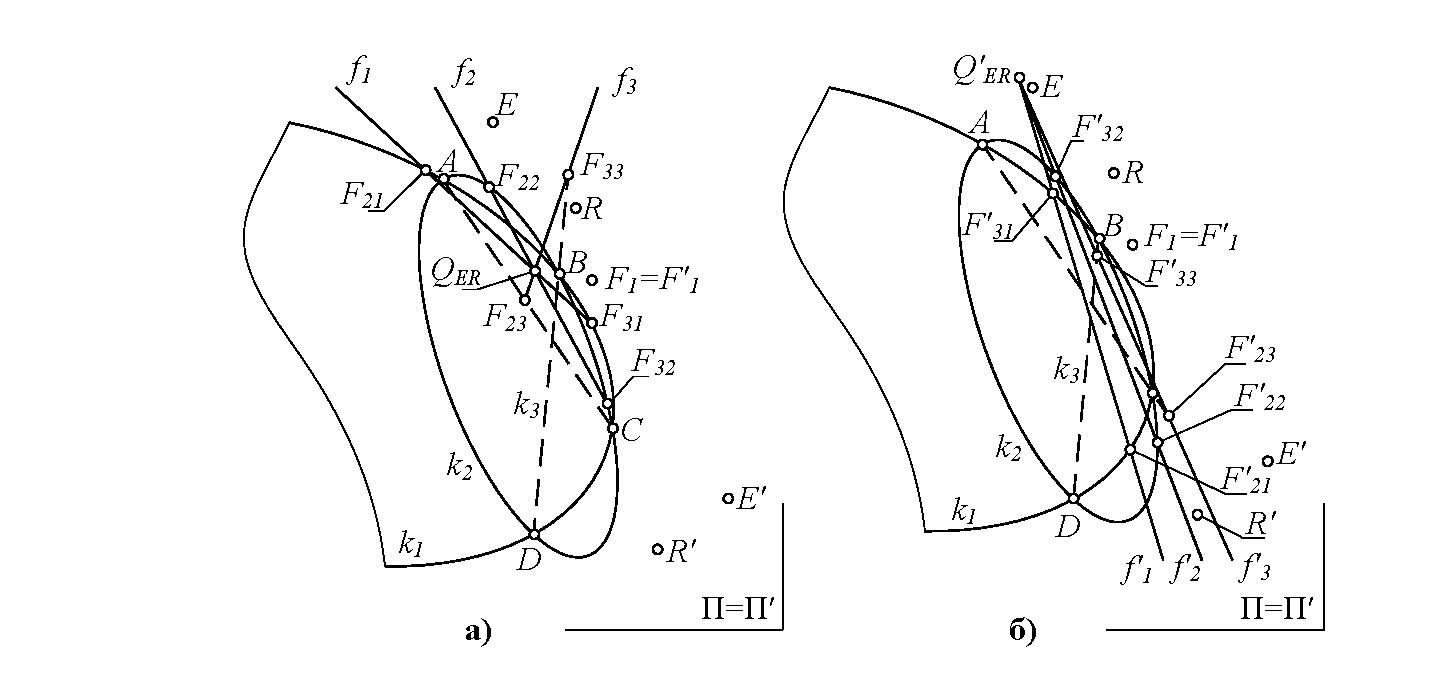
Пучки хорд преобразования w_ER: а – хорды f_i=F_2i-F_3i; б – хорды f′_i=F′_2i-F′_3i (i=1,2,3)  

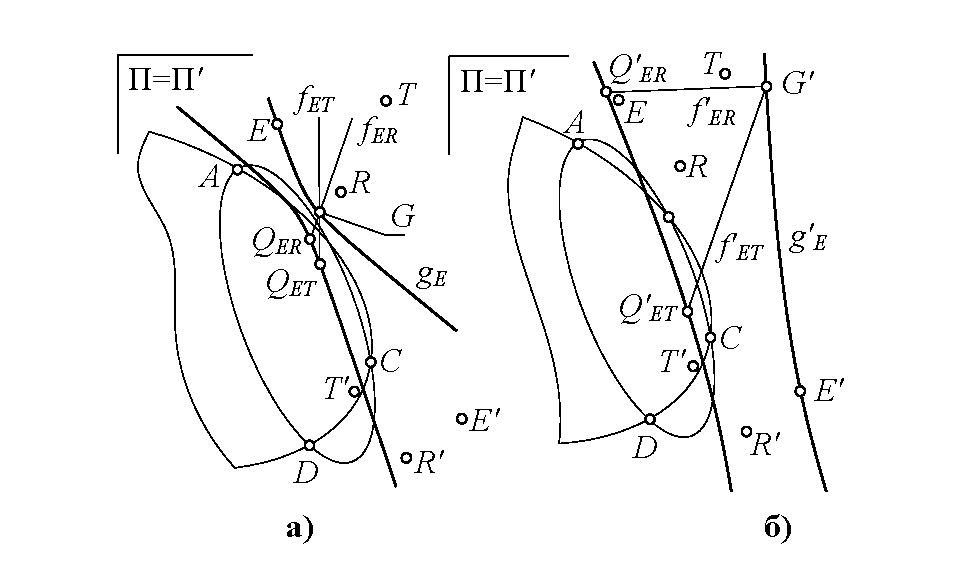
Коники, образованные проективными пучками хорд в преобразованиях w_ER и w_ET: а – коника g_E в поле П; б – коника g′_E в поле П′  

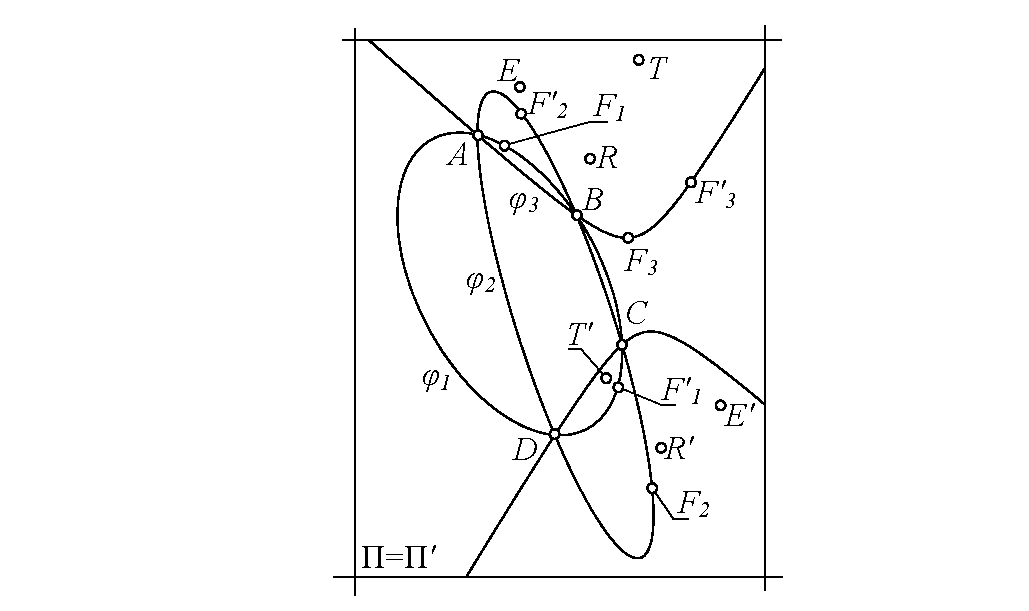
Коники f₁...f₃

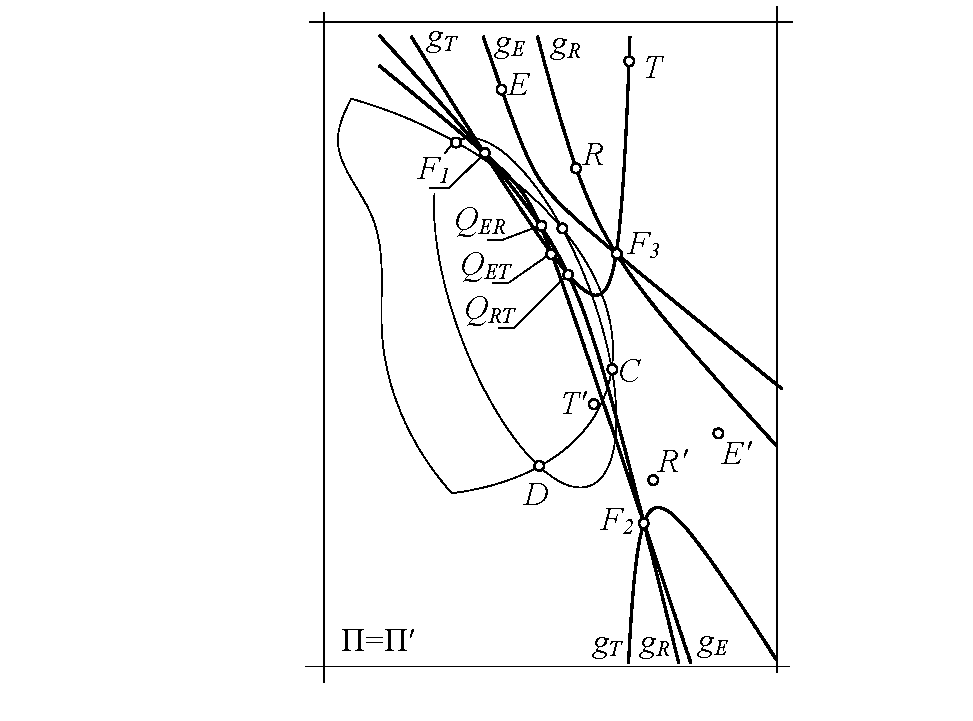
Проверка решения

Гирш Антон Георгиевич (7 марта 2017 г. 16:25)	Виктор Анатольевич, поздравляю. Достойая тема, хорошая заявка доклада. Уровень выше среднего - не сразу настроишся вникнуть.