СВОЙСТВА ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ С ОБЩЕЙ ПЛОСКОСТЬЮ СИММЕТРИИ

В данной статье рассматриваются задачи на построение линии пересечения алгебраических поверхностей с общей плоскостью симметрии (кроме случаев распадения линии на две плоские кривые) в система трехмерного твердотельного моделирования КОМПАС-3D.

Технические возможности компьютерной графики позволяют перейти на новый уровень преподавания графических дисциплин. Использование компьютерной техники дает возможность сократить время, отводимое на отработку некоторых тем начертательной геометрии, повысить эффективность усвоения предмета благодаря хорошей наглядности изучаемого материала, обеспечить развитие пространственно-образного мышления и приобрести новые навыки и приемы работы с системой компьютерной графики.

В учебных целях для обучения студентов машиностроительных специальностей на кафедре инженерной и компьютерной графики наряду с другими графическими системами используется система трехмерного твердотельного моделирования КОМПАС-3D, разработанная российской компанией «АСКОН». Использование методов создания трехмерных моделей сокращает трудоемкость решения задач начертательной геометрии на построение линии пересечения поверхностей, увеличивает наглядность пересекающихся геометрических тел, позволяет анализировать характер линии в зависимости от параметров пересекающихся объектов.

В настоящей работе рассматриваются задачи на построение линии пересечения алгебраических поверхностей с общей плоскостью симметрии (кроме случаев распадения линии на две плоские кривые).

Рассматриваются следующие этапы при решении данных задач:

1. Создается трехмерная модель пересекающихся геометрических тел
2.  На основе модели формируется чертеж объектов с автоматически построенной линией пересечения. Ассоциативная связь чертежа с моделью позволяет анализировать линию при изменении параметров пересекающихся объектов;
3. Определяется вид линии на фронтальной проекции, ее характерные точки, асимптоты, фокусы и т.д.

В основе решения подобных задач лежит следующая теорема:

Если две пересекающиеся алгебраические поверхности 2-го порядка имеют общую плоскость симметрии, то линия их пересечения проецируется на эту или другую ей параллельную плоскость в виде кривой 2-го порядка.

Эту теорему можно доказать аналитически на примере пересечения двух цилиндров вращения (рис. 1), [1].

Пусть в системе координат OXYZ  пересекаются цилиндры Ф и Г  (рис. 1), оси которых совпадают с осями координат X и Z. Тогда плоскость XOZ , будет общей плоскостью симметрии заданных поверхностей.

В выбранной системе координат цилиндр Ф описывается уравнением

x²  + y² = R₁² ,

 а цилиндр Г — уравнением

z²  + y² = R₂² .

Тогда система уравнений

x²  + y² = R₁²

z²  + y² = R₂²

описывает пространственную кривую m четвертого порядка, образовавшуюся в результате пересечения двух заданных цилиндров.

Установим уравнение проекции m₂  кривой m пересечения на плоскость П₂ , параллельную общей плоскости симметрии XOZ. Для этого исключим из системы уравнений координату y.

y ² =R₁² – x²

z ²+ R₁²  – x²  = R₂²

z ²  – x²  = R₂²  – R₁²

Откуда    

z² /(R₂²  – R₁² ) – x² /(R₂²  – R₁² ) = 1.

Полученное уравнение описывает равностороннюю гиперболу ― плоскую кривую второго порядка.

В соответствии с изложенным,  линии пересечения поверхностей второго порядка, имеющие общую плоскость симметрии, будут проецироваться в кривые второго порядка ― гиперболы, параболы, эллипсы. Вид проекции кривой определяется видом пересекающихся поверхностей. Наиболее часто встречающиеся случаи пересечения данных поверхностей представлены на рис. 2 [1].

Так, в гиперболу проецируется линия пересечения конусов, цилиндров, параболоидов и растянутых эллипсоидов.

В параболу проецируется линия пересечения сферы с конусом, цилиндром, параболоидом, гиперболоидом, эллипсоидом.

В эллипс проецируется линия пересечения сжатого эллипсоида с цилиндром, конусом, параболоидом, гиперболоидом, растянутым эллипсоидом.

Перечисленные типы линий автоматически создаются на ассоциативных видах в документе Чертеж в результате формирования моделей геометрических тел в режиме  Деталь.

На ниже представленных примерах рассмотрим, как на полученных линиях определить ее элементы ― отдельные точки, оси, вершины, асимптоты, фокусы .

Пример 1. Пересечение конуса и цилиндра, оси которых пересекаются не под прямым углом (рис. 3).

Для нахождения положения асимптот гиперболы в конус вписывают сферу с центром в точке пересечения осей конуса и цилиндра, а затем цилиндр растягивают до касательного к построенной сфере. Точки пересечения очерковых образующих конуса и растянутого цилиндра соединяют прямыми, которые пересекаясь не под прямым углом, будут асимптотами неравносторонней гиперболы. Через точку пересечения асимптот проводим действительную ось гиперболы, которая является биссектрисой угла между асимптотами. Вершинами гиперболы A и B являются точки пересечения действительной оси с кривой. Перпендикулярно к действительной оси проводим мнимую ось.

Пример 2. Пересечение двух конусов, оси которых пересекаются под прямым углом (рис.4).

Вершины гиперболы A и B находим с помощью сферы, вписанной в конус с наибольшим углом при вершине. Делим отрезок АВ пополам и находим центр гиперболы ― точку О₁.

Для нахождения асимптот гиперболы соосно с конусом, имеющим меньший угол при вершине, строим конус, касательный к вписанной сфере. Точки пересечения очерковых образующих заданного и построенного конусов соединяем прямыми линиями. Через центр О₁ проводим линии им параллельные, которые и будут являться асимптотами гиперболы.

Список литературы

1. Дубров А. А. и др. Метод. указания. Построение линии пересечения поверхностей вращения с общей плоскостью симметрии. Харьков, ХИРЭ, 1982.    

Рисунки к докладу

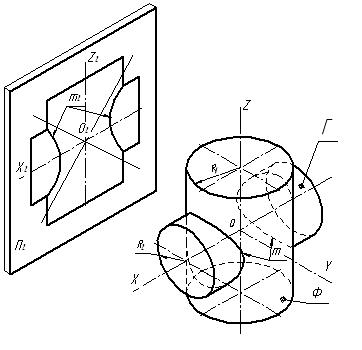
Пересечение двух цилиндров вращения

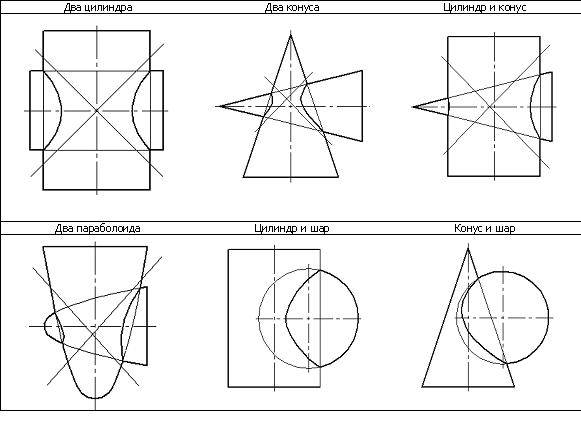
Варианты пересечения поверхностей

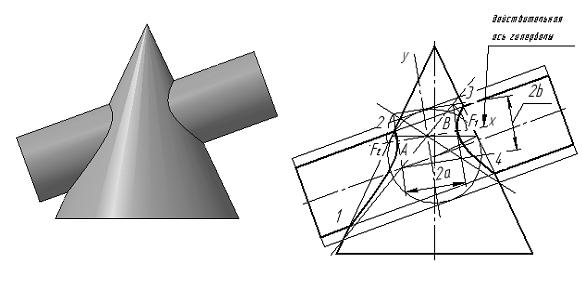
Пересечение конуса и цилиндра

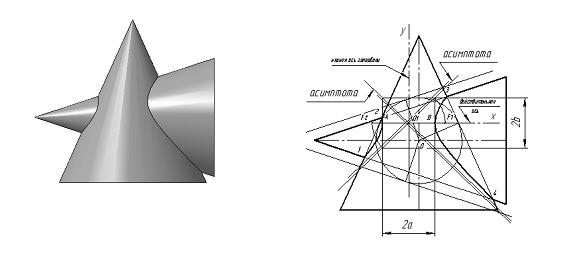
Пересечение двух конусов под прямым углом

Дударь Елена Сергеевна (12 марта 2017 г. 11:23)	Добрый день, Эдуард Владимирович,  Любовь Александровна и Надежда Васильевна! Спасибо, что делитесь с нами конкретным опытом, так подробно и обстоятельно.  В вашем докладе мне показалось интересным сочетание основ геометрии, твердотельного моделирования и аналитического решения задачи. Применяется ли изложенная методика анализа искомой линии пересечения при выполнении лабораторных работ и сколько часов на это отводится?    С уважением, Елена С. Дударь
Иванов Геннадий Сергеевич (12 марта 2017 г. 20:29)	Уважаемые Эдуард Владимирович, Любовь Александровна, Надежда Васильевна! Содержание Вашей статьи выпукло отражает состояние и противоречия в преподавании начертательной геометрии в настоящее время. С одной стороны, имеем заметное снижение научно-методического уровня ее преподавания. (моя трудовая деятельность на кафедре графики началась в 1962 - ом году – после окончания института, поэтому мой опыт и стаж позволяют судить об этом профессионально). В частности, рецензируемая статья по своему научному уровню далека от аналогичной статьи Е.А. Глазунова «О проекции линии пересечения двух поверхностей второго порядка, имеющих общую плоскость симметрии» /Труды Московского семинара по начертательной геометрии и инженерной графике, М., Советская наука, 1958. С. 35 - 69. С другой стороны, надеяться на повышение уровня знаний студентов простым (механическим) использованием компьютеров в решении задач НГ без соответствующего геометрического обеспечения, не приходится. Например, пусть рассматриваемые в статье поверхности имеют точку касания. Она на линии их пересечения может быть узловой, возврата и изолированной. Если на изображении узловую точку и точку возврата можно отличить, то как быть с изолированной точкой? Еще один, с моей точки зрения, убедительный пример: даны две конические поверхности второго порядка с общей вершиной, их направляющие a и b принадлежат одной плоскости. Четыре их точки пересечения могут быть действительными и различными, мнимыми и совпадать в различных комбинациях! Соответственными будут вид и взаимное положение образующих, по которым пересекаются эти конические поверхности. Как быть в этом случае? Эта простая на первый взгляд задача имеет прикладное значение: двумерный гладкий обвод из отсеков рассматриваемых конических поверхностей с двумя, тремя и четырьмя совпавшими образующими можно использовать наподобие известных поверхностей Кунса для аппроксимации технических форм различного назначения. С этим же вопросом перекликаются статьи А.Г. Гирша, В.А. Короткого, опубликованные в материалах этой конференции. Эти противоречия не являются непреодолимыми: они лишь отражают проявление «болезни роста». В идеале проблема заключается в обеспечении максимально возможного вклада начертательной (инженерной) геометрии для достижения необходимого уровня геометрической подготовки студентов с целью успешного освоения материалов последующих курсов, начиная от смежных разделов высшей математики и заканчивая курсом математического моделирования для магистров. С уважением Г.С. Иванов
Козырев Эдуард Владимирович (16 марта 2017 г. 10:34)	Уважаемый Геннадий Сергеевич ! Я боагодарен Вам за комментарий к моей статье. Прочитал Ваши замечания с большим интересом.В ответ хочу сказать, что данная статья не является научной. Она ориентирована на студентов первого курса. Хотелось показать связь аналитической геометрии с её уравнениями поверхностей и начертательной геометрии с её графическими приёмами построения линии пересечения. Для большей наглядности привлечена компьютерная графика, которую студенты только начинают изучать. Материал статьи несёт учебный характер и используется в кружковой работе со студентами.   С уважением, Э.В.Козырев.
Козырев Эдуард Владимирович (16 марта 2017 г. 10:42)	Уважаемая Елена Сергеевна ! Спасибо за благожелательный комментарий к статье. На тему "Взаимное пересечение поверхностей" выделяется 2 практических занятия. Первое - построение линии пересечения поверхностей методами вспомогательных секущих плоскостей и сфер. Студенты вручную выполняют графическую работу на формате А3. Второе занятие - моделирование пересекающихся объектов (лабораторная работа по компьютерной графике) с анализом линии в зависимости от размеров одного из объектов. Если на занятиях появляется свободное время, то рассматриваются параметры линии и её характерные точки. Материал статьи предназначен для кружковой работы со студентами.   С уважением, Э.В.Козырев.
Селиверстов Александр Владиславович (16 марта 2017 г. 11:33)	Здравствуйте, Эдуард Владимирович, Любовь Александровна и Надежда Васильевна! Расскажите немного подробнее об организации кружковой работы. Какая доля от всех студентов первого курса участвует в работе кружка? Учитываются ли успехи студентов? С уважением, А.В. Селиверстов
Козырев Эдуард Владимирович (22 марта 2017 г. 13:02)	Здравствуйте, Александр Владиславович! Об организации кружковой работы со студентами ничего оригинального сообщить не могу. У меня в так называемом "кружке" участвуют три -- два человека, обычно по два человека на одну тему. Приглашаются успевающие студенты с обещанием сократить обязательную графическую работу и повышением оценки на зачете. Студентам предлагается уже готовая работа, в которой ему следует разобраться. Далее он выступает с докладом на ежегодной кафедральной студенческой конференции. С целью повышения рейтинга преподавателя, включаю одного -- двух студентов в число авторов совместной статьи. С важением, Э.В. Козырев.