В статье рассматривается способ построения теоретической поверхности крыла летательного аппарата. Показана возможность решения классической задачи получения профиля Жуковского с применением методов проективной геометрии в САПР
Ключевые слова: Геометрическое моделирование, Аэрогидродинамика, САПР
В геометрическом моделировании вопросы, связанные с конструированием сложных технических привели к развитию группы методов, которые принято называть «Поверхностным моделированием», отличая их от методов «твердотельного моделирования». При этом, в разработке математического обеспечения систем геометрического моделирование, основное внимание уделяется средствам построения поверхностей и операциям над ними, обеспечивающими, прежде всего, выполнение требований конструктивного и технологического характера.
Так например, «корпуса судов, фюзеляжи и крылья самолетов часто проектируются с помощью поперечных или продольных сечений, проходящих в заданных местах. Эти сечения соединяются плавными кривыми, в результате чего получается единая трехмерная форма… а поверхности, построенные таким способом, называются сплайновыми поверхностями» [1].
Но конструктор, выбирая крыло, оценивает его с двух точек зрения. Во-первых, оно должно удовлетворять всем аэродинамическим требованиям, т. е. должно иметь определенную подъемную силу ...; во-вторых, оно должно иметь такую форму, которая позволила бы конструктивно его выполнить и притом с достаточным запасом прочности [2].
Средства моделирования, учитывающие теоретические принципы формообразования сложных технических поверхностей, являются узкоспециализированным ПО, не входящим в арсенал средств машиностроительных САПР общего назначения.
В случае необходимости автоматизации расчетных процедур применяются системы математического программирования либо прикладные интерфейсы программирования САПР, позволяющие получить требуемые геометрические параметры аналитическими методами.
Методы математического моделирования теоретических поверхностей изучаются в рамках различных прикладных областей: гидроаэродинамики, теории механизмов, оптики и др.
В эпоху становления этих инженерных дисциплин, на ряду с аналитическими, широкое применение имели геометрические методы. В исследованиях основоположника аэрогидродинамики Н.Е. Жуковского, геометрические методы играли совершенно исключительную роль: «Можно говорить, что математическая истина только тогда должна считаться вполне обработанной, когда она может быть объяснена каждому из публики, желающему ее усвоить. Я думаю, что, если возможно приближение к этому идеалу, то только со стороны геометрического толкования или моделирования» [3].
Теоретические профили, обладающие превосходными летными качествами, были введены в аэродинамику Н.Е. Жуковским и С.А. Чаплыгиным с учетом действия потока обтекающего крыло, представляют собой инверсии конических сечений в комплексной плоскости.
Для вычерчивания профилей Жуковского при заданных параметрах можно применить простой прием, указанный Треффтцем [4]. В специальной литературе можно найти описание множества вариаций данного метода [5]. Для этого достаточно применения традиционных геометрических инструментов - линейки и циркуля. Соответственно, с этой задачей может справиться и САПР. Но с ростом требований к точности построения растет и трудоемкость задачи. Т.н. «графическая сложность» синтетических процедур, в немалой степени, ограничила круг их применения, а в эпоху развития компьютерной графики и геометрического моделирования эти методы практически полностью уступили место аналитическим.
Но есть и другая точка зрения на эту проблему: «Необходимость перевода геометрической модели в аналитический вид может объясняться лишь недостатком теоретических, программных и методических разработок в области автоматизации процессов геометрического моделирования» [6].
Интереснейшим примером такой разработки, является система геометрического моделирования Симплекс. А задача построения профиля Жуковского по способу Треффтца позволяет наглядно продемонстрировать практические возможности системы.
В качестве прообразов для построения профиля возьмём множество точек расположенных на окружности. Для этого выполним вспомогательные построения: разместим точку p0 в начале координат и окружность d1 единичного радиуса с центром в некоторой окрестности начала координат. Затем через точку p0 проведем прямую o1 под углом α к оси oх. Величину α зададим через интервальный ряд содержащий n значений в диапазоне от 0 до 360. Таким образом, величина n будет определять множество прямых o1n. При создании геометрической модели удобно работать с небольшим количеством построений. Величина n=3 даст три экземпляра прямой o1, повернутых вокруг начала координат через одинаковые интервалы.
Каждая прямая множества o1n пересекает окружность d1 в двух точках. Для решения задачи по получению прообразов, изображенной на рис. 1, достаточно ограничиться только одним пересечением, что даст множество точек p1n,.
Построим окружность инверсии d2 касательную к d1 в некоторой точке таким образом, чтобы первая охватывала вторую.
В Симлекс, построение касающихся окружностей, как и описанные ниже инверсия и симметрия, реализованы в виде системных функций. Поэтому в статье не приводятся полные решения этих тривиальных геометрических задач. Но особое внимание хочется обратить на то, что любое построение, созданное в системе, может быть выделено пользователем в обособленный алгоритм, путем определения входных и выходных параметров, что обеспечивает возможность его повторного вызова в виде системной функции при решении новых задач. Данное решение, по сути, представляет собой оригинальный и весьма удачный способ применения широко распространённой в параметрических САПР технологии геометрического решателя (Geometric Solver).
Применение к построенным ранее прообразам p1n конформного отображения, лежащего в основе, так называемой функции Жуковского, геометрическая интерпретация которого представляет собой композицию инверсии относительно окружности и симметрии относительно оси ox, даст точки x1 и x2 соответственно (см. рис. 2).
Т.к. преобразование Жуковского является функцией комплексного переменного, которая конформно отображает область задания функции на область ее значений, то для получения окончательного результата применяются геометрические методы теории функций комплексного переменного. Точки x2n рассматриваются как геометрические образы комплексного числа, заданные на плоскости декартовыми координатами. Определим величину r, задаваемую расстоянием между точками p0 и х2, как модуль комплексного числа. В качестве аргумента используем величину α, т.к. углы между множеством отрезков заданных точками p0 и х2 и осью ох отличаются от α только некоторым смещением, не оказывающим принципиального влияния на результат. При отображении точек х2n относительно точек p1n, с использованием величины r в качестве расстояния, а α в качестве направления получим искомые образы составляющие профиль Жуковского – точки pn. Линию профиля получим путем аппроксимации точек pn сплайном.
Меняя величину n получаем необходимое количество точек, для которых решается задача. Отношение радиусов окружностей d1 и d2 определяет толщину профиля. Положение точки соприкосновения окружностей определяет изгиб профиля.
В задаче построения профиля можно избежать привлечения аппарата ТФКП, решая ее чисто конструктивно, но учитывая мнимые образы.
Система Симлекс содержит инструменты, позволяющие автоматически отображать мнимые образы, входящие в решение задачи, в расширенную комплексную плоскость. Для их учета в задаче построения профиля, нужно разместить точку p0 в мнимой области. На рис. 3, можно видеть, что часть точек в левой части комплексной плоскости соответствуют профилю Жуковского. Дополнительными параметрами, управляющими геометрией профиля становятся комлексные образы точки p0, смещение которых позволяет изменять например положение наиболее толстого участка профиля относительно кромок. Определяя управляющие параметры как интервальные можно получать различные семейства кривых.
Система Симплекс позволяет обмениваться данными с другими САПР в распространенных форматах. На рис. 5 изображена 3D-модель поверхности крыла, построенная в САПР КОМПАС-3D по точкам теоретического профиля, "расчитанным" в Симплекс.
Список литературы
- Голованов Н.Н. Геометрическое моделирование. —М., Издательство Физико-математической литературы, 2002, —472 с.
- Оглоблин А.П. Систематические исследования крыльев, Труды Центрального аэрогидродинамического института им. проф. Н. Е. Жуковского, выпуск 147 —М., НКТП СССР Главное управление авиационной промышленности, 1933, с. 32.
- Жуковский Н.Е. Избранные сочинения, том 1. —М.-Л., Государственное издательство технико-теоретической литературы, 1948, — 340 с.
- Кочин Николай Евграфович, Кибелъ Илья Афанасьевич, Розе Николай Владимирович Теоретическая гидромеханика, ч. 1 М., Физматгиз, 1963 г., —584 с.
- Коростелев Б.В. Инверсии кривых второго порядка как контуры аэродинамических профилей, Труды Центрального аэрогидродинамического института им. проф. Н. Е. Жуковского, выпуск 181 —М., НКТП СССР Главное управление авиационной промышленности, 1934, с. 72.
- Волошинов Д.В. Теория автоматизации проектирования объектов и процессов на основе методов конструктивного геометрического моделирования, Диссертация на соискание ученой степени доктора технических наук. —СПб., 2010, с. 363.
Рисунки к докладу
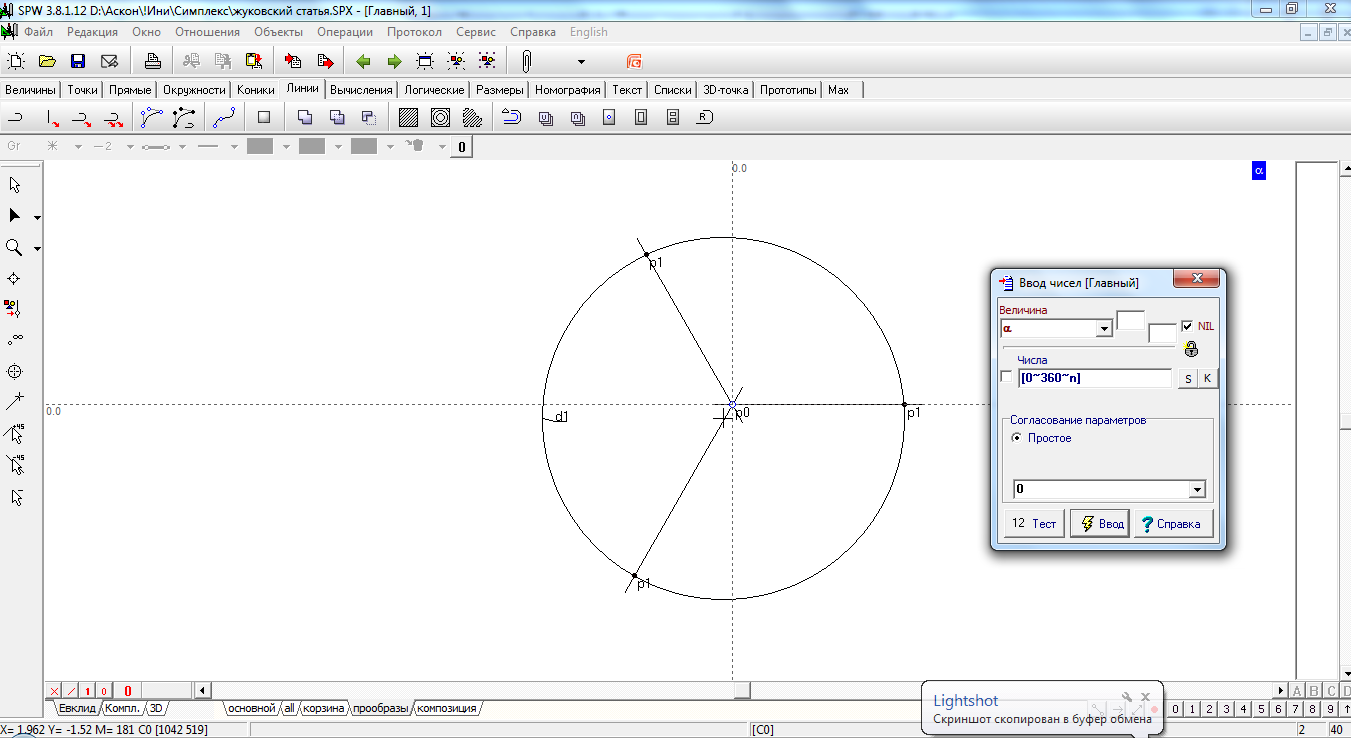
Рис. 1
Множество точек p2 - прообразы, необходимые для построения профиля Жуковского
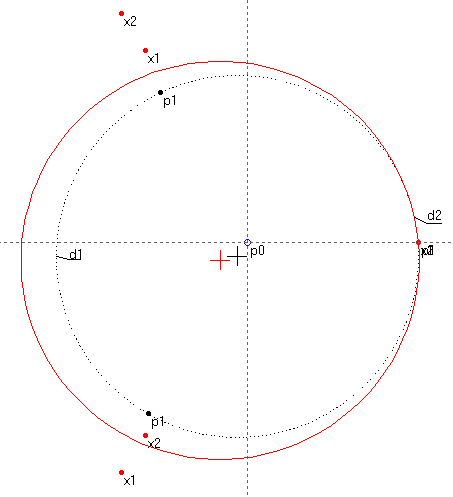
Рис. 2
Точки х1 и х2 результат конформного отображения прообразов
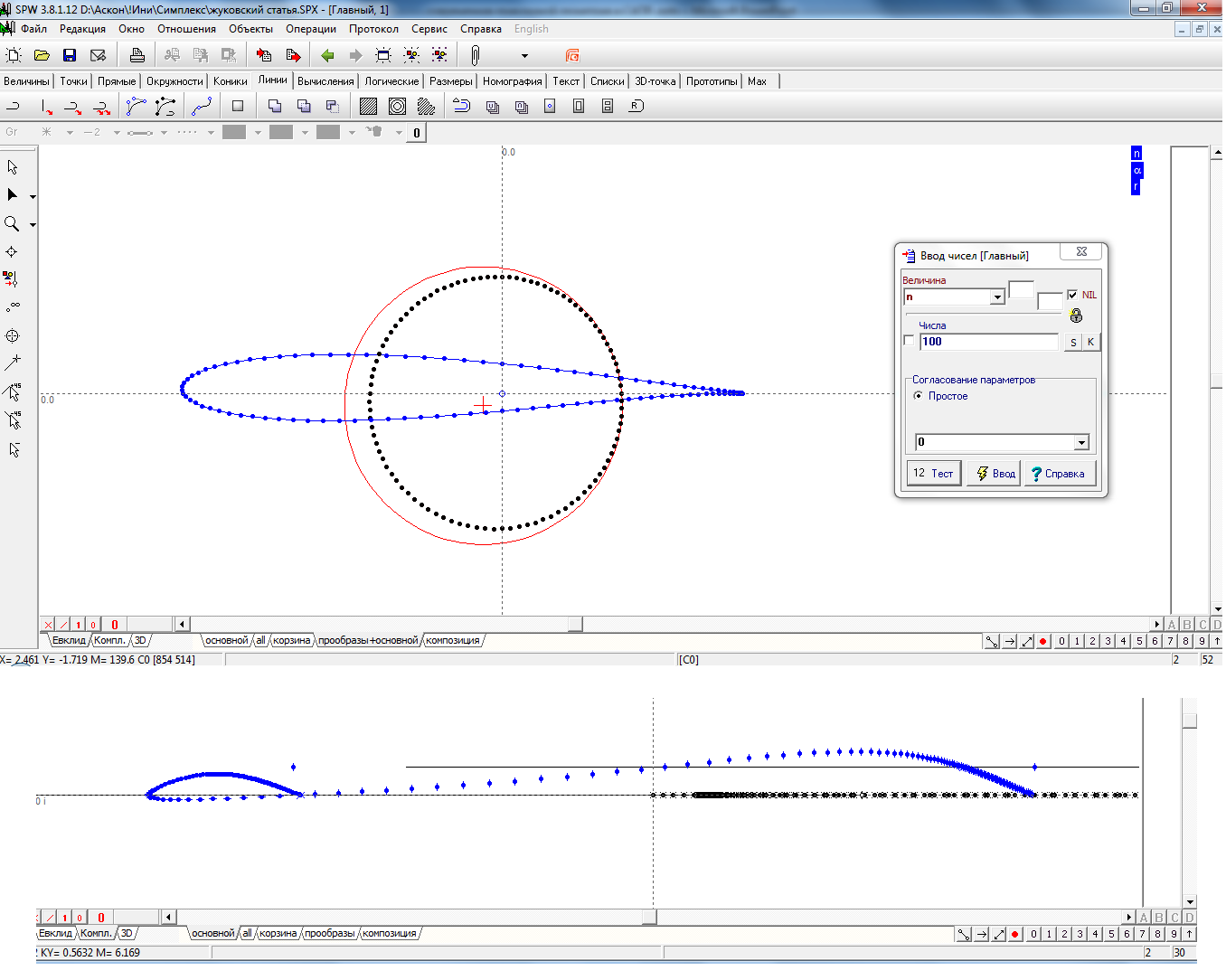
Рис. 3
Линия профиля Жуковского, построенная по 100 точкам на евклидовой и комплексной плоскостях
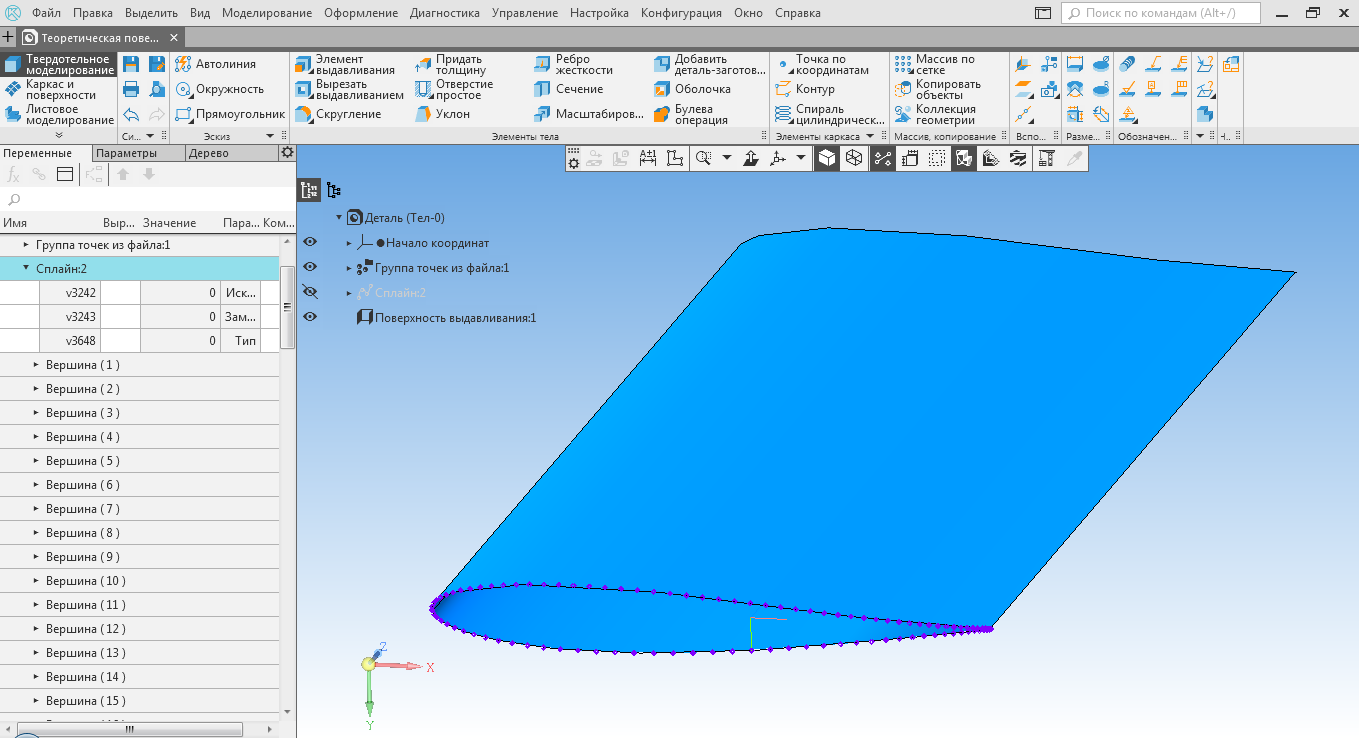
Рис. 4
3D-модель поверхности крыла, построенная в САПР КОМПАС-3D по точкам теоретического профиля, "рассчитанным" в Симплекс
Вопросы и комментарии к выступлению:

Тихонов-Бугров Дмитрий Евгеньевич (10 марта 2017 г. 16:28) |
Здравствуйте, уважаемый Пётр Владимирович. Наверное рис.5 нельзя называть моделью крыла т.к. она получена клонированием единственного профиля. Как известно, инженерный способ задания линейчатого каркаса крыла подразумевает наличие двух направляющих, далее процентная разбивка хорд... Как при построении реальной модели предполагается учитывать переменный характер формы профиля и траектории его премещения. Тихонов-Бугров. |
|
Никифоров Петр Владимирович (10 марта 2017 г. 21:12) |
Спасибо за замечание, Дмитрий Евгеньевич. Название у рисунка неудачное. Конечно крыло современного летательно аппарата это сложное изделие. Представленная на рисунке модель на это "не тянет". Основной целью была демонстрация возможностей применения Симплекс совместно с системами 3D-моделирования при решении практических задач.
|

Тихонов-Бугров Дмитрий Евгеньевич (11 марта 2017 г. 1:59) |
Пётр Владимирович, не следует ли из Вашего доклада, что компания АСКОН намерена использовать Симплекс в своих разработках? С уважением, Тихонов-Бугров. |

Короткий Виктор Анатольевич (11 марта 2017 г. 10:14) |
Уважаемый Петр Владимирович! Несколько лет назад я обращался к руководству фирмы Аскон с абсолютно некоммерческим предложением: сделать в Компасе кнопку “Построение КВП по любому набору точек и касательных”. При нажатии на эту кнопку выпадает меню из нескольких опций: “По пяти абсолютно произвольно указанным прямо на экране точкам (или точкам, заданным своими координатами) построить КВП”, “По 5 касательным построить КВП”, “По четырем точкам и касательной построить КВП”, “По 4 касательным построить параболу” … И так далее. Таких сочетаний очень много, но практически нужны всего несколько. Из Аскона пришел ответ – такая кнопка в Компасе ПОКА НЕ НУЖНА. Я Вас хотел попросить – узнайте, может быть, ситуация изменилась? Ведь неплохая кнопка будет, правда? Поясню подробнее. Программа, вернее, пакет нескольких программ, у меня есть, но на Лисп, в Автокаде. Они очень простые и имеют очень малый объем. Десятка три килобайт. Они снабжены подробнейшими комментариями к каждому оператору. Я могу это просто передать фирме Аскон. Но этого будет недостаточно, потому что комментарии были мной написаны только для себя и имеют личностный оттенок. Поэтому не всегда понятно. Например:…”перетащим эту чертову инволюцию на окружность”. Это легко перевести на литературный язык, но недостаточно для понимания сути геометрической операции. Требуется знание терминов проективной геометрии, поскольку алгоритмы имеют ИСКЛЮЧИТЕЛЬНО ПРОЕКТИВНЫЙ ХАРАКТЕР. Никакого 3D!!! Все построения выполняются исключительно на плоскости! Еще подробнее. Для построения метрики используются только два примитива – окружность и прямая, вследствие чего метрика КВП (центр, оси, асимптоты, фокусы) определяется МАКСИМАЛЬНО ТОЧНО. То есть НАИБОЛЕЕ ТОЧНО ПО СРАВНЕНИЮ С ЛЮБЫМ ДРУГИМ ВАРИАНТОМ. Это построение безусловно точнее и проще любого эквивалентного алгебраического алгоритма, в том числе – разнообразных параметризаций, встроенных в скрытые от нас системные файлы Автокада, Солида и др. Итак, и вопрос, и просьба. Вопрос. Как Вы считаете - нужна ли в Компасе кнопка, делающая кривую второго порядка, заданную любым набором точек и касательных, столь же простым и безупречно точно вычерчиваемым графическим примитивом, как прямая линия и окружность? И просьба. Если у Вас есть такая возможность – пожалуйста, предложите это руководству. Никакой коммерции, никакого маркетинга!! Только дружеское абсолютно безвозмездное сотрудничество. Любые дополнительные комментарии – по адресу OSPOLINA@MAIL.RU. С уважением, Короткий Виктор Анатольевич, Челябинск, ЮУрГУ.
|
|
Никифоров Петр Владимирович (11 марта 2017 г. 19:04) |
Дмитрий Евгеньевич, я не уполномочен говорить здесь от лица АСКОН. Но работаю в этой компании |
|
Никифоров Петр Владимирович (12 марта 2017 г. 18:46) |
Виктор Анатольевич, при развитии системы разработчики Компас ориентируются, прежде всего, на востребованность новых функций со стороны пользователей, большей частью которых являются инженеры-конструкторы. Поэтому, для обоснования необходимости внедрения кнопки “Построение КВП по любому набору точек и касательных” нужны примеры, демонстрирующие возможности ее практического применения. Такой пример у Вас тоже есть и приведен в статье "Кривые второго порядка в моделировании поверхностей". Соответсвенно это уже предложение по развитию функций моделирования поверхностей, но, как я понимаю, оно уже выходит за рамки "одной кнопки". Возможно есть и другие примеры, чем их больше тем лучше, тогда функцию "Построения КВП.." можно будет рассматривать в качестве базового алгоритма для множества функций. Вообще, я имею весьма косвенное отношение к разработке Компас. Компания АСКОН является разработчиком множества систем. Возможно, ваше предложение будет интересно разработчикам геометрического ядра C3D, лежащего в основе Компас. Постараюь донести его до них. Кроме того, уверен, что разработчкикам Аскон, будут интересны статьи, опубликованные на конференции. Буду всячески пропагандировать ее в компании. |

Короткий Виктор Анатольевич (12 марта 2017 г. 19:48) |
Петр Владимирович, спасибо за ответ и за совет. Вы правы. Нашими действиями управляет практическая потребность. Следующее мое "маркетинговое" действие будет таким. Для проверки точности и качества программы проверяющий вычерчивает у себя дома любое коническое сечение, тщательно фиксирует его метрику с максимально возможным числом знаков, выбирает на кривой любой (ЛЮБОЙ!) набор пяти точек и касательных (можно несобственные). Удаляет кривую. Присылает мне на почту уравнения касательных и координаты точек. Получает в ответ все метрические характеристики КВП с тем же числом знаков. То есть каноническое уравнение. Ну и проверяет - совпало или не совпало с его ответом. Единственное ограничение - не задавать точки в вершинах. Программа обижается и советует построить КВП известными из НГ методами. В качестве проверяющего может выступить любой участник конференции (проф. Хейфеца просим не беспокоиться). С уважением, Короткий В.А OSPOLINA@MAIL.RU |
|
Никифоров Петр Владимирович (12 марта 2017 г. 20:29) |
Уточняю название статьи: "Получение кривой теоретического профиля Жуковского для создания 3D-модели элемента аэродинамической компоновки крыла летательного аппарата".
|

Бойков Алексей Александрович (27 марта 2017 г. 22:15) |
Здравствуйте, уважаемый Петр Владимирович! Спасибо за этот и второй Ваш доклад. Было интересно как с точки зрения изучения возможностей "Компаса", так и с точки зрения применения системы "Симплекс" и конструктивной геометрии в целом. Считаю появление примеров совместного использования отечественных "Компаса" и "Симплекса" добрым знаком. С уважением, А.Бойков |
Назад Go Back