ПРОГРАММА 3D МОДЕЛИРОВАНИЯ ПРИ ПОСТРОЕНИИ РАЗВЕРТОК ПОВЕРХНОСТЕЙ

Конструирование разверток в инженерной практике встречается довольно часто, в то же время в программах дисциплин «Начертательная геометрия» и «Инженерная графика» теме «Развертки поверхностей» уделяется недостаточное внимание. Построение чертежей разверток вручную с помощью чертежных инструментов занимает большое количество времени, но не дает качественного результата, поскольку используется небольшое количество реперных точек. Компьютерное моделирование позволяет повысить точность и скорость создания разверток различных поверхностей.

Конструирование разверток в инженерной практике является необходимостью, особенно при работе с листовым материалом,  однако в программах  дисциплин «Начертательная геометрия» и «Инженерная графика» теме «Развертки поверхностей» уделяется недостаточное внимание.

В настоящее время в преподавании вышеуказанных дисциплин произошло разделение позиций, одни, высказываются за расширение применения компьютеров в черчении, другие, отдают предпочтение работе «вручную».

Особенно резко это происходит в прениях по поводу дисциплины «Начертательная геометрия».

Где же истина?  И что делать?

Авторами разработаны методики построения разверток с использованием графического пакета Inventor следующих поверхностей:

• усеченного конуса с недоступной вершиной, поверхности с ребром возврата,
• винтовой, кольцевой и ряда других поверхностей.

 Приведем алгоритм построения развертки винтовой поверхности.

В первом случае рассмотрим построение разверток традиционным способом [1].

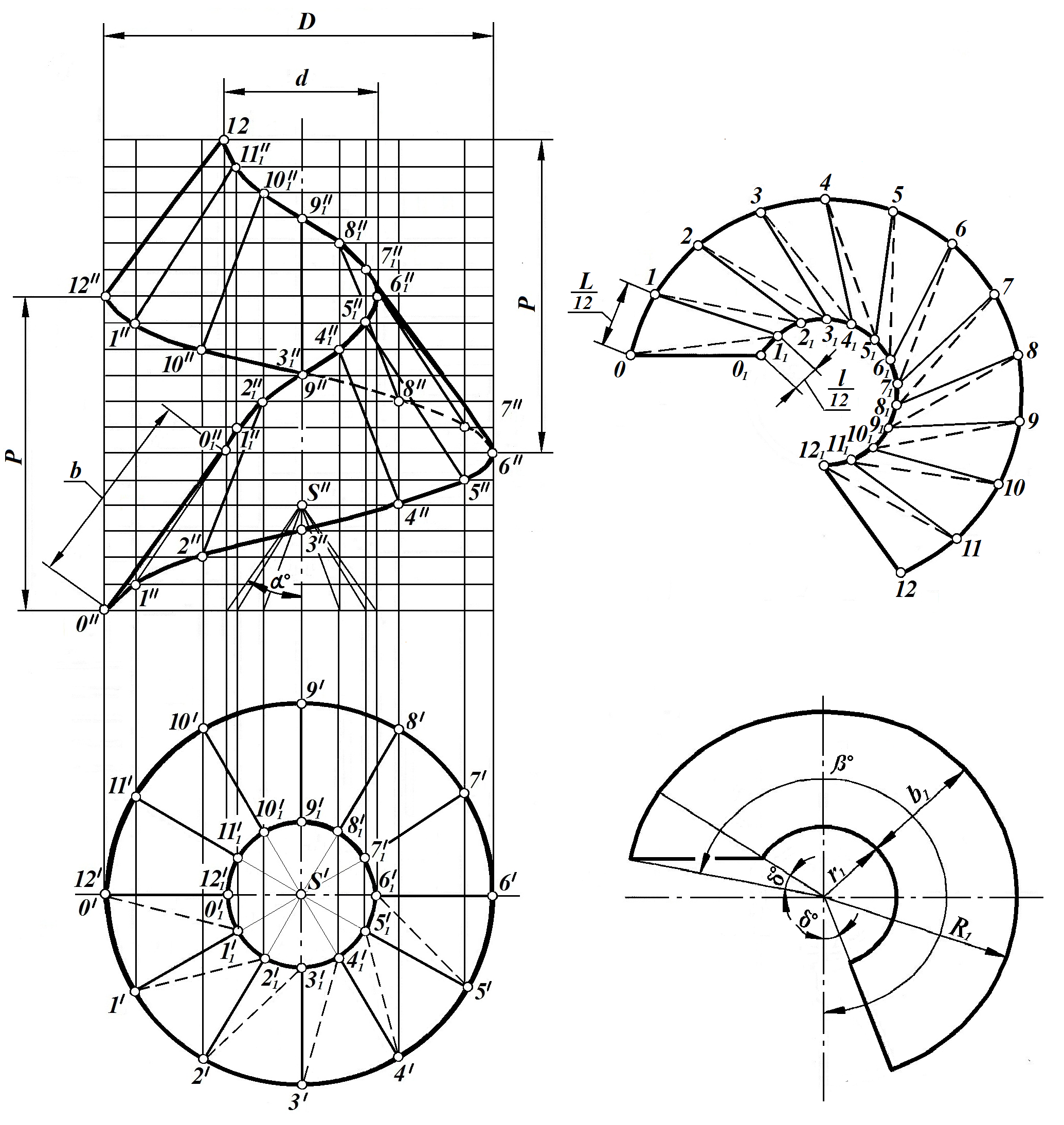
Для получения развертки винтовой поверхности используем ее ортогональные проекции.   Приведенная на рис. 1а винтовая поверхность представляет собой косой открытый геликоид. Поверхность  геликоида состоит из двенадцати частей, представляющих собой равные криволинейные четырехугольники 00₁11₁. Две противоположные стороны 00₁ и  11₁ – это отрезки равной длины, представляющие собой образующие линии поверхности геликоида.  Дуга винтовой линии  01  составляет одну двенадцатую часть дуги винтовой линии L.  Отрезок  0₁1₁ составляет одну двенадцатую часть дуги винтовой линии l.  L и l – длины винтовых линий в пределах шага  Р.  Величины сторон четырехугольника 00₁11₁  могут быть определены как графическим, так и аналитическим способами [ 2].

Развертка поверхности геликоида также может быть построена как графическим способом с помощью метода триангуляции (рис. 1б), так и аналитическим (рис. 1в).

Для построения развертки винтовой поверхности следует построить развертку одной двенадцатой части ее шага, то есть развертку криволинейного четырехугольника 00₁11₁. Затем для получения одного витка необходимо расположить двенадцать таких разверток рядом, учитывая, что  каждый отсек имеет с соседним отсеком общую образующую.

Необходимо отметить, что выполнение данного построения требует от студента аккуратности, внимательности, терпеливости и ряда других качеств, требующихся  будущему инженеру.

Во втором случае рассмотрим алгоритм построения развертки винтовой поверхности с помощью графического пакета Inventor.

Программа 3D моделирования Inventor компании Autodesk обеспечивают полный цикл проектирования разверток и создания конструкторской документации [3]. Приведем этапы построения.

Этап 1: В режиме «2D эскиза» командой  «отрезок», задаем ось винтовой поверхности.

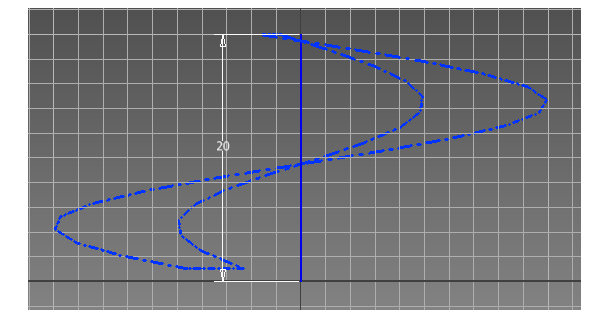
Этап 2: В режиме «3D эскиз» чертим  винтовую линию командой   «спираль» (рис.2). Выбираем тип винтовой линии: диаметр, шаг, высоту и направление. При этом высота должна быть равна шагу, а диаметр  соответствовать внутреннему диаметру винтовой части шнека.

Этап 3: В режиме «модель»   создаем  рабочую плоскость  по трем точкам: точки начала и конца оси и точку конца винтовой линии. В рабочей  плоскости создаем «2D эскиз»: строим из точки конца винтовой линии отрезок, который равен разности внутреннего и внешнего диаметров винтовой части шнека. Накладываем на этот отрезок «горизонтальную зависимость». Применяем команду «сдвиг». В качестве профиля выбираем отрезок, а траекторией  является винтовая линия. Создаем «3D эскиз», добавляя геометрию внешней и внутренней винтовых линий, которые задают поверхность. Убираем видимость у поверхности, полученной сдвигом (рис.3).

Этап 4: Вновь задаем винтовую поверхность с помощью команды «lофt»: отмечаем две винтовые линии и выбираем винтовую поверхность. Для винтовой поверхности  применяем команду  «толщина/подобие», указываем толщину, соответствующую толщине листового металла и выбираем в качестве результата  «тело».

Этап 5: Выбираем команды  «преобразовать в листовой металл»  и «параметры листового металла». Снимаем выделение в пункте  «использовать толщину» и указываем толщину. Создаем развертку соответствующей командой (рис.4).

Выводы:

1. Построение развертки винтовой поверхности (как и других поверхностей) можно производить как графическим «ручным», так и  компьютерным способом;
2. Компьютерный способ отличается более высокой точностью построения;
3. Графический способ позволяет лучше проводить анализ, синтез и преобразования геометрических фигур, составленных из различных элементов;
4. Компьютерный способ отличается более высокой скоростью построения;
5. Необходимо не противопоставлять компьютерную графику начертательной геометрии, а постараться найти элементы их соприкосновения и дополнения, учитывая, что термин «винтовая поверхность» возник задолго до появления компьютеров.

Список литературы

1. Бубенников А.В.  Начертательная геометрия. Учебник  для  втузов. М.: Высшая школа, 1985. -288 с.
2. Высоцкая Н.Н., Иерусалимский А.М., Невельсон Р.А., Федоренко В.А. Технические развертки изделий из листового материала. М.: Машиностроение, 1968. – 272 с.
3. Гузненков В.Н., Журбенко П. А. Autodesk Inventor 2012. Трехмерное моделирование    деталей и создание чертежей. Изд. ДМК-Пресс. 2012. 120 с.

Рисунки к докладу

Хейфец Александр Львович (13 марта 2017 г. 0:32)	Владимир Игоревич (как первый автор). Так каую поверхность Вы развернули: наклонный геликоид или эволвентный геликоид?.Если эвольвентный (торс) то все ОК. Если геликоид наклонный (а по рисункам, вроде, он), то он, насколько помню, неразвертываемая поверхность. По моему из линейчатых - только торс (эвольвентный геликоид), конус и цилиндр.  Если ошибаюсь - поправьте. Иначе - развертка получается приближенная и необходима оценка ее  точности (погрешности). С уважением. А.Л. Хейфец
Сальков Николай Андреевич (13 марта 2017 г. 3:45)	Александр Львович, судя по рис. 1, это - косой закрытый геликоид. У открытого образующая должнв касаться некоторого цилиндра вращения, а здесь образующая пересекает ось. Судя по рис. 2, это - прямой закрытый (образующая явно должна пересекать ось, при этом оставаясь параллельной плоскости параллельности) геликоид. По аксонометрии (рис. 3) сказать трудно, видно только, что это, по-видимому, прямой геликоид.
Федоренко Владимир Игоревич (14 марта 2017 г. 1:48)	Уважаемый Александр Львович! Во-первых, приношу извинения за достаточно глупые ошибки в работе. На рис.1 косой закрытый геликоид, а не открытый. Торопливость подготовки не оправдание. Во-вторых, Вы не ошиблись, только эвольвентный геликоид называют  развертывающимся. (Эвольвентный геликоид образуется движением прямолинейной образующей, остающейся во всех своих положениях касательной к цилиндрической винтовой линии, являющейся ребром возврата. Если проанализировать рис.4, то видно, что прямолинейные участки развертки пересекаются в центре. Следовательно, геликоид точно не эвольвентный. Иначе они были построены по касательной к некоторой внутренней окружности. Остается - прямой закрытый геликоид. Это я позволил себе продолжить анализ Николая Андреевича Салькова. Замечание об оценке точности (погрешности) - это продолжение нашей дальнейшей работы. Спасибо Вам  за него.
Рукавишников Виктор Алексеевич (24 марта 2017 г. 21:03)	Добрый день, Владимр Игоревич! Мне понравилось ваше предложение приехать к Вам в университет и выступить. В спокойной обстановке обсудить наши общие проблемы. И действовать сообща на благо нашего общего дела. Спасибо! В рамках этого форума сложно  найти верное решение.  Мне кажется, мы пересекались с Вами  2-3 года назад в Autodeske. Я был вместе Энвером Фазлулиным у Постельника. Вы работали в МАМИ? Я лично знаком и с Владимиром Николаевичем Гузненковым. Думаю, что он тоже будет не против. Давайте подумаем как это сделать. Может будут какие-то конференции у Вас или в др. университете. Можно просто прислать приглашение. Чем быстрее это произойдет, тем лучше для нашего образования в целом. Мой электронный адрес есть у В.Н. Гузенкова. Можете зайти информацию и на сайт Казанского гос. энергетического университета.  С уважением, В.А. Рукавишников.