В статье рассматривается задача анализа гладкости кривых методом эпюр. Показан конструктивно-геометрический подход к разработке функций САПР.
Ключевые слова: Геометрическое моделирование, анализ гладкости, САПР
В вопросах конструирования сложных технических объектов важное место занимают исследования свойств поверхностей, например: выявление зон с отрицательной, положительной и нулевой кривизной, определение особых точек, линий и т.п., в т.ч. визуально, по изображению сконструированной поверхности или ее каркаса на экране дисплея, с целью оценки ее функциональных, эстетических, геометрических качеств.
Так, например, гладкость является наиболее общим требованием, предъявляемым к геометрической модели аэродинамической поверхности. Для обеспечения гладкости важна не только непрерывность производных, но и ограниченность их изменения на малом отрезке, т.е. плавность изменения графика кривизны [1].
Для обеспечения возможности проведения анализа гладкости кривых и поверхностей, разработчики САПР внедряют в свои системы соответствующие функции (например, построение эпюр кривизны). В отсутствии готового решения, задача может быть выполнена посредством прикладного интерфейса программирования САПР, что требует от пользователя не только знаний предметной области, но и опыта разработки программного обеспечения. Поэтому, если исходная задача (проектирование формы) является чисто геометрической (конструктивной), выбор конструктивно-геометрической модели предпочтителен при условии достаточно развитой для ее создания и функционирования теоретической базы. Аналитическое представление может играть здесь вспомогательную роль [2].
В аналитической геометрии кривизна плоской линии определяется через понятие предела [3] следующим образом: пусть при переходе от точки M линии L к точке M' (рис. 1) касательная, направленная в сторону движения, переходя из положения MT в положение M'T' поворачивается на угол ɷ. Отношение угла ɷ к длине дуги MM' характеризует искривленность линии L на участке MM' и называется средней кривизной дуги MM'.
Кривизной линии L в точке M называется предел, к которому стремится средняя кривизна дуги MM' когда точка M' стремится к M. Кривизна обозначается буквой К.
Выясним геометрический смысл радиуса кривизны плоской линии (см. рис. 2а). Пусть точка M1, двигаясь по плоской линии L стремится к неподвижной точке M2, где кривизна К не равна нулю. Тогда точка С1, где неподвижная нормаль о12 пересекается с нормалью о12 стремится к точке С2, отстоящей от M2 на расстояние M2С2 = 1/К *). При этом луч M2С2 направлен в сторону вогнутости линии L.
Отрезок M2С2 называется радиусом кривизны, точка С2 — центром кривизны линии (для точки M2). Аналогичные построения еще для дополнительных точек M4 и M5 дадут отрезки M3С3, M4С4 (радиусы кривизны) и точки С3 и С4 (центры кривизны) линии L в точках M3 и M4 соответственно (см. рис. 2б). Радиус кривизны изменяется от точки к точке. Таким образом, попарное пересечение нормалей, проведенных через ближайшие точки плоской кривой, позволяет найти радиус ее кривизны в каждой из этих точек.
Выполнение построений, приведенных на рис. 2, в системе геометрического моделирования Симплекс, позволило задать множество точек Mn посредством интервального ряда, содержащего n значений в диапазоне, определенном длиной сплайна произвольной формы (либо его участка). Используем эту модель в качестве основы геометрического алгоритма анализа гладкости кривых методом эпюр.
Вычислим величину радиуса кривизны Rn – расстояния между каждым экземпляром множества точек Mn и соответствующими экземплярами множества центров кривизны Сn. Для управления размером эпюр введем величину rn, как отношение масштабного коэффициента km к радиусу кривизны Rn. На расстоянии rn от точек Mn, в направлении, обратном направлению нормалей о1n, построим точки Bn. Проведя множество отрезков между точками Mn и Bn, получим эпюры, визуализирующие относительную кривизну линии. Проведем через множество точек Bn сплайн, огибающий эпюры.
В заключении определим входные и выходные параметры алгоритма для применения его в виде новой функции системы (см. рис. 3). Теперь для построения эпюр кривизны достаточно вызвать созданную функцию, указать кривую (сплайн) и дополнительные параметры отображения: коэффициент масштабирования и количество эпюр.
Результат работы алгоритма, созданного в системе Симлекс, рассмотрим в сравнении с аналогичной функцией САПР NX фирмы «Siemens PLM Software». В качестве исходных данных использованы дискретные точечные базисы аэродинамических профилей, полученные: напрямую из математической модели (рис. 4а), рассмотренной в статье [4]; путем замера экспериментальной модели (рис. 4б), исследование которой проводилось в ФГУП «СибНИА им. С.А. Чаплыгина».
*) Доказательство приведено в книге [3], с которым можно ознакомитсяа по прямой ссылке
Список литературы
- Ерохин Александр Павлович Применение методов условной оптимизации при сглаживании точечно заданных аэродинамических обводов, МАИ, — 4 с.
- Волошинов Д.В. Теория автоматизации проектирования объектов и процессов на основе методов конструктивного геометрического моделирования, Диссертация на соискание ученой степени доктора технических наук. — СПб., 2010, —363 с.
- Выгодский М.Я. Справочник по высшей математике, М., "Наука", 1977 г. —872 с.
- Никифоров П.В. Получение кривой теоретического профиля Жуковского для создания 3D-модели поверхности крыла. [Электронный ресурс] VII международная интернет-конференция «Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации» КГП-2017. URL: http://dgng.pstu.ru/conf2017/papers/62/ (дата обращения: 03.11.2017).
Рисунки к докладу
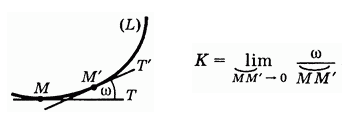
Рис. 1
Определение кривизны через понятие предела
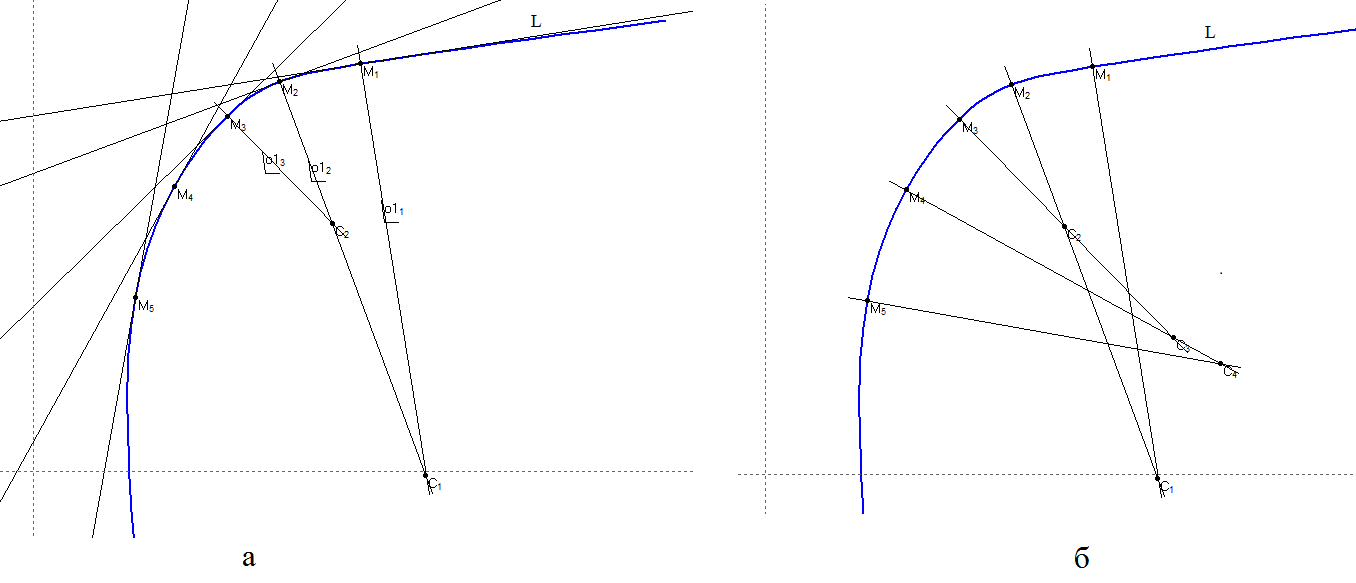
Рис. 2
Геометрический смысл радиуса кривизны
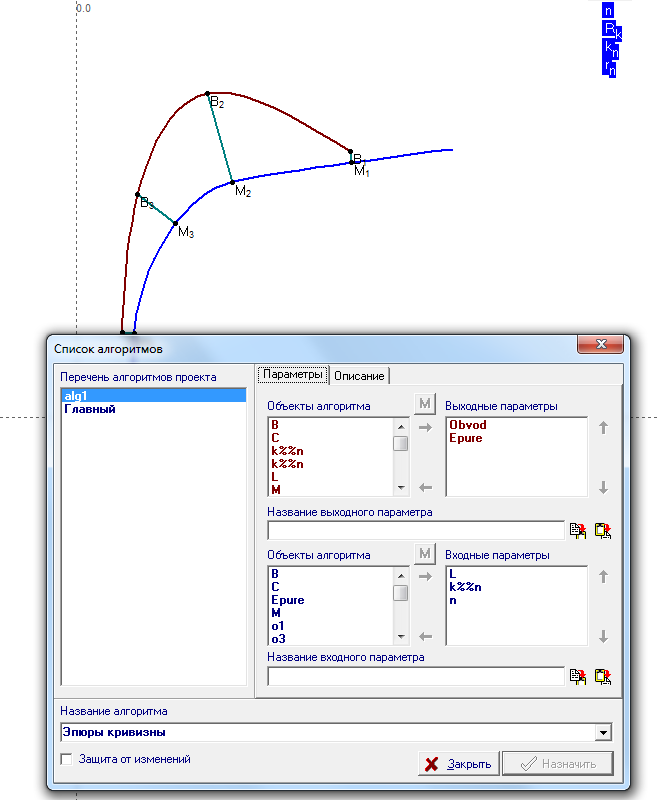
Рис. 3
Задание параметров геометрического алгоритма в Симплекс
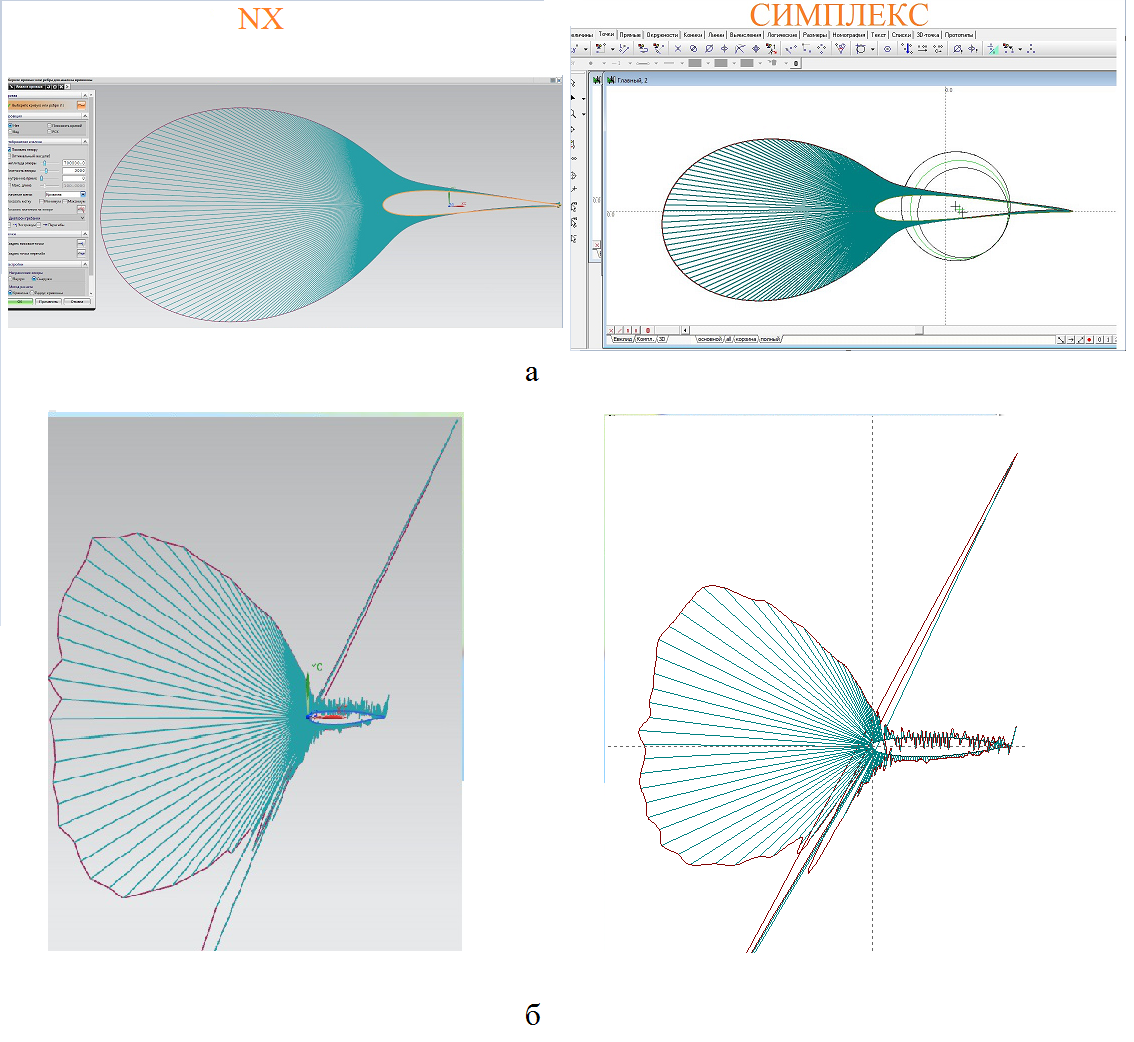
Рис. 4
Вопросы и комментарии к выступлению:

Селиверстов Александр Владиславович (12 марта 2017 г. 12:55) |
Здравствуйте, Петр Владимирович! |
|
Никифоров Петр Владимирович (12 марта 2017 г. 19:00) |
Здравствуйте, Александр Владиславович! Опыта преподавания геометрии у меня нет ни в каком виде :). По роду деятельности я постоянно изучаю различные научные работы. В своих докладах я просто постарался "придерживаться стиля" так сказать, но не углубляясь в подробное обоснование решений. |
Назад Go Back