УЧЕБНОЕ ЗАДАНИЕ "ПЛОСКИЕ ОБВОДЫ"

Рассмотрены варианты построения гладких составных кривых (обводов), проходящих через заданные точки и удовлетворяющие дополнительным граничным условиям. Использованы кубические параметризованные параболы в векторной форме. Даны примеры выполнения заданий.

Введение

Обводом называется линия, составленная из дуг кривых выбранного вида, которые в стыковых точках имеют определенный порядок соприкосновения [1, 2]. Учебное задание по построению обводов предназначено для студентов технических специальностей, изучающих инженерную компьютерную графику. Компьютерная графика – это не только 3D-моделирование. Это деятельность человека, в которой компьютер используется для создания изображений и работы с ними. Теоретической основой компьютерной графики является вычислительная геометрия, сформировавшаяся в самостоятельную научную и учебную дисциплину во второй половине 20 века.

Учебники или монографии по вычислительной геометрии трудно читать. Совсем не просто использовать их в конструкторской работе. Вычислительная геометрия – своеобразный синтез начертательной геометрии, информатики, векторной алгебры, дифференциальной геометрии, анализа.

Значит, достаточно разобраться с этими учебными предметами? Нет, недостаточно. Учащийся встречается с большим количеством совершенно новых для него геометрических форм и алгебраических многообразий, которые не рассматриваются в смежных учебных дисциплинах. В результате у студента возникает множество вопросов. Что такое сплайн? Чем алгебраический сплайн отличается от геометрического? Что такое полином Эрмита? Параметрическая кривая в форме Фергюсона? В форме Безье? NURBS-кривые? Чем они отличаются? Как практически построить на компьютере кривую гладкостью второго порядка, имеющую в заданных точках заданные касательные и радиусы кривизны?

И вообще, что такое радиус кривизны? Кажется, мы это где-то проходили. Или что такое векторная функция скалярного аргумента, которую в учебнике называют страшным словом “годограф”? Да как вообще такое возможно – аргумент скалярный, а функция векторная? А ведь еще есть поверхность Кунса и другие составные поверхности. Как спроектировать отсек поверхности, чтобы он гладко сопрягался с соседними поверхностями? Какие есть способы формирования поверхностей, кроме кнопки loft, предназначенной вовсе не для конструктора-проектировщика?

Список вопросов очень велик. На них надо не просто отвечать определениями из Википедии, а давать студенту живые геометрические примеры и решать конкретные конструкторские задачи по проектированию линий и поверхностей с использованием графоаналитических инструментов, разработанных в компьютерной графике за очень небольшое время ее существования.

Конечно, если мы готовим юзеров, то вполне достаточно показать кнопку, где написано “сплайн” или “кривая Безье”. Учащийся это четко поймет, и на вопрос, что такое сплайн, немедленно ответит, что это кнопка, которая чертит красивую кривую через указанные им, студентом, точки.  Разве это плохой результат обучения? Это очень хороший результат учебного процесса. Это компетенция, востребованная в его будущей профессиональной деятельности.

Но чтобы не просто пользоваться, а еще и немного понимать, чем мы пользуемся, надо заглянуть под кнопку. Разумеется, если мы используем ПК для моделирования болтов с ювелирно выполненной в 3D строго по стандарту метрической резьбой вместе со сбегом, недорезом, фасками, галтелями и прочими аксессуарами, то под кнопки заглядывать не надо. Если же мы намерены предложить студенту базовые, фундаментальные геометрические знания, а не только специальные приемы 3D-моделирования в версии Solid-2013 или Компас-16, то должны объяснить, что сплайн – это не просто значок на панели инструментов.

Да, студенты изучают и аналитическую геометрию, и векторную алгебру, и анализ, и информатику, и основы программирования. Но все это происходит в совершеннейшем отрыве одно от другого и вообще от всего. И в первую очередь – в отрыве от геометрии. Кажется, назрела потребность в полноценном учебнике компьютерной графики, в котором будут не только ответы на поставленные выше вопросы, но и примеры реального моделирования кусочно-гладких двухмерных и трехмерных обводов, и самые разные конструкторские задачи, и задания для самостоятельной работы.

Задание 1. Векторная параметризация кубической параболы

Требуется провести алгебраическую кривую y=f(x), касающуюся единичных векторов T₀, T₁ в указанных точках P₀, P₁ (рис. 1). Найти ее уравнение (здесь и далее жирным шрифтом выделены векторы).

С помощью кнопки “сплайн с защемленными концами” мы немедленно начертим искомую кривую. Но кнопка не дает уравнение кривой. К тому же задача так проста, что для ее решения не нужна составная кривая. Мы сумеем найти кривую, описываемую одним алгебраическим уравнением.

Прямая, соединяющая данные точки, не годится. Значит, надо повышать порядок искомой кривой. Будем ее искать среди кривых второго порядка (КВП). Множество КВП на плоскости пятипараметрично. Четыре геометрических условия выделяют из множества КВП однопараметрическое семейство кривых. Следовательно, задача не только вполне разрешима среди множества КВП, но даже допускает указание еще одного условия. Например, можно указать промежуточную точку конструируемой кривой, после чего построить кривую методом инженерного дискриминанта.

Задача решена, но при этом возникли две проблемы. Во-первых, найти уравнение КВП в заданной системе декартовых координат довольно хлопотно. Впрочем, можно применить программу “Компьютерный коникограф”, которая немедленно укажет численные значения коэффициентов канонического уравнения начерченной КВП и ее положение в заданной системе координат. Другая проблема связана с геометрией искомой кривой. Дело в том, что нам назначили направление движения от P₀ к P₁, указав касательные векторы T₀, T₁. С помощью КВП это требование невыполнимо: выходя из P₀ в направлении T₀, мы придем в точку P₁ против направления T₁. Значит,  от КВП, как и от кнопочного сплайна, также придется отказаться. Приходится искать ответ среди кривых третьего порядка.

Общее уравнение кубической кривой приводится к одной из четырех канонических форм, среди которых наиболее привлекательно выглядит кубическая парабола

y=a₀+a₁x+a₂x²+a₃x³.                                    (1)

В чем ее преимущество? Во-первых, простота. Среди алгебраических кривых самой простой является, конечно, прямая линия, затем КВП, затем кубическая парабола. Кривая (1) замыкает тройку самых простых алгебраических кривых. Другое, гораздо более важное преимущество кубической параболы перед КВП, состоит в наличии у нее точки перегиба, то есть точки с нулевой кривизной, что, собственно, и привело к широким приложениям этой замечательной кривой в проектировании.

Кубическая парабола настолько важна в вычислительной геометрии и компьютерной графике, что следует подробнее рассмотреть ее строение. Уравнение (1) преобразуется к виду

y=a(x³–px)                                    (2)

параллельным переносом системы координат xy. На этом свойстве основано вычисление корней кубического уравнения по формуле Кардано. Уравнение (2) описывает двупараметрическое семейство кривых. Изменение параметра a эквивалентно аффинному растяжению вдоль оси y с неподвижной прямой x (масштабирование по y). Параметр p определяет форму кривой. При отрицательном значении p получаем кривую без экстремумов с ненулевой первой производной в точке перегиба. При p=0 кривая (2) имеет в точке перегиба горизонтальную касательную (производная равна нулю). При положительных значениях p получаем кривую с двумя экстремумами (рис. 2).

Подсчитаем число степеней свободы кубической параболы. Поворачивая двухпараметрическое множество кривых (2) около начала координат, получаем трехпараметрическое семейство парабол с общей точкой перегиба. Произвольно перемещая это семейство по плоскости, получаем ∞² трехпараметрических множеств. Следовательно, множество кубических парабол пятипараметрично. Иначе говоря, кубическая парабола на плоскости имеет пять степеней свободы.

Здесь надо особо отметить, что уравнение (1), записанное в фиксированных декартовых координатах xy, не разрешает поворот. Все параболы вида (1) имеют оси, параллельные осям координат x, y. Поэтому уравнение (1) описывает ∞⁴ парабол. Парабола вида (1) имеет не пять, а всего четыре степени свободы.

Это ограничение свободы не затрудняет выполнение задания, поскольку в нем на искомую кривую наложено именно 4 условия. Поэтому будем искать решение в форме (1). Подставляя в (1) координаты концевых точек P₀, P₁, получаем два линейных уравнения относительно неизвестных коэффициентов. Дифференцируя и подставляя известные значения производных на концах участка, получаем еще два уравнения. Все в порядке. Четыре линейных уравнения связывают четыре неизвестных коэффициента. После вычисления коэффициентов уравнения (1) студент вычерчивает на компьютере кривую. Задание выполнено. Решение единственное.

Но именно это обстоятельство (единственность решения) настораживает. Конструктору, как правило, нужен выбор, вариативность решения. К тому же множество кубических парабол на плоскости, как мы показали, пятипараметрично. Значит, указание четырех условий должно оставлять нам богатый выбор кубических парабол, а мы нашли только одну. Где остальные?

На этот вопрос нетрудно ответить. Представив уравнение параболы в канонической форме (1), мы фактически запретили поворот осей, то есть забрали у искомой кривой одну степень свободы. Вернем ее, записав уравнение (1) не в бетонных декартовых координатах, а в “подвижной” векторной параметризованной форме:    

r(t)=a₀+a₁t+a₂t²+a₃t³.                                    (3)

Уравнение (3) задает векторную функцию r скалярного параметра t. Преподавателю придется потрудиться, объясняя геометрический смысл этого уравнения. Придется объяснить, почему парабола (3) обладает пятью степенями свободы, хотя независимых векторных коэффициентов a_i при скалярной переменной t всего лишь четыре. Причина в том, что в результате учета граничных условий появляются так называемые “весовые коэффициенты”. Их не видно в уравнении (3), они пока “спрятаны” в векторах a_i. Конечно, если мы наложим на кривую пять условий, то никаких степеней свободы у параболы не останется. Весовых коэффициентов не будет. Но в рассматриваемом задании дано 4 граничных условия – концевые точки P₀, P₁ и касательные векторы в этих точках, поэтому в процессе решения обязательно появится пара весовых коэффициентов, вариативность которых доставляет пятую степень свободы. Это означает, что имеется ∞¹ кубических парабол с защемленными концами, удовлетворяющих условиям задания.

Вернемся к заданию. Введем в рассмотрение единичные орты i, j, совместив их с осями координатной системы x, y, в которой были даны граничные условия. Будем считать, что параметр t меняется от 0 в точке P₀(x₀, y₀) до единицы в точке P₁(x₁, y₁). Тогда при t=0 (в точке P₀) имеем

r(0)=a₀=x₀i+y₀j.                                           (4)

При t=1 (в точке P₁) получаем:

r(1)=a₀+a₁+a₂+a₃= x₁i+y₁j.                            (5)

Дифференцируя (3), находим производную векторной функции r по скалярному аргументу t:

r′(t)=a₁+2a₂t+3a₃t².                                            (3′)

Здесь следует остановиться и сделать пояснения. В (3′) нам придется подставлять граничные условия. Они заданы. Но производная векторной функции – вектор! Вектор имеет направление и модуль. Направление этого вектора мы знаем: оно задано на концах искомой кривой единичными касательными векторами T₀, T₁. Но чему равны модули этих векторов?

Мы не будем здесь рассматривать отличие производных скалярной и векторной функций. Это отличие обязательно надо объяснить студентам, хотя, разумеется, они это “проходили” на уроках математики, но либо прошли мимо, либо забыли. Это материал первого семестра. Просто согласимся с тем, что поскольку мы пока еще не нашли искомую кривую, то и ее производные в граничных точках пока не вполне известны. Направления T₀, T₁ этих производных знаем, а модули нет. Ограничимся тем, что обозначим неизвестные модули |r′(0)|=α₀ и |r′(1)|=α₁ и временно причислим их к неизвестным.

С учетом принятых обозначений можно записать еще два условия, налагаемые на коэффициенты кривой (3):

r′(0)=a₁=α₀T₀,                                               (6)

r′(1)=a₁+2a₂+3a₃=α₁T₁.                                  (7)

Таким образом, получены четыре уравнения (4…7), в которые входят четыре неизвестных векторных коэффициента a₀… a₃ и две скалярные величины α₀, α₁, которые называют “весовыми коэффициентами”. Собственно, геометрический смысл весовых коэффициентов вполне понятен: с увеличением веса α₀ конструируемая парабола “теснее” прилегает к направлению касательного вектора T₀ в начальной точке P₀, а при увеличении α₁ – к вектору T₁ в точке P₁. То есть изменение α₀, α₁ изменяет кривизну конструируемого обвода в точках P₀, P₁. Поэтому весовые коэффициенты α₀, α₁ не надо определять из системы уравнений (4…7). Да это и невозможно, потому что уравнений четыре, а неизвестных шесть. Коэффициенты α₀, α₁ – это параметры, управляющие формой (“полнотой”) конструируемой линии.

Далее студенту предстоит выполнить рутинные, но требующие внимания алгебраические преобразования, чтобы извлечь из (4…7) коэффициенты a₀… a₃. Он получит следующий результат:  

a₀=x₀i+y₀j,

a₁= iα₀cosδ₀+jα₀sinδ₀,

a₂=(3Δx-2α₀cosδ₀-α₁cosδ₁)i+(3Δy-2α₀sinδ₀-α₁sinδ₁)j,

a₃=(α₀cosδ₀+α₁cosδ₁-2Δx)i+(α₀sinδ₀+α₁sinδ₁-2Δy)j.

Здесь использованы обозначения Δx=x₁-x₀, Δy=y₁-y₀, δ₀ и δ₁ – углы наклона касательных векторов T₀, T₁ к оси x. Подставляя сюда конкретные числовые значения величин x₀, y₀, Δx, Δy, δ₀, δ₁, получаем зависимость векторов a₀… a₃ от весовых коэффициентов α₀, α₁. Любое сочетание весовых коэффициентов α₀, α₁ индуцирует уравнение кубической параболы в форме (3), удовлетворяющей заданным граничным условиям. Параметр t изменяется в диапазоне от 0 (точка P₀) до единицы (точка P₁).

Теперь перед преподавателем встает очередная задача – надо объяснить, что два варьируемых весовых коэффициента дают не двухпараметрическое, а всего лишь однопараметрическое множество парабол. Возьмем произвольное значение α₀, например, α₀=3. Меняя α₁, получаем однопараметрическое семейство g₁ парабол (3), примерно одинаково прилегающих к T₀ в точке P₀, но с различным усердием прилегающих к вектору T₁ в точке P₁. Теперь фиксируем произвольное значение α₁, например, α₁=5, и меняем α₀. Получаем другое однопараметрическое семейство парабол g₀. Очевидно, парабола с весовыми коэффициентами α₀=3, α₁=5 – общая для семейств g₁ и g₀. И вообще, любой паре весовых коэффициентов α₀, α₁ в семействах g₁ и g₀ отвечает общая парабола. Следовательно, g₁ и g₀ – одно и то же множество. Тождественное совпадение двух однопараметрических множеств дает однопараметрическое множество. Варианты обвода для трех сочетаний весовых коэффициентов представлены на рис. 3.

Конечно, мало найдется таких студентов-ботаников, которые осилят все эти “если – следовательно”. Но, выполняя задание 1, кое-чему научится самый средний студент, а может быть, даже и преподаватель, так далеко ушедший в инновационных методиках преподавания на принципиально новый уровень, что слегка подзабыл алгебру, а заодно и геометрию.

Осталось отметить, что (3) – это кубическая параметрическая кривая в форме Фергюсона (1963 г.). С нее началось эффективное развитие компьютерных методов проектирования [3]. Кубическую параболу, построенную в первом задании  по двум точкам и векторным производным в этих точках, называют кубической кривой Эрмита, по аналогии с интерполяционным полиномом Эрмита, для расчета коэффициентов которого используются значения функции и ее производных в заданных точках [4].

   Задание 2. Алгебраический сплайн второго порядка гладкости

Задание 2 почти полностью совпадает с заданием 1, но с небольшим отличием. Требуется не просто провести гладкую кривую, касающуюся единичных векторов T₀, T₁ в указанных точках P₀, P₁, но эта кривая должна пройти через некоторую промежуточную управляющую точку R. Иначе говоря, на искомую кривую наложено не четыре, как в первом задании, а пять условий.

На помощь сразу приходит способ инженерного дискриминанта. Через три точки P_0, P₁, R с указанными в двух точках касательными проходит единственная КВП. Ее недостаток тот же, что в задании 1 – не обеспечивается заданное направление касательных векторов. Отказываемся.

Возвращаемся к кубической параболе в форме (3). Однопараметрическое множество парабол (3) с заделкой концов покрывает всю плоскость. Но выделить искомую кривую, найти весовые коэффициенты α₀, α₁ параболы, проходящей через конкретную точку R, будет непросто. Эта нетривиальная задача приведет нас к громоздким алгебраическим манипуляциям.

Вернемся к кубической параболе

y=a₀+a₁x+a₂x²+a₃x³                               (1′)

в привычных декартовых координатах. Конечно, она не слишком подвижна, у нее фиксированное направление осей, вследствие чего она имеет лишь четыре степени свободы. Для решения нашей задачи этого явно недостаточно, поскольку мы требуем выполнения пяти условий. Попробуем составить искомую кривую из двух кубических парабол.

Запишем уравнения участков y=P₀R и y=RP₁ в виде

y=a₁x³+b₁x²+c₁x+d₁,                    (8)

y=a₂x³+b₂x²+c₂x+d₂.                    (9)

Для определения неизвестных коэффициентов a_i, b_i используем граничные условия на концах P₀ (x₀,y₀), P₁(х₁,y₁) конструируемой кривой, а также условия равенства координат и производных в стыковой точке R(x_R,y_R).

В точке P₀ имеем

y₀=a₁x₀³+b₁x₀²+c₁x₀+d₁,                                           (10)

y′(x₀)=tgδ₀=3a₁x₀²+2b₁x₀+c₁,                                   (11)

где δ₀ – угол наклона касательной в точке P₀. В точке P₁ имеем условия:

y₁=a₂x₁³+b₂x₁²+c₂x₁+d₂,                                            (12)

y′(x₁)=tgδ₁=3a₂x₁²+2b₂x₁+c₂,                                    (13)

где δ₁ – угол наклона касательной в точке P₁.

В стыковой точке R(x_R,y_R) должны быть равны “левые” и “правые” первые и вторые производные

6a₁x_R+2b₁=6a₂x_R+2b₂,                                   (14)

3a₁x_R²+2b₁x_R+c₁=3a₂x_R²+2b₂x_R+c₂.               (15)

Значения самих функций в точке R должны быть равны заданным:

a₁x_R³+b₁x_R²+c₁x_R+d₁=y_R,                                 (16)

a₂x_R³+b₂x_R²+c₂x_R+d₂=y_R.                                 (17)

Таким образом, для определения восьми неизвестных коэффициентов в уравнениях (8, 9), описывающих составную кривую второго порядка гладкости, получаем восемь линейных уравнений (10…17). Подставляя в эти уравнения заданные численные значения граничных условий x₀, y₀, x₁, y₁, tgδ₀, tgδ₁ и координаты промежуточной точки x_R, y_R, получаем систему восьми линейных алгебраических уравнений (СЛАУ) относительно неизвестных коэффициентов a_i, b_i. Очевидно, ее решение “вручную” на калькуляторе нецелесообразно, да практически и невозможно. Обращаемся в программу Mathcad, где для решения СЛАУ используется команда lsolve. Например, при граничных условиях x₀=0, y₀=0, x₁=2, y₁=1, tgδ₀=1, tgδ₁=2 и координатах управляющей точки  x_R=1, y_R=0.5 получается обвод, состоящий из двух парабол y=-0.5x²+x (при изменении x от 0 до 1) и y=x³-3.5x²+4x-1 (при изменении x от 1 до 2). Первый участок при рассматриваемом частном сочетании граничных условий выродился в квадратичную параболу. В узловой точке R обеспечено соприкосновение второго порядка гладкости (рис. 4, а).

Очень важно, чтобы студент не просто теоретически решил задачу построения обвода, но довел решение до числа, до уравнения, до графика. Только тогда это будет инженерное, конструкторское решение. Только тогда у него возникнет естественный вопрос: а если управляющих точек будет не две, а три? Ведь это приводит к определителям с размером не 8, а уже 12. Это еще терпимо. А если 10 или 20 точек? Какие же будут определители? И какова будет точность их вычисления? Только с этого момента, с момента появления вопросов, с момента большого непонимания начинается процесс обучения.

Только после самостоятельного выполнения какого-нибудь простенького задания по моделированию обводов можно будет рассказать о сплайнах, о трехдиагональных матрицах и методе прогонки, о программных средствах для их реализации. А заранее отвечать на незаданные вопросы бесполезно.

Это сложно? Да, сложно. Сложно и для студентов, и для преподавателей, которые немедленно укажут, что эти компетенции (например, знание анатомии сплайна) не востребованы в будущей профессиональной деятельности инженера-конструктора. А поскольку не востребованы, то и учить не надо. Спокойнее и проще заниматься востребованным трехмерным моделированием.

А как хороша начерталка в 3D! Ведь это чудо. Мечта Гаспара Монжа осуществилась. Все так наглядно. На Западе давно не чертят. Возьмите, например, новейший западный учебник геометрии [5]. Это третье издание, то есть он востребован. И очень толст. Ни единого чертежа! Ни одного! Цветные картинки и фотографии. Нет там проекционных чертежей. Вдруг студент не поймет? Например, у него плоховато с объемным восприятием. А мы его обидим чертежами. Надо терпимее, толерантнее. Показал студенту геликоид в 3D. Понял, что такое геликоид? Молодец. Теперь сделай сам. Видишь вот эту кнопку? Нажми, не бойся. Появится спираль. И так далее. К концу урока получится геликоид.

А инженерная графика! Какие чертежи, какие проекции? Забудьте. Не востребованы. Теперь все в 3D. Безбумажная и безчертежная технология. Вращать, выдавить, обрезать, лофтировать, отрендерить. Красота! Руководство одобряет 3D, ректор технического ВУЗа запрещает ручное черчение! Ну и хорошо, начальство лучше знает. Электронная модель изделия! Ярко, современно, инновационно!

Эти “инновации”, сводящиеся по сути своей к замене всей ГГП трехмерным моделированием, безнадежно устарели и стали серьезным препятствием на пути образовательного процесса. Ну когда, наконец, мы поймем, что нельзя сводить ГГП к бесконечному 3D-моделированию фитингов?

   Задание 3. Обвод с заданной кривизной в конечных точках

Снова вернемся к заданию 1, но усилим граничные условия. Пусть требуется   провести обвод с заданными касательными в точках A(x_A,y_A), D(x_D,y_D), имеющий в этих точках заданную кривизну. Найти уравнения участков обвода.

Будем искать решение среди кубических парабол. Очевидно, не существует кубической параболы, удовлетворяющей заданным условиям. Действительно, на искомую кривую наложено шесть условий (две точки, две касательные, две окружности кривизны), а у кубической параболы всего 5 степеней свободы. Как быть?

Попробуем составить обвод из двух дуг кубических парабол вида (1). При этом следует учесть, что парабола (1) жестко привязана к декартовой системе координат, поэтому у нее всего 4 степени свободы. Нетрудно видеть, что задача не решается двумя параболами. Действительно, на первый участок наложены условия прохождения через P₀ (минус одна степень свободы), задано направление касательной в точке P₀ (минус еще одна степень свободы), задана кривизна (отнимаем еще одну степень свободы). То есть простое выполнение граничных условий в начальной точке обвода оставляет первому участку всего одну степень свободы. То же самое относится ко второму участку. В результате остается всего две степени свободы, с помощью которых невозможно гладко состыковать участки обвода с общим кругом кривизны в точке стыка.

Для решения задачи есть несколько вариантов. Можно, например, продолжать поиск среди кубических кривых, но перейти к кубическим кривым общего вида, обладающим девятью степенями свободы. Этого нам точно хватит.

Можно остаться в “классе” парабол, но повысить размерность и искать ответ в виде параболы 4 порядка: y=a₀+a₁x+a₂x²+a₃x³+a₄x⁴. Такая парабола содержит 5 коэффициентов, то есть 5 степеней свободы в декартовых координатах. Если записать ее в параметризованной форме, как мы это сделали с кубической параболой, перейдя от (1) к (3), то парабола четвертого порядка будет иметь ровно шесть степеней свободы, что совпадает с числом условий задания 3. То есть мы получим единственное решение. А если оно нас по каким-либо причинам не устроит? Где брать управляющие параметры?

Искомая кривая может быть найдена на основе свойств кремоновых преобразований плоскости с совмещенными F-точками [6]. Этот вариант решения настолько интересен и имеет столько практических приложений, что заслуживает отдельного учебного пособия в рамках курса инженерной графики.                                  

Не будем переходить к кубическим кривым общего вида, не будем повышать порядок, не будем использовать конструктивный аппарат центральных кремоновых инволюций. Возьмем старую добрую параболу (1), но увеличим число интервалов. Введем в рассмотрение промежуточные точки B(x_B, y_B), C(x_C, y_C). Это допускается при условии, что в стыковых точках B, C будет обеспечена гладкость второго порядка. Получаем три дуги AB, BC, CD, каждая из которых описывается уравнением вида (1).

Таким образом, ищем решение в виде:

дуга AB: y=a₁x³+b₁x²+c₁x+d₁ при [x_A, x_B],                                               (18)                                        

дуга BC: y=a₂x³+b₂x²+c₂x+d₂ при [x_B, x_C],                                                (19)                                           

дуга CD: y=a₃x³+b₃x²+c₃x+d₃ при [x_C, x_D].                                                (20)

Обвод (18…19) обладает двенадцатью степенями свободы. Далее мы увидим, что этого достаточно для выполнения задания 3. Управление формой обвода обеспечивается (в небольших пределах) изменением координат x_B, x_C узловых точек B, C.

Для определения неизвестных коэффициентов a_i, b_i, c_i, d_i следует составить 12 уравнений. В эти уравнения войдут как граничные условия в концевых точках A, D, так и условия гладкой стыковки в узлах B, C. При подстановке конкретных числовых значений надо учитывать знак кривизны: в декартовых координатах кривая “выпуклостью вверх” имеет отрицательную кривизну. Приступаем к составлению уравнений.

В точке A имеем:

y_A=a₁x_A³+b₁x_A²+c₁x_A+d₁ ,                                (21)

y′_A=3a₁x_A²+2b₁x_A+c₁ ,                                      (22)

y′′_A=6a₁x_A+2b₁ .                                                (23)

Здесь y_A, y′_A, y′′_A – граничные условия в точке A.

В узловой точке B имеем условия сопряжения участков AB и BC:

y=a₁x_B³+b₁x_B²+c₁x_B+d₁=a₂x_B³+b₂x_B²+c₂x_B+d₂ ,                               (24)

y′=3a₁x_B²+2b₁x_B+c₁=3a₂x_B²+2b₂x_B+c₂ ,                                            (25)

y′′=6a₁x_B+2b₁=6a₂x_B+2b₂ .                                                                (26)

В узловой точке C записываем условия сопряжения участков BC и CD:

y=a₂x_C³+b₂x_C²+c₂x_C+d₂=a₃x_C³+b₃x_C²+c₃x_C+d₃ ,                               (27)

y′=3a₂x_C²+2b₂x_C+c₂=3a₃x_C²+2b₃x_C+c₃ ,                                            (28)

y′′=6a₂x_C+2b₂=6a₃x_C+2b₃ .                                                               (29)

В точке D имеем граничные условия:

y_D=a₃x_D³+b₃x_D²+c₃x_D+d₃ ,                                                                 (30)

y′_D=3a₃x_D²+2b₃x_D+c₃ ,                                                                      (31)

y′′_D=6a₃x_D+2b₃ .                                                                                (32)

Получено ровно двенадцать уравнений (21…32) для определения двенадцати неизвестных коэффициентов a_i, b_i, c_i, d_i в математической модели (18…20) конструируемого трехзвенного обвода ABCD. Для решения СЛАУ (21…32) используем команду lsolve пакета Mathcad. Например, при значениях граничных условий  x_A=y_A=0, x_D=3, y_D=1, y′_A=y′_D=1, y′′_A=-5.656854 (радиус кривизны R_A=0.5, “выпуклостью вверх”), y′′_D=2.828427 (радиус кривизны R_D=1, “выпуклостью вниз”) получен обвод, представленный на рис. 4, б. Найденный обвод, несмотря на свой лихой вид, удовлетворяет всем условиям задания 3. Управлять его формой можно лишь посредством изменения координат x_B, x_C узловых точек.

Заключение

Предлагается ввести в курс инженерной компьютерной графики задание “Плоские обводы”, направленное на изучение элементарных расчетно-геометрических способов моделирования линий с заданными динамическими свойствами. 

Список литературы

1. Иванов Г.С. Начертательная геометрия: учебник для вузов / Г.С. Иванов. – М.: Машиностроение, 1995. – 224 с.

2. Котов И.И. Учебное пособие по начертательной геометрии на базе ЭВМ. Обводы точек на плоскости /Г.С. Иванов, И.И. Котов, В.И. Якунин. - М.:МАИ, 1977. - 53 с.

3. Фокс А. Вычислительная геометрия. Применение в проектировании и на производстве / А. Фокс, М. Пратт. – М.: Мир, 1982. – 304 с.

4. Короткий В.А. Начертательная геометрия: конспект лекций / И. В. Буторина, В.А. Короткий, Л.И. Хмарова. – Челябинск: Издательский центр ЮУрГУ, 2014. – 191 с.

5. Glaeser G. Geometrie und ihre Anwendungen in Kunst, Natur und Technik / G. Glaeser. – Springer Spektrum, 3. Auflage, 2014. – 508 p.

6. Иванов Г.С. Конструирование технических поверхностей / Г.С. Иванов. – М.: Машиностроение, 1987. – 192 с.

Рисунки к докладу

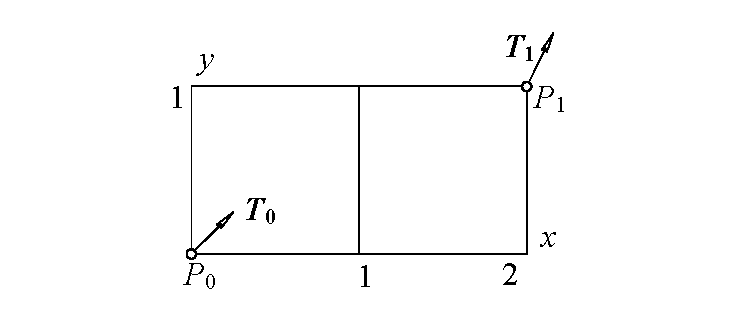
Исходные данные к заданию 1

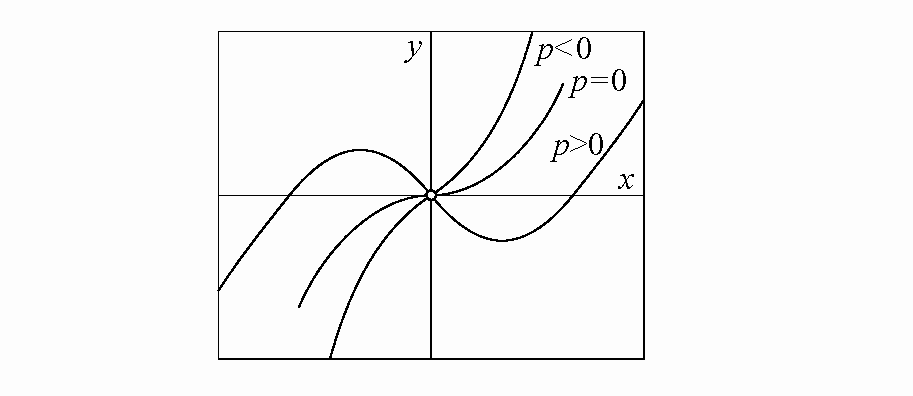
Кубическая парабола

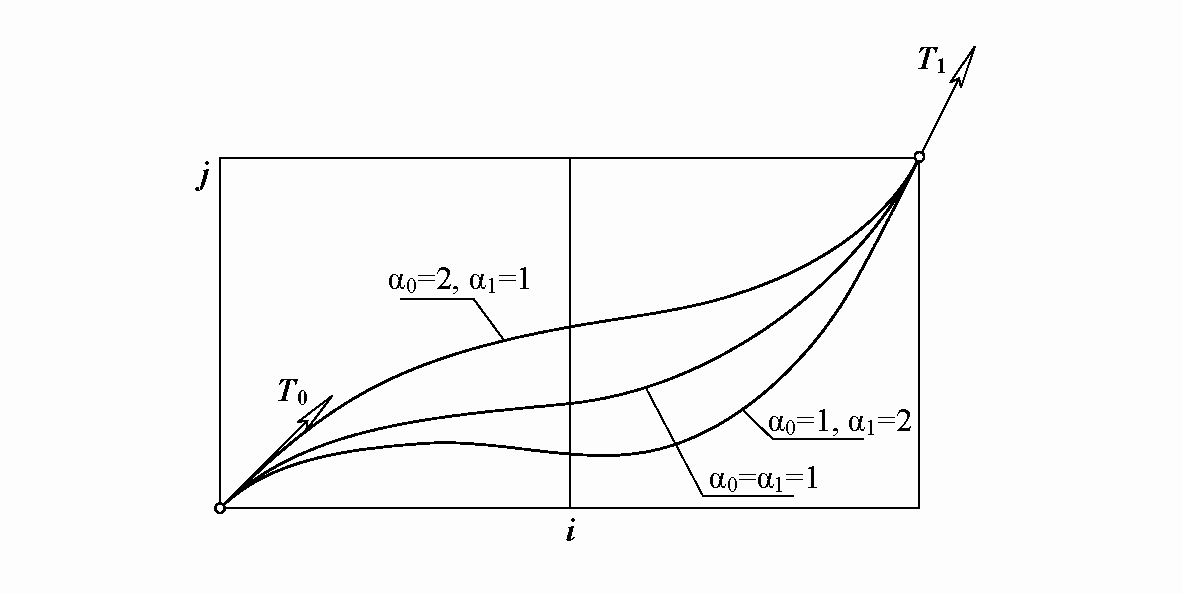
Кривые Эрмита

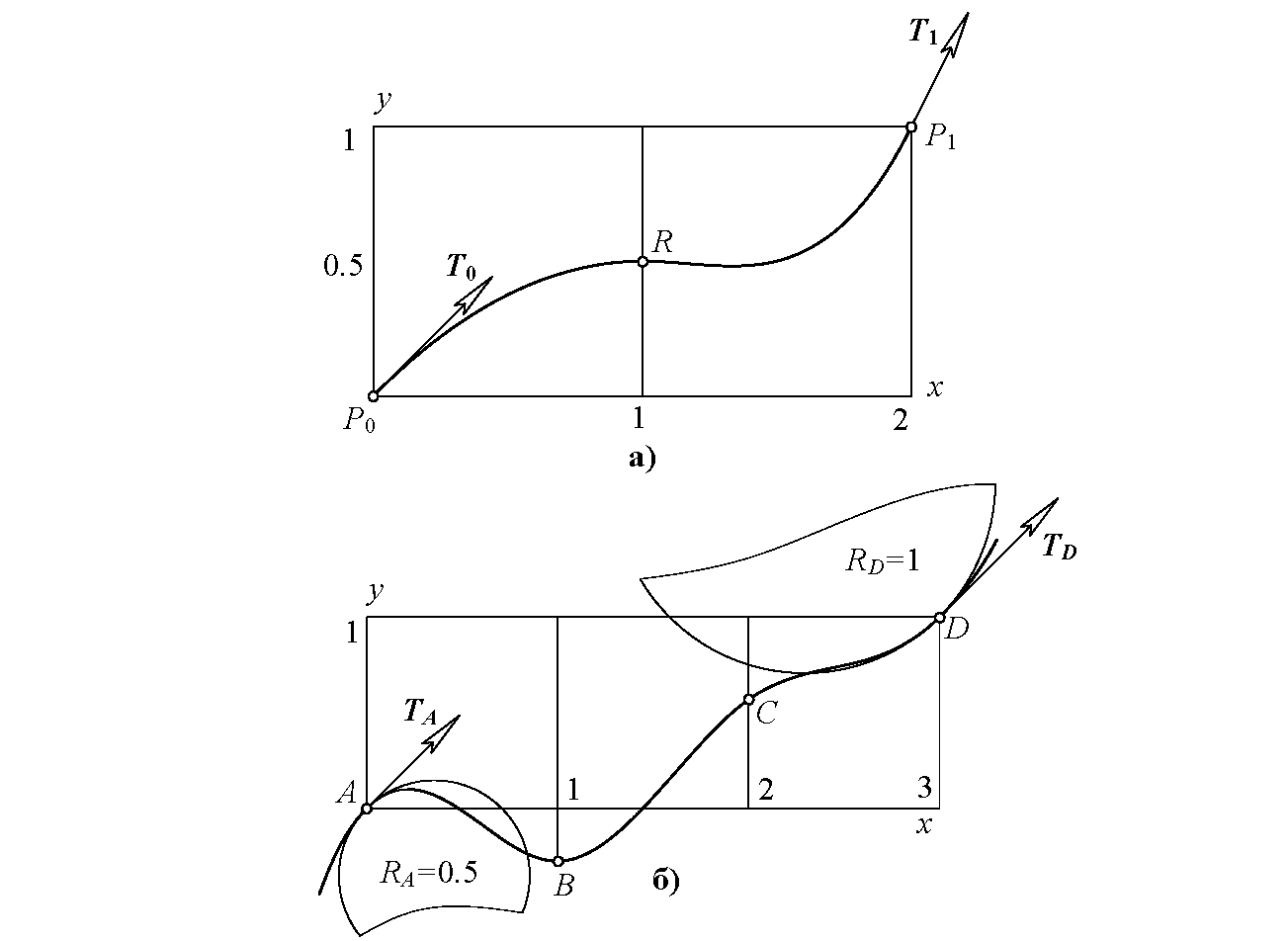
Динамическое сопряжение двух окружностей

Головнин Алексей Алексеевич (14 марта 2017 г. 12:34)	Здравствуйте Виктор Анатольевич и Татьяна Юрьевна! Представляется,  что Ваш доклад мог бы стать предметом рассмотрения на ФПК преподавателей кафедр инженерной графики. Впрочем, неоднократно разными участниками высказывалась мысль, что эта конференция сама выполняет роль ФПК. Очень интересен материал и в качестве идеи лабораторной работы по курсу компьютерной графики, но только после очень большой переработки. Сомнительна идея самой концепции давать такие глубокие знания в учебном курсе инженерной или компьютерной графики для студентов технических специальностей. Не правильнее ли давать крепкую математическую подготовку, а выпускники, для которых работа с таким материалом станет профессией, будут знать, где найти или к кому обратиться за квалифицированной консультацией по рассмотренному Вами вопросу. Отдельная благодарность за информацию об очень интересной иностранной книге. Уважаемые коллеги, привожу работающую ссылку, скачивается сразу без подвохов. http://ru.bookzz.org/book/2355349/8e5642 С уважением Головнин А.А.
Селиверстов Александр Владиславович (14 марта 2017 г. 15:01)	Здравствуйте, Алексей Алексеевич! Книга [Glaeser 2014] действительно хорошая. Спасибо за адрес. Заодно можно вспомнить немецкий язык, на котором в конце 1920-х годов в СССР публиковали статьи по математике, как сейчас на английском. Конечно, например, рисунок на стр. 60 (Abb. 2.30 Seitenriss) - это не совсем то, чему учат в курсе НГ. Не стану перечислять все иллюстрации, но это не только забавные картинки. Кстати, нарисованы и коноиды тоже. Есть красивые иллюстрации минимальных поверхностей. И совсем не вредно, глядя на такие картинки, напомнить, что они иллюстрируют физические законы, хотя дети знакомятся с ними ещё до школы. Иллюстрируется связь с биологией и архитектурой. Эта книга могла бы служить хорошей иллюстрацией к докладу Владимира Игоревича и Николая Андреевича О значении геометрии в технике и науке. Ещё радует, что на стр. 279 используются простые дроби, а не десятичные. Пустяк, но это говорит о понимании авторами проблемы точности вычислений. Ведь именно десятичные дроби, а точнее - используемое при этом округление, служат источником ошибок. С уважением, А.В. Селиверстов
Головнин Алексей Алексеевич (14 марта 2017 г. 16:13)	Здравствуйте Александр Владиславович! Очень внимательно читаю и стараюсь изучать все материалы конференции. Ваши короткие и четкие комментарии к докладам для меня всегда бывают очень полезными и информативными. Ваше первое впечатление от книги воспринимаю как приглашение к более подробному изучению. Надеюсь, авторы не будут в обиде за наше с Вами общение на их площадке. С уважением Головнин А.А.