2. ИНЖЕНЕРНАЯ ГЕОМЕТРИЯ В ОБРАЗОВАТЕЛЬНОМ КОНТЕКСТЕ. ФУНКЦИОНАЛЬНЫЙ ПОДХОД

В рамках авторского видения сути и содержания инженерной геометрии как составляющей начальной инженерной подготовки и ГГП дан обзор её основных фрагментов в этом контексте. В частности, предлагается методически опираться на аналогию детали в качестве функционального “конструктивного слова” и слова как первичного носителя смысла естественного языка.

Продолжая тему первой публикации, постараемся подкрепить свою точку зрения дополнительными аргументами. При этом позволим себе небольшие повторения ради непрерывности изложения и чтобы не затруднять чтение ссылками.

… Одним из направлений предлагаемой адаптации традиционного содержания курсов ГГП к современным реалиям являются ранее сформулированные коллегами предложения о коррекции части традиционных положений и методов ГГП, в том числе в рамках НГ, условно в виде курса инженерной геометрии. Естественно, что содержание, скорректированное и обогащенное теми или иными инженерным акцентами, не все видят одинаково. Можно рассматривать и более кардинальные перспективы [1]. Суть и содержание корректировок могут трактоваться с разных точек зрения. Например, опираясь на фундаментальную роль математики в инженерии, есть предложения и конкретные разработки по переходу на позиции инженерной геометрии, соединяя геометро-графический анализ и аналитические описания геометрических и псевдогеометрических образов, на основе символических методов, корректируя, в частности, и содержание НГ [2, 3,4]

Мы же вкладываем в понимания сути и содержания “инженерной геометрии” другое. Действительно, какое бы прилагательное не предшествовало существительному геометрия – она в любом случае остается, в первую очередь, геометрией. Подразумеваем здесь только “евклидову”, в рамках ГГП, и её отображения в декартовой системе. Та или иная специфика изложения геометрии, её связи с определенными объектами, целями, задачами, методами отображения и т.д. определяется уточняющими прилагательными. Содержание и методы именно “инженерной геометрии” в образовательном контексте, как полагаем, должны быть направлены на приобретение знаний, навыков и умений для описания и преобразования геометрических характеристик объектов и их моделей, которые по определению функциональны. Именно этим они непосредственно связаны с искусственными объектами “инженерного происхождения”. Аналогично, как специфическая сфера приложения геометрического анализа, в [5] рассматривается “геометрия живого”, которую можно было бы назвать и геометрией живой природы или неинженерной геометрией.

Трактовка инженерной геометрии как “геометрии для инженера” в указанном контексте ничего не меняет. Аналогично можно говорить и о геометрии в рамках академической математической подготовки, что определяет специфические подходы к ней. Там, конечно, область и её специальных приложений, в том числе в рамках начертательной геометрии.

Когда мы говорим студентам о сути начертательной геометрии, имеем в виду не “другую” геометрию, а совокупность положений и методов графического описания геометрических объектов и отношений между ними на основе проекционных изображений и их систем. Устойчивое сочетание “аналитическая геометрия” по сути выделяет в аналитических методах и формах математических уравнений те, которые описывают геометрические образы. Начертательная геометрия и аналитическая геометрия конечно не отдельные геометрии, а теории отображения геометрических объектов и отношений между ними – отображения соответственно на основе “начертания” проекций и их систем или в виде тех или иных аналитических уравнений для последующего анализа и (или) синтеза путем их преобразований. Их методы при решении конкретно поставленных задач могут применяться отдельно или совместно.

В свою очередь, “многомерная геометрия”, образно говоря, взаимный “геометрический реверанс” аналитике, который позволяет распространить геометрические образы и термины по отношению к реальному пространству на структурно подобные уравнения аналитической геометрии с переменными более трех. А при понижении их мерности вернуться на “круги своя” - например от гиперсферы к “привычной и понятной” сфере, знакомой по визуализации в декартовых координатах. Только зачем и ради чего, сначала ненаглядная гипер? Но привлечение “понятных, осязаемых и наблюдаемых” двух, одно и нуль мерных пространств методически удобно для пояснения логики простановки размеров с геометрических позиций, в частности, при пояснении отсутствия ряда размеров “по умолчанию”[14].

Многомерные “пространства” - подобные терминологические и геометрические аналогии для описании зависимостей, в которых часть или даже все переменные (которых более 3-х) могут иметь размерности, не связанные с пространственной протяженностью (при этом они, как правило, нормализуются). И, например, “точка”, как одно из геометрических понятий, в этом “многомерном пространстве состояний”, есть терминологическая фиксация некого набора значений этих переменных.

Или еще, в порядке аналогии, пример. Известна научно–прикладная область “Статистическая радиотехника”. Объекты и процессы этой инженерной области те же – радиотехнические. А вот аппарат математического анализа и синтеза этих устройств и процессов при этом специфичен. Это теория вероятностей и математическая статистика, описывающие на своем красивом и емком языке  стахостические процессы в радиосистемах.

… Современные средства отображения информации о технических объектах, в частности, их геометрии, – основном “вместилище” функциональных характеристик деталей, сборочных единиц и их параметров – не вчера поставили вопрос о дальнейшей роли и месте традиционных технологий и средств инженерной графики. Главное – цифровые компьютерные геометрические 3D модели гибки и динамичны, так же как и их “проекционная” визуализация на мониторе. И, несмотря на пока двумерное представление, позволяют сделать заметно более эффективным процесс всестороннего геометрического анализа и преобразования моделей прототипов технических объектов, причем в “реальном времени”. Другими словами,  они более эффективное и естественное средство для первичного анализа геометрии ТО, на основе ЭМИ. По отношению к ним, система 2D изображений (тоже 3D модель) для отображения трехмерных объектов, как на твердых носителях, так и в электронном виде, менее гибка. Её разрешающая способность в целом ниже, а адекватное восприятие дается не просто. Об этом упоминал и сам Г. Монж, и это не надо забывать, цитируя классика. Твердотельные модели на основе 3D принтеров для широкого применения пока еще дороги и не так мобильны, голографические представления не до конца отработаны для массового применения. Уже реальна графика на “электронной бумаге” как на мониторе, триплексные прозрачные панели с жидкокристаллической матрицей, позволяющей реализовать тактильный интерфейс при формировании изображений.

Собственно научное содержание и значение НГ вообще не может быть предметом обсуждения, особенно в контексте “быть или не быть”. Проекционные методы их роль сохранятся, в том числе, в образовательном аспекте. Они элемент формирования зрительных представлений, сопровождают визуальный обзор и анализ окружающей среды со множеством технических объектов, входят в состав других технологий представления зрительной информации. Её анализ во многих случаях более продуктивен на основе необходимых представлений о закономерностях проекционных изображений и их систем. В составе конструкторской документации проекционные чертежи еще не потеряли, но постепенно теряют свое значение. Вышесказанное актуально не для задач синтеза, а по отношению к задачам анализа. Например, “театр теней” на поверхностях окружающей среды является, и всегда будет являться, информационным дополнением к непосредственно наблюдаемым объектам. Благодаря этим естественным проекциям существенно дополняется восприятие геометрической формы и её положения в пространстве, как в статике, так и динамике. Отображение пространственных объектов и их отношений методами классической начертательной геометрии, предполагает непростые модели. У них есть своя ниша в общей иерархии моделей отображения. Эти модели и методы конечно развивают пространственные представления, но разве только они и лучшим ли образом? 3D модели развивают его не хуже. Это ведь как ставить задачу. Допустим, надо описать геометрию объекта вербально, а затем синтезировать его образ в виде 3D электронной модели. Чем это хуже для развития пространственных представлений?

Процесс адаптации к новым условиям традиционных курсов графо-геометрической подготовки в России не прост. Это определяется наличием большого количества отработанных методик, учебной и методической литературы на основе традиционной парадигмы, естественной инерции позиций части преподавателей. Но медленнее, чем необходимо, реализуются не столько технологические, сколько новые содержательные возможности ГГП на основе КГ и других информационных технологий.

Геометрическая форма как одна из основных характеристик технических объектов (деталей и сборочных единиц) исходно функциональна. И её функцию можно трактовать как совокупность типовых инвариантных составляющих, которые определяют её в разной степени в целом и в разной степени определяют состав и параметры отдельных поверхностей. Эти обобщенные составляющие такие: рабочая (инструментальная), адаптивная (приспособления к другим деталям и среде, в том числе человеку); технологическая (как “ответ” на технологию формообразования); интегрирующая (связанная с учетом требований унификации, конструкторских традиций и т.п.). Пример такого функционально-геометрического анализа с позиций инженерной геометрии показан на рис 1. Кроме этих обобщений рационально привлекать и элементарные функции (операции) Коллера [6,8].

Можно говорить, что деталь и её геометрия являются минимальными носителями функционально-конструктивного “смысла”, аналогично тому, как слово естественного языка есть его основная смысловая единица. Эта аналогия позволяет подчеркнуть методологически и методически противоречивое обстоятельство. Словарь и другие составляющие естественного устного и письменного языка обучаемого изучался и совершенствуется на сугубо смысловом (функциональном) начале слова, в отличие от традиционной методики изучения геометрической основы начальной инженерной подготовки, оперирующей отвлеченными геометрическими образами.

И на этом пути после “функционального начала” естественна методика анализа сборочных единиц как высказываний и текстов и на этой основе формирование представлений о специфическом функциональном геометрическом языке и его категориях: алфавите, словаре, грамматике, синтаксисе и т.д.

Несколько утрируя, заметим, что с этих позиций традиционный – нефункциональный – подход к геометрии технических объектов на начальной стадии инженерной подготовки аналогичен чтению или сочинению “бессодержательных” текстов при изучении родного языка общения. Анализ морфологической аналогии детали и слова как минимальных функционально–содержательных единиц, высказываний, текстов на конструктивном и естественном языке и более глубоких аналогии в этой плоскости предполагают отдельное рассмотрение.

При отвлеченном геометрическом анализе форма остается как бы функционально “пустой”, и это не помогает, в таком подходе, полноте восприятия и самой геометрии модели. Понимаем, что это некий антитезис традиционным постулатам ГГП – чисто геометрическому анализу и последующему отображению геометрии технических объектов. Но ведь современная системная ситуация, трансформированная парадигма инженерного образования, доступные технологии моделирования и графики тоже другие, о чем мы уже упоминали ранее. Сразу заметим, что не имеем в виду на начальной стадии ГГП подробный конструктивный или технологический анализ геометрии детали или её моделей. Имеется в виду уровень функциональной пропедевтики, когда геометрия объекта может быть связана с простыми или обобщенными функциями, утвердившимися за деталями простой формы и их несложными комбинациями.

Ниже покажем, что имеем в виду под переходом с геометрического языка (который остается первичным, иначе это геометрия) на функциональный при описании геометрических задач прикладного характера. Речь идет не об обычных эпизодических иллюстрациях, а методическом подходе, предполагающем опору на устойчивые связи данной геометрической поверхности с её конструктивными функциями, определяющими образ детали, выделяющей её по этому признаку среди других. В чистом виде геометрическая поверхность как таковая, физическую функцию выполнять не может. Поэтому речь может идти о геометрической форме, в которой данная поверхность определяет главную функцию (определяет главный признак) детали, не исключая других поверхностей для образования замкнутого объема детали и выполняющих вторичную роль (функцию).

Не имея здесь цели провести исчерпывающий анализ устойчивых связей геометрических поверхностей и их композиций с их конструктивными функциями, ограничимся короткой иллюстрацией на примере цилиндрической поверхности и плоскостей. В составе слова базовую смысловую нагрузку несет корень слова. Как и слово естественного языка, геометрическая форма детали имеет основную функционально–конструктивную геометрическую составляющую, – аналог корня в слове. Более конкретный смысл слова определяется текстом и контекстом и аналогично функция детали – в составе сборочной единицы.

На рис.2 приведены эскизы простейших деталей, для которых устойчивый функциональный образ определяется базовой цилиндрической поверхностью (для деталей вращения) и плоскостями и только плоскостями для гранных форм. Кроме характера поверхности функциональный образ этих деталей определяется и отношением параметров формы поверхности и размеров их отсеков. Заметим, что здесь функциональные наименования даны вне конструктивного текста (т.е. вне сборочной единицы). Как и в естественном языке смысл слова уточняется контекстом и прилагательным, так и функция детали на основе данной поверхности уточняется в контексте СЕ. При этом первичная форма детали обогащается геометрическими элементами, образуя аналоги морфем слова “приставки”, “суффиксы” и “окончания”. Так, уточняющей функцией валика могут быть “прижимной” или “опорный”, при этом в детали появятся и вторичные геометрические элементы. Как и смыслы слов естественного языка, нюансы функционального геометрического образа детали зависят не только от параметров формы, но и взаимного положения по отношению к другим “конструктивным словам” и их положения в пространстве.

Изменение функционального содержания геометрии детали или её модели при изменении отношений параметров формы и параметров их взаимного положения её составляющих предполагает совместный анализ и последующий синтез этих описательных признаков (формы и параметров). Это хорошо согласуется с практикой определения достаточной совокупности видов модели (например на чертеже), на которую влияет состав размерной категории, содержащей условные обозначения ряда поверхностей.

Если элементный состав геометрии детали и отношение параметров определяет её функциональный образ, то абсолютные размеры важны для формирования у обучаемых правильных масштабных представлений между моделью и моделируемым объектом. Масштабные категории непременно должны сопутствовать любым отображениям модели и акцентироваться.

Ненатуральный масштаб изображения искажает представления студента о “значимости” геометрии и функциональной нагрузке изображаемого узла. Изображение отображается и остается в его сознании без масштабной коррекции. Часто ценность собственно изображения, выполненного студентом, не так уж невелика. Оно может быть почерпнуто из соответствующих баз данных, а вот представленный в системной форме фрагмент имеет уже гораздо большее образовательное значение в рамках “инженерной геометрии”.

….Надо стимулировать обучающихся постоянно наблюдать, анализировать и систематизировать геометрию механизмов, машин и сооружений в бытовой, открытой пространственной и производственной средах и затем ставить перед ними задачу её устного, текстового описания, а затем графического, в виде наброска, рисунка. Даже держа в руках учебную модель студент должен иметь привычку тактильно оценивать макро и микрогеометрию её поверхностей, зафиксировать и оценить её вес в некой связи с геометрическим объемом и т.д.

Это основа для иллюстрации и освоения первичных навыков и сути важнейшего в инженерной и научной деятельности процесса моделирования, в частности геометрической формы. Геометрическое моделирование мысленного или реального объекта, в своей первичной цели и главном содержании, означает описание его геометрии с заданной целью при заданных ограничениях и условиях. Именно переход от реальной или мысленной формы к геометрической модели (в любой форме) с данной целью при данных условиях и ограничениях есть важнейший элемент инженерного искусства и, естественно, в рамках геометро–геометрической подготовки. В зависимости от постановки задачи привлекается та или иная модель геометрии и отображается тем или иным способом (текстом, рисунком, чертежом, ЭМИ, скульптурно..). Для примера реализации задания собственно на моделирование внешней формы шуруповерта рис.3a, её модель в рамках условий и ограничений (модель должна быть гранной), представлена 3D моделью рис.3в и проекционным чертежом на рис. 3б.

Для сравнительной оценки “разрешающей способности” такого представления, надо оценить проблемы, которые возникнут, если надо приблизить форму этой модели, как первичного замысла, к форме на рис 3а, сохраняя проекционный чертеж для отображения её внешней поверхности и задания параметров …

Даже в рамках традиционных сочетаний простых геометрических форм в задачах на пересечение поверхностей полезно трактовать их, пусть как грубые, но модели, оболочек, корпусов и т.д., указывая это в основной надписи по “форме 1”, снабжая квалификационной характеристикой и указанием модельного материала. C позиций инженерной геометрии и отображения её объектов нецелесообразны, практически ничего не дающие упрощения, в виде учебных основных надписей, расположения на одном формате или файле, задач относительно разных объектов. В порядке элементов инженерной культуры здесь должна простая формула: один объект (достаточные изображения и параметры) – один формат или файл, – одна основная надпись, – соответствующие атрибуты, предусмотренные для указания в спецификациях. Эти же требования относятся к заданиям, которые должны быть параметрически определены как соответствующие модели, а не “размерами для вычерчивания”.

“Инженерную геометрию“, мы рассматриваем как составляющую начальной стадии инженерной подготовки, оперирующую метрически определенными функциональными прообразами совокупностей геометрических поверхностей, образами деталей и сборочных единиц технических объектов, их соответствующими моделями и различными отображениями. Эти отображения по форме могут быть устными, письменными, графическими – на твердых или электронных носителях, в скульптурной форме. При этом формулировка геометрических задач в связи с их функциональным содержанием предполагается в прикладных формулировках. Такой подход естественным образом стимулирует выделение практически значимых задач, непосредственно направленных на формирование деятельностных инженерных компетенций. При этом интегрируются элементы графо-геометрической и проектно-конструкторской подготовки и первичные знания предметной области будущего специалиста. Конечно, прикладные формулировки геометрических задач не являются каким–то откровением в разнообразной методической практике ГГП. Мы хотим сделать акцент на продуктивность такого подхода как систематического на начальных стадиях инженерной подготовки и обратить внимание на возможность обобщения понятий и методов в рамках информационных языков, одним из которых является геометрический.

Предвидим вопрос, связанный с необходимостью анализа и решения собственно геометрических задач как отдельной дисциплины в их академических постановках, в частности для развития методов НГ и алгоритмов КГ. Такие задачи естественны для творческой работы преподавателей в исследовательском и методическом аспектах. А новые результаты такой работы в прикладных формулировках могут пополнить учебную практику.

Важнейшим в инженерном аспекте является формирование представлений о связи геометрических параметров и нагрузочных способностях элементов деталей. При этом геометрия детали и её параметры приобретают функциональный смысл в контексте его реализуемости, а не как номинальной формы. Геометрия, никак не привязанная к физическим ощущениям или характеристикам, их уровню и масштабу, остается у обучаемого абстракцией, плохо закрепленной в сознании.

… Например, известна классическая учебная работа выполнения фрагментов сборочных чертежей или электронных моделей резьбовых соединений с помощью стандартных крепежных деталей. По опыту знаем, что если попросить студенческую аудиторию оценить усилие сжатия деталей, которое можно обеспечить до разрыва стержня, если стержень (болта, винта, шпильки) по заданию например D=16мм, то оценки будут в десятки раз занижены, по отношению к допустимым усилиям. Достаточно трех минут (оценка элементарна), чтобы закрепить образное представление о масштабах геометрических величин, определяющих её работоспособность (рис.4). Все приведенные фрагменты и точки зрения реализуются, в преподавательской практике авторов, к сожалению, не всегда системно и частично излагались ранее [1,8, 9,12,13].

Функциональные подходы на начальных стадиях ГГП, могут поддержать потребность в ней как отдельной области подготовки, и как фактор формирования инженерной ментальности. Но в практике ведущих технических университетов мира таковой уже практически нет… Она интегрирована с задачами других дисциплин и решается на их основе.

Представляется, что в контексте изложенной здесь трактовки инженерной геометрии продуктивны, заданные параметрически или геометрическими условиями, постановки и решения геометрических задач в среде AUTOСАD, представляемые А.Л. Хейфецем [10]. Критика его авторской позиции, на наш взгляд, связана не столько с её сутью, сколько в сравнении с другими постановками (формулировками) задач, а именно задачами поиска геометрических закономерностей, что не одно и тоже [11,2]. При поиске геометрических закономерностей первична логика, а точность графической интерпретации вторична. При индуктивном пути к истине точность реализации геометрических условий первична и, при определенных условиях, позволяет делать логические выводы и выдвигать гипотезы. Кроме того, в арсенале доказательных научных методов, как известно, дедуктивные и индуктивные методы равноправны. И каждые основаны на своей логике, предполагая её корректное применение. Поэтому противопоставления в этой плоскости, особенно с позиций перехода к инженерной геометрии, вряд ли логичны и продуктивны.

Можно говорить шире о необходимости модернизации и моделях содержания начальной стадии инженерной подготовки вообще. Информационные технологии позволяют ставить вопрос о консолидации актуальных элементов традиционного содержания ГГП и возможностей усиления междисциплинарного взаимодействия в рамках инженерной пропедевтики. Как вариант такой пропедевтики на основе базовых понятий, умений и навыков могут составить такие, инвариантные для направлений подготовки, разделы:

1. История техники (логика развития техносферы).
2. Технические объекты и процессы. Инвариантная структура описания.
3. Современные технологии формообразования (обзор).

При этом графические средства будут сначала выступать как эффективные носители информации, а затем как предмет освоения их технологий.

Список литературы

1. Лепаров М.Н. Инженерная графика: To be or not to be?/ М.Н. Лепаров, М.Х. Попов // Проблемы качества графической подготовки студентов в техническом вузе в условиях ФГОС ВПО ” Сборник статей.– Пермь: Изд-во ПНИПУ, 2012. – С.85-93.

2. Иванов Г.С. Предыстория и предпосылки трансформации начертательной геометрии в инженерную / Г.С. Иванов // Геометрия и графика,Т.4, Вып.2, 2016. C.29 –36.

3. Кайгородцева Н.В. Инновационая методология начертательной геометрии / Н.В. Кайгородцева. – Омск: ОмГТУ, 2013. –184с.

4. Соколова Л.С. Геометрическая подготовка бакалавров в современных условиях / Л.С. Соколова // VI международная интернет-конференция “Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации” Сборник статей. – Пермь: Изд-во ПНИПУ, 2016. С. 326–333.

5. Иваницкий Г.Р. Геометрия живого / Г.Р. Иваницкий, В.П.Гартштейн. М:, Издательство “Знание”, 1971. –32с.

6. Половинкин А.И. Инженерное проектирование./ А.И. Половинкин М.; Машиностроение. С.–Петербург. Изд-во Лань,2017. – С.364

7. Взятышев В.Ф. Введение в методологию инновационной деятельности/ В.Ф. Взятышев / Учебное пособие. М:, Изд-во “ Европейский центр по качеству “ 82с.

8. Лепаров М.Н. Основы инженерного проектирования/ М.Н.Лепаров, М.Д.Вичева,М.Т.Георгиев/ Cофия: изд-во СОФТРЕЙД, 2008. – 356с.

9. Горнов А.О. От 3D модели сборочной единицы к чертежу детали./ А.О. Горнов, А.Д. Козырев // VI международная интернет-конференция “Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации” Сборник статей.- Пермь: Изд-во ПНИПУ, 2016. – С. 476-490.

10. Хейфец А.Л. Геометрическая точность компьютерных алгоритмов конструктивных задач / А.Л. Хейфец // VI международная интернет-конференция “Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации” Сборник статей.- Пермь: Изд-во ПНИПУ, 2016. С. 367 –388.

11. Сальков Н.А. Начертательная геометрия – база для компьютерной графики / Н.А.Сальков // Геометрия и графика: Научно–методический журнал. Т4, вып.2 , 2016. С.37 – 47.

12. Горнов А.О. Практическая часть модифицированного курса “ Теория построения чертежа/ А.О. Горнов, А.Ю. Губарев, Л.В. Захарова // Сборник материалов 3-ой Международной научно-практической интернет–конференции «Проблемы качества графической подготовки студентов в техническом вузе в условиях перехода на образовательные стандарты нового поколения». Пермь: Изд-во ПНИПУ, 2012. С.139 – 148.

13. Горнов А.О. Пример междисциплинарной интеграции курса инженерной графики / А.О. Горнов, Е.М. Логинова. Проблемы качества графической подготовки студентов в техническом вузе в условиях ФГОС ВПО: материалы IV Международной научно-практической интернет – конференции. - Пермь: Изд-во ПНИПУ, 2014.С.199 – 209.

14. Горнов А.О. Основания для алгоритмизации простановки размеров на чертежах / А.О. Горнов, А.Ю. Губарев, Захарова Л.В. Труды конференции “ Информационные средства и технологии”– М.; Издательство МЭИ, 2008. –230с.

Рисунки к докладу

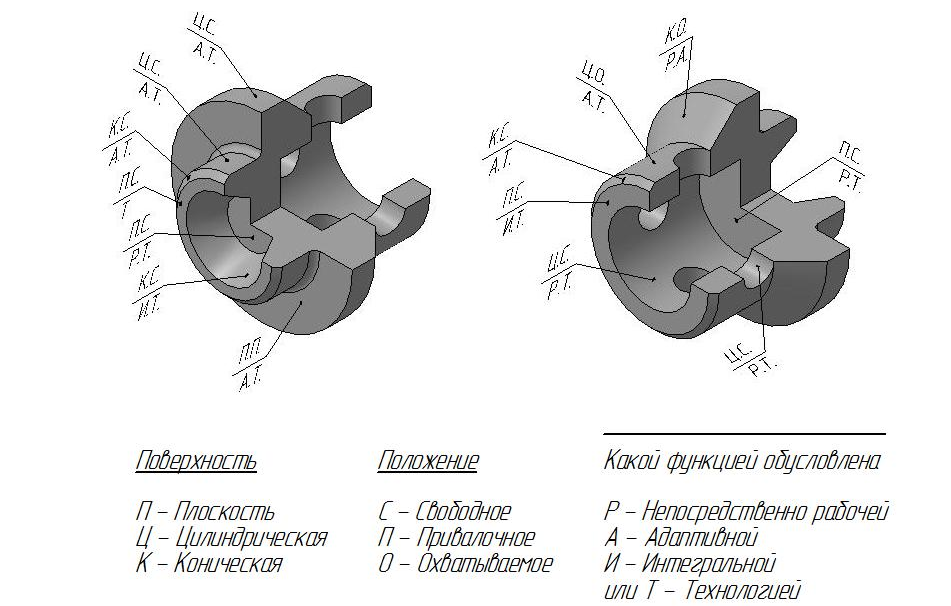
Пример функционально–геометрического анализа клапана на основе инвариантных составляющих функций поверхностей деталей

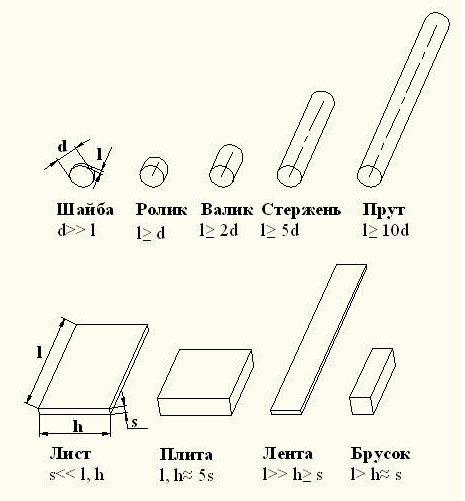
Эскизы простейших деталей–заготовок и их функциональные названия в зависимости от соотношения параметров

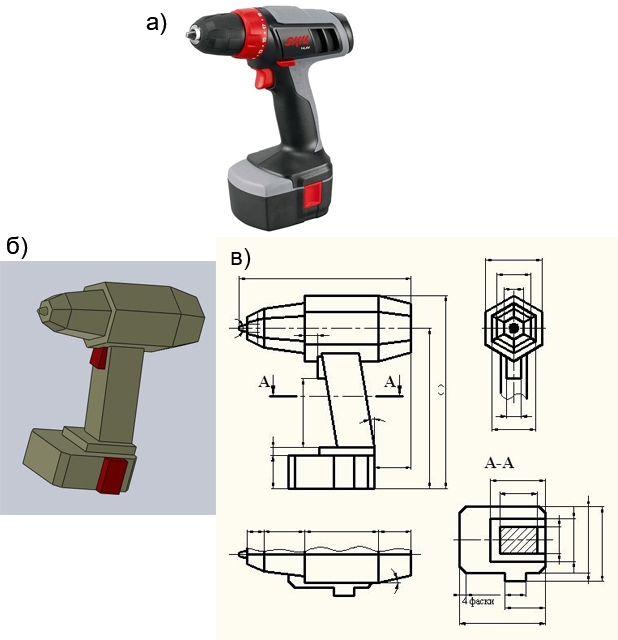
Пример моделирования внешней формы технического объекта при заданных условиях и проекционный чертеж модели

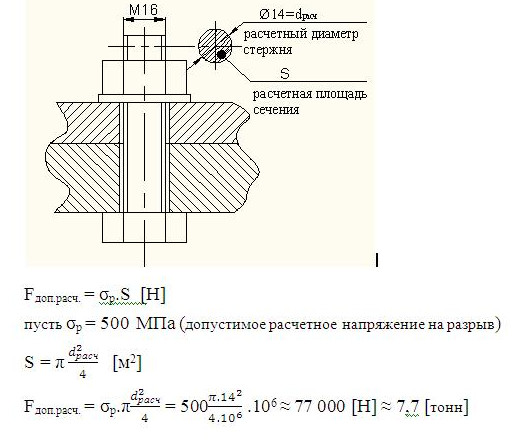
Пример элементарной оценки характеристики работоспособности стержня болта, связанной с параметром геометрии

Тихонов-Бугров Дмитрий Евгеньевич (26 марта 2017 г. 0:44)	Уважаемые авторы! Интересно Ваше мнение: указанные направления подготовки (разделы) д.б. присущи междисциплинарному курсу? В таком случае, какой раздел (кроме последнего) приходится на долю кафедры с названием, соответствующим спец. 05.01.01.? Или это вариант того, о чём писал уважаемый Михаил Николаевич в статье 1 - курс, который должны взять на себя нынешние кафедры для того, чтобы выжить?   С уважением, Тихонов-Бугров.
Горнов Александр Олегович (26 марта 2017 г. 13:01)	Уважаемый Дмитрий Евгеньевич, здравствуйте! Если мы правильно поняли,  Ваш вопрос относится к указанным в конце второй статьи разделов инвариантов инженерной пропедевтики.  Немножко поясним  это предложение. Пропедевтику мы трактуем на  основе и уровне “образов черных ящиков ”, когда обсуждаютcя их  ‘’входы и выходы’  , оставляя студенту “интригу” более подробного содержания,  поддерживая интерес и  мотивацию  к  последующим  дисциплинам. Собственно инвариантность относится,  конечно,  к логике развития техносферы, методам описания, анализа и синтеза технических объектов, принципов и средств  современных технологий и проектно-конструкторской деятельности. Предметная иллюстрация по направлениям подготовки. Все это внешне похоже, на некогда бывшие в моде введения в специальность, но более инвариантно.  Относительно кафедральной принадлежности разделов (кому что)   особо не задумывались. Последние, конечно,  за кафедрами ИГ (в современном виде). Основой для предпоследнего раздела о ГСПИ могут быть известные разработки и  результаты Е.В.Усановой. Относительно цели пропедевтики и альтернативы [1] от Михаила Николаевича Вы правильно предположили. Все это   может рассматриваться в контексте “завязывания” междисциплинарных связей, усиления позиций кафедр ИГ в  инженерной подготовке. Но по каждому ТУ это конечно индивидуально и об этом тоже “в голову не брали”.  Фрагментарный опыт был и в МЭИ и Софийском ТУ на основе курсов основ инженерного проектирования. Но в те времена знаниево - дисциплинарная позиция была намного сильней проектно – деятельностной, -  сегодняшней.  К сожалению,   в современных “экономических” подходах к формированию ОПОП и штатов ППС вообще не ясно, какое содержание и  какие связи, кому актуальны, о чем мы здесь частенько  упоминаем. С уважением, А.О., М.Н.
Тихонов-Бугров Дмитрий Евгеньевич (26 марта 2017 г. 13:45)	Уважаемые Александр Олегович и Михаил Николаевич, здравствуйте. Спасибо за исчерпывающий ответ. Всегда хочется конкретики. К сожалению, оптимизма в свете последней фразы, не прибавилось.   С уважением, Тихонов-Бугров.