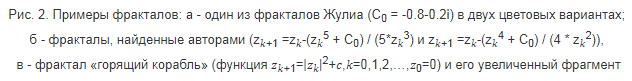О СОЗДАНИИ ФРАКТАЛЬНЫХ ОБРАЗОВ ДЛЯ ДИЗАЙНА И ПОЛИГРАФИИ И НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ ОБОБЩЕНИЯХ, СВЯЗАННЫХ С НИМИ

В работе рассматриваются модификации фракталов Мандельброта и Жулиа. Предлагается интерпретация полученных алгоритмов создания фрактальных образов с позиций многомерной геометрии, что позволяет обобщить отдельные фракталы как сечения общего многомерного гиперфрактала. Предлагаются способы создания новых фрактальных образов как различных плоских и неплоских сечений гиперфрактала, а также на основе сложения гиперфракталов. Предложенные способы могут быть использованы для создания фрактальных образов (плоских и трехмерных) для дизайна и полиграфии.

Введение
В предисловии к книге [1], первое издание которой было выпущено в 1986 году, авторы с удивлением отмечали, что брошюра, в которую авторы включили каталог полученных ими фрактальных образов, «приобрела значительно большую популярность, чем любая из наших чисто научных публикаций». В настоящее время фрактальные образы находят самое широкое применение в различных областях промышленного дизайна, текстильной промышленности, строительной индустрии, полиграфии, пользуются популярностью выставки картин, фресок, витражей, созданных при помощи фрактальной графики [2-6]. На рис. 1 представлены примеры обложек научных изданий (© издательство «Прогресс-Традиция») и школьных тетрадей (© pzbm.ru), на которых используются фрактальные образы. Сказанное позволяет сделать вывод об актуальности разработки способов создания новых фрактальных образов, которые могли бы применяться в дизайне и полиграфии.

В настоящей работе предлагаются способы создания фрактальных образов на основе алгебраических фракталов.

Рис. 1. Применение фрактальных изображений в полиграфии

Алгебраические фрактальные алгоритмы
Понятие фрактал (дробный) введено Б. Мандельбротом в 1975 году как ключевое понятие новой геометрии, элементами которой являются самоподобные структуры. Фракталы принято разделять на геометрические, стохастические и алгебраические [7]. Алгебраические фракталы создаются на основе итерационного вычисления значения некоторой функции, как правило, комплексного переменного. Пусть задана функция комплексного переменного F(z) и рассматривается ее поведение в цепи последовательных итераций: F(...(F(F(z₀)))). Очевидно, результат вычислений полностью определяется начальным положением точки, то есть значением z₀. Последовательность значений, которые принимает функция в этой цепи вычислений, называют орбитой точки z₀. Значение функции при бесконечном числе итераций может: а) стремиться к некоторому значению z_∞ (точка притяжения), б) стремиться к бесконечности, в) изменяться с некоторым периодом, г) изменяться случайным образом.
Тким образом, алгебраические фракталы позволяют описывать нелинейные процессы с обратной связью [1, 7].
Заполняющим множеством Жулиа называют множество точек z₀, орбиты которых ограничены. Если ввести в функцию F кроме переменной z некоторую константу C, тогда результат вычислений окажется в зависимости также и от значения константы.
Множеством Мандельброта называют множество таких точек C₀, при которых орбиты нулевой точки ограничены.
Границы множеств Жулиа и Мандельброта сильно изрезаны, по мере увеличения выбранных фрагментов становятся видны новые детали и подробности, причем характерно появление повторяющихся структур (подобие частей целому). В математике представляют интерес свойства этих множеств, особенности орбит тех или иных точек и образуемые ими области, при этом требуются вычисления очень высокой точности и множества итераций. В задачах дизайна точность производимых вычислений определяется размерами создаваемого изображения в пикселах, каждому пикселу соответствует единственная точка комплексной плоскости.
Дискретная (растровая) модель алгебраического фрактала представляет собой двухмерную матрицу элементов, содержащих информацию о цвете пиксела, столбцы и строки которой соответствуют узлам дискретной сетки, с заданным шагом покрывающей выбранный отсек комплексной плоскости, а цвет пиксела некоторым образом кодирует результаты итерационного процесса. При этом растровая модель является всегда образом множества Жулиа или Мандельброта лишь «с некоторого отдаления», поскольку при увеличении областей вблизи границы этих множеств картина может самым неожиданным образом изменяться.
Известны следующие способы создания фрактальных образов, которые могут применяться в полиграфии и дизайне:
1) поиск подходящего способа раскрашивания точек в зависимости от того, к какому классу они относятся, числа итераций до притяжения к точке или бесконечности и т.п. (рис. 2, а);
2) поиск подходящей функции F, поскольку для каждой функции характерно свое множество Жулиа или Мандельброта и, соответственно, свои визуальные образы (рис. 2, б);
3) выбор подходящего фрагмента множества, поскольку при увеличении отдельных фрагментов изображение заметно меняется, становятся доступны новые, ранее невидимые элементы (рис. 2, в).

Рис. 2. Примеры фракталов: а - один из фракталов Жулиа (C₀ = ...) в двух цветовых вариантах; 
б - фракталы, найденные авторами (F(z) = ... и F (z) = ....), 
в - фрактал «горящий корабль» (функция F(z) = ...) и его увеличенный фрагмент

Отметим, что между фракталами Мандельброта (ФМ) и Жулиа (ФЖ) для одного вида функции F(z) имеется тесная связь: каждая точка ФМ соответствует однократному запуску алгоритма ФЖ с заданной константой C₀ для некоторой начальной точки z₀, а все точки в совокупности являются своеобразным «каталогом», дающим качественную оценку всех ФЖ для множества значений констант C₀. Это свойство хорошо известно и используется при исследовании фракталов [1, 7], но, на наш взгляд, недостаточно широко применяется при создании фрактальных изображений. В настоящей работе было рассмотрено множество различных функций F(z) (многие из связанных с ними фракталов часто встречаются в интернете под собственными названиями, например, - «паук», «горящий корабль»), в том числе ряд найденных авторами (например, на рис. 2, б); для каждой из них строилось изображение типа ФМ, а также совокупность миниатюр типа ФЖ для различных значений константы C₀, взятой с некоторым шагом). На рис. 3, а показаны примеры «каталогов» таких миниатюр (слева - фрактал «паук» и набор миниатюр, справа - миниатюры к фракталу «горящий корабль»). Наборы миниатюр позволяют бегло оценить образы, порождаемые данным видом функции и выбрать какой-либо из вариантов для более детального анализа в ходе поиска подходящих изображений.
Кроме двух перечисленных фрактальных множеств, лежащих в основе соответствующих алгоритмов, был рассмотрен также фрактал Ньютона (ФН), который представляет собой фрактал Жулиа для особого вида функции: F(z)=z-f(z)/f'(z), - итерационной формулы поиска корней уравнения методом Ньютона [1, 7]. Построение фрактала типа ФМ для таких функций авторам настоящей работы прежде не встречалось и впервые было предложено в [8]. Подход с совместным использованием алгоритмов ФМ и ФЖ был применен и к фракталам типа Ньютона. В то время как фракталы Ньютона для различных значений константы C весьма сходны между собой, обобщающий их ФМ оказывается довольно любопытным. На рис. 3, б показано изображение типа ФМ для множества фракталов Ньютона поиска корней функции f(z)=z³-C и набор миниатюр, на рис. 3, в - изображение типа ФМ для фракталов поиска корней функции f(z)=z²+pz+q, где значения действительных коэффициентов p/q задавались как действительная и мнимая части C (фрактал и миниатюры ранее были показаны в [8]).

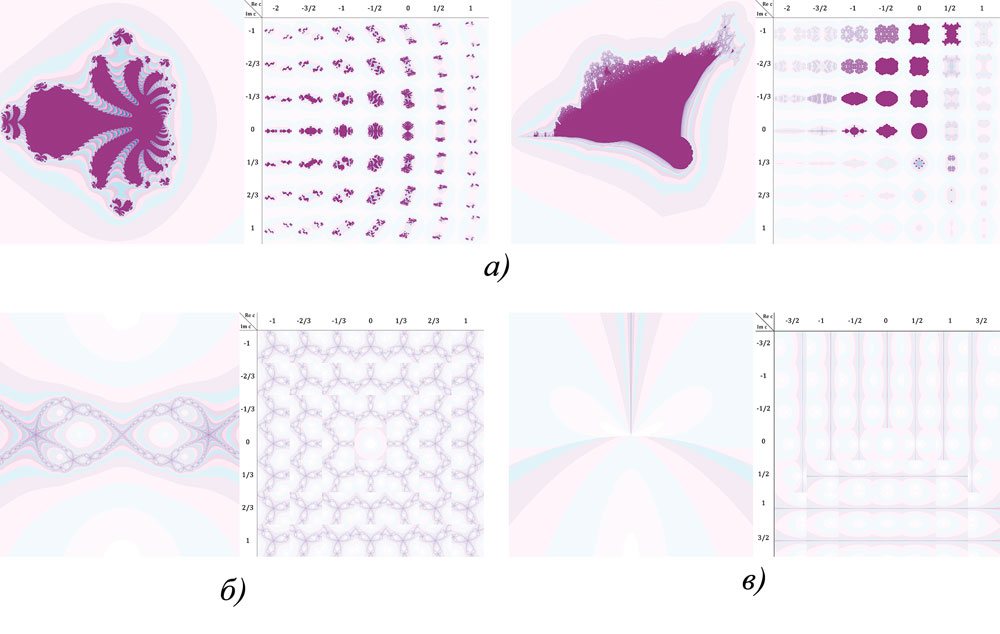
Рис. 3. Фракталы Мандельброта и наборы миниатюр фракталов Жулиа:
а - «паук» и «горящий корабль», б - на основе итерационной формулы Ньютона
для поиска корней функции f(z)=z³-C, в - функции f(z)=z²+pz+q

Рассмотренные фракталы позволили сделать вывод о целесообразности совместного использования ФМ и ФЖ, в том числе для фракталов типа Ньютона, для поиска подходящих визуальных образов. В качестве функций - источников фрактальных изображений могут использоваться функции комплексного переменного любого вида (для ФЖ и ФН) либо функции комплексного переменного вида F(z, C) и F(Z, p, q), где C - комплексное число, p и q - действительные числа (для ФМ, где каждая пара p/q или значение С используется для запуска связанного алгоритма ФЖ). Выбирая функцию F(z), содержащую только одну константу C (F(z, C) или F(z, p+iq)), мы получаем ∞² различных фрактальных изображений (ФЖ), каждое из которых можно увеличивать, выбирая наиболее удачные фрагменты. Подставляя функцию F в формулу Ньютона в качестве f(z), можно получить еще ∞² новых изображений (итерационная формула - F*(z, C)=z - F(z, C)/F'(z, C) ). При большем числе дополнительных параметров функции F (три и более действительных или два и более комплексных), дискретная модель ФМ требует трех- и более мерной матрицы, то есть фрактальный образ оказывается более чем двухмерным, что непосредственно подводит нас к многомерному обобщению алгоритмов типа ФМ и ФЖ.

Алгебраические фрактальные алгоритмы с позиций многомерной геометрии. Гиперфракталы

Несмотря на качественные различия фрактальных множеств Жулиа и Мандельброта, вычислительные алгоритмы построения дискретных моделей соответствующих фракталов очень похожи. Приведем их:

// общий вид функции итерации для алгоритма построения фрактала Мандельброта
maxIterationsCount = 40; // максимальное число итераций
R_max = 2; // максимальное значение модуля числа Z

функция функция_итерации (x, y): цвет;
начало
    Z = комплексное_число (0, 0);
    C = комплексное_число (x, y);
    Для k:= 0 до maxIterationsCount-1
        Если |Z|>R_max² прервать
        Z = F(Z, C)
    Конец для
    вернуть цвет_для_итерации(k);
конец;

// общий вид функции итерации для алгоритма построения фрактала Жулиа
maxIterationsCount = 40; // максимальное число итераций
R_max = 2; // максимальное значение модуля числа Z
C₀ = комплексное_число (re₀, im₀); // константа функции итерации

функция функция_итерации (x, y): цвет;
начало
    Z = комплексное_число (x, y);
    Для k:= 0 до maxIterationsCount-1
        Если |Z|>R_max² прервать
        Z = F(Z, C₀)
    Конец для
    вернуть цвет_для_итерации(k);
конец;

В обоих случаях F(Z, C) = z²+C.

Различие алгоритмов состоит в интерпретации параметров x, y (координат ячейки матрицы фрактала) - в первом случае они используются для формирования константы C₀, во втором - начального значения z₀. Таким образом значение цвета ячейки матрицы, фактически, при использовании одной и той же функции F определяется значениями двух комплексных параметров - C₀, z₀. Считая компоненты комплексных значений независимыми действительными переменными, функцию определения цвета ячейки можно представить в виде - ЦВЕТ = Iterate (C₀^re, C₀^im, z₀^re, z₀^im), эта функция определяет некоторую гиперповерхность Г пятимерного пространства с координатами (ЦВЕТ, C₀^re, C₀^im, z₀^re, z₀^im), состоящую из ∞⁴ точек. Будем называть ее гиперфракталом размерности ∞⁴. Применительно к такому пятимерному пространству уравнение Ф(ЦВЕТ, C₀^re, C₀^im, z₀^re, z₀^im)=0 выделяет некоторое 4-мерное подпространство, пара уравнений:

Ф₁(ЦВЕТ, C₀^re, C₀^im, z₀^re, z₀^im)=0
Ф₂(ЦВЕТ, C₀^re, C₀^im, z₀^re, z₀^im)=0
- некоторое трехмерное подпространство, линейное или кривое, а тройка уравнений - поверхность из ∞² точек. ФМ получается заданием соответствующего значения  z₀, что равносильно системе уравнений:

ЦВЕТ = Iterate (C₀^re, C₀^im, z₀^re, z₀^im),
z₀^re=A,
z₀^im=B,
а любой из семейства ФЖ получается заданием начального значения C₀, что равносильно системе уравнений:

ЦВЕТ = Iterate (C₀^re, C₀^im, z₀^re, z₀^im),
C₀^re=A,
C₀^im=B,
- и в том, и в другом случае полученный фрактал представляет собой проекцию некоторой поверхности, которая является сечением гиперфрактала Г. Эта проекция сходна с проекцией с числовыми отметками, где роль числовой отметки выполняет цвет. Добавление еще одного уравнения, например, ЦВЕТ = const выделяет уже некоторые кривые типа эквипотенциальных (см. [9]), построение узора таких кривых может представлять самостоятельную дизайнерскую задачу.

Отметим, что функция Iterate, задающая гиперфрактал Г, является однозначной, так что каждой четверке значений C₀^re, C₀^im, z₀^re, z₀^im соответствует ровно одно значение цвета. Это обстоятельство существенно, поскольку при визуализации позволяет работать с четырехмерным пространством (C₀^re, C₀^im, z₀^re, z₀^im), заполняющим гиперповерхность Г изнутри и целиком состоящим из разноцветных точек, его дискретную модель можно представить четырехмерной матрицей элементов, содержащих информацию о цвете отдельных ячеек-вокселов. В таком пространстве уравнение Ф(C₀^re, C₀^im, z₀^re, z₀^im)=0 выделяет трехмерное пространство цветных точек, а пара уравнений - поверхность из ∞² цветных точек. ФМ и ФЖ, опять-таки, задают плоские сечения гиперфрактала как плоскости цветных точек, своеобразные «томограммы» гиперфрактала Г. С этой точки зрения указание на ФМ некоторой точки равнозначно выбору особой проецирующей плоскости ([10, 11]), в которой лежит соответствующий ФЖ. Точно так же выбор некоторой точки на любом ФЖ равнозначен выбору плоскости, в которой лежит другое плоское сечение гиперфрактала типа ФМ, полученное для z₀=const (в общем случае, z<>0). Вообще при математическом исследовании множеств Мандельброта и Жулиа выбор начального значения z₀ строго определен и связан с обращением в 0 производной исследуемой функции F, однако в случае гиперфрактала такое ограничение соответствует выбору на гиперповерхности Г некоторой особой двухмерной поверхности (типа особой линии - окружности 0-го радиуса в вершине конической поверхности), в то время как остается еще множество неособых поверхностей. Каждая из них может представлять интерес в дизайне. На рис. 4 показан набор миниатюр, представляющих собой ФМ для различных начальных значений z₀.

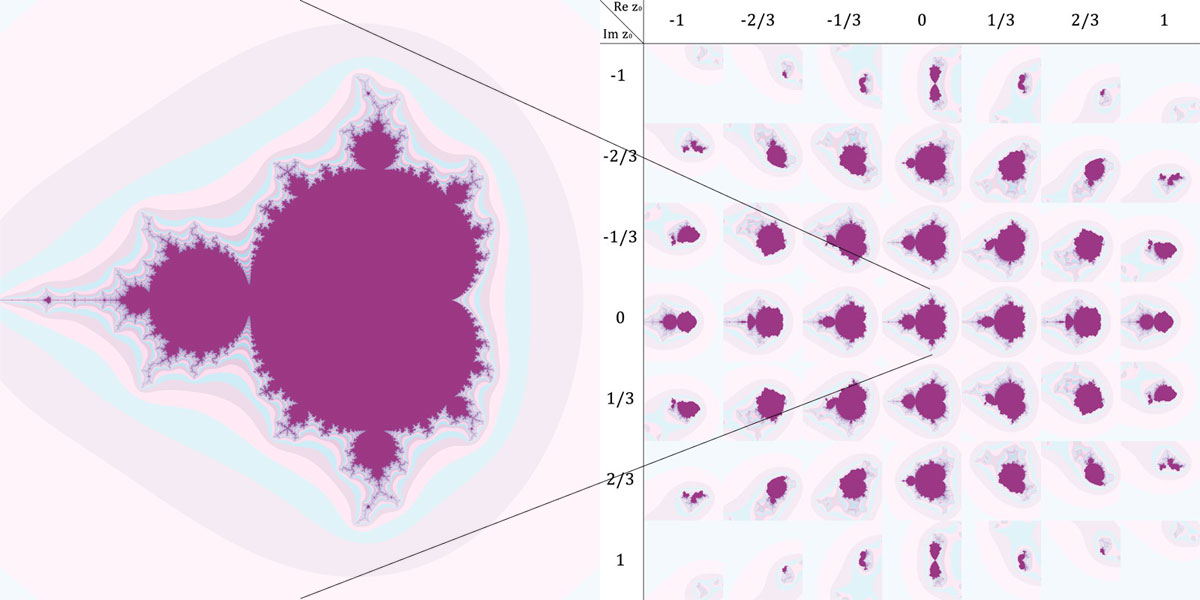
Рис. 4. Фрактал Мандельброта для z₀=0 и набор миниатюр для других значений z₀

Из сказанного непосредственно вытекает способ создания новых фрактальных изображений как сечений гиперфрактала F плоскостями общего положения или кривыми поверхностями (сферами, цилиндрами). Для этого достаточно задать зависимость C₀ от z₀ (или наоборот) в виде уравнений:

C₀^re = s₁(z₀^re, z₀^re),
C₀^im = s₂(z₀^re, z₀^re),

Рассмотрим построение сечений гиперфрактала связкой плоскостей, которую зададим следующим образом:

t·(C₀ - A)+u·(z₀ - B) = 0 (A, B, C₀, z₀ - комплексные числа, u и t - действительные)

Очевидно, при t=0 секущая плоскость оказывается плоскостью фрактала типа Мандельброта (z₀=B), при u=0 - плоскостью одного из фракталов Жулиа (C₀=A). Если принять u=1 - t, то связка превращается в пучок плоскостей, который позволяет получить последовательное превращение любого из вариантов ФЖ в ФМ:

t·(C₀ - A)+(1 - t)·(z₀ - B) = 0

На рис. 5, а показан набор миниатюр для сечений плоскостями пучка, которые получаются при изменении t от 0 до 1. 

Рис. 5. Сечения гиперфракталов пучками плоскостей:
а - сечения гиперфрактала размерности ∞⁴ (превращение ФЖ в ФМ), 
б - сечения гиперфрактала размерности ∞⁶ (превращение фрактала «паук» в ФМ)

Рассмотренный подход можно использовать и для дальнейших обобщений известных фрактальных формул. В частности, итерационные формулы ФМ и фрактала «паук» различаются тем, что значение константы C при построении ФМ не изменяется, а при построении фрактала «паук» меняет значение от итерации к итерации по формуле C_i+1=0,5·C_i+Z_i+1.  

Для ФМ: Z_i+1 = Z_i²+C_i. C_i+1 = C_i. Для фрактала «паук»: Z_i+1 = Z_i²+C_i. C_i+1 = C_i/2+Z_i+1.

Если сравнить итерационные формулы, легко заметить, что вторую из первой можно получить, введя две дополнительные действительные переменные - t и m таким образом, чтобы создать зависимость константы C от предыдущего значения, а также текущего положения точки z: C_i+1=t·C_i+m·Z_i+1. Это позволяет задать итерационную функцию ЦВЕТ = Iterate (t, m, C₀^re, C₀^im, z₀^re, z₀^im), которая выделяет 6-мерную гиперповерхность Г в 7-мерном пространстве (ЦВЕТ, t, m, C₀^re, C₀^im, z₀^re, z₀^im) или гиперфрактал размерности ∞⁶. При t=1, m=0, фрактал превращается в гиперфрактал размерности ∞⁴ классического ФМ, при t=0.5, m=1 - в гиперфрактал «паука». Классические ФМ и «паук» являются его сечениями. Как и в предыдущем случае, несложно сконструировать связки или пучки плоскостей, которые позволяют превратить «паука» в ФМ. На рис. 5, б приведен набор миниатюр сечений таким пучком (значения t, m определяются номером шага перехода).

Таким образом, рассматривая алгебраические фракталы с позиций многомерной геометрии, можно получить множество новых фрактальных образов как сечений подходящего гиперфрактала плоскостями или кривыми поверхностями. Этот подход может применяться, в частности, для создания переходных вариантов фрактальных изображений, когда исходные изображения получены на основе единой итерационной формулы.

Создание фрактальных образов методом сложения итерационных формул

Выше было показано, что переходные фрактальные образы могут быть получены, если исходные изображения создаются на основе единой итерационной формулы, задающей гиперфрактал, как плоские или неплоские сечения гиперфрактала. Однако итерационные формулы различных фракталов, как правило, сильно различаются. Для формирования переходных образов двух произвольных исходных итерационных формул можно использовать метод сложения функций, широко применяющийся в прикладной геометрии для конструирования кривых и поверхностей [10, 11]. Пусть первый фрактал получается на основе итерационной формулы F₁(x,y), а второй - на основе формулы F₂(x,y), тогда плавный переход между исходными образами можно выполнить при помощи следующей формулы:

t·F₁(x,y) + (1 - t)·F₁(x,y) = 0

При t=1 будет получен первый образ, при t=0 - второй, при 0<=t<=1 различные переходные варианты, а при t<0 или t>1 - неизвестные. Сложение функций можно представить и в более общем виде:

u·F₁(x,y) + v·F₁(x,y) = 0,

Сложение функций можно использовать и в варианте сложения гиперфракталов:

ЦВЕТ = u·Iterate₁ (C₀^re, C₀^im, z₀^re, z₀^im) + v·Iterate₁ (C₀^re, C₀^im, z₀^re, z₀^im)

На рис. 6 показаны примеры таких переходов. Дальнейшие исследования в указанной области позволят строить фрактальные изображения, соединяющие по замыслу дизайнера требуемые элементы различных фракталов в рамках единого изображения.

Рис. 6. Варианты фракталов, полученные способом сложения итерационных формул (гиперфракталов)

Практическое применение фракталов

Выше были показаны способы создания различных новых фрактальных изображений на основе известных. Рассмотрим возможности их применения на практике. С точки зрения дизайна интерес представляют (рис. 7, а):
a – фрактальные фоны, составляющие большую часть фрактального изображения, – получаются естественным образом в ходе его построения;
b – «кружки», образованные точками, в которых итерационный процесс сразу же прекращается, – их удобно использовать для размещения торговых марок, логотипов, эмблем и т.п.;
c – фрактальные границы, возникающие вокруг областей притяжения, являясь естественной частью фрактального узора, – могут служить разделителями между текстовыми и графическими блоками, при этом фрактальные границы имеют неоднородную структуру и визуально более насыщенны, чем обычные разделительные линии;
d – фрактальные острова – могут служить зонами для размещения заголовков и небольших текстовых фрагментов внутри области фрактального фона.

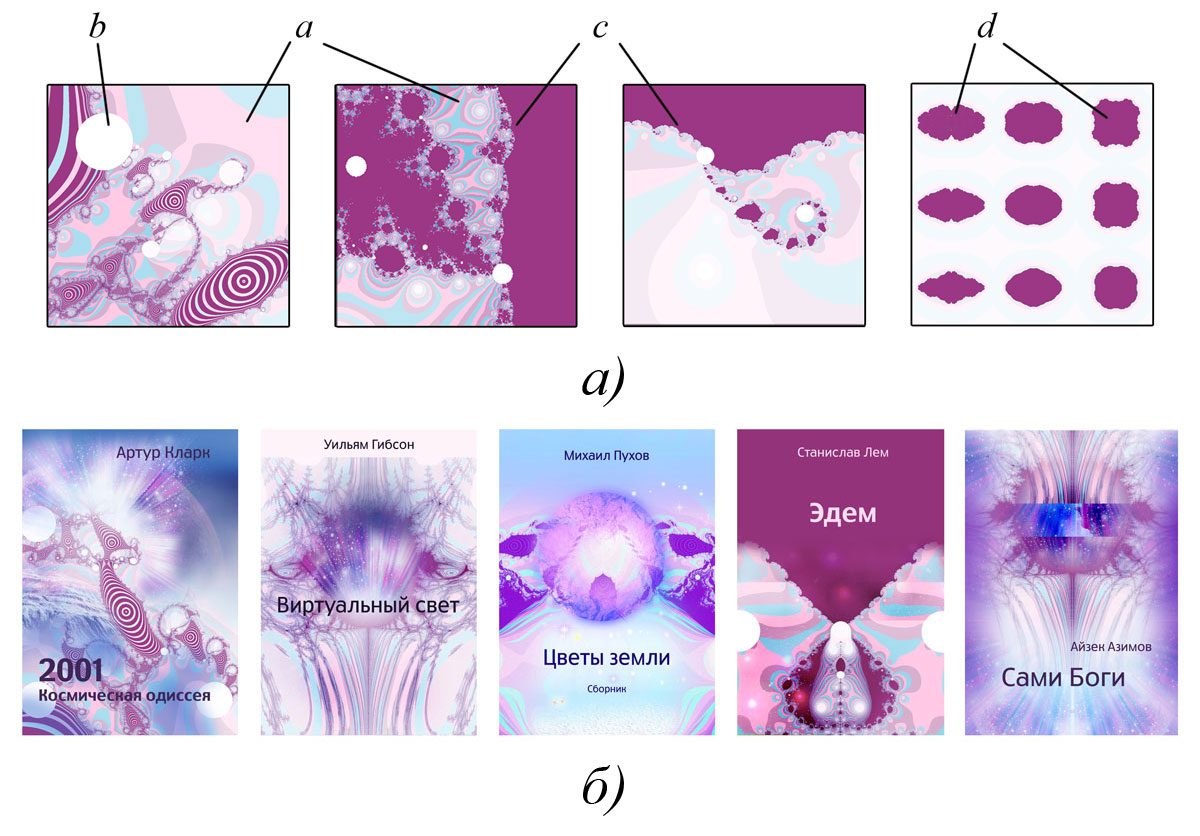
Рис. 7. Элементы фрактальных узоров и проекты книжных обложек с использованием полученных фракталов

На рис. 7, б показаны проекты книжных обложек, при создании которых были использованы рассмотренные в настоящей работе способы получения новых фракталов. Фрактальные изображения подходят для создания рамок, паспарту, фонов, логотипов, монохромные – также для рельефных текстур. 

Программное обеспечение для создания фрактальных образов

Для построения алгебраических фракталов, в том числе наборов миниатюр (сечений гиперфракталов и переходных серий), были созданы программы на языке c#. Достоинствами этого языка являются простота создания прикладных программ, наличие встроенных графических средств, а также возможность выполнять вычисления с комплексными числами, как с обыкновенными. Все изменения (новая итерационная формула, новые значения констант и параметров и др.) вносились непосредственно в код программ. Этот подход дает свободу для экспериментов, но требует владения навыками программирования, установки инструментальной среды Visual Studio и др. 
Для решения практических задач дизайнерами-непрограммистами требуется создание специального редактора. Были сформулированы требования к такому редактору и спроектирован его интерфейс. Функции редактора включают следующее:
•    выбор итерационной формулы из предопределенного списка, в частности, один из пунктов этого списка (формула пользователя) должен давать возможность расширять набор встроенных фракталов;
•    выбор и настройка цветовой схемы фрактального изображения;
•    настройка экспорта фрактального изображения (размер кадра, тип файла и т. п.);
•    автоматическое формирование нескольких изображений (в том числе целых серий) в высоком разрешении в «пакетном режиме»;
•    навигация по гиперфракталу (рис. 8), для чего в интерфейсе предусмотрены следующие элементы – образ ФМ для данной формулы и набор соответствующих миниатюр ФЖ, область предпросмотра выбранного варианта ФЖ и набор миниатюр ФМ; наборы миниатюр используются для загрузки соответствующих вариантов фрактала в области предпросмотра, указание точки в такой области также позволяет сгенерировать соответствующий ФМ или ФЖ; навигация также предполагает возможность явного указания участка фрактала для отображения и изменения масштаба;
•    миниатюры из наборов и образы из областей предпросмотра можно сохранять в собственном (пользовательском) наборе, группировать в папки и использовать в дальнейшем;
•    инструменты «сечения гиперфрактала» и «сложение гиперфракталов»; сгенерированные новые фракталы при помощи этих инструментов также могут быть сохранены в пользовательском наборе.

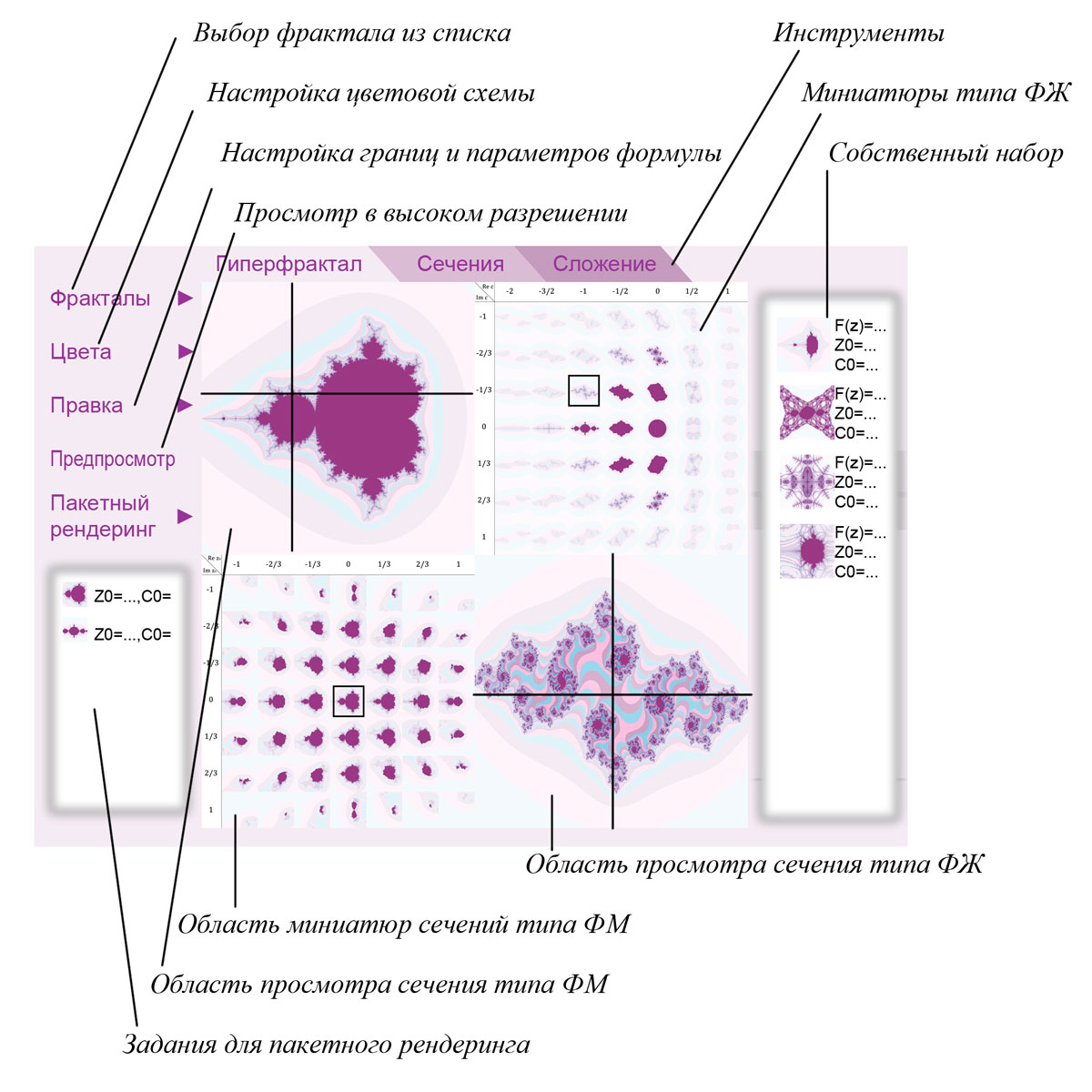
Рис. 8. Проект интерфейса редактора фракталов

Основные результаты

В ходе работы были рассмотрены алгебраические фрактальные алгоритмы построения множеств Мандельброта и Жулиа, в том числе варианты для различных итерационных формул, а также фракталы Ньютона. Для всех фракталов типа ФМ было рассмотрено построение также наборов миниатюр типа ФЖ. Предложено строить фракталы типа ФМ для итерационных формул Ньютона поиска корней. Фрактальные алгоритмы типа ФМ и ФЖ рассмотрены с позиций многомерной геометрии, как частные сечения одного гиперфрактала. Предложено строить новые фрактальные изображения как плоские и неплоские сечения гиперфрактала. Показаны примеры таких сечений. Показана возможность получения переходных вариантов фрактальных изображений между парой сечений. На примере ФМ и фрактала «паук» рассмотрено объединение двух фрактальных алгоритмов в рамках общего гиперфрактала более высокого порядка и возможность получения переходных фрактальных алгоритмов между двумя исходными, как сечениями такого гиперфрактала. Для построения переходных вариантов изображений для любой пары исходных фрактальных изображений предложено использовать сложение итерационных формул или гиперфракталов, показаны примеры таких переходов. Полученные фрактальные изображения использованы для создания обложек книг. Описан набор функций специального фрактального редактора, реализующего описанные в статье возможности, спроектирован его интерфейс. Планируется создание редактора для использования при решении задач дизайна и полиграфии. Представляет интерес дальнейшее исследование одномерных серий переходных фракталов, которые, если рассматривать их как плоские сечения некоторого предмета, можно использовать для формирования его трехмерной модели «по слоям» и последующей печати на 3D-принтере. Такие пространственные фрактальные формы могут найти применение в предметном дизайне или дизайне интерьеров.

Список литературы

1. Пайтген Х., Рихтер П. Красота фракталов. Образы комплексных динамических систем. М.: Мир, 1993. 176 с.
2. Бердичевский Е.Г. Фрактальные технологии в дизайне и технической эстетике // Гуманитарные технологии в современном мире Материалы V Всероссийской научно-практической конференции с международным участием. – 2017. – С. 146-149.
3. Бердичевский Е.Г. Эстетика фракталов в искусстве и дизайне // Труды Академии технической эстетики и дизайна. – 2016. – № 2. – С. 18-21.
4. Трубочкина Н.К. Новый промышленный дизайн и технологии, как результат математическо-компьютерных фрактальных исследований // Качество. Инновации. Образование. – 2012. – Т. 84. № 5. – С. 76-82. 
5. Николаева Е.В. Исследование фракталов в изобразительном искусстве [Электронный ресурс] // Художественная культура. – М. : Государственный институт искусствознания, 2012. – № 3 (4). URL: http://artculturestudies.sias.ru/2012-3/istoriya-i-sovremennost/512.html
6.  Шлык В.А. Фракталы в абстрактном искусстве и дизайне // Известия Челябинского научного центра. – Вып. 1 (22), 2004. – С. 231–244.
7. Морозов А.Д. Введение в теорию фракталов. М.-Ижевск, 2002. 160 с.
8. Шкилевич А.А. Графическое исследование функций комплексного переменного // Тринадцатая международная научно-техническая конференция студентов, аспирантов и молодых ученых «Энергия-2018»: Материалы конференции. Т. 5. – Иваново: ФГБОУ ВО «Ивановский государственный энергетический университет им. В.И. Ленина», 2018. – С. 135.
9. Милнор Дж. Голоморфная динамика. – Ижевск, 2000. – 320 с.
10. Филиппов П.В. Начертательная геометрия многомерного пространства и ее приложения. – Л.: Изд-во Ленингр. ун-та, 1979. – 280 с.
11. Бойков А.А. О построении моделей объектов пространства четырех и более измерений в учебном процессе // Геометрия и графика. – 2018. – Т. 6, № 4. – С. 54–71. – DOI: 10.12737/article_5c21f96dce5de8.36096061 (Краткий вариант в виде доклада на КГП-2017 http://dgng.pstu.ru/conf2017/papers/57/)
12. Обухова В. С. Применение метода сложения выпуклых кривых к конструированию каналовых поверхностей / В. С. Обухова, О. В. Василевский // Прикладная геометрия и инженерная графика. – Киев: Будівельник, 1978. – Вып. 26. – С. 15–17.
13. Воробкевич Р. И. Конструирование поверхностей способом сложения функций, описывающих заданные сечения / Р. И. Воробкевич // Прикладная геометрия и инженерная графика. – Киев: Будівельник, 1986. – Вып. 42. – С. 40–42.

Хейфец Александр Львович (24 марта 2019 г. 12:24)	Коллеги, работа впечаляет  красотой приведенных фракталов. Научную глубину оценить не берусь. Интересуюсь программной реализацией. Сколько по времени занимает построение одного характерного фрактала. Какие требования к ресурсу компьютера.  Есть некоторый опыт построения фракталов в рамках обучения студентов AutoLisp'у. Попроще, не таких эффектных. Насколько мне известно, Алексей Александрович с этим языком знаком.  Как Вы считаете, реально ли построение таких красот на этом  языке. С уважением. А.Л. Хейфец.
Сальков Николай Андреевич (24 марта 2019 г. 12:56)	Добрый день, Алексей Александрович, Екатерина Витальевна и Анастасия Владимировна! Наконец- то, Алексей Александрович, вышла в свет Ваша работа! Александр Владиславович Селиверстов, оценивший Ваши работы с точки зрения красоты, будет доволен - теперь действительно есть применение фракталам в области дизайна. Вспоминается, что Виктор Николаевич Гамаюнов, придумавший такое ответвление как названная им проективография, защитил докторскую по искусствоведению.на базе компьютерных технологий по специальности Техническая эстетика и дизайн. Я с ним часто беседовал на разные темы, он тоже был определенным противником НГ, только мы, кто с ним работал в то время в МГАКХиС, не могли понять, как в его теории можно получить изображения кривых поверхностей. С уважением, Н.А. Сальков
Селиверстов Александр Владиславович (24 марта 2019 г. 15:36)	Здравствуйте, Алексей Александрович, Екатерина Витальевна, Анастасия Владимировна и Шкилевич А.А. (увы, имя соавтора не указано). Доклад хороший. Заодно иллюстрирует пользу от использования комплексных чисел при работе с обычными изображениями на плоскости. Но неужели в подписи к рис. 2 многоточие (F(z) = ...) оставлено для секретности? С уважением, А.В. Селиверстов
Карабчевский Виталий Владиславович (24 марта 2019 г. 16:38)	Здравствуйте, Алексей Александрович! Прочитал с большим интересом. На моей кафедре читают для дизайнеров курс "Фракталы и сжатие изображений", покажу Вашу статью лектору. С уважением, В.В. Карабчевский.
Мухаркина Анна Анатольевна (25 марта 2019 г. 1:15)	Коллеги, фракталы прекрасны, а обложки ждут рук мастера, уж извините. Это Вам в коллекцию использования фракталов в дизайне - фракталы Фаберже https://mymodernmet.com/tom-beddard-subblue-faberge-fractals/ https://www.etsy.com/listing/209120745/modern-light-bedroom-light-fractal?ref=shop_home_active_12&ep_click=1&crt=1 С уважением, Анна Мухаркина
Бойков Алексей Александрович (26 марта 2019 г. 14:17)	Здравствуйте, Александр Львович! Спасибо за высокую оценку доклада. Прошу прощения за поздний ответ, два дня в дороге. Попробую ответить на вопросы. Время на построение определяется размерами картинки в пикселах (WxH) и числом итераций (K) для каждого пиксела, то есть при наихудшем исходе пропорционально ~WxHxK. Мой собственный опыт подобных программ на Delphi показывает для картинки 800x800x40 на персональном компьютере семилетнего возраста порядка 1,5-2 мин, хотя я видел примеры построения фрактала Мандельброта практически в реальном времени. Екатерина и Анастасия делали изображения в высоком разрешении - около 4тыс.пикселов на сторону и с большим числом итераций. Время формирования до 40 минут, поэтому в проекте приложения заложен пакетный режим формирования, когда запустил - и пошел спать. Насчет создания картинки в AutoLISPе у меня встречный вопрос - позволяет ли он вообще создавать растровые картинки по пикселам? Другой тип фракталов - геометрические для чертежной программы вполне "по зубам", поскольку можно рекурсивно добавлять в модель отрезки, кружки и пр., но алгебраические фракталы, как правило, строятся по пикселам. Существуют алгоритмы, в той же книге [1], по-моему, для построения контуров множества Мандельброта или эквипотенциальных кривых. Такую картинку в AutoCADе построить можно вполне. В любом случае производительность будет низкая, поскольку AutoLISP работает в режиме интерпретатора. с уважением, А.Бойков
Бойков Алексей Александрович (26 марта 2019 г. 14:34)	Здравствуйте, Николай Андреевич! Спасибо за теплые слова. С проективографией почти не знаком, слышал краем уха, хотя книга (почти журнал с иллюстрациями!) Гамаюнова В.Н. в личной базе в фотокопии имеется. Почитаю. с уважением, А.Бойков
Бойков Алексей Александрович (26 марта 2019 г. 15:21)	Здравствуйте, Александр Владиславович! Спасибо за высокую оценку и справедливые замечания. Четвертого автора зовут Шкилевич Антон Александрович, он в 2017 году начал эту работу по систематическому построению миниатюр фракталов типа ФЖ для различных функций и фракталов типа ФМ, но в этом году в период проведения конференции не смог присоединиться к нам. Значки "...", конечно, конспирация. Мы несколько раз перерабатывали текст, вначале планировалось все формулы вписать текстом, потом решили встроить формулы в картинки, в итоге - накладка. Прошу прощения. Подрисуночная подпись должна быть: Рис. 2. Примеры фракталов: а - один из фракталов Жулиа (C0 = -0.8-0.2i) в двух цветовых вариантах;  б - фракталы, найденные авторами (z
Бойков Алексей Александрович (26 марта 2019 г. 15:28)	Вставляю картинкой. Подрисуночная подпись должна быть: с уважением, А. Бойков
Бойков Алексей Александрович (26 марта 2019 г. 15:49)	Здравствуйте, Виталий Владиславович! Большое спасибо за внимание к статье и высокую оценку. В ИГЭУ фрактальные алгоритмы бегло рассматриваются на факультете информатики и вычислительной техники в рамках третьей части дисциплины "Инженерная и компьютерная графика" (ранее курс назывался "Алгоритмы машинной графики"), зато появляется возможность познакомиться подробнее в рамках творческих работ. с уважением, А.Бойков
Бойков Алексей Александрович (26 марта 2019 г. 16:08)	Здравствуйте, Анна Анатольевна! Спасибо за внимание к статье и замечания. Главная проблема созданных в рамках исследования программ - невозможность выбирать и корректировать цветовую гамму. Эта проблема будет решена в создаваемом редакторе. Приведенные Вами ссылки ведут на примеры геометрических, не алгебраических фракталов, хотя, несомненно, красивых. с уважением, А.Бойков