ВЛИЯНИЕ ДАТЫ РАСЧЕТА НА ПРОДОЛЖИТЕЛЬНОСТЬ ИНСОЛЯЦИИ (как задача геометрического моделирования)
English version

|
Хейфец Александр Львович | (Южно-уральский государственный университет (Национальный Исследовательский Университет)) |
Аннотация
Актуальность исследования обусловлена изменением нормативной даты расчета инсоляции с 22 марта на 22 апреля. Показано, что при расчете на 22 апреля наряду с ожидаемым увеличением плотности застройки, имеет место снижение инсоляции в зданиях угловой формы. Приведено исследование этого эффекта и примеры, показывающие его проявление. Исследование выполнено компьютерным 3d моделированием в пакете AutoCAD с применением специализированной программы.
Ключевые слова: инсоляция, нормативная дата, алгоритм инсоляции, 3d моделирование.
1. Введение
Инсоляция – освещение объектов прямым солнечным светом. При проектировании зданий расчет продолжительности инсоляции является обязательным. Расчет выполняется в соответствии с действующими нормами [1,2], среди которых задана дата расчета.
До 2017 г. для центральной зоны России расчет выполнялся на 22 марта или 22 сентября – это день равноденствия. В 2017 г. установлена новая дата расчета – 22 апреля или 22 августа. При новой дате возрастает высота солнца над горизонтом и продолжительность дневного времени суток. Это позволяет повысить плотность застройки [3,4,5].
Цель нашей работы – исследование геометрических особенностей инсоляции в связи с изменением нормативной даты расчета.
2. Алгоритм расчета
Исследования выполнялись в пакете AutoCAD [6,7] применением программы расчета инсоляции [8,9], путем построения и исследования полей инсоляции [3,4,10] .
Для определения продолжительности инсоляции в точке А (рис. 1, а) строим 3d модели зданий в произвольном масштабе. Строим лучевой конус [11], вершину которого помещаем в т. А. Ось конуса i расположена в меридиональной плоскости и наклонена к северу (стрелка N). Угол j равен географической широте. Для Москвы и Челябинска j = 55⁰. Угол δ определяется по формуле Купера [12]:
,
где δ – угол в градусах, data – номер календарного дня. Например, для 1 января data =1; для 22 марта data = 81, δ= 0; для 22 апреля data = 112, δ= 11.93⁰, для 22 июня data = 173, δ= 23.5⁰ , для 22 декабря data = 354, δ= –23.5⁰. Конус cone1 соответствует периоду между 22 марта и 22 сентября; cone2 – периоду от 22 сентября до 22 марта. В дни 22 марта и 22 сентября δ =0 и конус преобразуется в плоскость γ (плоскость равноденствия).
Конус срезан на уровне плоскости горизонта horizon É A, при этом определяются луч восхода AB и луч AC заката солнца.
Строим сечения зданий конусом (рис. 1, б). Сечения проецируем на плоскость γ или γ¢ || γ (рис. 1, в). Определяем секторы затенения β1, β2 … и секторы инсоляции α1, α2 … (рис. 1, г). Измеряем углы α и находим их сумму αS. Значение αS преобразуем в интервал времени insol по соотношению 15⁰ = 1 час.
В соответствии с нормами [1,2,3] из αS вычитаем углы ε = 15 градусов (по одному часу) на восходе и закате. Если точка A находится на стене здания, то в этой точке создают 3d модель окна, балкона или лоджии. В упрощенных расчетах вместо этих моделей из αS вычитают предварительно определенные углы h [1,13]. В нашей работе была принята модель гладких стен с h = 8⁰. Алгоритм расчета учитывает еще ряд требований, подробно приведенных в работе [3].
Полученное итоговое значение сравнивается с допустимым значением. Если в точке единственный сектор инсоляции (непрерывная инсоляция), допустимое значение составляет 2 часа, если несколько секторов (прерывистая инсоляция), то 2.5 часа.
Приводимые ниже поля инсоляции образованы расчетом инсоляции внутри контура стены или площадки. Расчеты выполняют в узлах прямоугольной сетки. Количество ячеек сетки по каждому направлению задается в зависимости от требуемой точности в интервале от 50 до 150, то есть от 2500 до 22500 точек на контур. В точках проставляют маркеры, цвет которых определяется значением инсоляции insol (рис. 2, е). Зоны допустимой инсоляции имеют желтый или зеленый цвет. Недопустимая инсоляция выделена красным и синим цветом.
В качестве критерия предельно-допустимого положения или высоты зданий принято появление красной зоны на стенах зданий.
3. Расстояние между зданиями
Рассмотрим изменение полей инсоляции при сближении двух взаимно параллельных зданий, ориентированных вдоль меридиана. Размеры зданий примем одинаковыми: длина 120, ширина 15, высота h= 60.
В марте, при расстоянии del > 105 инсоляция insol всех стен и земли > 3 часов. Исключение составляют северные стены, в которых инсоляция отсутствует. При del = 100 возникает небольшая зона 2<insol<3 зеленого цвета (рис. 2, а). При дальнейшем сближении зданий эта зона возрастает (рис. 2, б). При del=80 на внутренних стенах зданий возникает красная зона в виде тонкой полоски в нижней части стены (рис. 2, в). Это признак появления недопустимо-низкой инсоляции insol < 2 на нижнем этаже зданий. При del=60 красная зона на стене существенно увеличивается (рис. 2, г). При del=55 (рис. 2, д) на стене появилась синяя зона как признак insol < 1 часа, на земле образовалась обширная красная зона. Предельно допустимое расстояние между зданиями, при котором на стенах зданий появляется красная зона, составило del=80 (рис. 2, в).
В апреле картина полей инсоляции качественно повторяется (рис. 2, ж,з,и). Однако допустимое расстояние между зданиями уменьшается. Красная зона возникает при del=55 (рис. 2, з).
Следовательно, по критерию образования красной зоны изменение расчетной даты с 22 марта на 22 апреля позволяет располагать здания на ≈30% ближе.
На той же модели плавно увеличивали высоту обоих зданий до возникновения красной полоски на первом этаже. В марте для del=80 предельная высота составила h=60. В апреле она составила 85. При del=100 для марта предельная высота достигнута при 75. Для апреля – при h=105. То есть, допустимая высота зданий для 22 апреля по сравнению с мартом возросла на ≈30%.
4. Положение здания относительно параллели
22 марта продолжительность светового дня составляет 12 часов. 22 апреля эта продолжительность составляет ≈14 час. 21 мин., то есть увеличилась на ≈2 часа 21 минуту. Для оценки влияния этого фактора единичное здание располагали длинной стороной под углом l к параллели и определяли инсоляцию стены, обращенной на север. Установлено, что в марте предельное значение l= 48⁰. В апреле оно составило 24⁰, то есть снизилось вдвое.
5. Особенности инсоляции здания угловой формы
В предыдущих экспериментах подтверждено ожидаемое увеличение инсоляции в апреле по сравнению с мартом. Однако для зданий угловой формы было установлено, что на внутренних стенах продолжительность инсоляции в апреле по сравнению с мартом снижается. Для выявления причин этого неожиданного эффекта была исследована модель, приведенная на рис. 4, а. В точках 0–20, соответствующих окнам нижнего этажа, измеряли продолжительность инсоляции insol и секторы света α.
Показано (рис. 3, б), что для точек окна 0–11 с переходом от декабря к июню, в том числе от марта к апрелю, инсоляция снижается. Например, в точке 2 (см. рис. 3, б, кривые 4 и 5), при расчете 22 марта продолжительность составила 5 час. 6 мин или 76.5⁰. При расчете 22 апреля продолжительность снизилась до 4 часа 34 минуты или 68.5⁰, то есть на 32 минуты.
Эффект снижения инсоляции проявляется от точки 0 до точки 11.5. В точке 11.5, начиная с февраля по октябрь, инсоляция не зависит от даты расчета. После точки 11.5 восстанавливается обычный эффект возрастания инсоляции по мере приближения к 22 июня. Особенность кривых 1,2 объясняется тем, что в декабре и январе конус света cone2 (см. рис. 1, а) не пересекает высотное здание. По мере удаления точки от угла зданий инсоляция в них асимптотически приближается к инсоляции, определенной при отсутствии высотной части (рис. 3, в).
Приведена модель (рис. 3, г), поясняющая выявленный эффект. Показано изменение угла сектора света, расположенного между стенами углового здания. Углам j и δ приданы значения, повышающие наглядность результата. Видно, что угол α*, измеряемый по лучевому конусу, меньше, чем угол α, измеряемый в марте по плоскости равноденствия. На той же модели можно проследить и другие особенности рассматриваемого эффекта.
Рассмотрим модели двух зданий, как варианты уплотнения застройки (рис. 4, а). Контуры зданий определены для 22 марта как предельно допустимые из условия, что возведенные в заданном месте новые здания не вызывают на окружающих зданиях снижения инсоляции ниже нормы [10,14 ]. Расчет на 22 марта показал (рис. 4, б, г), что на стенах старых зданий нет красных зон. Однако расчет на 22 апреля при тех же уплотняющих зданиях выявил появление красных зон, то есть инсоляция в отдельных участках стен стала ниже нормы. Следовательно, выводы о допустимости застройки, полученные для 22 марта, стали недействительны для 22 апреля.
6. Выводы
Предложена методика оценки геометрической формы и взаимного положения зданий на основе построения полей инсоляции. Допустимые размеры и положение зданий определяются по появлению сигнальных областей красного цвета, соответствующих уровню низкой инсоляции.
Предложенная методика реализуется программой, написанной на языке AutoLisp. Эффективность методики возрастает с уплотнением застройки и увеличением сложности геометрической формы зданий.
В большинстве случаев уплотненной застройки изменение даты расчета с 22 марта на 22 апреля позволяет увеличить высоту зданий и уменьшить расстояние между зданиями на 30%, а также уменьшить предельный угол между северной стеной зданий и параллелью с 48⁰ до 24⁰.
Установлено, что для зданий угловой формы изменение даты расчета с 22 марта на 22 апреля может вызвать снижение инсоляции на внутренних стенах. Это может привести к недостоверности результатов, основанных на расчетах для 22 марта, при переходе на другую дату расчета, в частности, на 22 апреля.
Список литературы
- Санитарные правила и нормы СанПиН 2.2.1/2.1.1.1076-01: Гигиенические требования к инсоляции и солнцезащите помещений жилых и общественных зданий и территорий. – http://best-stroy.ru/gost/r38/311.
- О внесении изменений в санитарные правила и нормы СанПиН 2.2.1/2.1.1.1076-01. http://docs.cntd.ru/document/420398169
- Хейфец А.Л. Продолжительность инсоляции: автоматизация расчета и учебные аспекты. Проблемы координации работы технических вузов в области повышения качества инженерно-графической подготовки студентов: материалы науч.-метод. конф. (с. Дивноморское, 10-16 сентября 2018 г.). Донской гос.техн. ун-т. – Ростов-на-Дону: ДГТУ, 2018. – 227 с. С. 134-148.
- Kheifetc A L (Kheyfets) 2018 Automation of Computation of Insolation Duration in Architectural Design. IOP Conference Series: Materials Science and Engineering (MSE)" vol. 451 №012123 http://iopscience.iop.org/article/10.1088/1757-899X/451/1/012123/pdf
- Росчерком пера нас лишили солнца в квартирах: "Город будет безобразный". http://www.mk.ru/social/2018/03/01/roscherkom-pera-nas-lishili-solnca-v-kvartirakh-gorod-budet-bezobraznyy.html
- Хейфец А.Л. Инженерная 3d-компьютерная графика. Учебник и практикум для академического бакалавриата. / А.Л. Хейфец, А.Н. Логиновский, И.В. Буторина, В.Н. Васильева; под ред. А.Л. Хейфеца. – 3-е изд., пер. и доп. – М.: Изд-во Юрайт, – 2015. – 602 с.
- Хейфец А.Л. Инженерная компьютерная графика. AutoCAD. Опыт преподавания и широта взгляда / А.Л. Хейфец. – М.:Диалог МИФИ. – 2002.– 432 с.
- Хейфец А.Л. Программа автоматического расчета инсоляции / А.Л. Хейфец // Свидетельство о государственной регистрации программы ЭВМ №2010613828. Заявка № 2010612286. Дата поступления 23 апреля 2010 г. Зарегистрировано 10 июня 2010 г.
- Хейфец, А.Л. Система автоматизированного расчета продолжительности инсоляции / А.Л. Хейфец // Вестник Южно-Уральского государственного университета. Серия “Строительство и архитектура”. – Челябинск: Изд-во ЮУрГУ. 2007. – Вып. 4. №14(86), с. 51–54.
- Хейфец А.Л. Расчет продолжительности инсоляции в условиях уплотненной застройки / А.Л. Хейфец // Приволжский научный журнал. – Н. Новгород: ННГАСУ. – 2012. – №3. – С. 9–10, 99–105. – http://www.pnj.nngasu.ru/word/pnj_3(2012).zip
- Архитектурная физика / Под ред. Оболенского. – М: “Архитектура -С”, 2007. – 448 с.
- Формула Купера: https://yandex.ru/images/search?text=формула%20купера%20для%20склонения%20солнца&stype=image&lr=56&source=wiz
- ГОСТ Р 57795-2017 Здания и сооружения. Методы расчета продолжительности инсоляции.
- Хейфец А.Л. Способ определения допустимого объема застройки с учетом продолжительности инсоляции в архитектурном проектировании / А.Л. Хейфец, А.В. Саморуков // Патент на изобретение № 2505853. Заявка № 2012128696. Приоритет изобретения 09 июля 2012. Зарегистрировано 27 января 2014. Срок действия патента до 09 июля 2032 г.
Рисунки к докладу
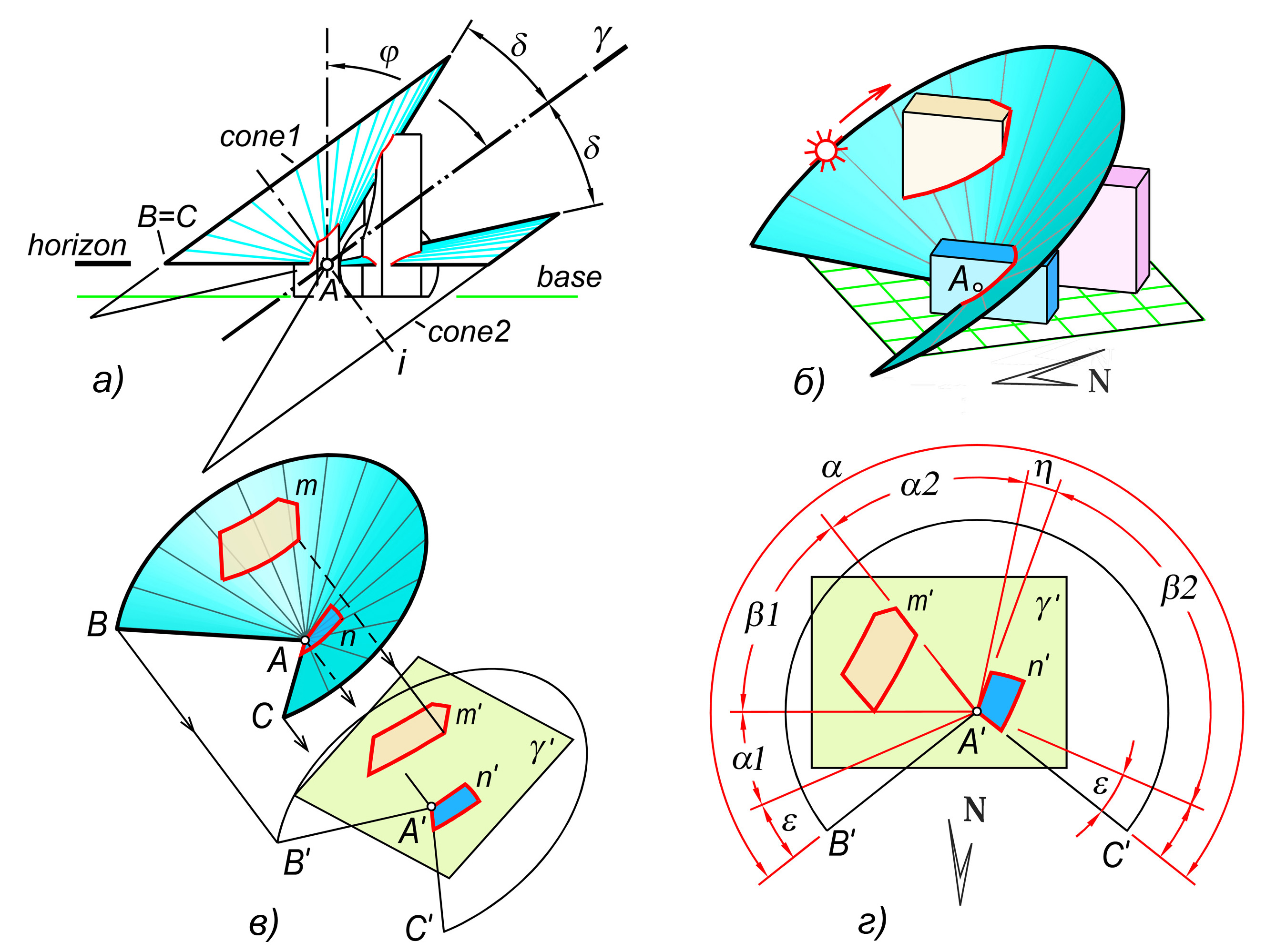
Рис. 1 Алгоритм измерения продолжительности инсоляции: а – параметры лучевого конуса; б – сечения зданий конусом; в, г – измерение углов инсоляции.

Рис. 2 Поля инсоляции в зависимости от расстояния del между зданиями. 22 марта: а – del =100; б – del = 90; в – del = 80; г – del = 60; д – del = 55; е – цвет маркеров. 22 апреля: ж – del = 60; з – del = 55; и – del = 40.
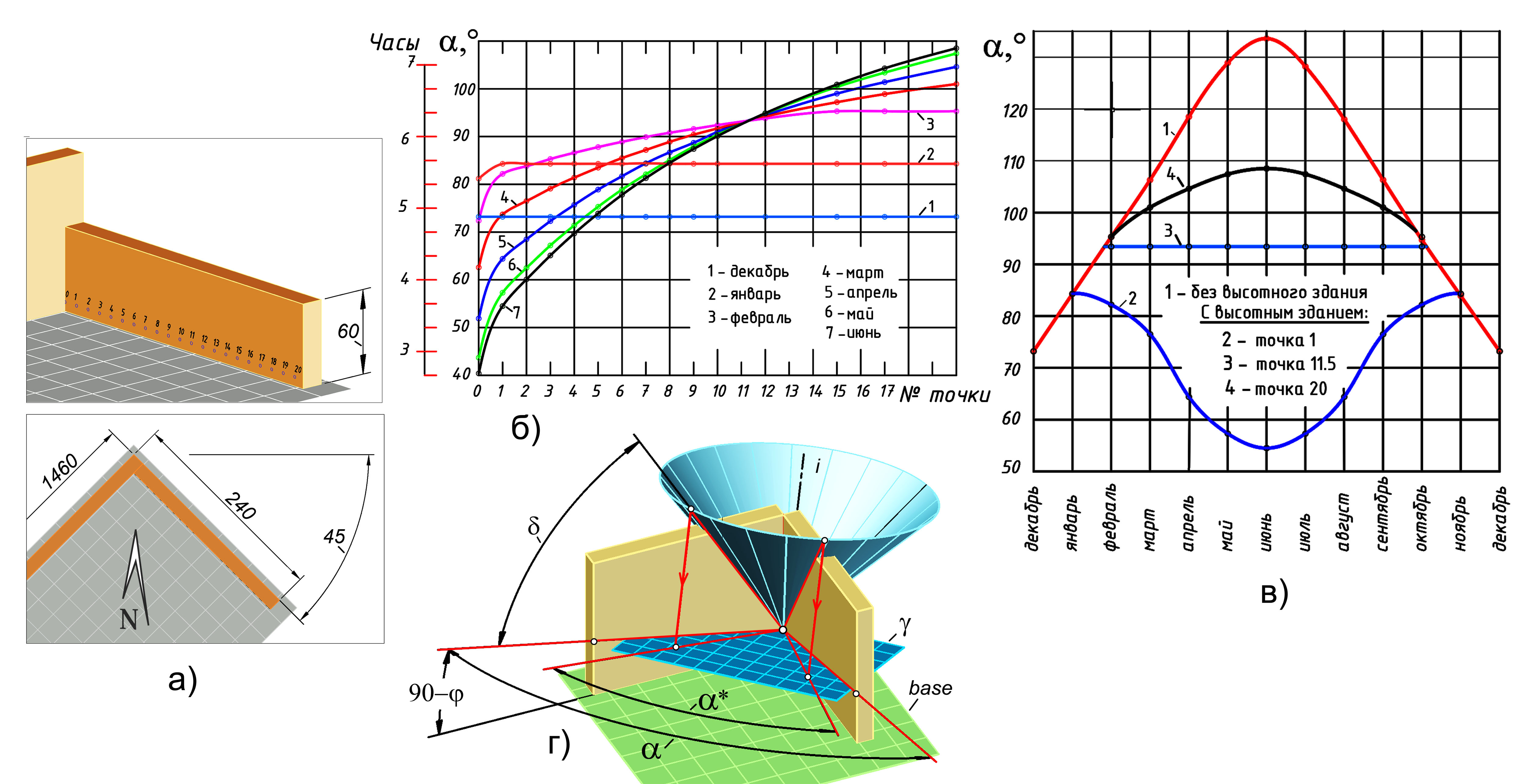
Рис. 3 Особенность инсоляции на стенах углового здания: а – модель здания; б – инсоляция в точках для различного месяца года (дата 22); в – инсоляция в зависимости от месяца; г – модель инсоляции
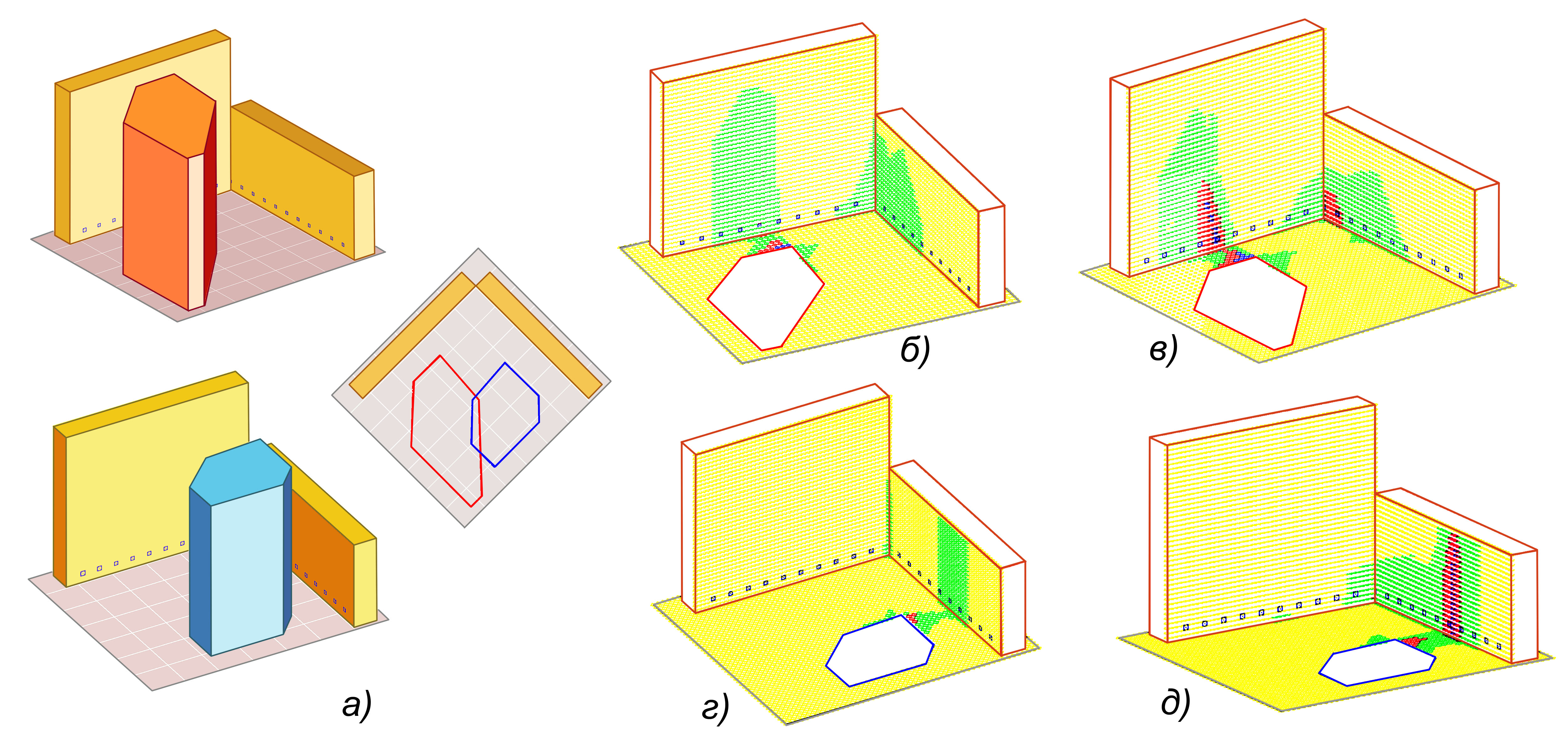
Рис. 4 Инсоляция при уплотненной застройке углового здания: а – модели двух зданий; б, г – инсоляция 22 марта; в, д – 22 апреля
Вопросы и комментарии к выступлению:

Дударь Елена Сергеевна (5 марта 2019 г. 20:07) |
Добрый день, Александр Львович! С удовольствием прочитала Ваш доклад. Расстояние между зданиями нормируются для обеспечения противопожарных требований, для сохранения целостности конструкций, зависят не только от материала стен, но и от материала перекрытий, да, промежутки между окнами тоже должны быть не менее 6 метров. Какие еще нормативные требования учитывались в Ваших расчетах? Используете ли Вы этот исследовательский материал в учебном процессе? С уважением, Елена С. Дударь |

Хейфец Александр Львович (5 марта 2019 г. 20:38) |
Елена Сергеевна, расчет инсоляции лишь один из многочисленных элементов расчета в архитектурном проектировании. Мне эта задача понравилась тем, что она чисто геометрическая: конусы, сферы, линии их пересечения, непростые геометрические построения и измерения. Кроме того, был реальный заказ с последующим многократным внедрением в архитектурных фирмах. Для единичной точки расчета (одного окна здания) все можно сделать вручную. В таком виде я сформулировал КГЗ по курсу НГ. Это задание на построение сечений указанных геометрических объектов. Выдается по вариантам студентам моего курса - строителям. Интерес в том, что это реальная задача, включенная в учебный курс. Для практических приложений требуется расчет тысяч точек, покрывающих стену или территорию. Здесть только программирование. На мой взгляд эта задача - характерный пример современной прикладной задачи геометрического моделирования, где основным инструментом является программирование 3d построений. Пока все. Будет интересно - продолжим беседу на эту тему. И еще. Предполагаю, что кроме Вас никто не откликнется, поскольку здесь собрались методисты и педагоги, а вот реальными задачами мало кто занимается. С уважением. А.Л. Хейфец. |

Дударь Елена Сергеевна (5 марта 2019 г. 22:30) |
Спасибо, Александр Львович, за подробный ответ. Ваш доклад - это именно то, что я ищу на нашей конференции, а именно новые геометрические задачи с практическим приложением. Прекрасно, что Вы изучаете их со студентами. С пожеланием удачи, Елена С. Дударь |

Бойков Алексей Александрович (26 марта 2019 г. 18:41) |
Здравствуйте, Александр Львович! Благодарю за прекрасно иллюстрированный доклад с решением интересной практической задачи. с уважением, А.Бойков |
Назад Go Back