ПРИМЕНЕНИЕ МЕТОДА ДВУХ ЗАМЕН ПЛОСКОСТИ ПРОЕКЦИЙ К ПОЛУЧЕНИЮ НАГЛЯДНЫХ ИЗОБРАЖЕНИЙ
English version

|
Головнин Алексей Алексеевич | (Тверской государственный технический университет) |
| Казичев Игорь Николаевич | (Тверской государственный технический университет) |
Аннотация
Предложено при рассмотрении одной из центральных тем учебного курса начертательной геометрии – преобразования комплексного чертежа применять метод двух замен плоскостей проекций для получения наглядных изображений.
Ключевые слова: начертательная геометрия, наглядные изображения, метод замены плоскостей проекций
Преобразование комплексного чертежа – одна из центральных тем учебного курса начертательной геометрии. Освоение студентами этой темы играет важную роль в развитии навыков свободного чтения и понимания комплексного чертежа.
Наиболее простой алгоритм, и в очередности изучения материалов темы он стоит первым, это – преобразование комплексного чертежа путем замены плоскости проекций. При этом на выбор новой плоскости проекций накладывается ограничение: она выбирается перпендикулярной к одной из исходных. Путем двух замен можно перейти к плоскостям проекций не перпендикулярным ни одной из исходных, т.е. имеющим произвольную ориентацию. В результате может быть определена действительная величина какой либо геометрической фигуры, или получено более полное (наглядное) ее изображение [1стр.60].
В учебном процессе метод нашел применение только для приведения прямых и плоскостей к положению уровня или проецирующему положению. Встречаются даже специальные названия этих преобразований как четыре основные [2] или четыре исходные [3] задачи преобразования комплексного чертежа. Применение метода замены плоскости проекций для получения наглядного изображения в учебном процессе не принято. Между тем, в некоторых случаях целесообразно применение в конструкторской документации именно наглядных изображений. Например, допускается применять в чертеже аксонометрические проекции по ГОСТ 2.317 в конструкторской документации для упаковывания [4,5].
Целью работы является показать возможные варианты применения в учебном курсе начертательной геометрии метода двух замен плоскостей проекций для получения наглядных изображений.
Наглядное изображение принято получать методом аксонометрических проекций [6]. Под наглядным изображением мы понимаем такой вид предмета, который дает наибольшее представление о его форме по сравнению с любым из основных видов по ГОСТ 2.305. Будем отличать его от объемного изображения, под которым можно понимать воксельное, голографическое, стереоизображение и другие [7]. Кроме того лишь упомянем о существовании изображений, получаемых методами трёхмерной графики [8], обладающих существенно большей наглядностью по сравнению с получаемыми методами начертательной геометрии.
Правила построения наиболее наглядного изображения для аксонометрической проекции включают выбор вида аксонометрической проекции (с учетом того, что наиболее наглядные изображения дают аксонометрические прямоугольные триметрические проекции), расположение предмета относительно направления проектирования, отнесение предмета к системе прямоугольных осей координат, построение аксонометрических осей и непосредственное построение аксонометрической проекции предмета [6, Стр 249]. Можно заметить, что стремление к наглядности при выборе вида аксонометрии приходит в противоречие со стремлением к простоте построений, упор на которую просматривается в случае применения прямоугольных изометрии и диметрии, или косоугольных проекций по ГОСТ 2.317.
Известно также, что аксонометрическая проекция предмета может быть построена непосредственно по любым двум его ортогональным проекциям, а не по вторичным проекциям [6, c. 256]. По известному алгоритму для этого нужно определить для данного расположения аксонометрических осей направление, которое они имеют в совмещенном с картинной плоскостью положении, расположить ортогональные проекции, руководствуясь найденным направлением совмещенных осей, и найти аксонометрические проекции точек предмета в пересечении прямых, которые проводятся через ортогональные проекции этих точек параллельно соответствующим аксонометрическим осям.
Вместе с тем для получения наглядных изображений может быть применен метод двух замен плоскостей проекций [9, с.26]. На рисунке 2 на примере чертежа учебного задания в виде домика, заданного его двумя основными видами, показано, как после замены одной плоскости проекций в направлении по стрелке А, направленной горизонтально, можно получить вид на ребро с точкой 4. При этом становятся видны сразу две боковые стороны домика. Если на полученный вид посмотреть по стрелке Б, сверху вниз под наклоном на точку 3, то получим вид, на котором видны сразу две боковые стороны домика и его крыша, как это было бы, если бы построения велись с помощью измерений по осям и применением коэффициентов искажения по осям методом, привычным из темы аксонометрия учебного курса начертательной геометрии. После каждой из двух замен плоскости проекций полученное изображение можно довернуть путем плоско-параллельного переноса до привычного расположения, когда вертикаль на чертеже сохраняет свое положение, а можно не поворачивать, как принято при использовании метода замены плоскостей проекций. На рисунке 2 виды А и Б показаны дважды, в том положении, котором они получаются непосредственно после замены (в том, в котором мы привыкли видеть комплексные чертежи после их преобразований) и в довернутом положении (привычном из физических представлений, когда вертикальные линии на чертеже направлены снизу вверх). Применительно к учебным заданиям, нами использовались оба варианта. Полученное изображение обеспечивает наглядность, которая свойственна аксонометрическим проекциям, а именно прямоугольной триметрии. Описанный метод получения наглядного изображения не завязан ни на одну из пяти изометрий или диметрий по ГОСТ 2.317 и не требует применения показателей искажения, более того, можно не знать и вообще не думать о численных значений масштабных коэффициентов по осям. Нам представляется, что выбрать направление, в направлении которого будет получено наиболее наглядное изображение более естественно, чем выбирать, пусть по имеющимся, прошедшим проверку временем, рекомендациям одну из стандартных аксонометрий, определенных, очевидно из соображений простоты масштабов по осям для удобного устного счета. Более того, с ориентацией на работу в последующем с электронными моделями [10], более востребованным должен быть именно навык по выбору направления взгляда, который реализуется при визуализации (отображении) модели на электронном устройстве (например, экране дисплея). Кроме того, триметрии неизбежно должны занять более достойное место в практическом применении аксонометрии в связи с узакониванием возможности получения наглядного изображения «путем проецирования электронной модели изделия на плоскость» [11].
Можно заметить, что в процессе получения наглядного изображения мы не использовали атрибуты теории аксонометрии – аксонометрические оси, вторичная проекция, картинная плоскость, родство и другие. Из осторожности не применяем к полученному изображению термин аксонометрическая проекция, хотя очевидно оно обладает ее внешними признаками.
По сравнению с известным способом в наших построениях отсутствует обоснованный выбор направления аксонометрических осей. В результате вид полученных изображений определяется выбранными направлениями для замены исходных проекций. Непривычно и расположение оси z, которая должна быть вертикальна, что связано с нашим автоматическим восприятием гравитации от вестибулярного аппарата и от каждой клетки. Преодолеть это можно путем поворота исходных проекций, но использование в учебных целях полученных изображений, может дополнительно способствовать выработке и развитию понимания комплексного чертежа.
Хотя основное назначение аксонометрических проекций – повышенная наглядность, метричность полученных изображений может быть поддержана лучевым масштабом, дающим линейные масштабы для осей [6, стр. 251]. Другой вариант придания метричности наглядному изображению для оси z показан на рисунке 2, для других осей может быть аналогичной.
Выводы и предложения:
1. В статье показана возможность применения в учебном курсе начертательной геометрии метода двух замен плоскостей проекций для получения наглядных изображений.
2. Предлагается при рассмотрении одной из центральных тем учебного курса начертательной геометрии, играющего важную роль в развитии навыков свободного чтения и понимания комплексного чертежа, – преобразования комплексного чертежа, применять метод двух замен плоскостей проекций для получения наглядных изображений.
3. Приведен пример выполнения учебного задания по применению метода двух замен плоскостей проекций для получения наглядного изображения.
Список литературы
- Фролов С.А. Начертательная геометрия: Учебник для втузов.- 2-е изд., перераб. и доп. – М.: Машиностроение, 1983. – 240 с., ил.
- Способы преобразования чертежа: методические указания к выполнению эпюра № 2 (для студентов технических специальностей) / Юго-Зап. гос. ун-т; Сост.: С.И. Иванова, А.С. Белозеров. Курск, 2014. 31 с.: ил. 28, табл. 1. Библиогр.: с 31. https://swsu.ru/structura/up/fsa/kafedra_agg/literatura/mu_epur2.pdf
- Четыре исходных задачи преобразования чертежа. https://studopedia.su/14_80903_chetire-ishodnih-zadachi-preobrazovaniya-chertezha.html
- ГОСТ 2.418-2008 ЕСКД. Правила выполнения конструкторской документации для упаковывания.
- http://korobkaplus.ru/wp-content/uploads/2018/06/%D1%81%D0%B0%D0%BC%D0%BE%D1%81%D0%B1%D0%BE%D1%80%D0%BD%D1%8B%D0%B9-%D0%B3%D0%BE%D1%84%D1%80%D0%BE%D0%BF%D0%BE%D0%B4%D0%B4%D0%BE%D0%BD-%D1%81-%D0%BA%D1%80%D1%8B%D1%88%D0%BA%D0%BE%D0%B9.gif
- Глазунов Е.А., Четверухин Н.Ф. Аксонометрия: Учебное пособие. – М.: Государственное издательство технико-теоретической литературы, 1953. – 293 с., ил.
- Объемное изображение. https://skanvordoff.ru/query/empty/%D0%BE%D0%B1%D1%8A%D0%B5%D0%BC%D0%BD%D0%BE%D0%B5%20%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5
- Трёхмерная графика. https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D1%91%D1%85%D0%BC%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA%D0%B0
- Григорьев, В. Г. Инженерная графика : учеб. пособие / Григорьев В.Г., Горячев В.И., Головнин А.А. - Тверь : Ч. 1: Геометрические основы конструирования. - 2001. - 143 с. : ил.
- ГОСТ 2.052-2006. ЕСКД Электронная модель изделия.
- ГОСТ 2.317-2011. ЕСКД. Аксонометрические проекции.
Рисунки к докладу
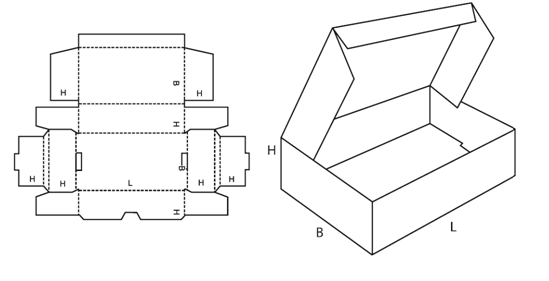
Рис. 1 Чертеж картонной коробки
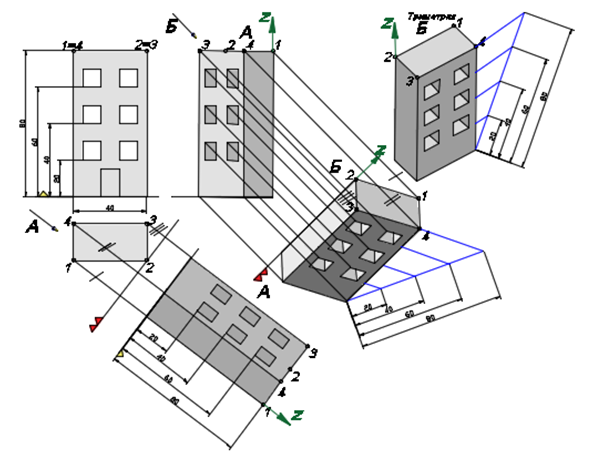
Рис. 2 Пример чертежа учебного задания
Вопросы и комментарии к выступлению:

Хейфец Александр Львович (10 марта 2019 г. 10:25) |
Алексей Алексеевич, здравствуйте. Вы предложили новый подход или способ построения аксономерии. Во первых, не отказывайтес от этого термина - у вас речь об аксонометрии. Способ, по моему, оригинален и позволит в теме замены плоскостей проекций сразу дать и основу аксонометрии. У Вас все четко и мне понятно изложено. Особенно важно, что времени на теорию аксонометрии в курсе НГ нам не осталось. Хорошо бы еще предварительно вспомнить о теореме Польке-Шварца. Только вот... Творческий интерес - это святое, это двигатель всего. У Вас он возник к этой теме - и я рад за Вас. Сам испытываю часто такой интерес к задачам, которые, как бы помягче, неактуальны. Действитеьльно, и Вы сами это понимаете, средства КГ позволяют наглядно построить любую и в том числе оптимальную аксонометрию - триметрию. С уважением. А.Л. Хейфец |

Головнин Алексей Алексеевич (10 марта 2019 г. 15:11) |
Здравствуйте Александр Львович! Спасибо за внимание к докладу. Я очень дорожу Вашим мнением. Для меня также важна Ваша оценка, что это - новое в аксонометрии. Сам прогонял такие мысли. При написании статьи искал в доступной литературе, что это уже было, нашел много нового для себя, даже похожего, при этом испытал что-то вроде восторга, но такого же подхода не нашел. Нам представляется, что это задание в большей мере учит навыкам работы с двухпроекционным чертежом, чем некоторые темы, в которых применяются хорошо заформализованные приемы типа метода секущих плоскостей например. Из истории вопроса. В конце 90-х моим старшим товарищем и учителем Валентином Георгиевичем Григорьевым было разработано графическое задание, в котором делалось до пяти замен плоскостей проекций, на последней высверливалось отверстие, которое потом возвращалось на исходные проекции. В 2001 году было издано учебное пособие, в котором основное внимание уделялось понятию вида. Вся кафедра была одержима таким подходом. И.Н.Казичев сохранил это задание и применяет его до сих пор. Видя их, возникла ассоциация с аксонометрией и в результате появилась эта работа. По поводу необходимости ссылки на теорему Польке-Шварца. Я не сразу ответил на Ваше замечание. Долго проверял и перепроверял. Ведь теорема Польке Шварца, тем более, что это теорема об аксонометрии, должна иметь доказательство путем замены плоскостей проекций. А именно путем двух замен может быть получена необходимая пропорция деления каждой из диагоналей четырехугольника от проецирования тетраэдра. Вторая часть теоремы может быть оставлена без изменений, а может быть быть также применена замена плоскостей проекций. В том изложении теоремы Польке-Шварца, на которое я опираюсь (Маневич, Котов, Зенгин. Аналитическая геометрия с теорией изображений), во второй части теоремы просто констатируется существование нужной плоскости. Может быть у Вас это получится раньше. Получится доказательство Хейфеца-Головнина. Это для поднятия настроения. Собственно только ради такого плодотворного общения лично я каждый год участвую в этой конференции. И не надо тратить времени, если собеседник не готов к полезному общению. И еще о неактуальности темы. Это известный закон развития техники, а может не только, - перед концом достигается совершенство. И еще, понравилось высказывание Александра Олеговича (примерно) - если бы что-то было бы не нужно, мы бы не обсуждали. В завершение как заклинание - надо переходить на геометрическое моделирование по пути самарцев. С уважением и благодарностью за общение Головнин А.А.
|

Хейфец Александр Львович (10 марта 2019 г. 19:31) |
Алексей Алексеевич, дать новое доказательство теоремы Польке-Шварца - задача заманчивая. Похоже, она у Вас на основе нового предложенного Вами подхода построения аксонометрии может получиться. От себя добавлю, что по этой теореме я опубликовал две объемные статьи. Посмотрите, может пригодятся и заинтересуют. Их легко вызвать по приведенным ссылкам: 1. А.Л. Хейфец. 3D-алгоритмы теоремы Польке-Шварца \ Вестник Южно-Уральского государственного университета. Серия “Строительство и архитектура”. – Челябинск: Изд-во ЮУрГУ. 2013. – Т. 13. №1, с. 71–80. https://vestnik.susu.ru/building/article/view/400/381 2. А.Л. Хейфец. 3D модели и алгоритмы компьютерной параметризации при решении задач конструктивной геометрии (на некоторых исторических примерах) \ Вестник Южно-Уральского государственного университета. Серия “Компьютерные технологии, управление, радиоэлектроника”. – Челябинск: Изд-во ЮУрГУ. 2016. – Т. 16. №2, с. 24–42. https://vestnik.susu.ru/ctcr/article/view/4909/4293 В 1-ой приведены все известные мне алгоритмы доказательства и применения теоремы и сравнительная оценка сложности их реализации. Во 2-й показана реализация ряда классических задач, в том числе теоремы Польке-Шварца, средствами современной КГ.
Готов продолжить общение на эту заманчивую тему.
С уважением. А.Л. Хейфец.
|

Полубинская Людмила Георгиевна (11 марта 2019 г. 15:34) |
Здравствуйте, уважаемые Алексей Алексеевич и Игорь Николаевич! С большим интересом и вниманием прочитала вашу статью. Абсолютно согласна с вашим мнением относительно роли преобразований в развитии навыков свободного чтения и понимания комплексного чертежа. Позвольте возразить или высказать своё мнение. Во-первых, преобразование чертежа. Это какой-то годами применяемый термин, шаблон, устойчивое словосочетание. Мне всегда хочется возразить - мы преобразуем не чертёж, мы преобразуем 3-хмерное пространство и получаем на двумерном носителе отображение этих преобразований. Изменяем одну пользовательскую систему координат на другую – ЗПП. Или в неизменной системе координат изменяем положение заданных объектов, используя вращение вокруг выбранной оси или плоскопараллельное перемещение, что по сути то же вращение вокруг проецирующей оси, неявно заданной. (Кстати, в американских учебниках показаны задачи, где используют и 3 и 4 замены, что и не рационально, и не лучшим образом сказывается на точности решения) А что касается перпендикулярности 2-х плоскостей проекций – так это условие заложено в метод, основоположником которого является Г.Монж. Во-вторых, немножко «с ног на голову» - эта тема не может рассматриваться без полного и уверенного усвоения студентом темы «Взаимное положение прямой и плоскости, 2-х плоскостей», т.к. без этого студент не может осознать ни цель преобразования, ни средства, ни полученный результат. Остаётся только формальное - откладываем этот отрезок на этой прямой. Честно говоря, я не поняла Рис. 1 Чертеж картонной коробки. Если это чертёж развёртки картонной коробки, то не совсем понятна «свёртка». И аксонометрия что-то мне не помогает. ГОСТ 2.418-2008. Правила выполнения конструкторской документации для упаковывания не позволяет нарушать ГОСТ 2.303-68 Линии. Статья интересная и вызывает желание продолжить разговор о наглядных изображениях и в НГ вообще, и об аксонометриях и о 3D. С уважением, Л.Г.Полубинская P.S Вообще, очень интересно обмениваться письмами, встречаясь чуть ни каждый день в стенах кафедры.
|
Назад Go Back
