АБСТРАКТНЫЕ МНОГОМЕРНЫЕ ПРОСТРАНСТВА В ИНЖЕНЕРНОМ ОБРАЗОВАНИИ
English version| Соколова Людмила Сергеевна | (Московский государственный технический университет им. Н.Э. Баумана) |
Аннотация
Рассматриваются содержание и использование понятий евклидова многомерного пространства и n-мерной наглядной геометрии в инженерном образовании. Представлены основные понятия многомерной геометрии: размерность пространства, степени свободы подпространств и параметрические свойства объектов. Приведены примеры использования понятия многомерного пространства в общеинженерных дисциплинах, изучаемых в высших технических учебных заведениях и формирующих знания современного инженера..
Ключевые слова: евклидово многомерное пространство, наглядная многомерная геометрия, общеинженерные дисциплины.
В результате обобщения понятия пространства термин «пространство» получает в науке два значения: с одной стороны, это - обычное реальное пространство - универсальная форма существования материи; с другой стороны, это - абстрактное пространство - совокупность однородных объектов (явлений, состояний и т.п.), в котором имеются пространственно-подобные отношения [1].
В реальном пространстве не существует представления о пространстве «самом по себе», пространстве без материи, так как «абсолютно» пустое пространство превращается в ничто. «Пустого» абстрактного пространства также не бывает. Разнообразию возможных совокупностей объектов и различных отношений между ними отвечает неограниченное разнообразие пространств.
Принятое в современной геометрии определение понятия пространства и фигуры исходит из понятия множества. Пространство определяется как множество каких-либо элементов (точек) с условием, что в этом множестве установлены некоторые соотношения, сходные с обычными пространственными отношениями. Фигура определяется как произвольное множество точек в одном пространстве.
Пространство оказывается евклидовым с достаточной точностью в областях, малых в сравнении с космическими масштабами. Вся техника, поскольку в ней фигурируют формы и размеры тел, пользуется евклидовой геометрией, дополненной декартовой системой координат. Поэтому пространства космического масштаба и другие неевклидовые, а тем более реальное физическое пространство, в данной работе не рассматриваются.
Общее реальное основание для введения понятия многомерного пространства основывается на том положении, что если какая-либо фигура, или состояние какой-либо системы задается n данными, то эту фигуру, это состояние можно представить как точку некоторого n-мерного пространства. Таким образом, множество всех точек М(Х1, Х2, ..., Хn) при всевозможных действительных значениях координат называют n-мерным пространством. Фигура в n-мерном пространстве - это геометрическое место или множество точек, удовлетворяющих тем или иным условиям. Например, ”n-мерный шар" определяется как множество точек, удаленных от данной не далее, чем на заданное расстояние R.
Абстрактность понятия многомерного пространства подчеркивается тем, что в n-мерной геометрии все подпространства принято называть плоскостями с указанием их размерности. Например, точка - это 0-плоскость с размерностью 0; прямая - это 1-плосткость с размерностью 1; обычная плоскость - это 2-плоскость с размерностью 2; трехмерное пространство - это 3-плоскость с размерностью 3 и т.п. При этом, каждая р-плоскость, где p<n, определяется заданием (р+1) точки и полностью принадлежит n-плоскости (n-мерному пространству). Эти р-плоскости называются линейными подпространствами многомерного (n-мерного) пространства.
Наиболее широкое применение понятие абстрактного пространства находит в самой геометрии. Геометрия многомерного пространства строилась сначала путем формального обобщения обычной аналитической геометрии на произвольное число измерений. Геометрический подход к изложению n-мерной геометрии, разработан Шлефли на примере правильных многогранников многомерного пространства. Обобщен сам геометрический метод исследования вне зависимости от аналитического аппарата, что придало ему реальную наглядность.
Выведено математическое определение абстрактного n-мерного декартового пространства, которое обозначается как Rn. Число n называется размерностью пространства или числом измерений и соответствует числу независимых координат. Таким образом, простейшими геометрическими фигурами размерностей 0, 1, 2, 3, 4 являются соответственно точка (R0), отрезок (R1), треугольник (R2), тетраэдр (R3), четырехмерный симплекс (R4). Такой подход в наиболее полной мере отвечает понятию наглядности в многомерной геометрии, что делает её более доступной для понимания при изучении [6,8].
Многомерная геометрия естественным образом объединяет в себе такие понятия как размерность пространства, степени свободы и параметры геометрической фигуры. Размерностью пространства в математике называют число независимых координат, в механике - число степеней свободы, в конструктивной геометрии - число независимых параметров. Тогда, принимая точку за основной элемент пространства, говорят, что на прямой (одномерное пространство) точка определяется заданием одной координаты, имеет одну степень свободы и один параметр; на плоскости (двумерное пространство) -двумя координатами, двумя степенями свободы и двумя параметрами; в трехмерном пространстве - тремя координатами, тремя степенями свободы и тремя параметрами и т.п.[3].
Приведем некоторые примеры использования понятия многомерного пространства в общеинженерных дисциплинах, изучаемых во втузах.
В инженерной геометрии при решении прикладных задач определяют по известным формулам [3] для i подпространств размерностями p1, p2, …,pi размерность вмещающего (содержащего) их пространства (n ) и пространства пересечения (r ). Например, плоскость (p2=2) и трехмерное пространство (p3=3) не имеют общих точек, т.е. будут скрещиваюшимися, если принадлежат пространству, размерность n которого не ниже, чем n=p2+p3+i-1=2+3+2-1=6, а размерность r пространства пересечения – отрицательна r=p2+p3-n(i-1)=2+3-6(2-1)=-1
Метод подсчета параметров – параметризация – широко применяется в разных областях науки и техники. Под параметражем геометрических фигур понимают способы, процесс и результат подсчета числа независимых параметров, определяющих фигуру по форме и по положению ее в пространстве среди множества соответствующих фигур. Например, чтобы задать некую окружность на плоскости необходимо задать три ее параметра (P ): радиус и две координаты ее центра, т.е. P=3. Если таких окружностей, например, три (N=3), то необходимо задать P=3N параметров, т.е. P=3x3=9 независимых параметров. Это определит размерность n операционного пространства для их размещения, равную n=P, т.е n=9 (9-мерное пространство). Для задания шара необходимо задать его радиус и три координаты центра, всего 4 независимых параметра. Тогда для трех независимых шаров (N=3) потребуется задать P= 4x3=12 независимых параметров. Размерность n операционного пространства для их размещения, равная числу независимых параметров P , составит n=12 (12-мерное пространство).
В учебном курсе теоретической механики изучается механическое движение. В евклидовом пространстве, дополненном тремя декартовыми координатами, изучается обычное мезаническое движени твердых тел. При задании движения твердого тела в механике его положение в пространстве считают определенным, если известно положение трех его базисных точек, не лежащих на одной прямой и неизменно связанных с телом. Поскольку на девять координат этих трех точек наложено три ограничения, выражающих неизменность расстояния между точками, то число независимых координат, задающих положение свободного тела в пространстве, а значит и число степеней его свободы равно шести. Движение такого тела, в общем случае может быть всегда представлено как вращение вокруг и перемещение вдоль трех произвольно выбранных взаимно перпендикулярных осей.
В общем случае движения твердого тела можно говорить об абстрактном шестимерном пространстве R6 как о пространстве размерностью n=6, где может осуществляться это движение. Фиксируя некоторые координаты, можно воспроизводить различные частные случаи движения тела с меньшим числом степеней свободы, т.е. в пространстве меньшей размерности. Другой вариант сокращения числа степеней свободы движения твердого тела является установление какой-либо функциональной зависимости между двумя или несколькими обобщенными координатами. Использование современного числового программного управления позволяет организовать движение тела (например, режущего инструмента) по заданной траектории, т.е. в абстрактном одномерном пространстве многокоординатного станка ( рис.1 ).
Идеи многомерной геометрии нашли применение и в курсе такой общеинженерной дисциплины как "Теория механизмов и машин", общие методы которой используются также в курсах "Детали машин", "Детали приборов" в применении к конкретным механизмам. Они основаны на тех закономерностях в структуре (строении) самых различных механизмов, которые связывают число степеней свободы (обозначается как W) механизма с числом звеньев и числом и видом его кинематических пар[10]. Эта величина W и будет определять размерность операционного пространства, т.е. пространства, в котором изучается созданный механизм.
Рассмотрим конкретную задачу, решаемую в робототехнике при проектировании и управлении промышленными роботами. Задача заимствована из [10, лекция 24, рис. 24.2 с разрешения автора].
В процессе выполнения операции с объектами в большинстве случаев манипуляторы имитируют движение рук человека. Поэтому структурная схема манипулятора должна обладать кинематическими характеристиками, аналогичными характеристикам руки человека (рис. 2). Подвижности имеющиеся у руки человека (без учета подвижности пальцев) можно обеспечить с помощью пространственной кинематической цепи, состоящей из N = 3 звеньев: А с подвижностью WA = 3; В с WB = 1; и С с WС = 3.
Тогда, число степеней свободы данного пространственного механизма (W) определяется как
W = WA+WВ+Wс = 3+1+3 =7
Размерность операционного пространства, содержащего исследуемый механизм, согласно представлениям многомерной геометрии, равна числу независимых координат механизма, т.е. числу независимых степеней свободы. Поэтому размерность рассматриваемого пространства Rn равна n = W = 7 и зависит только от конструкции механизма. С учетом всех звеньев и в самой кисти имели бы W = 27, т.е. абстрактное операционное пространство R27 с 27-ю степенями свободы. Такое многомерное пространство становится вполне наглядным, исходя из схемы конструкции и логики ее создания, а также представлений многомерной геометрии (см. рис2).
Ещё один пример, уже из области метрологии [4].
Если ранее измерение и контроль трехмерных объектов основывался на измерении сечений, то сегодня многие доступные CАD и системы анализа представляют интерфейс для массива точек, содержащего, например, до N = 1300000 точек, который служит выходными данными систем оцифровки. Современные КИМ (контрольно-измерительные машины) измеряют одновременно в трех декартовых координатах, а технология сканирования позволяет за один раз захватывать 1000 и более точек. В этом методе первоисточником является трехмерная электронная модель объекта.
Таким образом, размерность пространства контролируемой поверхности изделия дает представление о Р =3N-мерном абстрактном пространстве R3N, где N может достигать 1300000 контролируемых точек. Данные могут быть представлены в виде таблиц, диаграмм, графиков с визуальным показом положения и значений отклонений всех независимых координат. Наглядность представленного такого многомерного контролируемого пространства совершенно очевидна.
Абстрактное пространство может даже мало походить на обычное пространство. Известно, что в кинетической теории газов рассматривают абстрактные, так называемые "фазовые пространства" системы материальных точек - молекул газа (пример из [1]). Движение одной частицы в каждый момент определяется ее положением и скоростью, что дает всего шесть величин: три координаты и три составляющие скорости (по трем осям координат). Состояние N частиц задается 6N величинами и так как молекул много, то 6N - огромное число. Тем не менее, физики говорят о 6N-мерном фазовом пространстве системы молекул. Точка в этом пространстве изображает состояние всей массы молекул с их координатами и скоростями. Движение точки изображает изменение состояния.
Анализ вышеприведенных примеров показывает, что такие основные понятия многомерной геометрии как размерность пространств, число степеней свободы и параметризация геометрических фигур и условий давно известны, и естественно, изучаются в общеинженерных дисциплинах высших технических учебных заведений в применениях к конкретным наукам. Это позволяет на обобщающем примере из геометрии показать, как получаются наглядные изображения многомерного евклидова пространства RP разной размерности (Р).
Рассмотрим твердое тело в системе n декартовых координат Хn (рис. 3). Твердым телом или неизменяемой системой называют такую механическую систему, которая состоит из множества материальных точек, заполняющих сплошным образом некоторую часть пространства. Основным свойством твердого тела является неизменность расстояний между любыми двумя точками. Движение такого тела возможно только в евклидовом пространстве.
Точка в многомерном пространстве определяется n декартовыми координатами Х1, Х2, ..., Хn. На рис.3 представлены четыре координатные системы с декартовыми координатами Х1; Х1, Х2; Х1, Х2,Х3; Х1, Х2, Х3, Х4 (см.а, б, в, г соответственно). Поскольку в n-мерной геометрии число точек, задающих р-плоскость в системе с n координатами принимают на единицу больше числа координат (n), число базисных точек твердого тела N = n + 1.
Параметраж геометрической фигуры в данном случае позволяет прямым подсчетом выявить число наложенных на систему геометрических связей (s) и определить тем самым число независимых между собой параметров среди общего числа параметров равного n∙N. Это число независимых параметров (за вычетом наложенных геометрических связей) определяет и размерность пространства и число степеней свободы (Р) в данном пространстве согласно универсальной зависимости
Р = n∙N - s , (1)
где Р - размерность пространства, это же - число степеней свободы, это же - параметрическое число;
Результаты расчета представлены таблицей на рис. 3.
Размерность абстрактного пространства RP равна числу существующих в нем независимых параметров (Р), являющихся его координатами. В механике таким независимым координатам соответствует число степеней свободы, т.е. число независимых между собой возможных перемещений. Из таблицы на рис.3 видно, какие и сколько перемещений может осуществляться в рассматриваемых четырех системах координат. Таким образом многомерное евклидово пространство может быть наглядно изображено и доступно для понимания, исходя из логики его образования и простых понятий многомерной геометрии.
Представленный материал показывает, как именно в технике нашло применение понятия абстрактного пространства. Абстрактное пространство - это не пустое пространство, а то. что в нем содержится, т.е. его наполнение разным содержанием. Содержание абстрактного пространства в инженерной практике - это разного рода конструкции, разные формы взаимодействующих объектов, их перемещения и др., т.е. вполне реальные действия, а не экзотическая игра ума.
Очень важным представляется мнение акад. А.Д. Александрова, в котором он отмечает, что "... до студентов должна быть доведена идея о том, что понятие абстрактного пространства имеет вполне реальное основание, оно отражает действительность и было вызвано потребностями науки, а не праздной игрой воображения..." и, как мы видим, доведено до технических применений.
Такой подход позволяет поставить вопрос о целесообразности использования наглядной многомерной геометрии в общеинженерном техническом образовании в качестве междисциплинарного базового курса.
Это дает полное основание для введения в программы кафедр инженерной графики пропедевтического курса наглядной многомерной геометрии в составе предлагаемой дисциплины "Наглядная инженерная геометрия" [5,7], что позволит кафедрам инженерной графики сохранить геометрию в качестве научного направления в своей деятельности в условиях перехода на современные информационные технологии, когда создание электронной модели заменяет собой создание двухкартинного чертежа Монжа.
В [6] представлены материалы, показывающие возможность совместного выстраивания наглядной геометрии и понятия многомерного пространства в учебной программе по геометрической подготовке студентов.
Обновление программ по геометро-графической подготовке для бакалавриата технического университета в предложенном виде позволит обеспечить междисциплинарные связи не только с кафедрами профессиональной подготовки, но и с кафедрами общеинженерных дисциплин, а также межвузовские связи. Это отвечает ведущим тенденциям в потребности инженерной подготовки и встраиванию предметного обучения в компетентностную модель подготовки будущего инженера [2,9].
Список литературы
- Александров А.Д. Геометрия. БСЭ, М. 1971, №6, с.909-927.
- Горнов А.О., Лепаров М.Н. Системные противоречия и предпосылки инженерной геометрии в образовательном аспекте. Материалы VII Международной научно-практической конференции "Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации". Пермь, 2017, с.14-22. http://dgng.pstu.ru/conf2017/
- Иванов Г.С. Теоретические основы начертательной геометрии. Глава4.,М.1998,с.58-76
- Пекарш А.И. Феоктистов С.И. Колыхалов Д.Г., Шпорт В.И. Координатно-измерительные машины и комплексы / Статья в издании: "Международная энциклопедия CALS. Авиационно-космическое машиностроение"/ Гл. ред. А.Г. Братухин. М.:ОАО "НИЦ АСК", 2015, с.476-489.
- Соколова Л.С..Инженерная геометрия – новая учебная дисциплина по геометро-графической подготовке для высших технических учебных заведений. Инженерный журнал: наука и инновации. 2014,вып.3,с.7-11
- Соколова Л.С. Многомерное пространство и наглядная геометрия в учебной программе по геометрической подготовке бакалавров // Геометрия и графика, 2015, Том 3, вып.1 стр. 40-46.
- Соколова Л.С. Геометрическая подготовка бакалавров в современных условиях// Труды КГП – 2016, Пермь, 2016, вып. 3, с.326-332.
URL: http://dgng.pstu.ru/conf2016/ - Соколова Л.С. О наглядности в инженерной геометрии. Материалы VII Международной научно-практической конференции "Проблемы качества грфической подготовки студентов в техническом вузе: традиции и инновации".Пермь,2017, с.138-147.
URL: http://dgng.pstu.ru/conf2017/
- Столбова И.Д. Организация предметного обучения: компетентностный подход // Высшее образование в России. 2012 №7, с.10-20.
- Тимофеев Г.А. Теория механизмов и машин. Учебное пособие, базовый курс для бакалавров. М., 2-е издание, 2014, Юрайт, 351 с.
Рисунки к докладу
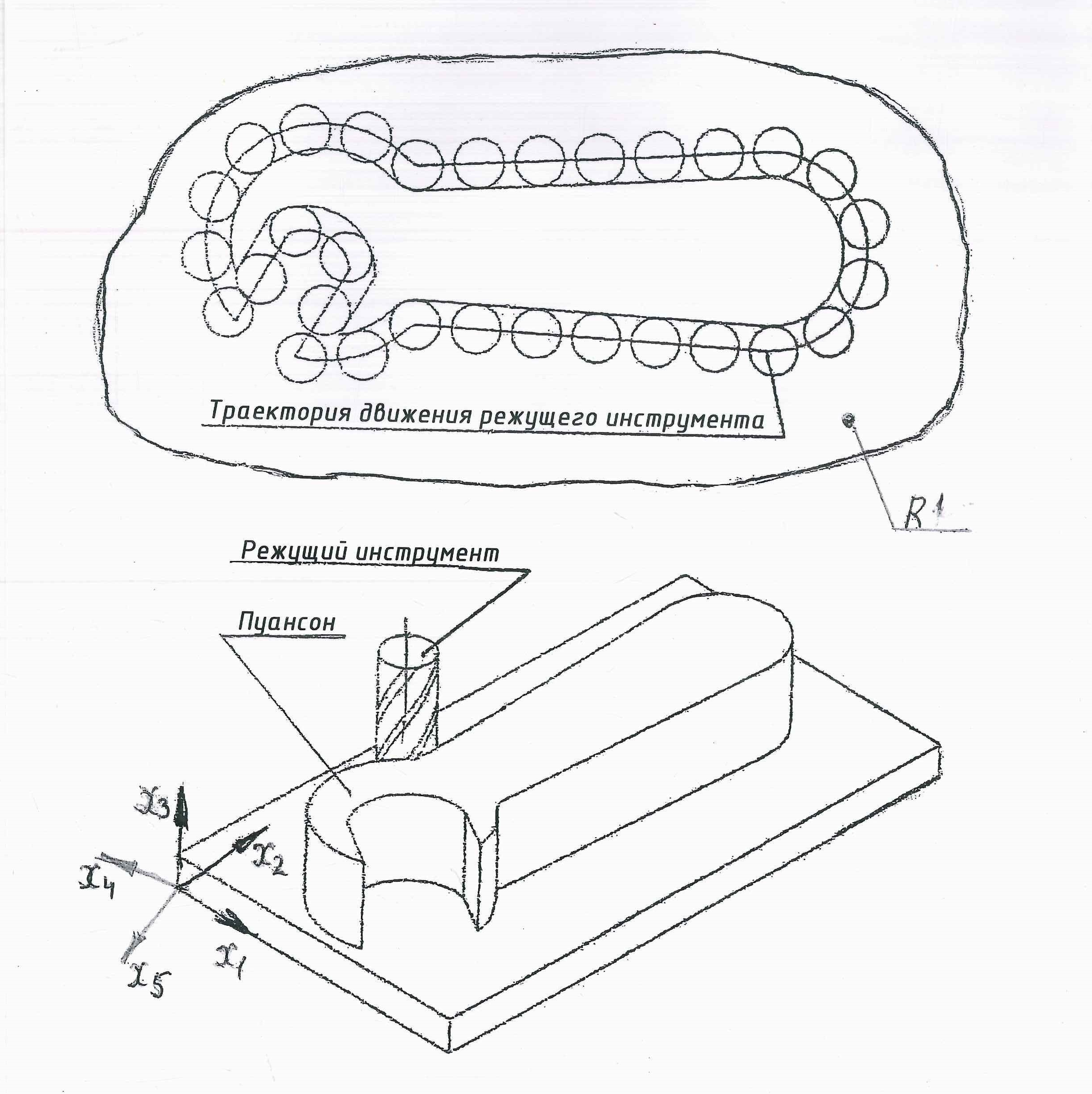
Рис. 1 Обработка пуансона на 5-координатном станке с числовым программным управлением. Размерность операционного пространства n=1 т.е. в одномерном пространстве R1
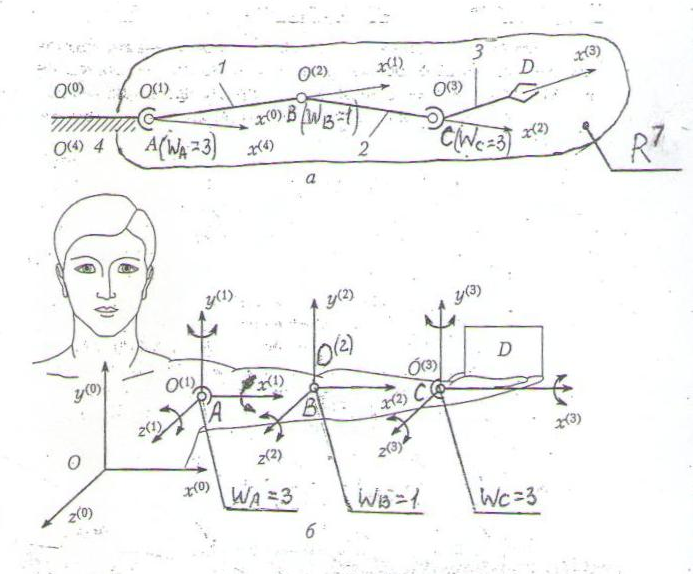
Рис. 2 Структурная схема (а) промышленного робота, имитирующего движение рук человека (б). Размерность операционного пространства, содержащего данный механизм, w=7, что соответствует R7(7-мерному пространству)
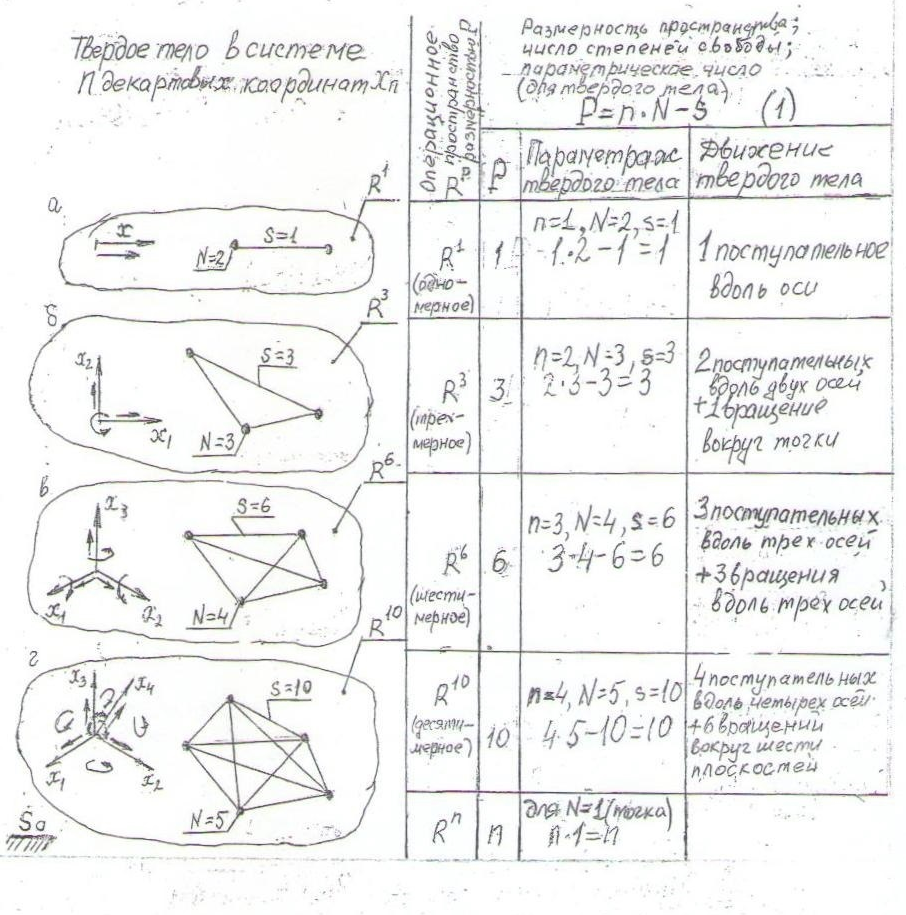
Рис. 3 Операционные пространства разной размерности RР для твердого тела в системе n декартовых координат Xn
Вопросы и комментарии к выступлению:

Селиверстов Александр Владиславович (26 февраля 2019 г. 13:45) |
Уважаемая Людмила Сергеевна! К сожалению, Ваш доклад далёк от НГ и графической подготовки. Мне бесполезно многомерное пространство, пока не научился работать в трёхмерном. Оставаясь же в трёхмерном пространстве, легко перекинуть "мостик" между геомерией и теорией механизмов и машин, говоря именно об абстрактном конфигурационном пространстве. Пример: плоский двухзвенный манипулятор, положение которого определяется двумя углами, то есть точкой на торе – поверхности в трёхмерном пространстве. Здесь полезно строить проекции и сечения тора. Если наложить некоторое ограничение, то конфигурации будут соответствовать точкам сечения тора. Дальше можно рассказать об окружностях Вилларсо. Кстати, про их обобщение пишет Антон Георгиевич Гирш в Journal for Geometry and Graphics. 2002. V.6. No.2. P.121–132. http://www.heldermann-verlag.de/jgg/jgg06/jgg0610.pdf Развивая пример, можно подняться настолько высоко, насколько готовы слушатели. И при этом сохранять геометрию, а не заменять её троянским конём, лишь украшенным ссылками на Александрова и уважаемых коллег. Имея опыт работы в (абстрактном) трёхмерном пространстве, легко перейти к многомерному. Но хорошая идея должна быть понята, а не заучена как заклинание. |
|
Соколова Людмила Сергеевна (28 февраля 2019 г. 14:31) |
Уважаемые коллеги! Обращаю Ваше внимание, что в моем докладе речь не идет о многомерной НГ, да и вообще о НГ.Л.С.Соколова |

Селиверстов Александр Владиславович (28 февраля 2019 г. 17:41) |
Здравствуйте, Людмила Сергеевна! |

Головнин Алексей Алексеевич (1 марта 2019 г. 12:22) |
Здравствуйте Людмила Сергеевна! С большим интересом знакомлюсь с Вашими работами. Они учат, что на известные и понятные вещи бывает полезно посмотреть свежим взглядом. Мне дорого то, что Вы накануне поделились со мной планами опубликовать такую работу. В ней, как я понял, Вы показываете, как известные научные факты и теории можно изложить в терминах многомерного пространства и n-мерной наглядной геометрии. В частности Вы предлагаете размерность пространства отожествить с числом степеней свободы. Возможно, такая трактовка была бы ближе нам, по долгу службы или даже по призванию, геометрам, но как отнесутся к этому представители смежных наук - теоретической механики, теории механизмов и машин, машиностроения и других областей науки и техники, в которых, число степеней свободы является фундаментальным и самодостаточным понятием. Есть очень простой критерий нужности «новой» теории – с ее помощью можно установить какой-то новый научный факт, не известный в «старой» теории. Навряд ли использование понятий евклидова многомерного пространства и n-мерной наглядной геометрии сможет быть полезным и в учебном процессе и в системе научных знаний будущих специалистов с высшим техническим образованием. Возможно многомерности – это область математики, но и здесь есть известный опыт В.А.Пеклича, когда он выходил за апробацией к математикам. В Вашем докладе я вижу повод вернуться к вопросу о том, что именно желательно успеть обсудить за время встречи, возможность которой нам в очередной раз любезно предоставили ее организаторы. Буквально в последние три дня прошлой конференции был поднят и активно обсуждался вопрос о том, что «у нас практически отсутствуют теоретические исследования в области геометромодельной подготовки» Было предложено «одну из секция или переименовать или создать новую «Теория и методика геометромодельной подготовки ...». Как вариант было предложено «с целью разработки современной концепции развития геометромодельной подготовки специалистов создать рабочую комиссию (или группу), на базе технического университета им. Баумана». Было предложено «организовать общественный орган для разработки концепции преподавания начертательной геометрии, инженерной и компьютерной графики в современных условиях (содержание, разумное сочетание внутрипредметных связей, программы, темы заданий и т.д.)» Возможно активное обсуждение этих вопросов на этой конференции еще впереди. С уважением Головнин А.А. |
|
Соколова Людмила Сергеевна (5 марта 2019 г. 16:46) |
Здравствуйте, Алексей Алексеевич! Спасибо на добром слове. Я хотела показать, что многомерную геометрию, степени свободы и параметризацию геометрических фигур объединяет одно понятие - абстрактное многомерное пространство. Мои примеры из Термеха, ТММ и др.ничего не меняют для этих самодостаточных наук, зато оправдывают использование многомерной геометрии в учебных программах кафедр "Инженерная графика" как общеинженерную дисциплину, вместе с тем оставляя за кафедрами геометрию в качестве научного направления в их деятельности. Л.С.Соколова |
Назад Go Back
