МЕТОДИКА РЕШЕНИЯ НЕЦИРКУЛЬНЫХ КОНСТРУКТИВНЫХ ЗАДАЧ
English version

|
Гайдарь Олег Георгиевич | (Донецкий национальный технический университет) |
Аннотация
В работе рассмотрена методология решения нециркульных линейчатых конструктивных задач содержащих одну гонометрическую или одну эквигональную связь.
Ключевые слова: конструктивная задача, нециркульная задача, гонометрические связи, эквигональные связи, проекции
Конструктивные задачи, наверное, самые древние в истории геометрии. Геометрическими построениями занимались почти все крупные древнегреческие геометры: Пифагор и его ученики, Гиппократ, Евклид, Архимед, Апполоний, Папп и многие другие. Много внимания уделяли конструктивным задачам творцы современной математики: Декарт, Ферма, Ньютон, Паскаль, Эйлер, Гаусс. В XVII-XIX веках разработана теория геометрических построений с помощью различных инструментов, отличных от принятых древними. Датчанин Мор (1672), итальянец Маскерони (1797), француз Понселёж (1813), швейцарец Штейнер (1833), немец Адлер изучали построения, выполнимые циркулем и линейкой, и обнаружили, что циркуль позволяет решить всякую конструктивную задачу, разрешимую циркулем и линейкой и наоборот – только с помощью линейки можно решить всякую циркульную задачу [1]. С конца XIX и по конец XX веков теория геометрических построений сформировалась в обширную и глубоко развитую область математики, связанную с решением разнообразных принципиальных вопросов, уходящих в другие ветви математики [1].
В работе [2] мы начали рассматривать конструктивные задачи с точки зрения компьютерной реализации их решения. Была проведена классификация конструктивных задач и выявлены их элементарные составляющие – симплексы. Показано, что таких симплексов для линейчатых конструктивных задач существует всего 10.
Все известные линейчатые конструктивные задачи можно свести к 344 задачам. Среди них 22 параметрических, 37 функциональных и 285 функционально-параметрических [2]. Разрешимы с помощью циркуля и линейки 143 задачи – такие задачи будем называть циркульными, остальные имеют степень уравнения выше второй, т.е. не могут быть решены с помощью циркуля и линейки – будем их называть не циркульными.
Признак, по которому можно определить, является ли задача циркульной или нет, заключается в следующем. Если в задаче есть две связи (функциональные, или параметрические, или одна функциональная, а другая параметрическая), зависящие от углов, то такая задача является циркульной.
Все представленные симплексы хорошо известны, но они позволяют решить только весьма ограниченные круг циркульных конструктивных задачи [3]. При этом остается не тронутым огромный пласт нециркульных задач. В этой работе разберёмся в методологии решения конструктивных задач 3-й и выше степени.
Нециркульные линейчатые конструктивные задачи могут содержать либо одну гонометрическую связь, либо одну эквигональную связь, либо не иметь угловой связи.
Каждый из этих трех типов задач имеет свою методику решений. В этой работе рассмотрим только первых два случая.
Пусть задача содержит одну гонометрическую связь. Например, в условии задачи: "Построить прямую х на расстояниях R1, R2 от точек А, В, под углом α к прямой с и равноудаленную от точек D, E - содержится одна гонометрическая связь. При решении таких задач следует выбрать дополнительную плоскость проекций П5, перпендикулярную оси конуса Ф. Конус Ф образован осью с и углом α наклона образующих mi к оси с. В данной конкретной задаче плоскость П5 должна быть перпендикулярной прямой с. Если в задаче сказано, что необходимо построить прямую х под углом α к плоскости ∑, то дополнительная плоскость проекций должна быть параллельна плоскости ∑. В этом случае ось конуса Ф будет перпендикулярна к П5. Угол β наклона образующих mi конца Ф к плоскости П5 будет равен 90°- α.
Проецируем на плоскость П5 конус Ф. Ось с конуса изобразится точкой c5, основание конуса Ф - в виде окружности К5. Основание К можно взять на любом расстоянии от вершины S. Вершина S назначается в произвольном месте прямой с. На плоскость П5 проецируем и остальные фигуры задачи (рис. 1а). В заданной конкретной задаче - точки А, В, D, Е. На окружности к назначаем ряд точек 1...n. На рис. 4 назначено 12 точек. Соединим точки 1...12 с вершиной S. Получим 12 образующих mi - S1...S12. Возьмем образующую S1 и преобразуем чертеж так, чтобы образующая S1 спроецировалась в точку (рис. 1б.). Окружности с центрами в точках А7 и В7 являются множествами прямых, перпендикулярных П7 (следовательно параллельных S1, так как S1 спроецировалась на П7 в точку S7 = I7. Окружности, пересекаясь в точках Р7 и R7, задают две прямые, удаленные от точек А и В на расстояния R1, R2 и параллельные S1. Соединим точки D7 и E7. Прямую D7E7 разделим пополам. Через середину D7E7 проведем прямую Г7, перпендикулярную D7E7. Прямая Г7 является перпендикулярной плоскости Г, перпендикулярной П7. Она содержит в себе прямые, перпендикулярные П7 и равноудаленные от точек D и Е. Заметим, что прямая DE в общем случае не перпендикулярна Г. Если же точки D и Е будут одинаково удалены от П7, то DE будет перпендикулярна Г. Когда Г7 пройдет через точку Р7 или R7, то точка Р7 или R7 будет проекцией искомой прямой х. Однако, как правило Г7 ни проходит ни через Р7 ни через R7. Между Г7 и Р7, Г7 и R7 отмечаем расстояния 1 и h.
Точно такие же операции проводим по направлению остальных 11 образующих конуса Ф. По результатам замеров Δ1 и Δh строим графики. По оси х откладываем отрезки 1-2, 2-3, ..., 12-1. По оси у - Δ1 и Δh. Условимся считать Δ1 и Δh положительными величинами, если Г7 ниже Pi и Ri, и отрицательными величинами, если Г7 выше Pi и Ri. Графики выполнены на рис. 2. Через точки, где графики пересекают ось х, пройдут искомые образующие х. В данном случае отмечены только две точки М и N. Разрыв графиков говорит о том, что окружности с центрами в точках А и В не пересекаются по данным направлениям. График Δh вообще не пересекает ось х. Поэтому для данной задачи существует только две искомые линии х. Обратным проецированием находим х на исходных проекциях. Пересечение графика Δ1 оси х говорит о том, что по данному направлению Гi пройдет через точки Pi и Ri.
Исследование. Количество решений задачи определяется количеством точек пересечения графиков Δ1 и Δh оси х и пересечением или касанием окружностей с центрами в точках А и В радиусов R1 и R2. Максимальное число решений равно 4. Также возможны 3, 2, 1 и 0 решений. Ноль решений будет, когда окружности не пересекаются (и не касаются), или графики Δ1 и Δh не пересекают оси х.
Рассмотрим методику решения конструктивных задач, в которых имеется одна эквигональная связь. Следует выделить здесь две группы задач.
К первой относятся задачи, в которых необходимо построить прямую х, равнонаклонную к двум прямым или двум плоскостям.
Ко второй - прямую х, равнонаклонную к прямой и плоскости. Изучим методику решения таких задач на конкретных примерах.
Пусть задана задача: "Построить прямую х на расстояниях R1, R2 от точек А, В, равноудаленную от точки С и прямой d и равнонаклонную к прямым е и q".
Анализ. Множеством прямых, удаленных от точки А на расстояния R1, и от точки В на расстояние R2 будет конгруэнция прямых, фокальными поверхностями которых являются сферы с центрами в точках А и В и радиусами соответственно R1 и R2. Другими словами, это множество состоит из прямых касательных к вышеупомянутым сферам. Оно включает в себя два конуса (или один конус и один цилиндр, если R1 = R2) и однопараметрическое множество однополостных гиперболоидов.
Множество прямых, равноудаленных от точки С и прямой d будет комплекс прямых, касательных к сферам с центром в точке С и цилиндрам с осью d, радиусы которых попарно одинаково изменяются. Это множество заполняет все пространство.
Множество прямых, равнонаклонных к прямым е и q, представляют собой две плоскости ∑ и Г и прямые пространства, параллельные плоскостям ∑ и Г. Плоскости ∑ и Г представляют собой биссекторные плоскости углов, образованные двумя пересекающимися прямыми е1 и q1, параллельными соответственно прямым е и q. Задать плоскости ∑ и Г можно следующим образом. Возьмем произвольную точку S.
Проведем через нее две прямые е1 и q1, параллельные соответственно прямым е и q. Разделим углы, образованные прямыми е1 и q1, пополам прямыми m и n. Из точки S восставим перпендикуляр р к плоскости Т, образованной прямыми е1 и q1. Биссектриса m и перпендикуляр р зададут плоскость Г, плоскость ∑ будет задана биссектрисой n и перпендикуляром р. Любая прямая 1, лежащая в плоскостях Г и ∑, будет равнонаклонна к прямым е1 и q1 и, следовательно, к прямым е и q.
В качестве дополнительной плоскости пересечения возьмем плоскость Г (затем плоскость ∑), или любую плоскость П5, параллельную Г. Спроецируем на плоскость Г (или П5) все фигуры задачи. Назначим в плоскости Г произвольную точку М и через нее проведем ряд прямых. Для этих целей удобно провести окружность произвольного радиуса с центром в точке М и разделить ее на равное число отрезков, например 12 (рис. 3).
Преобразуем чертеж так, чтобы прямая l1 спроецировалась в точку l17 . На плоскость П7 следует спроецировать и остальные фигуры задачи. На чертеже парабола t7 - множество прямых, равноудаленных от точки С и прямой d и параллельных l1. Окружности к17 и к117 - множество прямых, удаленных от А и В соответственно на расстояния R1 и R2 и параллельных прямой 1. Точки F7 и Н7 пересечения окружностей выделяет из последних двух множеств две прямые g и u, удаленные от А и В на расстояния R1 и R2 соответственно, и параллельные l1. Если бы парабола t7 прошла через одну из точек F7 или Н7, то задача была бы решена, так как одна из прямых g или u была бы искомой. Поэтому для нахождения искомой прямой х необходимо осуществить преобразования чертежа столько раз, сколько назначено прямых 1i (рис. 3). Во всех случаях надо добиться, чтобы прямая 1i спроецировалась в точку. На каждом чертеже будем замерять расстояния r1 и r11. Результаты замеров отложим на графике (рис. 4). По оси х отложим длины отрезков 1-2, 2-3, ..., 12-1, по оси у - отрезки r1 и r11. Условимся, если парабола расположена относительно точек Fi, Нi, слева, г1 и г11 - положительны, если справа - отрицательны.
На чертеже видно, что график расстояний r1 пересекает ось х в точках L и G. Если отметить точки L и G на рис. 3, то окажется, что линии ML и MG будут искомыми прямыми х, так как по направлению этих прямых парабола ti пройдет через точку Fi. На рис. 4б видно, что по всем направлениям парабола ti не проходит через точку Hi. По направлениям М10 и М11 овружности к1i и к11i не пересекаются.
Аналогичные построения следует выполнить теперь относительно плоскости ∑.
Исследование. Задача может иметь от нуля до восьми решений.
Множество прямых, равнонаклонных к двум плоскостям Δ и Λ, представляет собой две плоскости ∑ и Г и прямые пространства, параллельные плоскостям ∑ и Г. Плоскости ∑ и Г представляют собой две биссекторные плоскости углов, образованных плоскостями Δ и Λ. В задачах, в которых присутствует такая связь, дополнительные плоскости проекций следует назначать параллельными или совпадающими с плоскостями ∑ и Г.
Дальнейшие построения аналогичны построениям предыдущей задачи.
Изучим методику решения задач, в которых возникает необходимость построения прямой, равнонаклонной к прямой и плоскости.
Множество прямых, равнонаклонных к прямой и плоскости, представляют собой конус Ф и прямые пространства, параллельные образующим конуса Ф. Построение конуса Ф рассмотрено в п. 4 (симплекс 9) [2].
В задачах, в которых есть одна эквигональная связь на построение прямой, равнонаклонной к другой прямой и плоскости, необходимо в качестве дополнительной плоскости проекций назначить плоскость, ей параллельную. Провести на поверхности конуса Ф некоторое число образующих, например 12. И по направлению этих образующих спроецировать на плоскости, перпендикулярные им, все фигуры, входящие в задачу. Дополнительные построения аналогичны построениям в предыдущих задачах.
В работе рассмотрена методология решения нециркульных линейчатых конструктивных задач содержащих одну гонометрическую или одну эквигональную связь. В последующем необходимо завершить исследования методики решения задач, в которых отсутствуют условия связи.
Список литературы
1. Волошинов Д.В., Соломонов К.Н. Конструктивное геометрическое моделировавние как перспектива преподавания графических дисциплин // Геометрия и графика. - 2013. - Т. 1, вып. 2. - С. 182-185.
2. Гайдарь О.Г., Пастернак Д.Н. Классификация и структурирование линейчатых конструктивных задач применительно к компьютерному моделированию // Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации. Материалы VII Международной научно-практической конференции. Выпуск 4. Пермь, Из-во ПНИПУ 2017. С 203-210.
3. Гайдарь О.Г. Методика решения циркульных конструктивных задач // Инновационные перспективы Донбасса. Материалы 4-й Международной научно-практической конференции г. Донецк, 22-25 мая 2018 г. Т. 3: Инновационные технологии проектирования, изготовления и эксплуатации промышленных машин и агрегатов – Донецк: ДонНТУ, 2018. С. 16-20.
Рисунки к докладу
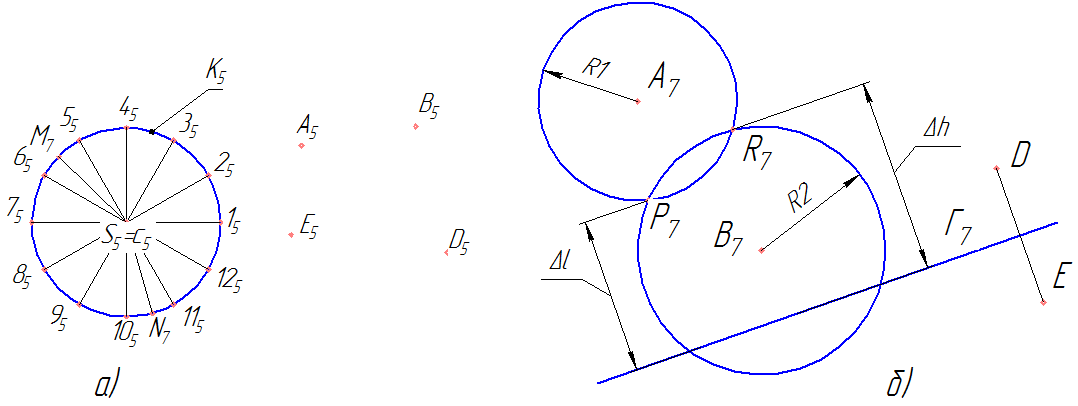
Рис. 1
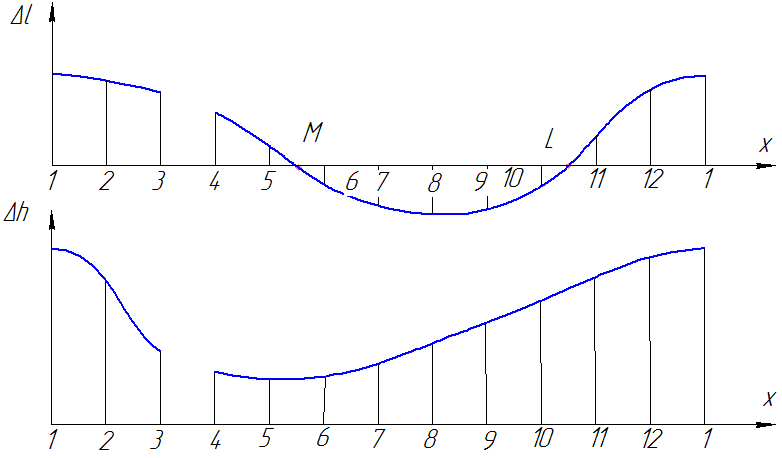
Рис. 2
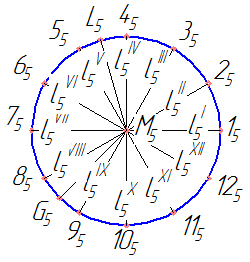
Рис. 3
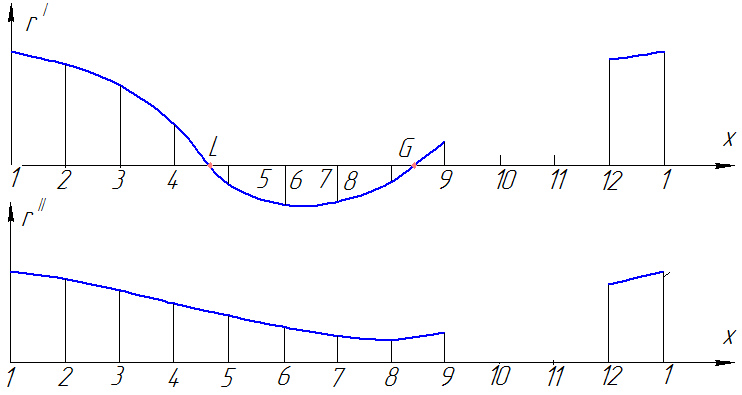
Рис. 4
Вопросы и комментарии к выступлению:

Бойков Алексей Александрович (28 марта 2019 г. 1:02) |
Здравствуйте, Олег Георгиевич! Спасибо за познавательный доклад. Как правидо, в публикациях о методах решения конструктивных задач ограничиваются задачами, не требующими для решения иных инструментов, кроме циркуля и линейки. Вы для решения задачи применяете специальные графики (диаграммы). Построение такого графика предполагается вручную, при помощи сплайна или имеется в виду какая-то автоматизация? Интересно было бы увидеть, возможно или нет решать такие задачи в системе конструктивных аксиом оригами-геометрии (правило Белок позволяет решать уравнения 3-го порядка) или такими инструментами, как пара пересекающиеся коники (в системе конструктивной геометрии Симплекс можно пересеть две кривые второго порядка или при помощи полярного преобразования построить касательные к двум коникам - то есть уравнения 4-го порядка) и др. с уважением, А.Бойков |

Гайдарь Олег Георгиевич (30 марта 2019 г. 12:40) |
Здравствуйте, Алексей Александрович! Спасибо за проявленный интерес. Так называемые «циркульные задачи» были мною тоже рассмотрены ранее, ссылки указаны. Вы правильно обратили внимание на автоматизацию, на предыдущей конференции КГП-17 нами был сделан доклад по постановке задачи – задачи автоматизации решения конструктивных задач, и, как цель, решение их в системах подобных Симплекс. С уважением, О.Гайдарь |
Назад Go Back