ПОСТРОЕНИЕ НЕКОТОРЫХ СЛОЖНЫХ ПОВЕРХНОСТЕЙ КАК ГЕОМЕТРИЧЕСКИХ МЕСТ ТОЧЕК С ПОМОЩЬЮ 3D- МОДЕЛИРОВАНИЯ
English version| Гусева Тамара Викторовна | (Астраханский государственный технический университет) | |

|
Козлова Ирина Алексеевна | (Астраханский государственный технический университет) |

|
Харах Матвей Максимович | (Астраханский государственный технический университет) |
Аннотация
Изучение геометрических мест точек (г.м.т.) рассматривалось в многочисленных работах. В последние годы вновь появились исследования на г.м.т. с учетом новых воззрений. В докладе изучены аналитическим путём г.м.т. двадцати двойных систем, образованных точками, прямыми, плоскостями, сферами, цилиндрами и конусами вращения, расстояния точек которых от заданных систем связаны шестью зависимостями. В докладе рассматривается 3D-модель поверхности 4-го порядка как г.м.т., суммы расстояний которых до прямой и сферы есть величина постоянная, а также 3D-модель поверхности 4-го порядка как г.м.т., отношения расстояний которых до точки и конуса есть величина постоянная.
Ключевые слова: геометрическое место точек, поверхность, аналитическая геометрия, зависимость, 3D-модель
В курсах элементарной, аналитической, начертательной геометриях можно встретить много задач, решение которых связано с нахождением геометрических мест (сокращенно г.м. или множеств), расстояния которых до двух заданных объектов (систем, образов) связаны определенной зависимостью.
Геометрическим местам посвятили свои работы целый ряд авторов [1 ÷ 8, 10, 9 ÷ 12]. Геометрические места точек, лежащие в плоскости и задачи на эти множества подробно описаны академиком Н.Ф. Четверухиным [1]. Простейшие геометрические тела в пространстве рассмотрены Н.В. Наумович [2].
Множествам точек, равноотстоящих от окружностей (в плоскости) или сфер (в пространстве) посвящены работы А.В. Огнева [3].
Много внимания уделено геометрическим местам в работах В.В. Глоговского [4 ÷ 7]. Множество точек, равноудаленных от двух и более геометрических образов им названы эквидистантами двойных и (более) систем по количеству образов, составляющих систему. Им произведено обобщение и систематизирование этого вопроса в направлениях, определяемых: 1) метрикой и размерностью пространства, в котором производится обследование; 2) видом и количеством фигур, по отношению к которым определяется искомое равноотстоящее множество; 3) размерностью элементов пространства, образующих искомое множество. Однако в работах Глоговского В.В., также как и в работах Вышнепольского И.В. [9, 10], появившихся в последние годы, рассматриваются только равноотстоящие множества. Между тем большое количество достаточно интересных геометрических мест можно получить, разыскивая множества, расстояния точек которых от двух данных систем (объектов) связаны какой-то зависимостью.
В данной работе, тема которой предложена д.т.н., профессором Котовым И.И. еще в 1965г., рассматриваются такие множества. Современные методы 3D моделирования позволяют увидеть полученные сложные множества (поверхности) наглядно. В докладе найдены уравнения множеств двадцати двойных систем, образованных точками, прямыми, плоскостями, сферами, цилиндрами и конусами вращения, расстояния точек которых от заданных образов связаны следующими зависимостями:
1. г.м.т., сумма расстояний, которых до двух данных образов есть величина постоянная;
2. г.м.т., разность расстояний, которых до двух данных систем есть величина постоянная;
3. г.м.т., отношение расстояний, которых до двух данных объектов имеет постоянную величину;
4. г.м.т., отношения квадратов расстояний, которых до двух данных объектов имеет постоянную величину;
5. г.м.т., сумма квадратов расстояний, которых до двух данных объектов имеет постоянную величину;
6. г.м.т., разность квадратов расстояний, которых до двух данных образов имеет постоянную величину.
Рассмотрим некоторые из этих множеств.
1. Геометрическое место точек М (x, y, z), сумма расстояний которых до двух данных точек G1 и G2 есть величина постоянная. Точки G1 и G2 заданы следующими координатами для упрощения вычислений G1 (0, 0, g1) и G2 (0, 0, - g1). По формулам аналитической геометрии получим
,
,
.
Величина С должна быть больше расстояния между точками, т.е. С > 2g1. После упрощения получим уравнение множества
,
где ,
,
которое является уравнением поверхности эллипсоида вращения, фокусами которого являются данные точки.
2. Геометрическое место точек M (x, y, z), сумма расстояний которых до прямой G1 и сферы G2 есть Const.
.
После преобразований получим поверхность четвертого порядка
,
где .
В зависимости от расположения прямой и сферы могут встретиться следующие случаи:
а) 2g1 > R - прямая не пересекает сферу;
б) 2g1 = R - прямая касается сферы;
в) 2g1 < R - прямая пересекает сферу;
Сечения полученного множества плоскостями Х = Х1, Х2, ... , Хi дают семейство эллипсов.
Семейство искомой поверхности плоскостями Y = Y1, Y2, ... , Yi и Z = Z1, Z2, ..., Zi дают соответственно семейства кривых четвертого порядка, симметричных относительно оси Z и осей X и Y. С помощью 3D-моделирования выполнена трехмерная модель этой поверхности (Рис. 1).
3. Геометрическое место точек, отношение расстояний которых до точки G1 и конуса G2 есть величина постоянная. Пусть точка G1 задана координатами G1(g1, 0, g2), а конус вращения - уравнением :
По формулам аналитической геометрии находим расстояния от произвольной точки пространства М до данных систем
,
.
Берем отношение этих расстояний
.
Упростив, получим следующее уравнение четвертого порядка
,
где
.
Сечения этой поверхности плоскостями Z = Z1, Z2, ... , Zi дают семейство эллипсов при >
и при
<
, или семейство гипербол при
<
и при
>
, или параболу при
;
а при Zi = 0 получаем прямую линию. Сечения этой поверхности плоскостями Х = Х1, Х2, ... , Хi и Y = Y1, Y2, ..., Yi дают соответственно семейства кривых четвертого порядка. Для случая Х = Х1, Х2, ... , Хi кривые четвертого порядка симметричны относительно оси Z. На Рис. 2 представлена 3D-модель этой поверхности.
Заключение
Итак, получено 120 уравнений г.м.т. Пять уравнений являются уравнениями плоскости, сорок три - поверхности второго порядка, пятьдесят восемь - поверхности четвертого порядка, четырнадцать - поверхности восьмого порядка. Подробное исследование полученных поверхностей, их оптических свойств, на наш взгляд, представляет интерес не только для геометров, но и для специалистов, разрабатывающих отражательные системы в светотехнике, радиоэлектронике и радиолокации.
Список литературы
Рисунки к докладу

Рис. 1 3D-модель поверхности четвертого порядка
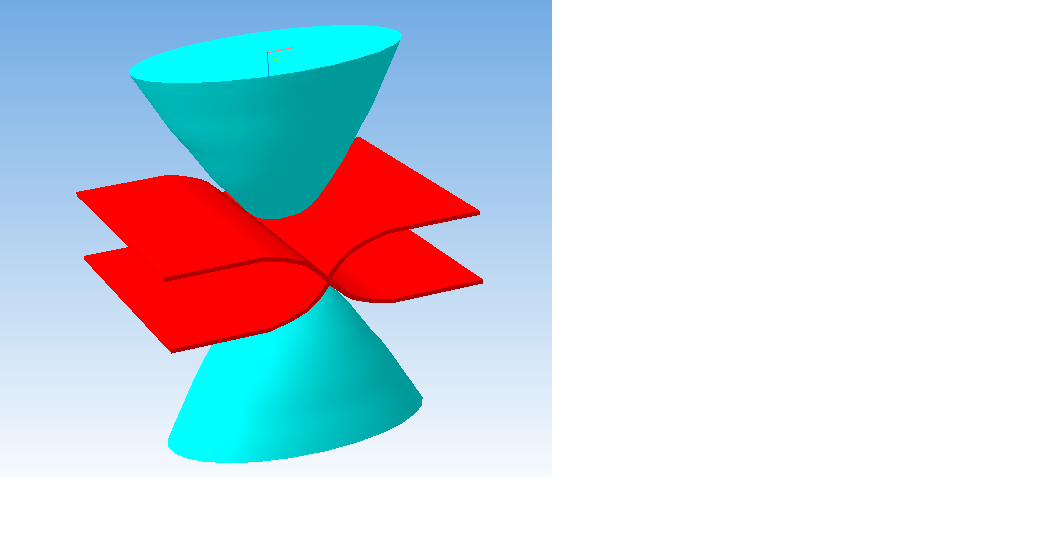
Рис. 2 3D- модель поверхности
Вопросы и комментарии к выступлению:

Хейфец Александр Львович (23 марта 2019 г. 11:32) |
Здравствуйте, коллеги. Несколько вопросов по докладу. Чем вызван выбор шести приведенных Вами множеств из бесконечного множества таких множеств. Что дальше будете делать с полученными 120-ю уравнениями изученных множеств. Было бы интересно увидеть сводную таблицу изученных множеств. Как выполняли 3d визуализацию уравнений. С уважением. А.Л. Хейфец.
|

Харах Матвей Максимович (24 марта 2019 г. 13:18) |
Уважаемый Александр Львович! Как указано в докладе тема данной работы была предложена мне в 1965 году известнейшим учёным д.т.н. профессором Котовым И.И при поступлении в аспирантуру на кафедру прикладной геометрии Московского авиационного института ( ныне технического университета). Мной были найдены 120 уравнений множеств двадцати двойных систем, образованных точками, прямыми,плоскастями, сферами, цилиндрами и конусами вращения, расстояние точек которых от заданных образов связаны шестью зависимостями. Наглядные изображения этих поверхностей строились в аксонометрии методом сечений плоскастями, параллельными координатным плоскостям. Была составлена сводная таблица этих уравнений. Методы 3-D моделирования позволяют ускорить выполнение наглядных моделей этих поверхностей, что видно на рисунке 1 и 2. 3-D визуализация выполнялаь так же методом сечений.Будем благодарны Вам за любые ваши предложения по 3-D визуализации, зная вас как таланливого учёного и крупного специалиста в области 3-D моделирования. С уважением Харах М.М |

Харах Матвей Максимович (24 марта 2019 г. 13:25) |
P.S. Допущена ошибка: читать ПЛОСКОСТЯМИ*! |

Хейфец Александр Львович (24 марта 2019 г. 14:27) |
Матвей Максимович, спасибо за похвалу. "Бальзам на раны". Готов помочь с визуализацией. Но для этого нужен либо построенный объект в AutoCAD'е, и я его визуализирую, либо уравнение. Построю Вашу поверхность и визуализирую. Мой адрес: heifets@yandex.ru С уважением. А.Л. Хейфец. |

Козлова Ирина Алексеевна (25 марта 2019 г. 12:23) |
Уважаемый Александр Львович! Как отметил Матвей Максимович, 3D-модели выполнялись операцией "По сечениям" в САПР КОМПАС-3D. В дальнейшем обратимся также к Вам. |
Назад Go Back