ПОИСК МЕТОДОВ УЛУЧШЕНИЯ ВОСПРИЯТИЯ СТУДЕНТОМ МОДЕЛИ ТРЕХМЕРНОГО ПРОСТРАНСТВА НА ПЛОСКОСТИ В «НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ»
English version

|
Пеганов Михаил Георгиевич | (Московский государственный технический университет им. Н.Э. Баумана) |
Аннотация
В Статье рассмотрены вопросы понимания графического отображения пространственных задач «Начертательной геометрии». Показано, что истолкования чертежа влияют на репрезентацию решений задач. Сказано, что необходимо использовать язык для выражения интеллектуальных действий на чертеже.
Ключевые слова: Начертательная геометрия, функциональный анализ, учебный процесс, аспект, язык
Введение.
В начертательной геометрии есть простая задача: построить проекции точки пересечения прямой и плоскости общего положения. Такая задача входит как составная часть (фрагмент) в алгоритм решения широкого круга задач: позиционных и метрических, в частности как фрагмент, она входит в домашнее задание. Некоторая часть студентов находила решение задачи вовсе не тем методом, который давался на занятиях, а суждения студентов о построениях не совпадали с отображениями решений на чертежах. У преподавателя возникал когнитивный диссонанс, побуждающий искать причины и выходы из него.
В данной работе предлагается попытка поиска причин появления в решениях задач различий между преподаваемыми и применяемыми, попытка внесения корректив в образовательный процесс в связи с выявляемыми причинами.
Функциональный анализ возникновения двух методик решения.
В процедуре образовательного процесса важным элементом учебной работы является оценке качества обучения. В стандарте качества ГОСТ Р 52614.2-2006 «Руководящие указания по применению ГОСТ Р ИСО 9001-2001 в сфере образования» [1] отмечено, что «Контроль качества – основополагающий процесс в системе менеджмента качества. При оценке работы людей сложно провести точное измерение. Оценку обычно проводят во время образовательного процесса». Так же стандарт направлен на применение «процессного подхода» к функционированию системы образования.
В данной работе использовалась системная модель образовательного процесса [2 стр. 68], в которой можно выделить границы функций и связность их отношений. Были определены функции и этапы обучения, В которых появлялись работы студентов с двумя различными методиками выполнения домашних заданий.
В учебный процесс входит процедура «Выполнить контролируемые работы этапа». В этой процедуре регулярно обнаруживались решения упомянутой выше задачи по начертательной геометрии методом, отличающимся от того, который рекомендован на обычных плановых занятиях.
Причины появления различных решений можно трактовать так:
студенты, активно работавшие на учебных занятиях в аудитории, посещавшие консультационные занятия, на которых рассматривались методы решения домашних заданий, вместе с действующими картинами решений задач получали словесную поддержку со стороны преподавателей - «фиксация образов состоит в словесном описании их – преподаватель должен объяснять сущность и обобщать действия» [2 стр. 68]. На занятиях предлагалось выполнять решение задачи построения проекций точки пересечения прямой и плоскости общего положения с применение методики, изложенной в работе [3 стр. 95];
студенты, которые были замечены, как не посещавшие консультационные занятия, предъявляли выполненные решения задач, содержавшие построения проекций точки пересечения прямой и плоскости общего положения, по иной методике. Построения легко признавались ошибочными, но лишь потому, что студенты не могли правильно объяснить и защитить выполненные построения – им явно не хватало объёмного представления чертежей, понимания конфигурации размещения объектов, не хватало слов для объяснения сущности своих действий.
При исследовании работ и слушании объяснений студентов по поводу решений задач, я сам наталкивался на мысль: «Всё проводимое языком упорядочение только условная игра, заведомо ничего не упорядочивающая и как бы напоказ подчеркивающая свой условный характер, словно нарочно для того, чтобы никто не принял это за настоящее упорядочение, после которого не понадобилось бы другого, реального» [4 стр.191]. Наблюдалась ситуация несоответствия смыслов словесных объяснений с реально выполненными построениями на чертеже. У студентов терялись понимание объемности чертежей, доказательность построений.
Анализ на основе методологии Людвига Витгенштейна.
Анализ касался решения задачи по методике отличающейся от преподаваемой на занятиях. Использовались материалы работы Людвига Витгенштейна «Философские исследования» [5]. Книга имеет педагогическое направление – изложена как диалог людей, один из которых учитель. В диалогах рассматривалось языковая деятельность, работа с образами и восприятием изображений на чертеже. Хоть работа с книгой не дает ответ, каким должен быт язык, но она позволяет понять и приблизить к систематизации некоторые возможности управления образовательным процессом.
Если не вступать в диалог со студентом во время просмотра чертежа выполненной им работы, то решение задачи построения точки пересечения прямой общего положения и плоскости общего положения можно было бы признать как выполненным. Но вступление в речевой диалог со студентом (это обязательный атрибут проверки выполнения домашнего задания) вызывало несоответствие чертежных построений со словами (суждениями) студентов.
Все элементы на чертеже на всех шагах решения сохраняли свое бытие (свои связи друг с другом) – они были неподвижны. Слова студентов демонстрировали вольную смену связей элементов и описывали элементы чертежа как вольно живущих субъектов - их связи друг с другом менялись исходя из удобств прохода к цели. Это недоразумение трубовалось исследовать, но не как функции и структуры языка, а сущности (смыслы) языка, которые мы видим и слышим вслушиваясь в тексты. В работе [5 стр. 75, стр. 265] ясно показано, что наше сознание наделяет предложения и слова смыслом, а для общения с другими людьми тексты должны обладать общим ясным обликом. Студент в своей работе первым шагом выполнял операцию: Истолкование изображения и определение проекций точек 1' и 2' - истолковывал чертеж и видел так, как истолковывал – это значит, что получал зрительный опыт посредством истолкования, т.е. создавал косвенное описание, этот феномен назван «Заметить аспект» [5 стр. 281]. Аспект (атрибут чертежа) - это категория, которая выражает различие между начальным видом чертежа и следующим [5 стр. 280].
В процессе всего времени решения на чертеже не изменяется конфигурация положения элементов. От студента требуется определить конфигурацию точек на чертеже, руководствуясь только рассуждениями. Наверное, студент знает, что нужны точки 1' и 2', которые следует найти на линии d', но не видит объемности в изображении линий b, c и d (этот факт подтверждается в процессе проверки выполнения домашнего задания: на вопрос: «что значат точки 1' и 2' на горизонтальной плоскости проекции», студент достаточно уверенно отвечал: «точки 1'и 2' - точки пересечения линии d с исходной плоскостью b ∩ c = A»).
Второй шаг: Построение проекций точек 1'' и 2''. Теперь студент проецирует точки на фронтальную плоскость проекции и толкует проекции точек: принадлежат линиям b и c. Суть в том, что аспект изменился – на предыдущем шаге были определены проекции точек 1 и 2 как принадлежащие линии d, а на текущем шаге проекции тех же точек на фронтальной плоскости проекций стали принадлежать линиям b и c. Хоть произошло «изменение аспекта» на глазах студента – это можно назвать как новое восприятие, но для студента восприятие осталось прежним – он «усвоил аспект» [2 стр. 284] (приобретенное знание, как воля, действует на видимою картину). «Глядя на предмет, не обязательно думаешь о нем» [2 стр. 286], т.е. глядеть не значит видеть. В итоге, в суждениях студента получается: сообщение не об увиденном, а представление «увиденного» - «усвоенного аспекта». Студент не видит объёмно, но порой думает, что видит. Нужна особая практика и тренировка для объемного представления на рисунке или в словах [5 стр. 288].
На линиях b" и c" появляются точки 1''и 2'', через эти точки проводится линия (1''-2'') - проекция линии b на фронтальную проекцию плоскости b ∩ c = A). В пересечении линии (1''-2'') с линией d'' строится точка K" - проекция точки пересечения линии d с плоскостью b ∩ c = A».
Третий шаг: Определение положения проекций точек пересечения линии d и исходной плоскость b ∩ c = A. Размещение на горизонтальной плоскости проекций на линии d' точки K' - второй проекции точки пересечения прямой и плоскости общего положения - K. Задача решена правильно.
На рис.1 пошаговый ход выполнения задачи приведен в виде Структуры поиска решения задачи. Структура выполнена по правилам, изложенным в разделе «Системное представление» работы [2 стр. 68].
На схеме структуры приведены три процедуры-функции:
1 Истолкование чертежа и внесение изменений (познание) – в работе [5 стр. 310] сказано: «Истолковывать значит мыслить, что-то делать», но почему проявляется слепота к объемности видимого? Как показал пример ответа студента на вопрос о точках (1' и 2' – как вы их получили?) – «речь» и «мышление» не состоят в связи. При истолковании работает воображение. «Видеть аспект и воображать – проявление воли. Возможен приказ “Вообрази это”, а также: “Теперь смотри на фигуру так”; но не: “Теперь этот лист зелёный”» [5 стр. 311], т.е. здесь в обучении нужно использовать не описание, а приказ. Нужен преподаватель, который внешним воздействием – речью, приказом преодолеет возникшее внутри студента сопротивление пониманию.
2 Репрезентация чертежа (демонстрация знания чертежа) – Эта функция должна служить для подготовки речевого сопровождения всех решений.
При решении данной задачи отображение ее на чертеже остается неизменяемым: все линии, все точки всегда остаются на месте.
Если мы не в состоянии выделить конкретное телесное действие, которое указало бы на элемент, мы говорим об интеллектуальном действии. Это действие описывает наш язык - появляется картина (отоброжение) [5 стр. 269].
3 Проверить домашние задания и анализировать выполнение работ – эта функция исполняется преподавателем. Она должна быть встроена в процедуру «Выполнить контроль и анализ качества знаний и успеваемости» в системе образовательного процесса описанной в работе [2 стр. 68].
Сущность процесса решения, озвученная студентом, выражается в словах и суждениях. В диалоге необходимо задать вопрос студенту в третьем лице: «Осознается ли в отображении пространственный характер, глубина положения элементов, чувствуется ли это все время?», если спросить его самого, это будет его смущать [5 стр. 308].
|
|
|
Рис. 1 Проект функциональной схемы выполнения решения задачи о пересечении прямой и плоскости общего положения. |
В рамках системного представления образовательного процесса в техническом университете, приведенном в [2 стр. 68], после выполнения процесса «Выполнить контроль и анализ качества знаний и успеваемости» преподаватель может вынести суждение о качестве усвоения изучаемого материала и оформить коррекцию обучения. «Преподаватель возвращается к процедуре “выполнить этап образовательной деятельности” с результатами анализа проведенного этапного контроля работ студента…, представляя студента как объект обучения, может определить траекторию движения этого объекта в среде технического университета» [2 стр. 68].
Выводы.
Для выполнения задачи построения проекции точки пересечения прямой и плоскости общего положения может быть использован метод, описанный в данной статье. От исполнителя требуется умение объяснять свои построения на чертеже.
В образовательном процессе есть
- студенты, активно работающие на учебных занятиях в аудитории, посещающие консультационные занятия – работающие с преподавателем;
- студенты не посещающие консультационные занятия – работающие без преподавателя. Самостоятельная интерпретация может нарушить восприятие модели трехмерного пространства на плоскости.
Суть в том, что преподаватель и студент являются совокупным субъектом всего образовательного процесса[2 стр. 68]. Студент должен работать с преподавателем, который внешним воздействием – речью, приказом, преодолеет возникшее внутри студента сопротивление пониманию.
Студент должен учиться использовать язык для выражения своих интеллектуальных действий на чертеже. Интеллектуальные действия определят контекст употребляемых в общении слов, – тогда язык обеспечит интеллектуальную коммуникацию.
Использование следящей системы управления и коррекции обучения в системе образовательного процесса [2 стр. 68] позволяет оперативно внести коррекции в процесс изучения «Начертательной геометрии» в течении семестра.
Список литературы
Рисунки к докладу
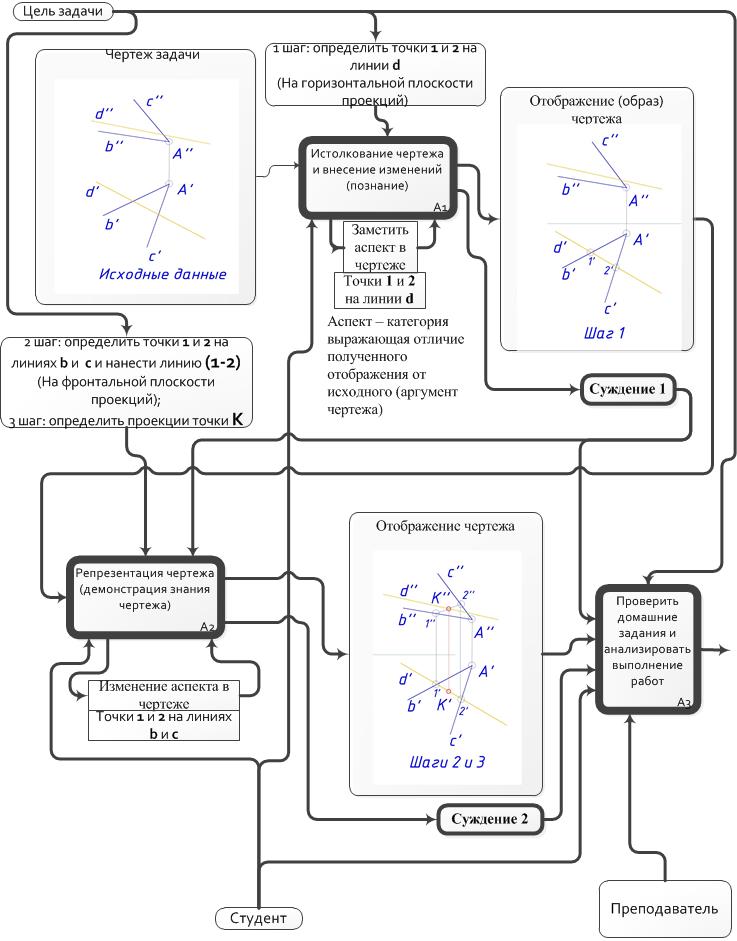
Рис. 1 Проект функциональной схемы выполнения решения задачи о пересечении прямой и плоскости общего положения.
Вопросы и комментарии к выступлению:

Горнов Александр Олегович (22 марта 2019 г. 13:24) |
Михаил Георгиевич, здравствуйте ! Извините , но все это выглядит как - то очень "тяжеловесно". Проблема -то чисто внутренняя для методов начертательной геометрии, обладающих невысокой наглядностью. Сомневаюсь , что, если студент даже и освоит сиё, то где нибудь использует, кроме как внутри самой дисциплины в рамках одной -двух задач . С уважением, А,О, |

Пеганов Михаил Георгиевич (23 марта 2019 г. 2:29) |
Здравствуйте, Александр Олегович. Я согласен, в начертательной геометрии любое решение выглядит тяжеловесно. Но Студент самостоятельно не видит объемности рисунка, лишь имеет в поле зрения сразу все точки на одной плоскости.А потом, если студент, не различающий объема на чертеже, станет инженером, спроектирует робота и попытается написать программу поиска точки в пространстве или просто ориентирования в пространстве, в котором надо что-то найти или пробиться к какой-то точке, как этот инженер опишет решение? Задачи ориентации в пространстве мы сами решаем на каждом шагу. |

Горнов Александр Олегович (23 марта 2019 г. 9:40) |
Да, Михаил Георгиевич, картина предстает мрачная ... Но. что и я часто подчеркиваю. - задачи ориентации в пространстве мы сами решаем на каждом шагу- и не только мы, но и студенты. Что касается пространственных роботов, то их движение задается , как правило автопрограммированием . Рабочий орган перемещают в пространстве по желаемой траектории, а микропроцессорная система управлением запоминает координаты движения, а потом воспроизводит необходимое число раз . ... А что будет делать студент, освоивший алгоритм описанной задачи, если я задам плоскость точкой и прямой ? Я к тому, что сначала надо опираться на естественные навыки студента ориентироваться в пространстве. сначала предлагая ему для анализа более легко воспринимаемые модели пространства , а затем более сложные , когда он должет его реконструировать попарно оперирую его координатами . Это и будет часто упоминаемое здесь: от простого к сложному. А еще естественней: попутно и от целого к части, что соответствует ненавязанной логике познания. C уважением, успехов, А.О.
|

Дударь Елена Сергеевна (24 марта 2019 г. 13:57) |
Добрый день, Михаил Георгиевич! Спасибо, за интересный доклад. Увидела в Вашей публикации то, что часто является предметом обсуждения с коллегами , а именно попытку понять проблемы восприятия нового знания конкретным индивидуумом. Полагаю, что под таким индивидуумом мы с Вами понимает среднестатистического студента, которому по каким-то объективным причинам (когнитивным в том числе) трудно дается понимание нового. Вы очень точно подмечаете, как впрочем и многие другие участники этой конференции, что у современных студентов "речь и мышление не состоят в связи". Есть ли в Вашей педагогической практике эффективные приемы "пробуждения" связи вербальной информации и мышления для конкретного индивидуума, а также налаживания интеллектуальной коммуникации "преподаватель-студент"? С уважением, Елена С. Дударь
|

Пеганов Михаил Георгиевич (24 марта 2019 г. 18:33) |
Добрый день, Елена Сергеевна. Спасибо за проявленный интерес к моей работе. Само исследование педагогической эффективности «пробуждения связи информации и мышления» пока что не опробовано. Только намечается проверить выводы работы: - выявить действительный эффект различия посещаемости и непосещаемости консультаций по выполнению домашних заданий; -- проверить эффективность приказного, резкого тона для преодоления у студента воли, удерживающей его отображения (здесь могу сказать, что приходилось преодолевать коллективную волю группы методом перехода на резкие тона на занятиях, т.е. переходил к жесткому соблюдению правил, когда группа пыталась проявить так называемый «пофигизм» к начертательной геометрии); - применить обращение (по поводу ошибок) к студенту в третьем лице проработать методику такого обращения, чтобы получилось обсуждение ошибки какого-то третьего лица и это не затрагивало бы самолюбие студента; - обязательно включить в требование к отчету о выполнении домашней работы "суждение" – речь, ясно выраженную словами. С уважение, Михаил Георгиевич Пеганов |
Назад Go Back