ЛЕНТОЧНЫЕ РАЗВЕРТКИ ТОРА

(Московский государственный технический университет им. Н.Э. Баумана)

Соавтор(ы): Христофоров Павел Андреевич, Петрова Ольга Владимировна

Аннотация

Статья посвящена построению различных видов разверток торовой поверхности методами начертательной геометрии. При этом решена задача построения условной развертки тора без разбиения ее на отсеки. В работе продемонстрирована возможность формообразования сложных поверхностей из плоских разверток.

Ключевые слова: Начертательная геометрия, развертка, тор, торсовая поверхность

Введение

В последние десятилетия в мировом машиностроении широко используются полимерные композиционные материалы (ПКМ) на основе стекло-, угле- , боропластиков и т.п. Композитные материалы нашли широкое применение в производстве аэрокосмической техники, автомобилей, бытовых товаров.

В свою очередь появление новых материалов с особыми свойствами потребовало разработки новых технологий изготовления деталей и сборочных единиц. В общем случае технология изготовления деталей из полимерных композиционных материалов включает в себя следующие основные операции: подготовку армирующего наполнителя и приготовление связующего; совмещение арматуры с матрицей; формообразование детали; отверждение связующего в композитных материалах; механическую доработку детали; контроль качества. В качестве армирующего наполнителя используются нити, жгуты, ленты и ткани. Основными технологическими процессами формообразования изделий из ПКМ являются: контактное формование, формование с эластичной диафрагмой, намотка и ряд других процессов [1].

При формообразовании сложных поверхностей вышеуказанными методами при применении лент и тканевых элементов армирующий материал укладывается на оправку или с гарантированным зазором между соседними элементами, или внахлестку. Это в свою очередь ведет к образованию пор, уменьшению прочности и т.д.

В данной работе рассматривается задача определения формы армирующего материала для формообразования деталей с торовой поверхностью с возможностью укладки с минимальными зазорами, то есть задача создания условной развертки тора из одного элемента. Условной – поскольку тор относится к неразвертываемым поверхностям.

В курсе начертательной геометрии дается метод построения условных разверток неразвертываемых поверхностей [2].

На первом этапе неразвертываемая поверхность разбивается на ряд участков. Каждый из этих участков заменяется участком криволинейной развертываемой поверхности (конус, цилиндр). На втором этапе каждый участок развертываемой поверхности аппроксимируется соответствующей ей многогранной поверхностью. После этого получают развертку многогранной поверхности, которая и будет называться условной разверткой неразвертываемой поверхности.

В случае построения типовой развертки торовой поверхности, участок, “вырезанный” двумя плоскостями, проходящих через ось тора, заменяется на участок цилиндрической поверхности (рис.1). На втором этапе цилиндрическая поверхность преобразуется в призму, развертка которой и будет являться условной разверткой участка торовой поверхности.

Для построения условной развертки тора без разбиения на участки, необходимо заменить всю поверхность тора на некоторую торсовую, вписанную в тор или описывающую его. В качестве направляющей линии такой поверхности удобно выбрать линию торового соленоида, а образующие линии располагать в плоскостях или проходящих через ось тора или перпендикулярных ей.

При анализе результатов построения линии торового соленоида выяснилось, что строить торсовую поверхность между соседними витками соленоида удобно, если n > 10-15. Коэффициент “n” определяет количество витков соленоида в случае, если “n” целое число. На рис.2 показано расположение направляющей и образующих линий торсовой поверхности при n=36. В зависимости от размеров тора и числа n длина развертки может достигать нескольких десятков метров.

Построение самой развертки основано на применении способа триангуляции.

При 1<= n <=10 линия соленоида имеет такую форму, что использовать ее как направляющую торсовой поверхности не представляется возможным, поскольку такая поверхность будет крайне далека от формы тора (рис. 3 а.). Однако, если указанную линию повернуть вокруг оси тора на небольшой заданный угол, то между основной и повернутой линиями можно построить торсовую поверхность, соединив их образующими линиями, лежащих в плоскостях перпендикулярных оси тора (рис. 3 б.). Последним этапом будет построение элемента развертки и определение количества таких элементов для полного перекрытия торовой поверхности (рис.3 в.).

При 0< n <1 каждый виток линии соленоида располагаются вокруг оси тора, а образующие торсовой поверхности, соединяющие соседние витки соленоида, построены в плоскостях, проходящих через ось тора.

После выполнения алгоритма построения условной развертки была определена ее форма, показанная на рис.4 а., элементы развертки распечатаны на бумаге с сохранением цвета и склеены в единую ленту. После этого была произведена склейка модели тора (рис.4 б). Как и при склейке сферы [3] витки развертки тора соединялись только с соседними витками (это легко проследить по цвету витка) без использования каркаса или внутреннего наполнителя.

Результаты работы применяются автором при чтении лекций по курсу «Начертательная геометрия» в разделе «Развертки поверхностей».

Выводы:

Научная (геометрическая) составляющая поставленной задачи авторами выполнена в полном объёме. В качестве первого шага в подготовке производственного эксперимента авторы обратились к руководству кафедры «Ракетно-космические композитные конструкции» о введении данной тематики в список выпускных работ бакалавров.

Список литературы

Буланов И.М., Воробей В.В. Технология ракетных и аэрокосмических конструкций из композиционных материалов: Учеб. для вузов. М.: Изд-во МГТУ им. Н.Э.Баумана, 1998 - 516 с., ил.
Жирных Б.Г., Серёгин В.И., Шарикян Ю.Э. Начертательная геометрия: учебник. / Под общ. ред. В.И. Серегина – 1-е изд. – М. : Изд-во МГТУ им. Н.Э. Баумана, 2015. – 176 с.: ил.
Федоренко В.И., Кучеров К.В., Христофоров П.А. Лента Федоренко – условная развертка сферы // Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации. 2017. Т. 1. С. 379-384.

Рисунки к докладу

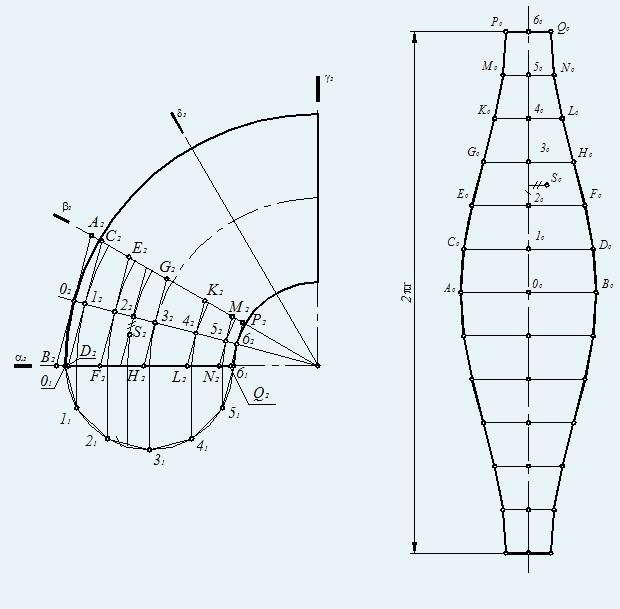
Рис. 1 Типовой вариант создания развертки тора по участкам

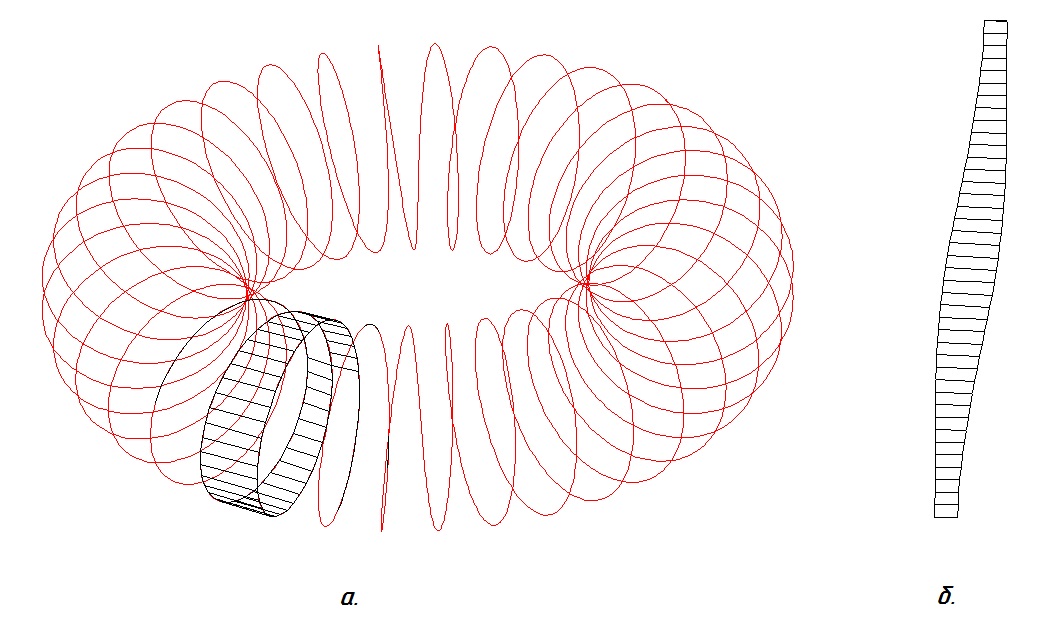
Рис. 2 а) направляющая линия (торовый соленоид при n=36) с элементом апроксимирующей поверхности; б) элемент развертки

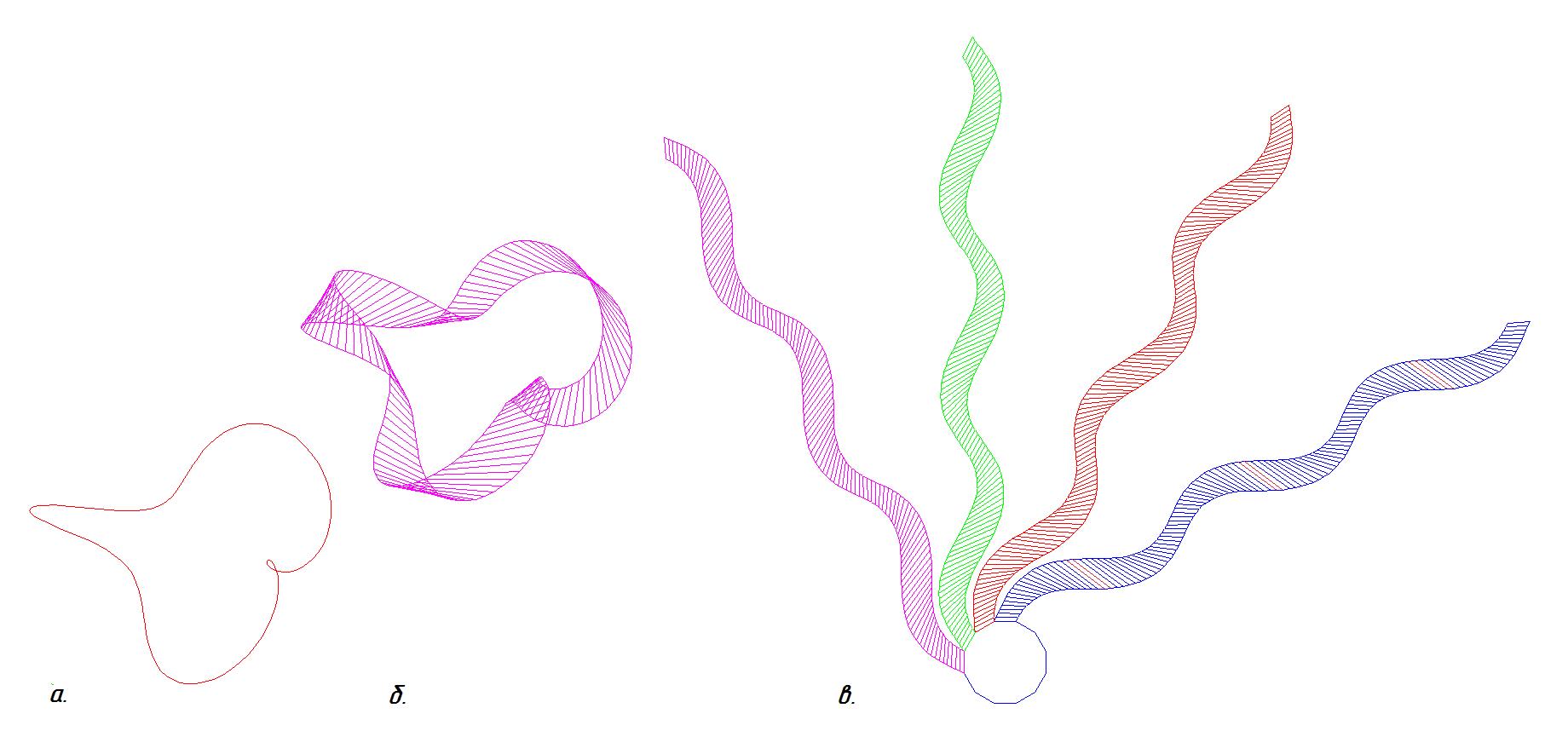
Рис. 3 а) Направляющая линия - торовый соленоид при n=3; б) Участок апроксимирующей поверхности тора; в) Развертка торовой поверхности

Рис. 4 а) Развертка торовой поверхности с направляющей линией в виде торового соленоида при n=0,1; б) Модель торовой поверхности

Вопросы и комментарии к выступлению:

Хейфец Александр Львович
(25 марта 2019 г. 21:28)

Коллеги, очень интересный доклад.

Я применяю нить, намотанную на тор (трилистник) в качестве направляющей поверхности Эшера. Эта типовая студенческая работа по спецкурсу. Но там всего лишь три витка за два оборота и все можно сделать вручную. Для Вашего примера, конечно, нужно программирование. Вопрос: как Вы программировали? В каком пакете строили?

В качестве подарка высылаю студенческую работу на близкую тему, выполненную в AutoCAD с доработкой в PhotoShop. Если интересуют подробности - см. А.Л. Хейфец. Инженерная компьютерная графика. Опыт преподавания и широта взгляда. М:, 2002 г.

С уважением. А.Л. Хейфец