1.1.3.
деление окружности на равные части
В основе построения правильных
различных многоугольников лежит деление описанной вокруг них окружности на
равные части.
Деление
окружности на три, шесть и двенадцать частей
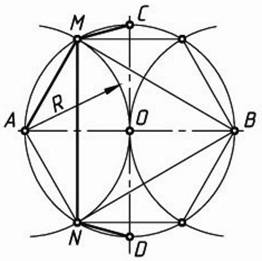
В окружности заданного радиуса R проводят через центр О взаимно перпендикулярные оси АВ
и CD. Из любой части конца диаметра (например, А) проводят радиусом R дугу до пересечения с окружностью в точках М и N.
Отрезок MN –
искомая сторона правильного вписанного треугольника MВN.
В свою очередь, отрезки АM=АN и СM=DN соответственно равны сторонам правильных
вписанных шестиугольника и двенадцатиугольника.
Деление
окружности на пять и десять частей
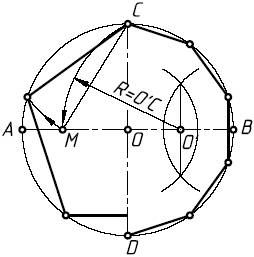
Проводят два взаимно перпендикулярных
диаметра АВ и CD и делят радиус ОВ
пополам в точке О'. Из точки О', как из центра, проводят дугу
радиусом О'С до пересечения ее с
диаметром АВ в точке М.
Отрезок СМ равен стороне правильного вписанного пятиугольника, отрезок ОМ – стороне десятиугольника.