|
|
Бойков Алексей Александрович | (Ивановский Государственный Энегретический Университет им. В.И.Ленина) |
В статье рассматриваются некоторые аспекты, связанные с алгоритмизацией курса начертательной геометрии.
Введение
Авторы доклада [1] обозначили ряд проблем, возникающих в случае преподавания начертательной геометрии (НГ) на основе принципов алгоритмизации. Сходные выводы можно проследить в работе [2], где отмечается, что преподавание НГ на формально-логической основе создает опасность того, что образное мышление студентов остается неразвитым. Различные аспекты алгоритмизации и формализации начертательной геометрии неоднократно рассматривались ([3-9] и др.). Алгоритмы использовались при изложении материла в учебных пособиях [10-13], которые нам трудно в чем-либо упрекнуть. Кроме того, решение конструктивных задач всегда осуществляется по тому или иному алгоритму ([14-19], статьи в выпусках сборника «Прикладная геометрия и инженерная графика» и др.). В связи с чем представляется необходимым рассмотреть подробнее и вскрыть причины противоречий, приводящих к появлению указанных проблем.
1.
Алгоритмом называется точно определенное правило действий (курсив наш), для которого указано как и в какой последовательность его необходимо применить к исходным данным задачи, чтобы получить ее решение (Четверухин Н. Ф. Теоретические основания начертательной геометрии. М.: МАИ, 1978).
Первоначально алгоритмами назывались сочинения по искусству счета, в частности, известен алгоритм Евклида для вычисления наибольшего общего делителя, приведенный в «Началах» отдельно для целых чисел и отрезков. В начале XX века алгоритмы обрели статус «базисного» понятия математики. С появлением и распространением вычислительной техники — главным инструментом решения прикладных задач любого рода. В этой области — области разработки программ для ЭВМ — алгоритмы, в образе программ и языков программирования, неоднократно видоизменялись и привели к появлению ряда подходов к описанию способов решения задач (концепций языков программирования) [20]:
Инженерная геометрия в полной мере использует возможности новых подходов к программированию. Так, форматы файлов CAD-систем реализуют предметно-ориентированный подход, так как являются современными «потомками» дисплейных файлов [21, 22] — «программ графического процессора», создание которых (программирование) осуществляется в результате геометрических построений и команд. Наоборот, в геометро-графическом образовании, например, в [23], геометрические и графические алгоритмы рассматриваются в своей самой начальной, линейной форме.
Примером системы, дающей возможность говорить о графических алгоритмах на новом современном уровне является, например, «Симплекс» ([24, 25] и др.).
Таким образом, мы можем сделать предварительный вывод: то, что традиционно понимается под алгоритмизацией НГ, не использует и половины возможностей действительной алгоритмизации, застыв на уровне 70-х гг.
2.
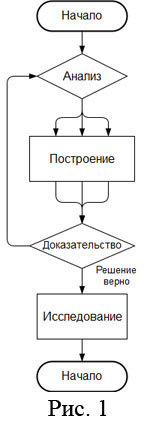О тветим теперь на вопрос, так ли плохи простые алгоритмы, как отмечается в [1]. На рис. 1 приведен базовый алгоритм решения конструктивной задачи [14, 26, 27]. Если студент будет им пользоваться при решении, должен ли снизиться его уровень геометрического образования? умение решать задачи? Очевидно, нет. В различных областях промышленности и деятельности человек постоянно имеет дело с разного рода инструкциями, типовыми методиками и пр., которые являются алгоритмами решения типовых задач. Плохо ли это? Действительно, любая инструкция, типовая методика и готовый алгоритм «укладывают на прокрустово ложе» многообразие способов получить результат. Следует ли от этого отказаться? Отменить ГОСТы и дать возможность каждому студенту изобретать новую знаковую систему?
Кроме несомненных недостатков, любая стандартизация имеет и неоспоримое достоинство — освобождает творческие ресурсы для решения нетиповых задач за счет механизации типовых. Типовые алгоритмы НГ должны освободить творческие ресурсы и время студентов для решения курсовых и научно-исследовательских задач. Если этого не происходит, следует разобраться в причинах, но алгоритмы как таковые здесь не при чем.
3.
Алгоритмизация НГ имеет две принципиальные проблемы.
3.1. Первая связана с двойственностью самих алгоритмов. Действительно, большинство алгоритмов традиционного курса НГ — алгоритмы стереометрии с участием точек, линий и тел обыкновенного евклидова пространства. Но эти алгоритмы реализуются при помощи построений на плоскости. Здесь уместным будет термин интерпретация, использованный В. Ф. Каганом в [28]. Традиционная НГ является интерпретацией евклидовой геометрии, в которой (возьмем для определенности двухкартинный чертеж в системе фронтальной и горизонтальной плоскостей проекций) «точкой» называется пара точек плоскости, «проецирующей прямой» — одна точка и проходящая через нее вертикальная прямая, «прямой» — пара прямых, — соответствующим образом размещенных и обозначенных. В некотором смысле начертательная геометрия — первый для студентов опыт знакомства с интерпретацией формальной математической модели (им еще предстоят другие модели — тепловых и химических процессов, движения объектов, и др) и опыт знакомства с интерпретацией геометрии.
Возможны и другие интерпретации [29]: примем считать «точкой» точку плоскости с числовым индексом — получим проекции с числовыми отметками, примем считать «точкой» окружность некоторого радиуса — получим циклографический чертеж [30].
Это предполагает, что каждый элемент задачи должен всякий раз заново кодироваться. Поэтому наравне с алгоритмами решения задач возникают типовые процедуры кодирования. Проблемой является то, что в некоторых учебниках «алгоритмы» решения задач составляются как смесь первых и вторых, что не допустимо, да и, в общем-то, не нужно.
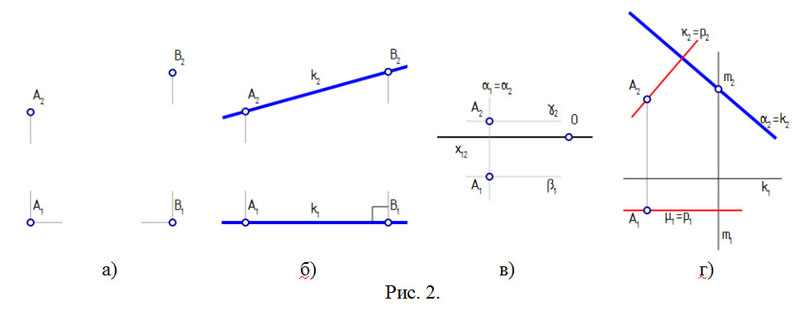
Рассмотрим пример 1. Пусть требуется через данные точки A и B провести прямую k (рис. 2, а-б). Этап анализа (рис. 1) проводится в следующем порядке [9]: анализируются свойства объектов чертежа, выявляются свойства задаваемых ими объектов пространства, формируется пространственный алгоритм и его интерпретация. Для наглядности на первых этапах всю соответствующую информацию можно сводить в таблицу (таблица 1).
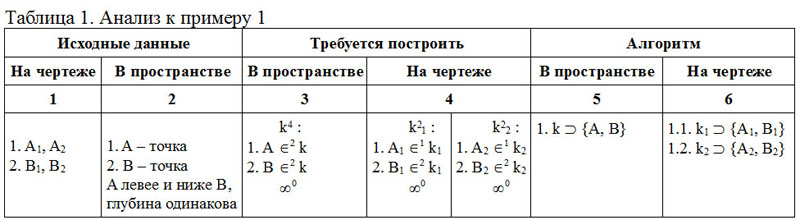
Заполнение таблицы осуществляется как последовательность ответов на вопросы:
Шаги 1-2 — чтение чертежа.
Шаги 3-4 — формирование модели задачи. Одновременно с этим может быть выполнен параметрический анализ условий (число параметров объектов и условий показано верхними индексами) и выполнена оценка ее определенности. С точки зрения декларативной концепции программирования такая модель задачи уже достаточна для ее машинного решения и может считаться программой для соответствующего вычислителя.
Шаги 5-6 — синтез императивного алгоритма решения, то есть последовательности построений. Содержимое колонки (3) является неявной формой алгоритма (5), колонки (4) — неявной формой алгоритма (6).
Колонки 2, 3 и 5 отвечают за пространственное содержание задачи, 1, 4 и 6 — за интерпретацию пространственного содержания выбранным способом. Пространственное содержание задачи инвариантно относительно ее условий.
На этапе построения (рис. 1) должны быть практически реализованы операции, перечисленные в колонке 6.
На этапе доказательства (рис. 1) требуется показать, что полученная комбинация фигур на чертеже действительно является решением задачи. Для этого тоже используется таблица, поскольку в колонке 3 записаны все условия, выполнение которых необходимо и достаточно для того, чтобы полученное решение было правильным, а в колонке 4 — условия того, что интерпретация соответствует этому решению.
Когда способы представления объектов и условий задачи становятся привычны, колонки 1, 4 и 6, в принципе, оказываются не нужны, но в самом начале обучения они необходимы.
Таким образом, правильная алгоритмизация обладает множеством достоинств, однако не всегда анализ и составление алгоритма могут быть выполнены так же безоговорочно и ясно. Рассмотрим пример 2. Пусть требуется построить чертеж точки, заданной координатами, — A (50, 25, 10).
И анализ, и алгоритм решения далеко не так изящны, как в примере 1. Что непосредственно подводит нас ко второй проблеме.
3.2. Вторая проблема НГ, присущая конструктивной геометрии, в целом, связана с отсутствием подходящего языка для выражения построений. Пример 2 показывает, что далеко не все геометрические условия, появляющиеся в задачах, могут быть легко записаны. Как, к примеру, указать, что линия связи вертикальна, а ось «x12» — горизонтальна; что «A1» левее «O» на 50?
Еще хуже обстоит дело с построениями. Как отложить 50 влево? Как построить окружность m с центром в точке A радиусом 25? Как различить прямую m и окружность m? Как отличить проекцию l1 в виде точки от проекции l1 в виде прямой?
В научных трудах эта проблема решается приведением чертежа решения, где объекты представлены наглядно. В учебном процессе, когда задача еще не решена, и решение еще невозможно увидеть, нет ничего, на что можно было бы опереться, кроме геометрических свойств фигур и связывающих фигуры условий, которые, как было показано, не имеют подходящей формы выражения.
В целом, когда задача проста, можно использовать словесное описание, как в примере 2. Можно даже смириться с тем, что символические формулы неминуемо смешиваются со словесными, и в одном алгоритме могут встретиться «построить», «провести», «соединить», «начертить» и др. Все это неминуемо создает путаницу, но даже не это является сутью проблемы.
Рассмотрим пример 3. Пусть требуется определить расстояние между точками A (50, 25, 10) и B (5, 0, 35). Пример 2 показал, как формируется алгоритм построения чертежа точки A, но чертеж точки B строится аналогично. Ни словесная, ни символическая запись не предоставляют однозначного, не громоздкого и не требующего оговорок способа сделать такую ссылку.
Введем словесный алгоритм построения чертежа точки по ее координатам, назовем его ЧТ (x0, y0, z0):
Здесь понятия «отложим на» и «проведем вертикальную линию», «горизонтальная проекция», «фронтальная проекция» и ряд других являются неопределяемыми. Теперь построение точек A и B может быть записано так:
Словесные алгоритмы, наподобие рассмотренного, требуют некоторого числа повторений для того, чтобы возникла ассоциативная связь между понятием чертеж точки, символом и соответствующими действиями. В качестве примера необходимости такой механизации можно привести синусы и косинусы тригонометрии. За каждым из этих понятий стоит свое определение, но при упрощении выражения вроде sin4α + cos4α или sin4105∘⋅cos475∘ задумываться о том, что синус есть отношение противолежащего катета к гипотенузе в прямоугольном треугольнике, — излишне и даже вредно.
С учетом введенных обозначений таблица к примеру 3 примет вид:
Где НВ — словесное описание алгоритма определения натуральной величины. Мнемокоды ЧТ, НВ и др. могут использоваться и для более свободной формы описания алгоритмов:
Первая часть — текстовая — является пояснением, а мнемокод — указанием на типовой алгоритм. Предполагается, что на этом этапе студент уже усвоил процедуры, связанные с представлением основных геометрических образов и условий на чертеже, и способен осуществлять их без посторонней помощи. Обмен информацией между студентом и преподавателем на этом этапе уже осуществляется в терминах стереометрии. На практике даже к концу обучения далеко не все студенты отличают алгоритм решения от процедуры представления объектов на чертеже, но и в этом случае дело не в алгоритмах.
4.
Рассмотрим особенности конструктивных задач, имеющие непосредственное отношение к НГ.
4.1. Конструктивные задачи решаются некоторым набором инструментов — основываются на элементарных построениях, из которых составляются более сложные алгоритмы [14, 26, 27]. Наборы инструментов могут быть различны, и студенты должны быть готовы к этому. Если для решения задач НГ они, как правило, используют линейку, угольник и циркуль, то, начиная работать в Компасе, обнаруживают целый ворох незнакомых кнопок. Для нас принципиально важно обеспечить, чтобы в их арсенале был базовый набор операций, на которые можно ссылаться как на алгоритмы, рассмотренные в п. 3.
Такими операциями являются:
На практике это означает, что необходимо заставить студента несколько раз выполнить каждое из этих построений и создать, таким образом, ассоциативную связь с понятием, к которому впоследствии предстоит неоднократно обращаться. В действительности некоторые студенты не умеют пользоваться циркулем или угольником. Ни о какой пользе алгоритмов нельзя говорить, если студент не владеет элементарными построениями, из которых составляется алгоритм.
После усвоения базовых операций можно предложить студенту решить те же задачи другими инструментами, например, разделить отрезок пополам при помощи только угольника (банковской карты), тем более, что студенты постоянно забывают свои инструменты. В алгоритмах будет использоваться обобщенный символ СЕРЕД, предоставляя выбор студенту.
Практический смысл этих действий состоит в том, чтобы на простых примерах показать многообразие путей решения той или иной задачи. Параллельно решается еще одна задача — воспитание уважения к точности построений. Практика показывает, что очень сложно побороть геометрическую небрежность, свойственную некоторым студентам, которая, если не сделать это в отношении ручного чертежа, только усугубляется при использовании CAD-систем.
В п. 3.2 был использован термин «неопределяемое понятие». К неопределяемым будем относить элементарные построения и, по аналогии, элементарные измерения и элементарные обозначения. Практически необходимо, чтобы каждое такое понятие (элементарное действие) подкреплялось точным узнаванием соответствующей механической процедуры.
4.2.
Метод решения конструктивных задач, называемый методом геометрических мест (ГМ), имеет с алгоритмизацией решений задач самую тесную связь [10, 11]. Суть метода заключается в том, что каждое из геометрических условий (прохождение через точку, принадлежность, параллельность и др.) используется для определения множества геометрических объектов, заведомо содержащего искомый, который затем находится как пересечение всех множеств.
Общий алгоритм выглядит следующим образом. Пусть A – искомый объект, B1, …, Bn – исходные объекты, и R1, …, Rk – условия. Тогда решение состоит в следующем:
И, поскольку пересечение множеств осуществляют попарно, тот или иной ход решения определяется способом расстановки скобок в последнем выражении.
Явно или неявно этот метод всегда используется при решении задач. Например, в примере 2 на этапе анализа были сформированы условия, которые определяют геометрические места — соответствующие плоскости уровня, пересечение которых и дает искомый объект. Традиционные построения на чертеже (линии связи) суть необозначенные образы этих плоскостей (рис. 2, в).
Пример 4. Рассмотрим с точки зрения ГМ построение прямой n, перпендикулярной плоскости α через заданную точку A (табл. 5).
Для моделирования связки K1 на чертеже достаточно проекций точки A, связки K2 – требуется какая-то прямая p связки, чтобы можно было построить n || p. Пересечение связок K1 ∩ K2 как таковое не рассматривается в начертательной геометрии и требует интерпретации в виде алгоритма. Не углубляясь в рассмотрение соответствий, лежащих за свойством перпендикулярности прямой и плоскости, воспользуемся известной теоремой стереометрии – p должна быть перпендикулярна двум произвольным пересекающимся прямым α. Пусть k и m – эти прямые, тогда выделить p можно следующим образом: p = κ(┴k) ∩ μ(┴m), где κ и μ – соответственно, перпендикулярные им плоскости – плоские поля, каждая прямая которых перпендикулярна k или m, соответственно. Наконец, для построения κ и μ проще всего выбрать в α две прямые уровня. И, поскольку таких плоскостей имеется ∞1 и для κ, и для μ, то плоскости удобно провести через точку A. Тогда n ≡ p. Чертеж для фронтально-проецирующей плоскости α показан на рис. 2, г.
Таким образом «привычные» способы решения задач реализуют способ геометрических мест, но делают это, не вдаваясь в «геометрические детали». Может быть, потому, что от грамматики чертежа большего не требуется?
Для нас наиболее интересным является тот факт, что имея алгоритмические реализации операторов построения ГМ (Ф1, …) и операторов пересечения ГМ (F1 ∩ …) мы легко получаем решение целого класса геометрических задач, поскольку метод ГМ один из самых простых в формализации и понимании.
4.3. Другим известным методом решения задач является использование геометрических преобразований (ГП). Общий алгоритм решения в этом случае включает:
Выбор преобразования T, переводящего исходные объекты B1, …, Bn в объекты B'1, …, B'n, для которых способ решения задачи известен.
Преобразование объектов:
Решение задачи для преобразованных объектов A' = F (B'1, …, B'n).
При необходимости обратное преобразование: A = T-1 (A).
Этот способ предполагает многократное использование одной и той же последовательности построений для разных объектов при выполнении прямого (T) и обратного преобразования (T-1) и также тесно связан с повторным выполнением групп построений.
4.4. В схеме на рис. 1 блок анализа изображен как условный. Выше было показано, что на этапе анализа задается множество вопросов, ответы на которые в полной мере управляют составлением и выбором алгоритма для решения задачи.
При этом две формально одинаковые задачи могут решаться по-разному. Например кривая второго порядка имеет с прямой в точности две точки пересечения — действительные различные, совпавшие или мнимые. Чтобы построить эти точки, требуются различные алгоритмы. Подобная ситуация наблюдается в НГ, где одни и те же задачи решаются иначе для объектов частного и общего положения. Причина здесь не в том, что объекты проявляют различные взаимные свойства, но в способах выражения тех или иных свойств, которые невозможно выразить единообразно. Так, на расширенной евклидовой плоскости пересечение прямых в собственной точке выражается их пересечением, в несобственной — параллельностью; проецирующая прямая изображается прямой и точкой, в общем случае — двумя прямыми и др. Все это свидетельствует о грамматический природе решений конструктивных задач и требует соответствующего анализа контекста при решении, и, как следствие, явного или неявного алгоритма. На рис. 3 приведен алгоритм определения расстояния от точки до плоскости, методом структурной декомпозиции решения разделенный на более простые и элементарные.
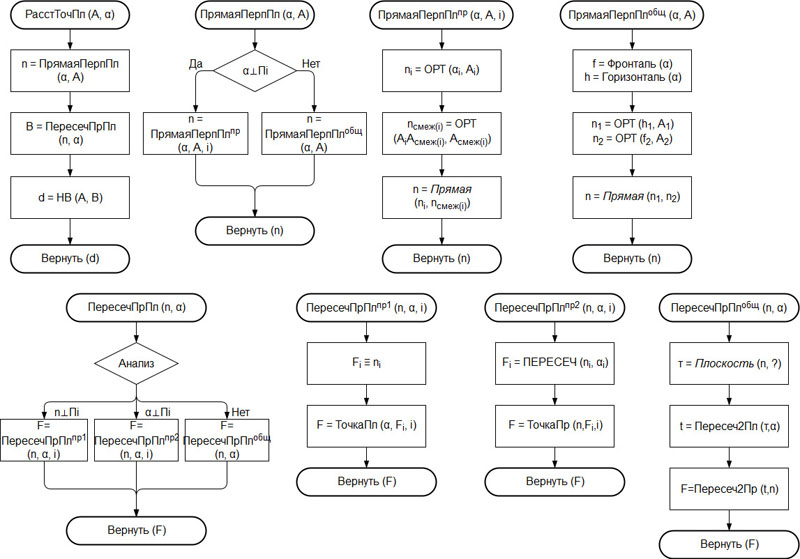
Рис. 3
Появление вариантов является закономерным результатом применения схемы на рис. 1, где обратная связь после блока доказательства после всякой неудачной попытки заставляет возвращаться к началу и искать новые пути решения. В этом смысле схемы на рис. 3 формализуют алгоритмические схемы, которые сами собой формируются в мозгу человека, решающего графические задачи, осознает он это или нет.
В п.4.1 было также показано, что для решения одной и той же задачи могут использоваться различные частные алгоритмы, и на этапе анализа должен выполняться по тем или иным соображениям один из них. В п. 4.3. первый этап применения ГП состоит в выборе подходящего преобразования, который также должен осуществляться на этапе анализа.
Таким образом, алгоритмизация ни в коей мере не уменьшает важность знания геометрии или понимания геометрического содержания задачи и используемых методов, но смещает акценты на первый этап решения задач — этап анализа, на котором принимаются стратегические решения и выбирается основной способ.
При этом положительные свойства алгоритмизации проявляются как: 1) приобретение навыка разбиения задач на подзадачи, 2) приобретения навыка составления решения задачи из элементарных. Последовательное построение и накопление алгоритмов дает возможность решать все более сложные задачи [5]. К тому же, в этом качестве начертательная геометрия приобретает междисциплинарные связи с программированием.
5. Рассмотренные аспекты алгоритмизации начертательной геометрии позволяют сделать вывод о том, что алгоритмы и алгоритмизация не могут считаться причиной снижения уровня понимания геометрии и ослабления пространственного воображения. Основными причинами того, что алгоритмизация в учебном процессе по начертательной геометрии негативно сказывается на учебном процессе мы считаем следующие:
Одновременно с этим базовой проблемой геометро-графического образования является недостаток и сокращение часов на изучение дисциплин. Время нужно для механизации элементарных действий и овладения терминологией, для адаптации к алгоритмическому подходу, для составления таблиц, для разбора лекций, для решения задач, наконец. В старых сборниках - Арустамова, Гордона и др. - содержится 200-400 задач. Сколько в действительности решает современный студент? В [31] со ссылкой на «Лекции о развитии математики в XIX столетии» Ф. Клейна отмечается, что в первые десятилетия Политехнической школы в Париже учебным планом для начертательной геометрии отводилось 153 лекции по 1,5 часа. Там же говорится о курсах в 18 лекций по данным 1976 года. Где эти 18 лекций сегодня?
Факт заключается в том, что на первом курсе технического вуза студентам предлагается изучить новый для них графический язык и полностью им овладеть за два семестра при катастрофическом недостатке часов. При этом язык алгебры, русский или иностранный языки изучаются в течение нескольких лет. В таких условиях просто нельзя в силу объективных свойств информации и когнитивных особенностей человека кардинально изменить понимание, запоминание, наработку практического навыка. В конце концов для развития пространственного воображения необходимо просто много работать с изображениями. Но это много не обеспечено «живыми» часами. СРС не в счет.
В таких условиях именно алгоритмизация имеет имеет не выработанный пока ресурс — за счет структурных связей оперировать компактными и потому более легкими для запоминания и понимания алгоритмами, что на фоне развития и внедрения компьютерных технологий автоматизированного конструктивного моделирования дает надежду сохранить главное в геометро-графическом образовании.
1. Жирных Б. Г. Формальная логика и алгоритмы в преподавании начертательной геометрии / Б. Г. Жирных [и др.]. URL: http://dgng.pstu.ru/conf2017/papers/61
2. Иловайский Л. В. Развивать образное мышление студентов // Сборник науч.-метод.статей по НГ и ИГ. Вып. 2. М.: Высшая школа, 1974. С. 37-40
3. Маркова А. П. Обучение студентов составлению алгоритмов решения задач инженерной графики // Сборник науч.-метод.статей по НГ и ИГ. Вып. 3. М.: Высшая школа, 1976. С. 8-13.
4. Бородкина С. И. Обобщенные алгоритмы решения задач начертательной геометрии // Там же. С. 13-19.
5. Котов И. И., Полозов В. С. Методика планирования и организации метериала в преподавании начертательной геометрии и черчения // Сборник науч.-метод.статей по НГ и ИГ. Вып. 4. М.: Высшая школа, 1977. С. 4-10
6. Белосельская В. Д. Формирование системы приемов умственной деятельности студентов при изучении курса начертательной геометрии // Сборник науч.-метод.статей по НГ и ИГ. Вып. 6. М.: Высшая школа, 1978. С. 6-10
7. Михайленко В. Е., Анпилогова В. А. О применении ЭВМ в преподавании начертательной геометрии // Там же. С. 10-13
8. Гирш А. Г. О позиционных задачах // Там же. С. 33-37.
9. Ларин М. Д. Учебные алгоритмы как средство управления деятельностью студентов при обучении решению задач // Сборник науч.-метод.статей по НГ и ИГ. Вып. 13. М.: Высшая школа, 1986. С. 76-80
10. Глоговский В. В., Гринева Б. М., Гнатюк М. О. Начертательная геометрия на алгоритмической основе. Львов: Вища школа, 1978. 148 с.
11. Курс начертательной геометрии на основе геометрического моделирования / В. Я. Волков [и др.]. Омск: СибАДИ, 2010. 256 с.
12. Курс начертательной геометрии с алгоритмами для ЭВМ / Л. Г. Нартова [и др.]. М.: МАИ, 1994. 253 с.
13. Иванов Г. С. Начертательная геометрия. М.: МГУ Леса, 2012. 340 с.
14. Аргунов Б. И., Балк М. Б. Геометрические построения на плоскости. М., 1957. 268 с.
15. Пеклич В. А., Павленко С. Н. Задачи по начертательной геометрии. М.: Высшая школа, 1999. 140 с.
16. Короткий В. А. Проективное построение коники. Челябинск, 2010. 94 с.
17. Шлыгин В. В. Графические методы расчетов в машиностроении. М.: Машиностроение, 1967. 288 с.
18. Труды Московского научно-методического семинара по начертательной геометрии и инженерной графике. Выпуск 2. М., 1963. 332 с.
19. Киселевич А. Д. Алгоритмы машинного проектирования в курсе машиностроительного черчения / А. Д. Киселевич [и др.] // Сборник науч.-метод.статей по НГ и ИГ. Вып. 3. М.: Высшая школа, 1976. С. 34-45.
20. Хопкрофт, Дж. Введение в теорию автоматов, языков и вычислений / Дж. Хопкрофт, Р. Мотвани, Дж. Ульман. М.: Вильямс, 2008. 528 с.
21. Гилой, В. Интерактивная машинная графика: Структуры данных, алгоритмы, языки / В. Гилой. М.: Мир, 1981. 384 с.
22. Ньюмен, У. Основы интерактивной машинной графики / У. Ньюмен, Р. Спрулл. М.: Мир, 1976. 576 с.
23. Начертательная геометрия / Д. З. Есхожин [и др.]. Акмола: АСХИ, 1992. 144 с.
24. Волошинов, Д. В. Конструктивное геометрическое моделирование / Д. В. Волошинов. – Saarbrucken: Lambert Academic Publishing, 2010. 355 с.
25. Волошинов Д. В. Геометрическая лаборатория. Новый геометрический инструмент. URL: http://dgng.pstu.ru/conf2017/papers/60
26. Глоговский В. В. Элементарные конструктивные задачи по начертательной геометрии. Львов, 1981. 156 с.
27. Четверухин Н. Ф. Методы геометрических построений. М.: Учпедгиз, 1952. 148 с.
28. Каган В. Ф. Очерки по геометрии. М., 1963. С. 42-48.
29. Пеклич, В. А. Высшая начертательная геометрия / В. А. Пеклич. М.: АСВ, 2000. 344 с.
30. Панчук К.Л., Кайгородцева Н.В. Элементы циклографической начертательной геометрии // GraphiCon 2016. Труды Международной научной конференции. – Москва-Протвино, 2016. – С. 69–71.
31. Королевич А. И. Элементы теории информации в геометрии графического отображения // Сборник науч.-метод.статей по НГ и ИГ. Вып. 3. М.: Высшая школа, 1976. С. 66-69
Тихонов-Бугров Дмитрий Евгеньевич (26 марта 2017 г. 14:15) |
Здравствуйте, Алексей Александрович! Очень рад Вашему появлению на конференции хотя бы под занавес. Часто задавая себе вопрос: а где же Бойков?, преполагал, что занят диссертацией. Теперь по существу вопроса. Полностью согласен с Вашими выводами по п.5, но и не вижу противоречий с авторами доклада 1: "тупая алгоритмизация" не должна тормозить развития рефлексии. Спасибо за тщательную проработку вопроса. Г. Монж как раз и советовал "тщиться и стараться". С уважением, Тихонов-Бугров. |
|
Бойков Алексей Александрович (26 марта 2017 г. 21:34) |
Здравствуйте, Дмитрий Евгеньевич! Спасибо за высокую оценку. Я был где-то здесь. Действительно, занят диссертацией и еще студенческой конференцией "Энергия-2017", которую в этом году добровольно-принудительно поручили мне. Насчет доклада 1 противорчеия, скорее, на уровне введения и названия. При пристальном чтении его, я заподозрил истинные причины проблемы - "мы сталкиваемся с постоянным сокращением времени", "мы вынуждены работать в режиме нарастающей интенсификации", "сколько времени уходит на то, чтобы студенты вспомнили и перечислили свойства квадрата" и др., не имеющие, строго говоря, отношения к "формальной логике и алгоритмам". Настоящий доклад для меня - попытка разобраться "с холодной головой".
С уважением, А.Бойков |
Кокарева Яна Андреевна (29 марта 2017 г. 19:37) |
Алексей Александрович, спасибо за Ваш доклад. По-моему, вполне удачная "попытка разобраться с "холодной головой". Понравился пример: "За каждым из этих понятий стоит свое определение, но при упрощении выражения вроде sin4α + cos4α или sin4105∘⋅cos475∘ задумываться о том, что синус есть отношение противолежащего катета к гипотенузе в прямоугольном треугольнике, — излишне и даже вредно". Согласна с Вашим взглядом на эту проблему. С уважением, Кокарева Я.А. |
|
Бойков Алексей Александрович (30 марта 2017 г. 16:43) |
Здравствуйте, Яна! Спасибо за высокую оценку. С уважением, А.Бойков |