О НАГЛЯДНОСТИ МОДЕЛИРОВАНИЯ В ПРОСТРАНСТВЕ БОЛЕЕ ТРЕХ ИЗМЕРЕНИЙ

В статье рассматривается понятие наглядности применительно к многомерному геометрическому моделированию и подход, обеспечивающий возможность решения задач с объектами многомерных пространств.

1.

Неоднократно отмечалось, что в геометро-графическом образовании имеется противоречие между возможностями используемых в обучении инструментов и требованиями к инструментам при решении ряда учебных и прикладных задач [1, 2, 3]. Ярким свидетельством тому может служить дискуссия, вызванная докладом [4] прошлой конференции, где при включении в курс «Наглядной инженерной геометрии» элементов моделирования многомерных пространств, многомерная составляющая оказалась в полной зависимости от систем геометрического моделирования, по сути своей не приспособленных для работы с пространствами более трех измерений.

В настоящей работе будет сделан краткий анализ понятия наглядности в контексте многомерного моделирования и предложен подход, обеспечивающий свободу моделирования пространств более трех измерений.

2.

Объектами плоского геометрического моделирования выступают точки, линии, n-угольники (в том числе с криволинейными сторонами). При этом все объекты представлены предельно наглядно — в натуральную величину, когда любые геометрические свойства могут быть показаны и проверены непосредственно.

Объектами трехмерного геометрического моделирования выступают точки, линии, поверхности и тела. Уже трехмерное геометрическое моделирование сопровождается частичной потерей наглядности, поскольку объекты моделирования представлены наблюдателю в любой отдельно взятый момент времени одной своей стороной (в виде проекции), натуральные величины плоских объектов проявляются только при их частном расположении, натуральной величиной всякого трехмерного объекта является сам объект, объекты обладают способностью перекрывать друг друга, отчего возникают «скрытые» части, возможны оптические коллизии. Так, перпендикулярность двух прямых в пространстве вряд ли можно считать наглядной для произвольного расположения наблюдателя относительно объектов. Проверка геометрических свойств во многих случаях не может быть выполнена без дополнительных приемов. Наиболее простым из них является использование нескольких изображений, разделенных в пространстве (многовидовые чертежи, серии сечений и др.) или времени (анимации, повороты объекта, перемещение вокруг него).

При переходе к пространствам измерений более трех по понятным причинам теряется сама возможность воспринимать объект моделирования непосредственно. Чтобы обеспечить восприятие, объект приходится «возвращать» в трехмерное пространство проецированием, сечением или развертыванием. В любом случае непосредственному (наглядному) восприятию оказывается доступна только часть моделируемого пространства с оказавшимися в ней объектами.

В какой мере возможно говорить о наглядности многомерного геометрического моделирования? Мы будем пользоваться определением, приведенным в [5]: наглядность — это свойство модели-изображения вызывать в мозгу человека зрительный образ моделируемых признаков объекта-оригинала.

Модели-изображения в зависимости от функции можно разделить на знаковые и образные [5]. Знаковые — представляют собой совокупность знаков, используемых для отражения свойств моделируемого объекта. В этом случае наглядность определяется как однозначность и полнота информации, сообщаемой моделью. Правильность прочтения этой информации определяется также знанием человеком соответствующей системы знаков. Под образной моделью понимается модель, функция которой состоит в формировании в мозгу человека идеального образа моделируемого объекта — образа, максимально приближенного к образу, возникающему при рассматривании самого объекта. Большая или меньшая наглядность в этом случае — большее или меньшее соответствие этому образу.

Очевидно, объекты многомерных пространств не имеют физического воплощения. Отдельной задачей многомерного моделирования может быть поиск образов для представления информации о геометрических объектах многомерных пространств. Однако в контексте «инженерной геометрии» мы склоняемся к тому, чтобы рассматривать модели многомерных пространств и объектов как знаковые. В этом случае прикладной характер моделей выходит на передний план.

3.

В математическом моделировании, частью которого является геометрическое, ярко выражены два дополняющих друг друга подхода — аналитический, связанный с представлением моделируемых объектов через наборы числовых величин и алгебраических зависимостей между ними, и конструктивный (синтетический), связанный с представлением моделируемых объектов через другие объекты, находящиеся с оригиналами в некоторой непрерывной зависимости [6, 7, 8]. Очевидно, наглядность при геометрическом моделировании возможна лишь в случае преобладания второго подхода, и только если объекты, используемые для представления моделируемых оригиналов, доступны для наглядного (непосредственного) восприятия. Таким образом, наглядное моделирование многомерных пространств и объектов возможно лишь при представлении их пространствами и объектами двух или трех измерений. Как отмечалось ранее, геометрические свойства объектов, их натуральная величина и др. наиболее наглядно представляются при помощи плоских изображений.

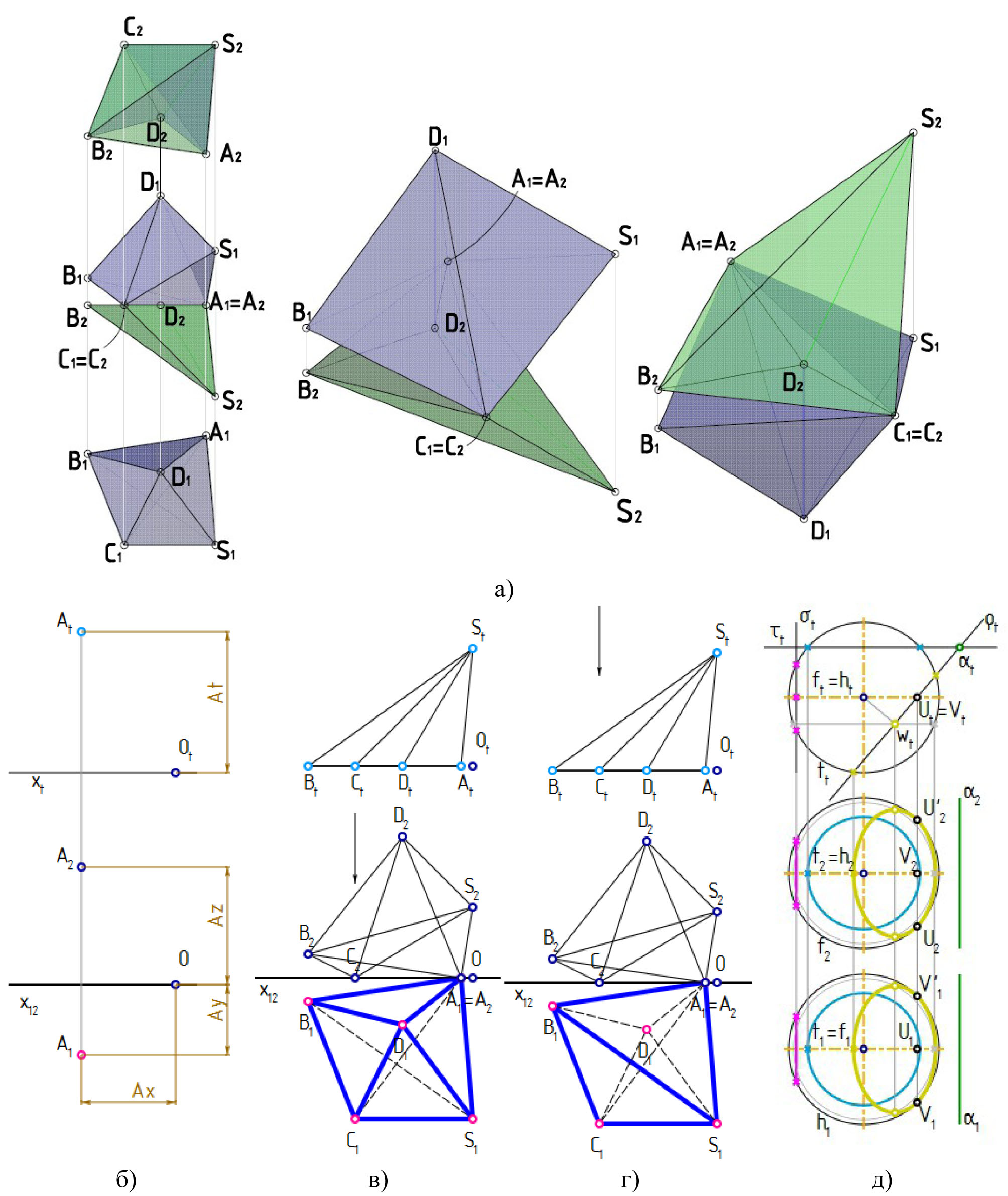
В качестве примера, сравним пару ортогональных трехмерных проекций четырехмерной фигуры в пространства Е₁ (OXYZ) и Е₂ (OXYT) (рис. 1, а) — трехмерный аналог чертежа Монжа (модель построена в AutoCAD'е) — и совокупность ее ортогональных плоских проекций (рис. 1, в-г). Можно заметить, что проекция D₂ точки D «прилипла» к основанию объекта вместе с содержащими ее ребрами и гранями, а проекция B₁S₁ ребра BC с соответствующими гранями «погрузилась внутрь» объекта. У трехмерного представления даже с полной свободой получить любую проекцию (вращая модель) трудно найти какие-то особенные преимущества перед изначально плоским.

Моделирование многомерных пространств и объектов при помощи плоских изображений является предметом начертательной геометрии многомерных пространств и предлагает широкий круг разнообразных методов [1, 6, 9-12]; среди них:

• гиперэпюр В. П. Радищева, на котором все проекции точки лежат на общей линии связи;
• чертеж Скоуте, на котором каждая пара смежных проекций точки лежит на своей линии связи;
• векторные проекции Е. С. Федорова и их модификации;
• параллельные аксонометрии объектов многомерного пространства и др.

Каждый из них позволяет обратимо моделировать точки многомерного пространства и предлагает различные подходы к моделированию прямых, плоскостей, гиперплоскостей и др., для большинства — исследованы и описаны способы решения метрических и позиционных задач, способы преобразования чертежа и объектов пространства.

Сущность «наглядности» в этом случае трансформируется в: а) возможность наблюдать или проверять свойства плоских объектов; б) возможность по совокупности их свойств делать выводы о свойствах моделируемого многомерного объекта.

Пусть точка описывается координатами X, Y, Z, T; для ее обратимого моделирования требуется комбинация объектов плоскости чертежа с четырьмя степенями свободы. Будем использовать ортогональный чертеж (гиперэпюр Радищева) в системе плоскостей проекций П₁ (XOY), П₂ (XOZ) и П_t (XOT), который строится, как показано на рис. 1, б. Такой метод обладает рядом достоинств:

• ортогональное проецирование выполняется так же, как при образовании эпюра Монжа трехмерного пространства, что согласуется с имеющимся у студента опытом;
• все проекции точки лежат на вертикальной линии связи;
• сохраняются свойства принадлежности точки линиям, параллельности прямых и др.;
• правило прямоугольного треугольника выполняется подобно трехмерному случаю;
• прямые, плоскости и пространства частного положения ведут себя во многом подобно прямым и плоскостям частного положения трехмерного пространства и др.

Чертеж наглядно демонстрирует некоторые свойства объектов 4-пространства:

• всякая точка в поле какой-либо плоскости проекций является проекцией той или иной особой проецирующей плоскости [11]; как следствие плоскости проекций имеют вырожденные проекции в виде точки на других плоскостях проекций;
• видимость не может быть определена однозначно, требуется указание направления взгляда (имеется ∞¹ таких направлений в плоскости, перпендикулярной картинной), например, на рис. 1, в-г показана видимость при взгляде вдоль OZ и OT, соответственно;
• точка и прямая задаются тремя проекциями, плоскость может иметь проекцию в виде точки (особая проецирующая плоскость), пару проекций в виде прямых, одну проекцию в виде прямой или не иметь таких проекций; трехмерное пространство может иметь вырожденную проекцию в виде прямой и др.

4.

Будем предполагать у студента средний уровень знания элементарной геометрии и владения методами начертательной геометрии. Он не только необходим [13], но и закреплен в требованиях образовательного стандарта [14]. Будем считать наглядным такой способ постановки и решения задач, при котором по возможности большее число геометрических свойств моделируемых объектов согласовывалось бы с имеющимся у студента опытом плоского и трехмерного геометрического моделирования.

Именно ортогональный чертеж дает студенту способ решения многих геометрических задач с объектами 4-пространства, при этом сохраняется «наглядность» многомерного моделирования в том смысле, что многие элементы на чертеже остаются узнаваемы и понятны, и не требуется обращение к уравнениям и формулам. Так, свойства чертежа не зависят от присутствия на нем координатных осей, и он может быть задан вообще без обращения к аналитическому методу (без координат точек).

При обсуждении на факультативе элементов многомерного моделирования понимание гиперэпюра не вызывает заметных сложностей. Так, например, четырехмерный шар (рис. 1, д) в системе плоскостей XOY/XOZ/XOT имеет три контура — горизонтальный (h), фронтальный (f) и t-контур (t), проекции которых на каждой из плоскостей попарно совпадают. Гиперэпюр позволяет наглядно показать образование сечений четырехмерных объектов и проанализировать, как эти сечения проецируются в привычное трехмерное пространство OXYZ. На рис. 1, д показаны сечения четырехмерного шара трехмерными пространствами частного положения ρ, σ и τ; являясь трехмерными шарами, сечения проецируются в пространство OXYZ по-разному. Шар в сечении пространством σ сжимается в двойной круг (показан розовым); его параллели в плоскостях, перпендикулярных OX, различаются t-координатой, а в пространстве OXYZ представляют собой концентрические окружности. Шар в сечении пространством τ, занимающим положение уровня, проецируется в пространство OXYZ в натуральную величину; голубые окружности — его очерки. Шар в сечении пространством ρ проецируется с искажением, в виде сжатого эллипсоида; золотистые эллипсы — очерки. Пространства ρ и τ пересекаются по общей профильной плоскости α, имеющей на плоскости XOT проекцию в виде точки. Всякая плоская фигура может иметь проекцию в виде точки. Например, w_t — проекция окружности, которая на плоскость YOZ проецировалась бы в натуральную величину. Точки U и V, t-проекции которых совпали, лежат на контурах f и h, соответственно (подробнее о поверхностях в многомерных пространствах, например, в [Первикова В.Н., Коробова Д.М., Решетникова А.А. Чертежи поверхностей n-мерного пространства и их инженерные приложения // Геометрические преобразования и прикладная многомерная геометрия. Труды МАИ. Вып. 271. М., 1973. С. 68-87]).

5.

Решение задач с объектами многомерного пространства вручную может быть весьма трудоемким. Требуются средства автоматизации, приспособленные для работы с такими объектами. Традиционные системы трехмерного геометрического моделирования для решения таких задач приспособлены так же плохо, как для решения задач в неевклидовых пространствах. Использование «электронных кульманов» типа Компас-График или AutoCAD (без средств программирования) равносильно решению вручную.

Средства автоматизации должны предоставлять возможность быстро выполнять группы однотипных построений произвольной сложности.

Далее в примерах будем записывать построения и их последовательности подобно операторам языка ФАП-КП [15]: объект = символ построения (опорные объекты или значения параметров). Такая запись отличается от общепринятой математической, но однозначно показывает, что является результатом построения.

Ключевую роль играет составное построение — последовательность построений, составных или элементарных, которые при решении задачи выполняются как одно. Для определения составного построения будем использовать запись вида:

Следующие построения и измерения будем использовать в качестве элементарных:

Построение чертежа 4-точки выполняет следующая последовательность:

Построение проекций отрезка:

Пусть требуется построить чертеж 4-пирамиды с тетраэдром в основании по координатам ее вершин:

Введем для удобства построение недостающей проекции точки на прямой:

6.

Рассмотрим построение натуральной величины сечения 4-пирамиды пространством частного положения τ (рис. 2, а).

Выполним пересечение τ (объект taut) с ребрами пирамиды:

Выполним плоско-параллельный перенос [12], тогда в пространстве OXYZ окажется натуральная величина сечения (вместо надчеркивания смещенные проекции помечены верхним индексом 1).

tm = trmv (taut : taust) // объект-преобразователь движения

Выполним обводку проекций ребер:

edge2 (A,B:thick,dashed,dashed)

...

Полученное изображение сечения в трех проекциях является полноценной трехмерной моделью, поскольку может быть преобразовано в соответствующую трехмерную модель [16, 17], передано в трехмерный редактор или напечатано на 3D-принтере.

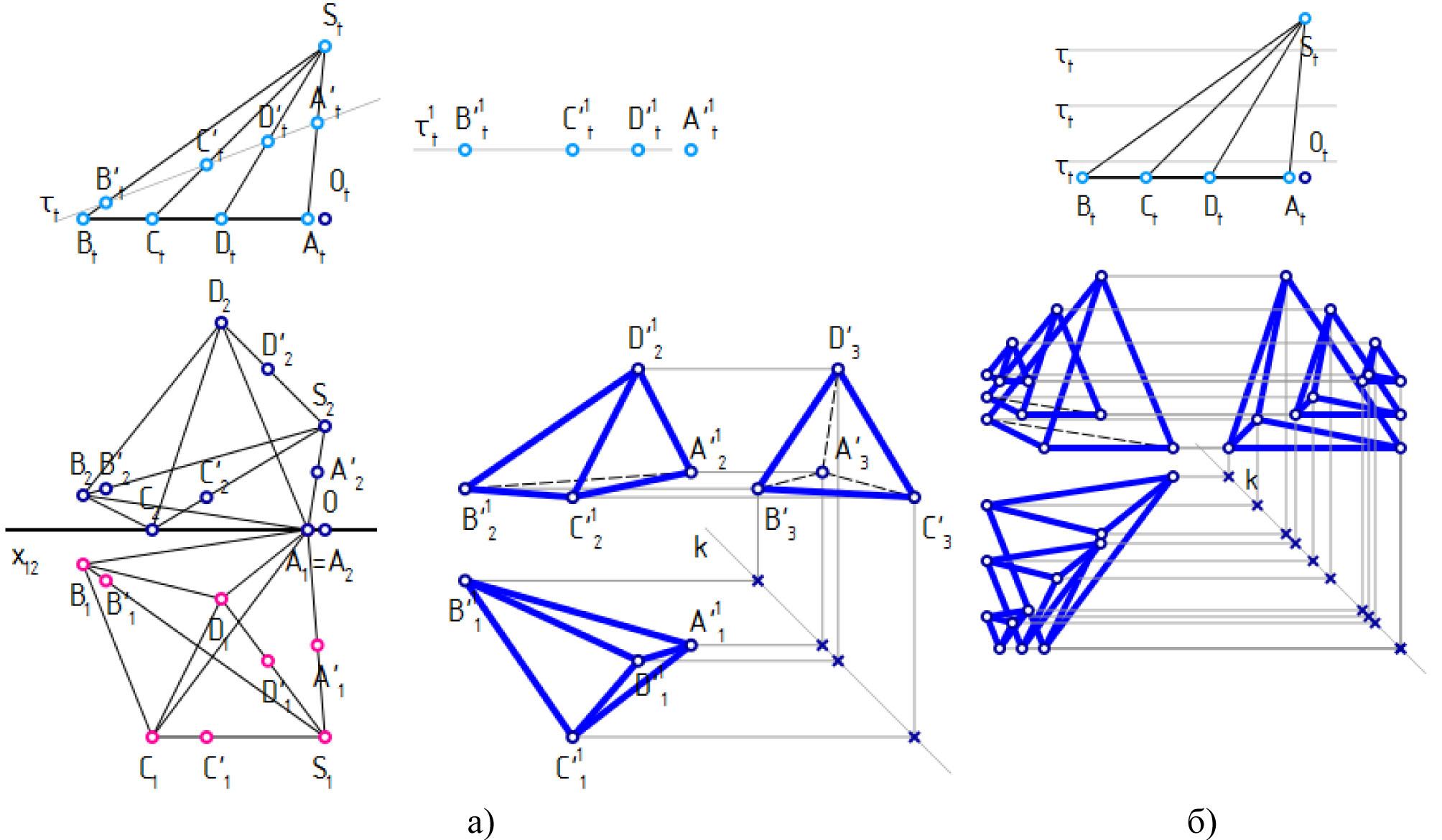
Рис. 2. Сечение четырехмерной пирамиды гиперплоскостью (трехмерным пространством) частного положения τ

Меняя положение τ в цикле, можем получить серию сечений пирамиды (на рис. 2, б сечения смещены для наглядности).

7.

Поскольку в [4] один из разделов планируемого курса связан с развертыванием многомерных n-гранников, рассмотрим построение развертки боковой поверхности четырехмерной пирамиды, считая, что она усечена пространством τ (рис. 2, а). В основании пирамиды лежит тетраэдр ABCD, боковые стороны — тетраэдры SABC, SBCD, SABD, SACD. Тетраэдр всегда можно построить по натуральной величине его ребер. Развернем боковую поверхность исходной пирамиды, затем усечем соответствующие ребра.

При помощи правила прямоугольного треугольника найдем длины сторон (рис. 3, а):

end sub

Измерение натуральных величин сторон выглядит так:

dAS = len(A,S)

...

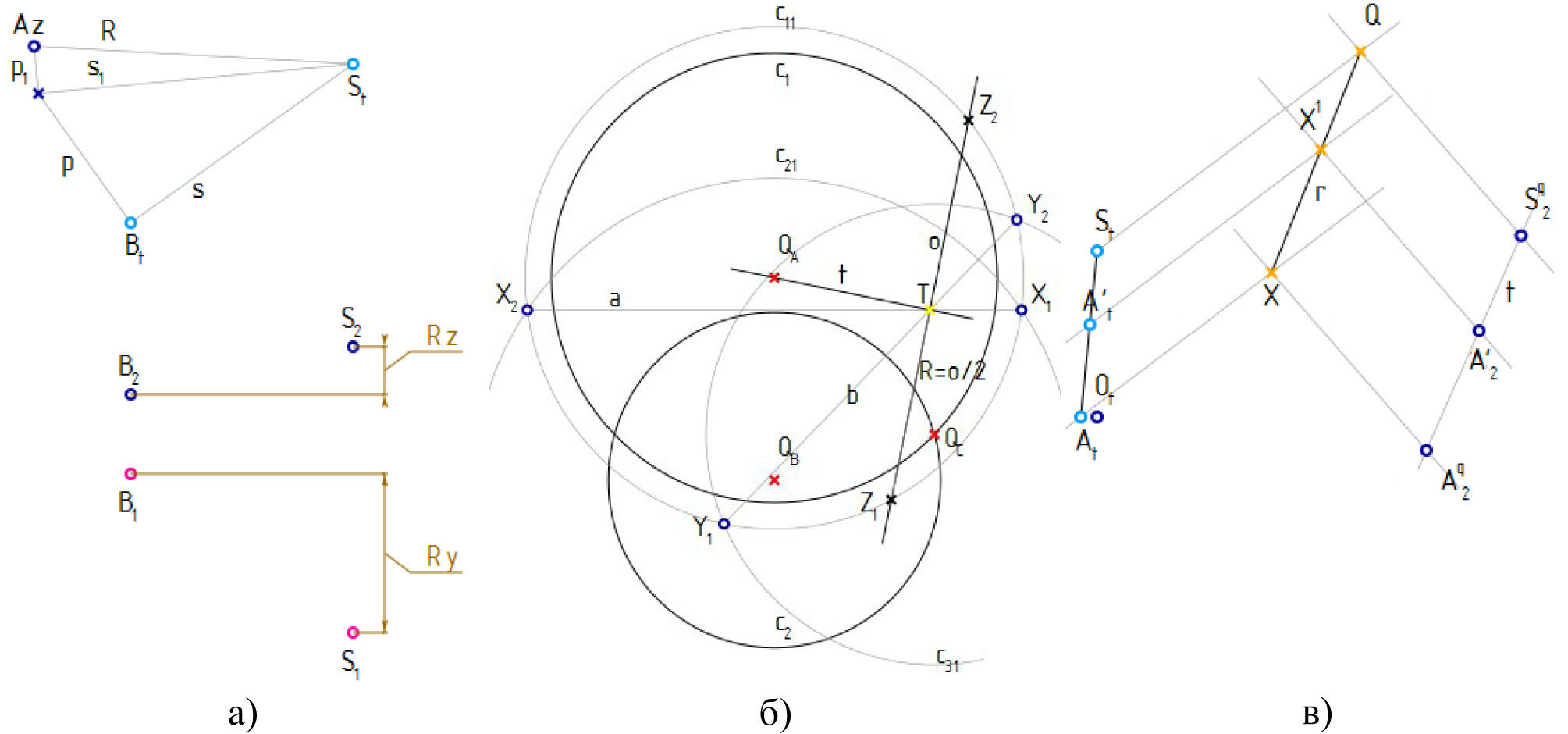
Рис. 3. Составные построения к примеру с построением развертки

Для построения каждой трехмерной стороны исходной пирамиды требуется многократно находить точки на заданном расстоянии от трех данных, что, в общем случае, требует пересечения трех сфер с произвольно расположенными центрами.

В случае, когда центры лежат в горизонтальной плоскости, найти проекцию двух соответствующих точек и расстояние до них от плоскости, проведенной через центры сфер, довольно легко. Запишем соответствующее построение (рис. 3, б):

Если описать построение, откладывающее натуральную величину на проекциях прямой общего положения, и построение, которое проводит перпендикуляр к плоскости через точку, заданную одной проекцией (ort2), то построение четвертой точки тетраэдра по заданным трем для плоскости общего положения может быть выполнено следующими командами:

[Dx,hd] = p4th(Cq2,dAC : Sq2,dAS : Dq2,dAD : dCS,dDS,dCD)

[Ar1,Ar2,_,_] = ort2(Cq,Sq,Dq,Dx,hd) // построить перпендикуляр через точку плоскости, заданную проекцией Dx

// и сразу отложить hd, вернуть по две проекции каждой из двух возможных точек

Для переноса точки, делящей отрезок в заданном отношении, запишем построение divide (рис. 3, в). Тогда перенос точек основания пирамиды на развертку может быть выполнен так:

Достраиваем третью проекцию и обводим с учетом видимости, как в первом примере (рис. 4, а). Точки трехмерной развертки помечены верхними индексами q (при первом появлении) и r (при повторном).

Как и в случае с сечением, полученный трехвидовый чертеж является полноценной 3D-моделью, которая может быть передана в трехмерные редакторы или напечатана на 3D-принтере.

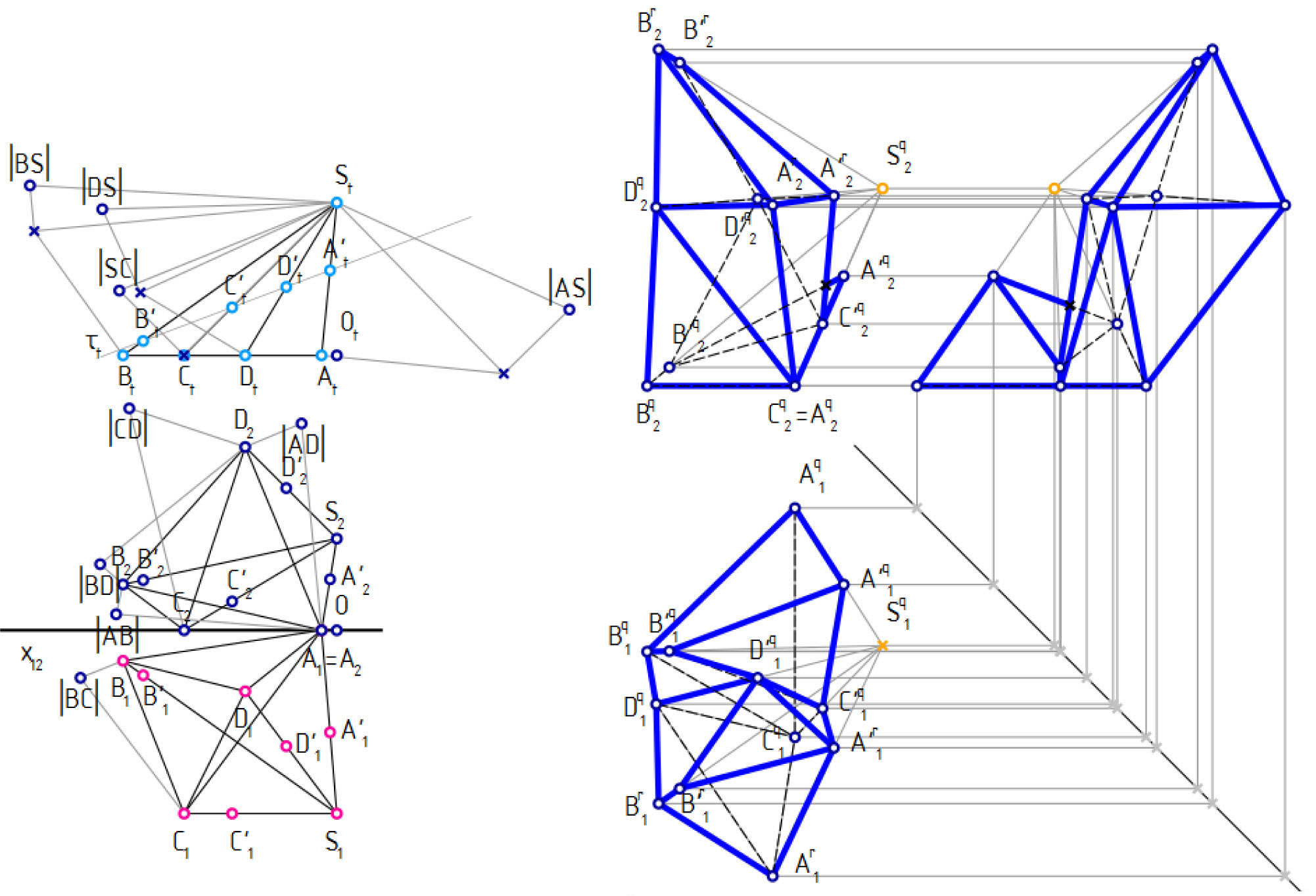
Рис. 4. Трехмерная развертка боковой поверхности пирамиды SABCD, усеченной гиперплоскостью τ

8.

Созданные составные построения можно использовать для решения задачи о построении приближенной трехмерной развертки поверхности четырехмерного конуса (с собственной или несобственной вершиной).

Замечание. Подобно тому, как обычный конус (тело) состоит из ∞² отрезков, соединяющих вершину с точками плоского основания, четырехмерный конус состоит из ∞³ отрезков, соединяющих вершину с точками трехмерного основания. Боковую поверхность обыкновенного конуса образуют те из ∞¹ отрезков, которые соединяют вершину с ∞¹ точками линии, ограничивающей основание. Боковую поверхность 4-конуса образуют те из ∞² отрезков, которые соединяют вершину с ∞² точками поверхности основания. Построение приближенной развертки обыкновенного конуса осуществляется заменой линии, ограничивающей основание, ломаной с заданной точностью. Такая замена, ввиду одномерности линии возможна всегда. Построение приближенной развертки 4-конуса требует аппроксимации поверхности трехмерного основания некоторой гранной поверхностью. Самый простой способ построения развертки - восставить на каждую из таких граней пирамиду, получив, таким образом, развертку в виде "звезды", подобно развертке обыкновенного конуса на рис. 5, а. Этот способ практически бесполезен, так как, в принципе, непрерывная боковая поверхность распадается на множество не связанных между собой "игл". Чтобы получить развертку в виде единой фигуры, необходимо, чтобы поверхность основания 4-конуса, в свою очередь, была развертываема.

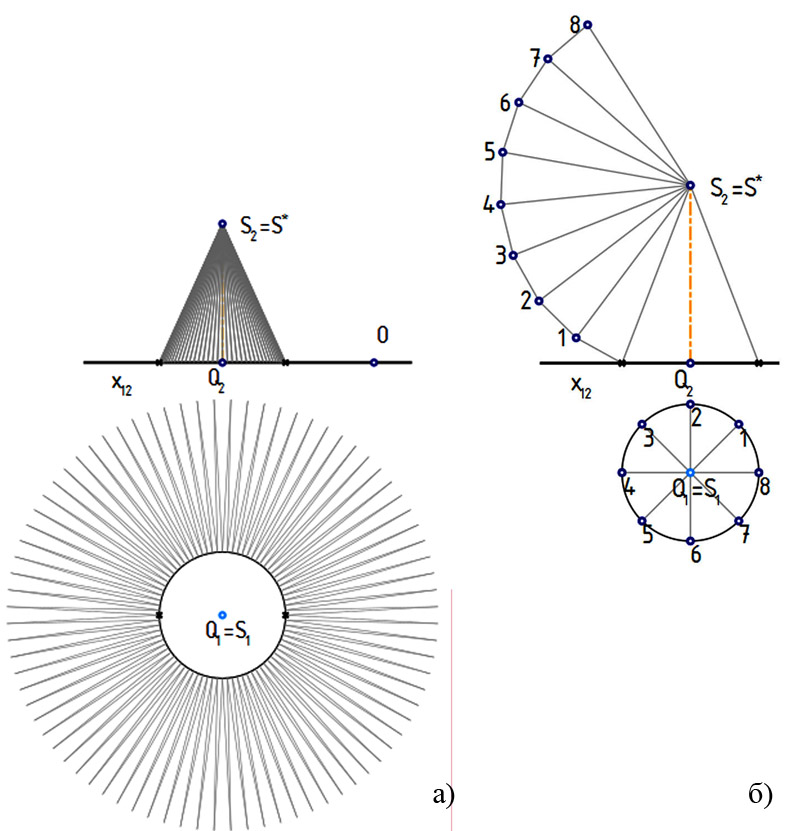
Рис. 5. Развертывание обыкновенного конуса

Рассмотрим развертывание 4-конуса с вершиной в точке S, в основании которого лежит обыкновенный конус μ с вершиной в точке D (рис. 6). Развертку 4-конуса составят - трехмерный конус μ (основание), трехмерный конус σ с вершиной в точке S на основании конуса μ, и коническая поверхность с вершиной S и боковой поверхностью μ в качестве основания. Если аппроксимировать боковую поверхность μ пирамидальной (μ'), тогда на каждой грани μ' может быть восставлен тетраэдр с вершиной в S. Так как D входит в каждую из боковых граней μ', - ребро DS является общим для всех тетраэдров.

Развертывание будет происходить подобно тому, как развертывается поверхность обыкновенного конуса (рис. 5, б): треугольники боковой поверхности аппроксимирующей пирамиды, имея смежные ребра, располагаются на плокости один за другим вокруг общей вершины S. В случае развертывания поверхности 4-конуса тетраэдры, имея смежные грани, будут располагаться в пространстве один за другим вокруг общего отрезка DS (на рис. 4 тетраэдры ABDS, BCDS, ACDS, имея общие грани, располагаются вокруг DS). Аналогично, в случае развертывания пятимерного конуса с некоторой вершиной R и рассмотренным 4-конусом в основании, 4-грани пятимерной аппроксимирующей пирамиды будут разворачиваться, имея попарно общие тетраэдры, вокруг общего треугольника RSD и т.п. Это дает достаточно простой конструктивный способ построения развертки. На рис. 6, а показан случай, когда 4-конус - прямой, на рис. 6, б - наклонный. Меняя число сторон аппроксимирующей пирамиды (в примере их 25), можно с той или иной точностью формировать каркас линий соответствующих поверхностей.

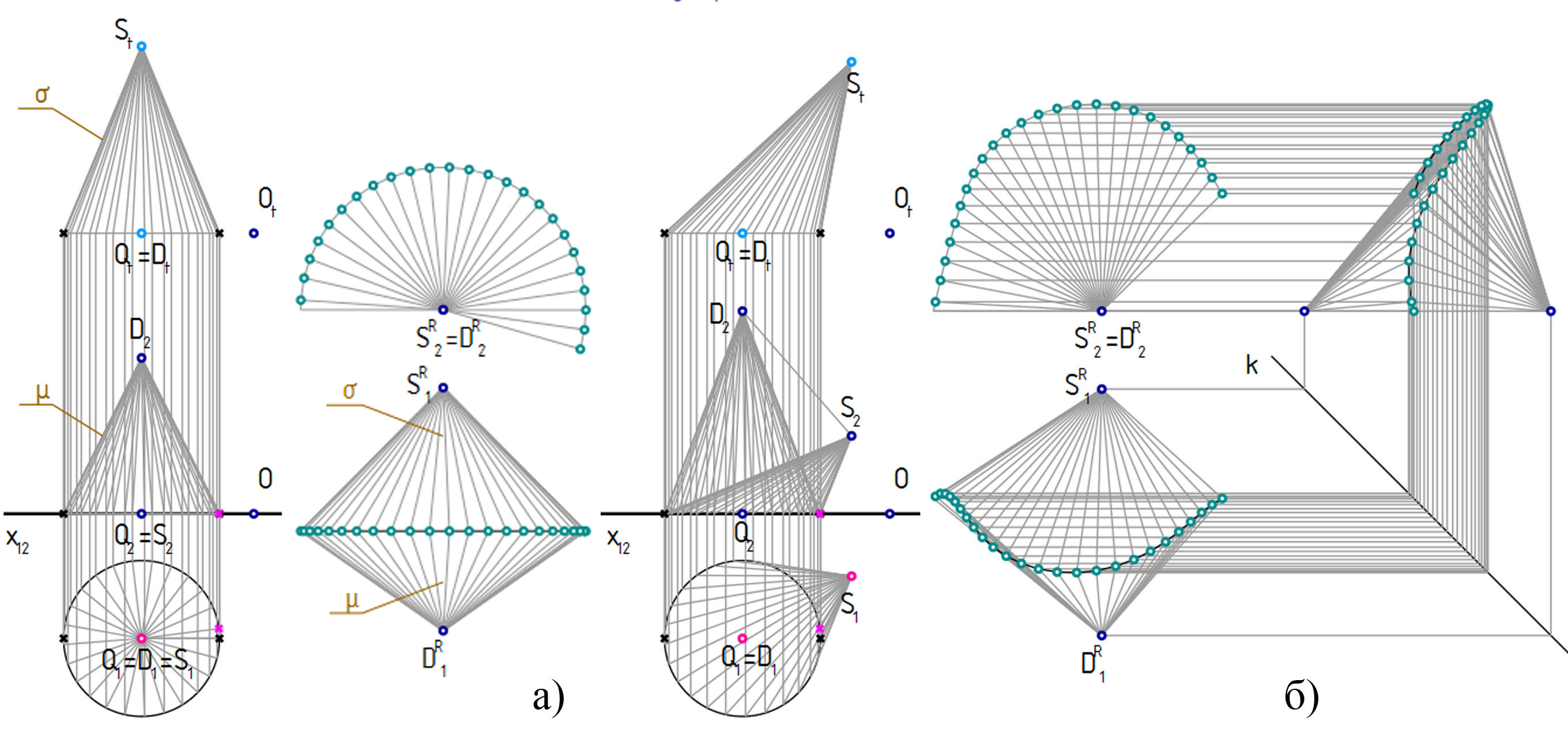
Рис. 6. Развертывание боковой поверхности четырехмерного конуса

Будет своевременно заметить, что студенты при изучении курса начертательной геометрии часто совершают принципиальную ошибку: пытаются использовать пространственное воображение в качестве метода решения задач, пытаются представить модель задачи до ее решения, найти решение, представив его себе, и на этой шаткой основе сформулировать его признаки, в то время как представлять модель задачи следует только когда решение получено. Основной метод решения геометрических задач заключается в знании аксиом и теорем, свойств пространства и моделируемых объектов, в умении абстрактно мыслить и делать логические выводы - все это может поддерживаться наглядностью, но не может быть ею заменено (наоборот, в качестве примера можно привести книгу К.А. Андреева "О геометрических соответствиях в применении к вопросу о построении кривых линий" - без единого рисунка).

Наоборот, легкость решать задачи "ничего не зная" - не зная свойств перпендикулярности, но лишь умея найти геометрическую команду построения перпендикуляра, не чувствуя разницы между пересекающимися прямыми и скрещивающимися, умея проверить решение лишь бесчисленными поворотами трехмерной модели, - таит серьезную опасность: дает ощущение, будто геометрию знать не нужно, так же, как не обязательно уметь считать (есть калькулятор) или писать грамотно (есть Word).

9.

Рассмотренные задачи показывают, что наглядное многомерное моделирование возможно. Простым и удобным инструментом для этого является знакомый по курсу начертательной геометрии и инженерной графики ортогональный чертеж. В частности, в статьях и докладах, посвященных моделированию объектов многомерного пространства, часто используется именно он [7, 18-20].

Для практического применения приемов многомерного моделирования требуется система, дающая возможность создавать и использовать составные построения как последовательности элементарных. Такую возможность, к примеру, дает AutoCAD ([21, 22]), хотя при этом требуется знание языка LISP или VisualBasic и внутренней модели данных системы AutoCAD; такая возможность заложена в систему «Симплекс» ([1, 7]).

Иллюстрации к докладу были подготовлены с использованием разработанного автором интерпретатора графических команд на языке JavaScript, работающего в среде веб-браузеров (в том числе мобильных) для совместного использования с Интернет-системами. Начата работа по созданию для интерпретатора визуального интерфейса на принципах, изложенных в [3].

Основные результаты

Сформулированы критерии наглядности в отношении многомерного геометрического моделирования. Этим критериям удовлетворяют различные способы представления объектов многомерных пространств на плоскости, в частности, ортогональный чертеж (гиперэпюр Радищева). Рассмотрено применение всего комплекса методов исследования многомерных объектов, доступных в трехмерном пространстве и на плоскости, - проецирование, рассечение и развертывание.

Показаны примеры решения задач на построение сечения и развертывания боковой поверхности четырехмерной пирамиды, конической поверхности. Показано, что для упрощения многомерного геометрического моделирования требуются системы, предоставляющие возможность оперировать составными построениями.

Список литературы

1. Волошинов Д.В. Инструмент для геометрического эксперимента. Каким ему быть? [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2015/papers/47/

2. Горнов А.О. К дискуссии о судьбе дисциплины «Начертательная геометрия» [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2011/papers/50/

3. Бойков А.А. О трехмерном моделировании и начертательной геометрии в свете возможностей современных компьютерных систем [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2015/papers/115/

4. Соколова Л.С. Геометрическая подготовка бакалавров в условиях ухода классического чертежа из современного высокотехнологичного производства [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2016/papers/33/

5. Кузнецов Н.А. К вопросу о наглядности изображений // Начертательная геометрия и инженерная графика: сборник науч.-метод.статей. 1973. Вып. 1. С. 24-30

6. Иванов Г. С. Теоретические основы начертательной геометрии / Г. С. Иванов. М.: Машиностроение, 1998. 158 с.

7. Волошинов Д. В. Конструктивное геометрическое моделирование / Д. В. Волошинов. Saarbrucken: Lambert Academic Publishing, 2010. 355 с.

8. Вальков К. И. Лекции по основам геометрического моделирования / К. И. Вальков. Л.: Изд-во Ленингр. ун-та, 1975. 180 с.

9. Труды Московского научно-методического семинара по начертательной геометрии и инженерной графике. М., 1963. 332 с.

10. Методы начертательной геометрии и ее приложения. М., Гостехиздат, 1955. 412 с.

11. Филиппов П.В. Начертательная геометрия многомерного пространства и ее приложения. Л.: Изд-во Ленингр. ун-та, 1979. 280 с.

12. Станков С. С. Способы преобразования гиперэпюра В. П. Радищева // Вопросы начертательной геометрии. Труды ГПИ имени А А. Жданова. 1963. Том XIX. Вып. 4. С. 5-10.

13. Вышнепольский В. И., Сальков Н. А. О значении геометрии в технике и науке [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2017/papers/7/

14. Асекритова С. В., Токарев В. А., Шевелев Ю. П. Компетентностный подход к преподаванию дисциплин начертательная геометрия. инженерная и компьютерная графика[Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2016/papers/55/

15. Курс начертательной геометрии на базе ЭВМ / Тевлин А. М. [и др.]. М.: Высшая школа, 1983. 176 с.

16. Ротков С.И. Разработка методов и средств геометрического моделирования и компьютерной графики пространственных объектов для CALS-технологий. Дис. ... докт. техн. наук: 05.01.01. Нижний Новгород, ННГАСУ, 1999. 280 с.

17. Тюрина В.А. Разработка методов преобразования каркасной модели в задаче синтеза образа 3D объекта по его проекциям. Дис. ... канд. техн. наук: 05.01.01. Нижний Новгород, ННГАСУ, 2003. 170 с.

18. Дмитриева И.М., Иванов Г.С. О профессиональных компетенциях в преподавании начертательной геометрии [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2017/papers/3/

19. Короткий В.А. Геометрическое моделирование поверхности посредством ее отображения на четырехмерное пространство // Омский научный вестник. 2015. № 137. С. 8-12.

20. Глазунов К. О., Лызлов А. Н. Начертательная геометрия пространства-времени [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2014/papers/23/

21. Хейфец А. Л. Геометрическая точность компьютерных алгоритмов конструктивных задач [Электронный ресурс]. Режим доступа: http://dgng.pstu.ru/conf2016/papers/74/

22. Программа для ЭВМ «Построение кривой второго порядка, проходящей через данные точки и касающейся данных прямых» / Короткий В.А.: Свидетельство о государственной регистрации № 2011611961 от 04.03.2011 г.

Головнин Алексей Алексеевич (28 марта 2017 г. 0:48)	Здравствуйте Алексей Александрович! В Вашем докладе Вы вскользь упоминаете «параллельные аксонометрии». Но ведь в учебном курсе НГ такое словосочетание – тавтология. (Аксонометрическая проекция - способ изображения геометрических предметов на чертеже при помощи параллельных проекций). Получается, что студентам мы даем определения, которые не работают в сообществе геометров? Вопрос возможно не к Вам – правильно ли это – в студенческих учебниках излагать знания, звучащие ошибочно в другой ситуации (в научной статье)? Всегда помня о практической направленности нашего предмета (технические науки), сверяю его содержание с нуждами производства. Неоднократно задавал производственникам вопрос, применяете ли Вы где-нибудь аксонометрию? Один раз получил ответ – в электрических шкафах. При комплексном чертеже конструктору при изготовлении первого образца надо было идти в цех и помогать рабочему разбираться в проводах. В случае оформления чертежа в виде аксонометрии, рабочий говорил, что все понятно и отказывался от помощи. Вы решаете вопрос о наглядности в пространстве больше трех. Какова Ваша адресная аудитория кроме геометрического сообщества? Ведь «чертеж – язык техники», должен быть понятным рабочему. Кому нужна наглядность в контексте многомерного моделирования? Каково, на Ваш взгляд соотношение между многомерной геометрией и многофакторным анализом, дифференциальными уравнениями в частных производных, тензорным исчислением и вообще разделами математики, рассматривающим несколько переменных? Я один из тех, о ком Александр Олегович сказал, что ждал Вашего появления. Также, как и Александр Олегович, желаю успехов в долгоожидаемом завершении задуманного. С уважением Головнин А.А.
Селиверстов Александр Владиславович (28 марта 2017 г. 15:10)	Здравствуйте, Алексей Александрович и Алексей Алексеевич! Действительно, если отбросить детали, факторный анализ сводится к использованию проекции на пространство малой размерности, например, на плоскость. Таким образом, эта быстро развивающаяся область математики близка к НГ и может служить для обоснования значимости и современности многомерной НГ. Но часто ли используется на практике гиперэпюр Радищева? Для студентов первого курса это трудно. Хотя может быть очень полезно именно при обсуждении на факультативе. Например, как описал Эдуард Владимирович Козырев: "В так называемом кружке участвуют три -- два человека, обычно по два человека на одну тему. Приглашаются успевающие студенты с обещанием сократить обязательную графическую работу и повышением оценки на зачете." (Комментарий от 22 марта 2017.) С другой стороны, часто приходится иметь дело с большим числом параметров, когда графические методы становятся слишком сложными. Хорошо бы знать пример реального использования гиперэпюра Радищева при решении инженерной задачи методом факторного анализа. Конечно, можно переформулировать известные примеры, используя графические методы. Некоторое обоснование пользы четырёхмерной геометрии предложил Геннадий Сергеевич Иванов (комментарий от 6 марта 2017). Но будет ли такая формулировка понятнее и удобнее? Или это лишь упражнение с заранее известным ответом? В частности, наглядность при обсуждении параметрически заданных пространственных кривых и поверхностей легко достигается анимацией, включая механические модели, которые существовали задолго до появления компьютеров. Кстати, об этом говорит название "кинематические поверхности".  Конечно, можно сказать, что это гиперэпюр Радищева -- это технология двойного назначения. Но как тогда убедить многих студентов (и не только их), что такое назначение действительно существует? И это не насмешка, а серьёзный вопрос. Наконец, благодарю Алексея Александровича за интересные и тщательно написанные доклады. А если бы они были доступны с самого начала конференции, то можно было избежать некоторых разногласий. С уважением, А.В. Селиверстов
Бойков Алексей Александрович (29 марта 2017 г. 1:22)	Здравствуйте, уважаемый Алексей Алексеевич! Спасибо за внимание к дакладу и теплые пожелания. Отвечаю на вопросы: 1. В некоторых трудах я встречал также термин "центральная аксонометрия" в обозначении перспективы. Хотя Вы совершенно правы, не стоит плодить сущностей. На сегодняшний день термин устоялся и параллельная аксонометрия звучит как "масло масляное". Спасибо за замечание. 2. Я стою на позиции, что чертеж - многофункциональный инструмент для решения научных и прикладных задач. В своем докладе Никифоров П.В. "внезапно" показал прикладное значение мнимых точек. Использование 4D для создания технических поверхностей демонстрировалось неоднократно. С другой стороны развертывание четырехмерных поверхностей - это такая "шахматная" задачка, решенная мною в качестве контрпримера к докладу Соколовой Л.С. 3. Самое прямое. Моя дипломная работа в 2004 году была посвящена кластерному анализу многомерных выборок данных. Хотя методы, используемые традиционно в многомерном статистическом анализе, кажется, далеки от НГ, но вот главные компоненты - особым образом построенная косоугольная проекция. с уважением, А.Бойков
Бойков Алексей Александрович (29 марта 2017 г. 1:34)	Здравствуйте, уважаемый Александр Владиславович! Спасибо за внимание к докладам и положительную оценку. К сожалению, раньше "доложиться" не мог. Насчет гиперэпюра - один из вариантов его используется в ключевом методе моделирования отсеков технических поверхностей. Но это не факторный анализ. Навскидку не приведу. Достоинство гиперэпюров, на мой взгляд, заключается в их доступности для понимания. Но это 4-5 измерений, если их 100 - совсем другой случай. Отдльное спасибо за напоминание в Вашем докладе об организации символьных вычислений. Мысль о том, что это практически возможно сейчас при разработке любой системы, не дает мне покоя. с уважением, А.Бойков