ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТОВ ТРЕХМЕРНОГО МОДЕЛИРОВАНИЯ И МЕТОДОВ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ДЛЯ ОПРЕДЕЛЕНИЯ РАССТОЯНИЯ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
English version

|
Карабчевский Виталий Владиславович | (Донецкий национальный технический университет) |
Аннотация
Рассмотрено совместное использование методов начертательной геометрии и инструментов трехмерного геометрического моделирования для определения расстояния между скрещивающимися прямыми. Описаны средства перехода от комплексного чертежа к трехмерной модели. Обосновано применение разработанных методов и средств в учебном процессе.
Ключевые слова: начертательная геометрия, трехмерная модель, расстояние между скрещивающимися прямыми
Известно, что для определения расстояния между скрещивающимися прямыми применяется два основных способа. При общем положении исследуемых прямых, следует построить прямую, проходящую через произвольную точку одной из прямых и параллельную другой прямой. Опустив перпендикуляр из произвольной точки другой прямой на заданную пересекающимися прямыми плоскость и отыскав точку пересечения перпендикуляра с плоскостью, получим отрезок, длина которого и представляет собой искомое расстояние.
Второй способ состоит в приведении одной из прямых в проецирующее положение. В общем случае для этого нужны две замены плоскостей. Тогда расстояние между прямыми будет равно длине перпендикуляра, опущенного из точки, представляющей проекцию такой прямой, на другую прямую.
Первый способ более нагляден, если перейти к трехмерному представлению исследуемых объектов, с его применением была получена иллюстрация, использованная в [1] и некоторых других публикациях, однако в рамках курса «Компьютерная графика» автор требовал от студентов решать задачи с помощью AutoCAD вторым способом, упомянутая иллюстрация показывалась на лекциях с некоторыми пояснениями.
Было принято решение перейти к выполнению работы в трехмерном представлении, как это было сделано для задач на сечение поверхностей и некоторых других метрических задач [2,3,4].
По условию, нужно найти расстояние между скрещивающимися прямыми m и n. Прямые задаются отрезками, координаты концов отрезков содержатся в таблице. На первом этапе студенты выполняют построение, соответствующее левой части рисунка 1. Линии связи между точками должны состоять из двух частей (фронтальной и горизонтальной), чтобы обеспечить возможность перехода к трехмерному представлению. В правой части рисунка построены проекции прямой k, параллельной прямой n и проходящей через произвольную точку прямой m, точку назовем A.
Далее, с помощью команды «Rotate3D» проекции объектов на фронтальную плоскость разворачиваются вокруг оси Х на 90º, разворачиваются и объекты, обозначающие ось Z (рисунок 2).
После этого, нужно построить трехмерные модели прямых m, n и k. Для этого фронтальные части линий связи, заданные отрезками, копируются с переносом одного из концов на горизонтальную плоскость, второй конец будет задавать точку в системе XYZ, заданной на рисунке. Таким образом, будет получена модель, представленная на рисунке 3. Для повышения наглядности изображения куска плоскости, определенной пересекающимися прямыми m и k, построен отрезок, соединяющий концы отрезков, задающих эти прямые. На основе полученного треугольника строится трехмерная грань (с помощью команды «3Dface»), на рисунке 3 она имеет цвет «cyan» и непрозрачна при выбранном визуальном стиле. Построены также линии связи между конечными точками отрезков в трехмерной модели и их фронтальными проекциями. Для решения задачи они не нужны, но для понимания модели обучаемыми, полагаю, полезны.
На рисунке 4 приведены результаты решения задачи. Нужно из произвольной точки прямой n опустить перпендикуляр на плоскость mk. В качестве такой точки используем середину отрезка, задающего n, назовем ее B.
При решении задачи на плоском листе комплексного чертежа для отыскания направления перпендикуляра пришлось бы использовать свойства проекций прямого угла, строить фронталь и горизонталь плоскости, искать точку пересечения перпендикуляра с плоскостью способом сечения, пришлось бы еще определять длину перпендикуляра, заданного проекциями. С использованием трехмерной модели задача решается проще. Следует перейти к системе координат, горизонтальная плоскость которой совпадает с плоскостью mk. Для этого можно использовать команду «UCS» с опцией «3point».
Принимая во внимание, что искомый перпендикуляр будет представлять собой отрезок, начальная точка которого совпадает с точкой В, а конечная имеет координаты x и y, совпадающие с одноименными координатами точки В и координату z, равную 0, применим команду «Line» с координатным фильтром «.xy».
Command: Line Specify first point: <указываем точку В>
Specify next point or [Undo]: .xy
of <указываем точку В> (need z): 0
В результате будет построен отрезок, перпендикулярный плоскости mk, длина которого определяет расстояние между скрещивающимися прямыми. Можно найти и угол скрещения между m и n, он равен углу пересечения между m и k. В ходе решения задачи и по его окончании можно использовать инструмент «3Dorbit», зуммирование и другие видовые операции, что позволяет хорошо представлять положение исследуемых объектов в пространстве и сознательно осваивать изучаемый геометрический алгоритм.
Практика показала, что при решении задачи вышеприведенным способом студенты делают меньше ошибок, чем при решении способом замены плоскостей, а ассистентам легче принимать лабораторные работы.
Таким образом, сделан очередной шаг от курса, который в середине 90 годов прошлого века назывался «Инженерная и компьютерная графика» и по содержанию представлял собой компьютерную начертательную геометрию к курсу с названием «Компьютерная графика», содержание которого может быть характеризовано как решение базовых геометрических задач с применением отдельных методов начертательной геометрии и инструментов трехмерного геометрического моделирования. Разумеется, что этим предметом графическая подготовка студентов направлений 09.03(04).02 («Информационные системы и технологии»), 09.03(04).04 («Программная инженерия») и 02.03(04).01 («Математика и компьютерные науки») не ограничиваются. На старших курсах они осваивают еще несколько предметов, предусматривающих изучение алгоритмов геометрического моделирования, использования и разработки средств компьютерной графики [5].
Возникает вопрос: нужны ли элементы начертательной геометрии в упомянутом курсе? Приведенный пример и задачи, кратко рассмотренные в [2,3,4], показывают их полезность и, в ряде случаев, необходимость. Можно ли применять термин «начертательная геометрия» в тех случаях, когда не применяется ручное черчение? Можно, ведь начертательная геометрия есть наука об изображениях, проекции геометрических моделей на экран компьютера таковыми являются!
Список литературы
Рисунки к докладу
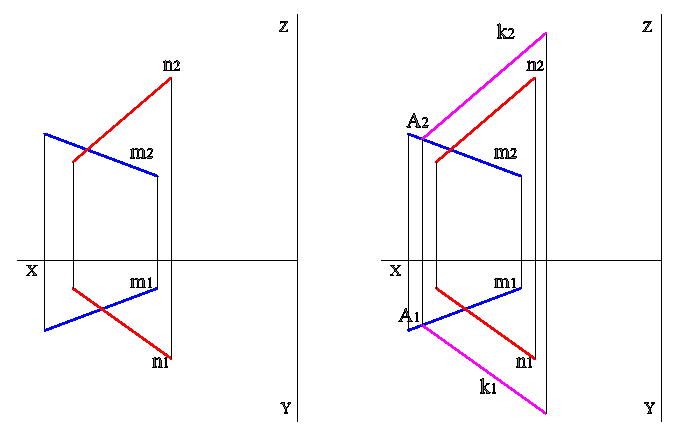
Рис. 1 Построим прямую k
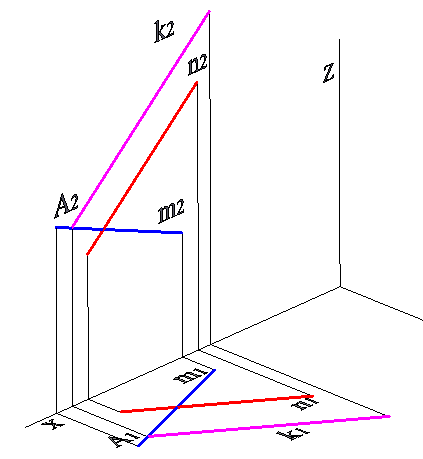
Рис. 2 Поворот вокруг оси x
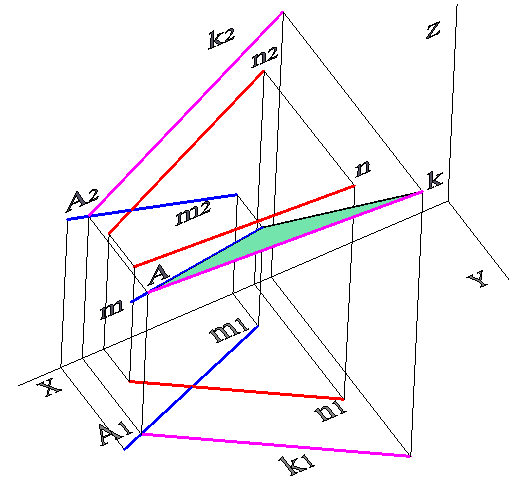
Рис. 3 Трехмерная модель плоскости mk и прямой n
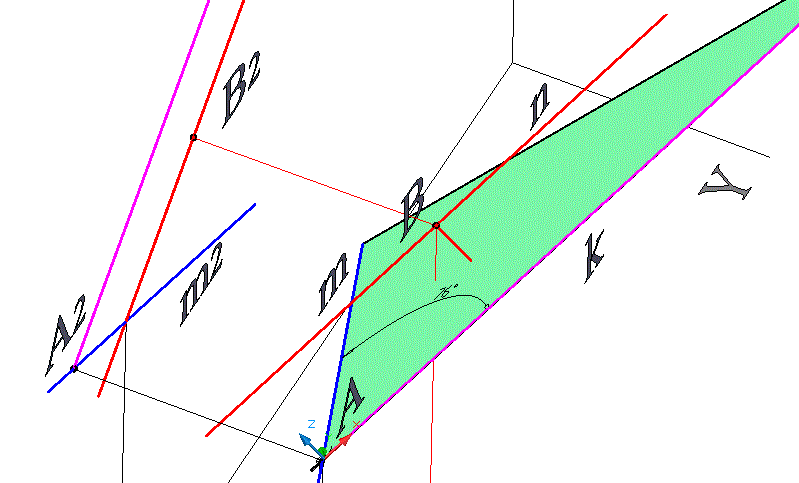
Рис. 4 Перпендикуляр из точки B на плоскость mk
Вопросы и комментарии к выступлению:

Хейфец Александр Львович (18 марта 2019 г. 12:02) |
Виталий Владиславович, приведенные алгоритмы и мы применяем в нашем курсе. Только с Вашими выводами согласиться трудно. Здесь имеют место прямые операции в виртуальном 3d пространстве. НГ здесь нет, ведь ни теорему о прецировании прямого угла, ни двойную замену Вы здесь не применяете. А непосредстванно крутитесь в 3d пространстве. Конечно, если Вы восприятие экрана и окружающего мира рассматриваете как проявление НГ, то возражать Вам бесполезно. Мы постепенно развиваем теоретический курс в SolidWorks'е, в котором есть 3d параметризация. В данном примере достаточно в 3d эскизе построить два отрезка, потроить третий отрезок с коцами на первых двух и придать ему перпендикулярность к каждому из них. Все стало еще проще. Здесь я ожидаю всплеска эмоций оппонентов. Как же, нажал кнопку и все. Но во первых, студенту необходимо знать, что кратчайшее расстояние между скрещивающимися прямыми - это их общий перпендикуляр (геометрия!). Во вторых, налицо еще один пример освобождения от рутинных операции. Необходимо ставить задачи не по нахождению кратчайшего расстояния, а более значимые, где эта опрация - лишь одно из элементарных действий (как провести линию карадашом на бумаге). То есть "поднимать планку". С уважением. А.Л. Хейфец. |

Сальков Николай Андреевич (18 марта 2019 г. 14:58) |
Александр Лвович, пиведенные здесь рисунки представляют собой 2 ортогональных чертежа и 3 аксонометрических. И это Вы считаете не НГ? Странно. Что же тогда это такое? На этот вопрос никто, кроме В.А. Короткого, так и не ответил внятно. Нет конкретных ответов на конкретно поставленные вопросы. Применение компьютера, даже с его кнопочками, как Вы всегда иронизируете, все равно является применением инструмента, пусть и более сложного, чем пресловутый карандаш с циркулем, но инструмента, с помощью которого получают изображение на экране. Или на экране мы получаем не изображение? Тогда что же? А любой инструмент предполагает еще и знание чего-то, кроме как работать с инструментом. И это знание - геометрия, в том числе и начертательная. Виталий Владиславович правильно согласился со мной - НГ есть теория изображений. Да об этом ведь в каждом учебнике по НГ написано на первых же страницах! С уважением, Н.А. Сальков |

Хейфец Александр Львович (18 марта 2019 г. 18:36) |
Николай Андреевич, рисунки, которые Вы упомянули, автор привел лишь для пояснения 3d построений. Построения же выполнены 3d моделированием. Поэтому, Вы сначала разберитесь, затем пишите, а то у Вас получилось наоборот. С уважением. А.Л. Хейфец. |

Головнин Алексей Алексеевич (18 марта 2019 г. 23:04) |
Здравствуйте Виталий Владиславович! Имею свой опыт по использованию компютерной графики, но 2D, для решения задач НГ, а именно – построить третий вид по трем данным. Даже пытался нарабатывать методические приемы. Все равно получается сложнее, чем карандашом на бумаге. Начертательная геометрия – для человека с карандашом и бумагой, но не для компьютера. Представляется, что применение 3D-компьютерной графики в том виде, в котором Вы привели, по крайней мере, не рационально. Требует предварительно хорошего освоения НГ (для иллюстрирующих картинок?), что не плохо, но также и очень хорошего знания КГ, т.е. в завершении курса. Но в этом случае у студента может возникнуть вопрос, а зачем так сложно. Вы предлагаете применить команду «Rotate3D», т.е. как бы 3D задача переводится в плоскость, но потом применяете команду «UCS», т.е. какие-то объекты все же не в плоскости. Но в этом случае неправильно говорить, что Вы использовали НГ. Если не требуется построение общего перпендикуляра, как в условии Вашей задачи, а требуется только найти расстояние между скрещивающимися прямыми, то решение представляется очень перегруженным (ради только того, чтобы сказать, что здесь была НГ?). Представляется, что Ваша задача может быть решена тремя простыми действиями менее чем за одну минуту. 1. Скопировать одну из прямых привязкой ко второй прямой. Получаем плоскость, параллельную прямой. 2. Командой «UCS» вводим пользовательскую систему координат с плоскостью XY на полученной плоскости. 3. Командой «Свойства» определяем координату Z любой точки на исходной прямой, это и есть расстояние между прямыми. Зато предшествовать такому решению будет решение этой задачи в голове студента методами школьной геометрии, что представляется более полезным и лучше развивающим «пространственное мышление» студентов. Еще проще как предложил Александр Львович, решить в программе SolidWorks, в котором есть 3d параметризация, но тоже прежде чем сесть за кнопки, надо найти решение в голове. Программы развиваются и неправильно делать вид, что этого развития нет и что мы используем в 3D-компьютерной графике начертательную геометрию. С уважением Головнин А.А. |

Головнин Алексей Алексеевич (18 марта 2019 г. 23:05) |
третий вид по двум данным |

Сальков Николай Андреевич (19 марта 2019 г. 1:10) |
Александр Львович, и опять Вы ловко ушли от конкретного ответа, обвиняя во всем оппонента: он, дескать, не разобрался! А картинки-то остались! И как быть с ними? Привожу текст доклада: "Далее, с помощью команды «Rotate3D» проекции объектов на фронтальную плоскость разворачиваются вокруг оси Х на 90º, разворачиваются и объекты, обозначающие ось Z (рисунок 2)." Так приведенный рис. 2 - это только для "пояснения", а не то, что получается на самом деле? Ох и любите Вы юлить, Александр Львович! С уважением, Н.А. Сальков |

Карабчевский Виталий Владиславович (20 марта 2019 г. 14:39) |
Здравствуйте, уважаемые коллеги! Согласен с Алексеем Алексеевичем в том, что правая часть рисунка 1 соответствует шагу решения задачи, который можно пропустить и построить прямую k в трехмерной модели, путем копирования n. Но студентам рассказано, как выглядят проекции параллельных прямых, они это используют, но если находится студент, который этот шаг пропустит, т.е. поступит так, как Алексей Алексеевич рекомендовал, это допускается. После выполнения команды UCS расстояние между скрещивающимися прямыми уже найдено, я это так и объясняю. Более того, совпадение координат z начала и конца отрезка прямой n студенты проверяют перед построением перпендикуляра, т.е. проверяют, параллельна ли прямая n плоскости mk. Потом строят перпендикуляр, как описано. Зачем? Чтобы научиться его строить. Ведь одна из первых задач в традиционном курсе начертательной геометрии – опустить перпендикуляр из точки на плоскость. А если применить команду Plan, можно увидеть треугольник в натуральную величину, не нужно его подвергать двум заменам плоскостей или вращать вокруг линии уровня, хотя такие задания я пока тоже даю. Что хочу заметить в отношении «подъема планки». Обучать следует от простого к сложному. Не рассмотреть решение простых геометрических задач в AutoCAD и начать с более мощных средств геометрического моделирования – это все равно, что при обучении программированию пропустить сумму элементов массива, сортировку методом пузырька и прочие классические приемы. По поводу продолжения обучения процитирую: Разумеется, что этим предметом графическая подготовка студентов направлений 09.03(04).02 («Информационные системы и технологии»), 09.03(04).04 («Программная инженерия») и 02.03(04).01 («Математика и компьютерные науки») не ограничиваются. Видно, что готовятся не только пользователи, но и разработчики графических приложений. На третьем курсе у меня разрабатывают графические редакторы (курсовое проектирование), много выпускных работ по этой тематике, в [5] об этом написано подробнее. С уважением, В.В. Карабчевский |

Шахова Алевтина Бруновна (20 марта 2019 г. 23:40) |
Здравствуйте Уважаемые коллеги: Виталий Владиславович, Николай Андреевич, Алексей Алексеевич и Александр Львович, как всегда обсуждаем очевидное, соглашусь с Александром Львовичем, любая САПР содежит команды параллельности, перпендикулярности, равенства, касания и т.д., необходимо только ими воспользоваться. С уважением Шахова А.Б. |

Карабчевский Виталий Владиславович (21 марта 2019 г. 18:53) |
Уважаемая Алевтина Бруновна! Нельзя спорить с тем, что в Solid Works рассмотренную мною задачу можно решить иначе, что может будет и немного проще. Используемая мной методика предназначена для обучения студетов-«айтишников» отдельных направлений и профилей началам компьютерной геометрии, для этого наилучшим образом подходит именно AutoCAD, а содержание заданий состоит в решении базовых геометрических задач как способами начертательной геометрии (и как дань традиции и пользы студентов ради) так и в 3D в AutoCAD. Это происходит на втором или третьем семестре, а потом программисты у меня изучают предмет «Архитектура и проектирование графических систем», где не столько моделируют, сколько программируют, будущие дизайнеры после 3D моделирования в AutoCAD изучают 3D Studio (и не только). Будущие «сапровцы» изучают и Solid Works и CATIA, но на своей выпускающей кафедре, которая просит меня готовить их так, как я изложил. Компьютерных математиков выпускает моя кафедра, для них начать изучение компьютерной графики с элементарных геометрических задач тоже полезно. Разумеется, это мое и некоторых коллег мнение, можно сказать, что все изложенное не приносит никакой пользы. Действительно, даже на нашем факультете компьютерных наук и технологий, я работаю примерно с половиной студентов, а если считать по профилям, то с меньшей частью. Есть кафедры, где обходятся без компьютерной графики, или читают в этом курсе программирование с применением OpenGL. Даже успехи моих студентов (дипломы Всеукраинских конкурсов студенческих научных работ, победы и призовые места на олимпиадах), не являются строгим доказательством целесообразности применения моей методики преподавания. Всегда можно сказать, что достигнутое достигнуто не благодаря а вопреки. Но настаиваю на том, что обучать нужно от простого к сложному. Если не убеждает мой пример с изучением программирования, давайте предположим, что математикам запретили рассказывать о производных и как их брать, а предложили сразу учить использованию MathCAD или подобной системы. |

Карабчевский Виталий Владиславович (21 марта 2019 г. 19:09) |
Здравствуйте, Александр Львович! Я не утверждал, что всякое изображение является проявлением НГ, а только "проекции геометрических моделей на экран компьютера таковыми являются" и, следовало уточнить, геометрических моделей, полученных, хотя-бы отчасти, с применением инструментов НГ". А возражать - всегда полезно, рад услышать любое мнение. С уважением, В.В. Карабчевский |

Сальков Николай Андреевич (21 марта 2019 г. 21:01) |
Виталий Владиславович, это я утверждал, что НГ является теорией изображений (об этом писали многие геометры, я их когда-то перечислял, даже цитировал), а отсюда я также утверждал, что любое изображение есть проявление НГ. Но спорить со мной Александру Львовичу уже надоело, ведь я опираюсь на мнение довольно-таки известных ученых и на очевидные факты, а Александр Львович, не отвечая ни на один конкретно поставленный мною вопрос, только и говорит, что я не знаю КГ. По-моему, это не аргумент в споре - так и я могу. С уважением, Н.А. Сальков |

Карабчевский Виталий Владиславович (23 марта 2019 г. 14:22) |
Здравствуйте, Николай Андреевич! Я согласен с Вашим утверждением отчасти. Если воспользоваться Paint, фотошопом, иллюстратором, то полученные изображения не связаны с НГ ни методами генерации, ни способами визуализации, не будет проявлением НГ и двумерный чертеж в AutoCAD и схема, план и т.п. изображения. А проекция трехмерной модели - несомненно является, если модель получена с применением методов НГ, даже и 2D модель, то тем более. Хотя если считать проявлением НГ биологический "аппарат проецирования", т.е глаз с хрусталиком и сетчаткой, то в этом случае любое изображение есть проявление НГ. С уважением, В.В. Карабчевский |

Сальков Николай Андреевич (23 марта 2019 г. 19:48) |
Здравствуйте, Виталий Владиславович. Конечно же, в рисунках детей из детского сада невозможно разглядеть НГ, однако, если внимтельно почитать книжку авторов: Фролов С.А., Покровская М.В. В поисках начала: Рассказы о начертательной геометрии. - Минск, Вышэйшая школа, 1985. - 189 с., то возникает совершенно другое представление о роли и месте НГ в теории изображений вообще, и в изображениях, выполненных с ичпользованием информационныз технологий в частности. Здесь, на этом форуме, многие верят высказываниям С.А. Фролова. Ну а насчет чертежа - тут с Вами и А.Л. Хейфец поспорит, ведь он постоянно уличает НГ исключительно в пособничестве черчению. НГ не только является проявлением "биологического аппарата проецирования": вспомните фотокамеру, в том числе и цифровую, киноаппараты различного вида, кинопроекторы... Я уже писал, что НГ - теория отображения пространства одного измерения на пространство другого, а не просто фотка на плоскости. ОТОБРАЖЕНИЕ! И художники, и скульпторы отображают действительность трехмерного мира - одни на холсте, то бишь, плоскости, другие - в терхмерном виде - в Вашем 3D! Это лишь сотая часть того, что дает НГ. Не стоит ее рассматривать так узко! И то, что НГ является проявлением любого изображения - это не я сказал. Это сказал академик Н.Ф. Чеверухин, а я только повторил. Будем спорить с академиком? Ну-ну... С уважением, Н.А. Сальков |

Горнов Александр Олегович (23 марта 2019 г. 20:42) |
Николай Андреевич, хочется уточнить, что сказал Н.Ф.Черверухин : "НГ является проявлением любого изображения " или "Любое изображение является проявлением НГ " . А.О. |

Сальков Николай Андреевич (23 марта 2019 г. 21:38) |
Александр Олегович, это я где-то вычитал, но не помню где, давно это было, так что не могу утверждать о точности цитаты. Но смысл понятен. |

Горнов Александр Олегович (23 марта 2019 г. 22:08) |
Николай Андреевич , тогда, имея в виду Ваше от 21;38, мягко говоря , "не хорошо .".. присваивать академику Ваши не очень корректные соображения. Смотрите , Вы даже сами им не следуете . Если даже не трактовать Вас буквально, а категоричность заявление это позволяет, то любое изображение - в том числе и детей в детском саду ( чем не одно из любых? ) , все таки проявление НГ. ?! Кстати, поскольку они плоские, то ассоциировать их с проекциями и "разглядеть НГ" гораздо проще и естественнее, чем многие во многих другиж изображениях . А.О, ... |

Сальков Николай Андреевич (23 марта 2019 г. 22:40) |
Александр Олегович, видимо, я резко впал в идиотизм, потому что совершенно не понял, о чем Вы только что написали. Единственное, что понятно - это Вы очень сердиты тем, что я, дескать, приписываю академику именно свои, а не его высказывания. Повторяю еще раз: эта фраза у меня в памяти связана именно с Четверухиным, но я не желаю положить жизнь, выискивая во всех доступных источниках доказательство этому. И еще. Если Вы разъясните, чем так уж коренным образом отличаются фразы, которые Вы привели в 20:42, которые, по-моему, являются проявлением дуализма, коим так богата геометрия, буду признателен, поскольку эти две фразы - это одно и то же. Н.А. ... |

Горнов Александр Олегович (24 марта 2019 г. 8:34) |
Николай Андреевич, с чем я согласен , так это то, что не хочеться тратиться, на мой взгляд, на бесперспективный обмен мнениями. Как говорят:" : " Замнем для ясности ." А.О. |

Наместников Алексей Юрьевич (24 марта 2019 г. 12:27) |
Николай Андреевич, 21 марта споткнулся о Ваши фразы «я утверждал, что НГ является теорией изображений» и «я также утверждал, что любое изображение есть проявление НГ». Сверился с уважаемыми А.Климухиным и С.Ожегововым — исполнил изображение (без НГ, карандаша, ножниц и клея, в Фотошопе): С уважением к Вашим поискам истины, выпускник архитектурного института САИ, победитель институтской олимпиады по НГ в 1970 (заработал «автомат») Алексей Ю. Наместников. PS Самое главное, надо КАЖДОМУ первокурснику объяснить условное пространство эпюра — вся остальная НГ ничуть не сложна, всю можно освоить самостоятельно, даже отражение с тенями в перспективе с тремя точками схода. |

Головнин Алексей Алексеевич (24 марта 2019 г. 12:33) |
Здравствуйте Николай Андреевич! Зная Вас много лет по многим научным трудам и в личном общении как позитивного, искреннего, преданного науке ученого, всегда с вниманием читаю Ваши выступления. Кроме того Вы вместе с Вашим непримиримым визави Александром Львовичем несколько раз подавали, по крайней мере мне лично, пример как надо вести непримиримый спор. Разрешите вслед за Алекеем Юрьевичем поддержать Вас в Вашей активности. Вместе с тем с тем есть и возражения. При ссылке на авторитет академика Н.Ф. Четверухина у меня лично возникает ответ, что с академиком Четверухиным ни спорят, его изучают. Но возникает и возражение о допустимости таких доводов. Это описано, как «аргумент к авторитету» https://studopedia.ru/7_2868_dopustimie-i-nedopustimie-priemi-vedeniya-spora.html Вы также, на мой взгляд, несколько раз использовали такой прием, как «возложение бремени доказательства на оппонента» (там же). Против этого приема лично я ничего не имею, полезный опыт в попытках сформулировать мысли. Но не всем приятно, когда его пытаются принудить аргументировать или опровергать чей-то тезис. По приведенной ссылке можно посмотреть еще много недопустимых приемов в споре. Есть и личный опыт, без этого, наверное, не прожить. Появилось что-то вроде чутья, а в некоторых случаях и аллергия на такие приемы. Предложение – не применять к обсуждению докладов слова «спор». Передача передового опыта, обмен мнениями. (Кстати в части передового опыта есть ощущение, что на этой конференции произошел прорыв в освещении применения 3D-моделирования в учебном процессе.) Желающие задают уточняющие вопросы, высказываются о своем видении по доложенному вопросу. В завершении можно поблагодарить докладчика, или участника обсуждения, если он смог добавить в здание твоих знаний еще один кирпичик. Если кому-то «надоело», можно просто не мешать участникам. В крайнем случае, аргументировано показать ошибки и заблуждения. Ведь это, кроме всего и большая подвижническая работа, которая нигде не записывается. С уважением Головнин А.А. |

Сальков Николай Андреевич (24 марта 2019 г. 14:03) |
Уважаемый Алексей Юрьевич, а не надо спотыкаться! Снова, теперь с доказательствами: "Начертательную геометрию называют также теорией изображений" [Пеклич В.А. Начертательная геометрия. - М.: Изд-во Ассоциации строительных вузов, 2007.- 272 с., Стр. 3]; "Начертательная геометрия - раздел геометрии, в котором изучаются различные методы изображения пространственных форм на плоскости" [Короев Ю.И. Начертательная геометрия. - М.: Кнорус, 2011, С.9]. То же самое пишет Гордон В.О. и Семенцов-Огиевский М.А.: "Предметом НГ является изложение и обоснование способов построения изображений пространственных форм..." [Начертательная геометрия. - М.: Наука, 1977. - С.9]. Мне дальше проводить лиебез или хватит? Любой учебник по НГ для первокурсника содержит в том или ином виде уже выложенные фразы. Так что, уважаемый Алексей Алексеевич, я, как видите, теперь ссылаюсь на многие авторитеты! Все 5 картинок, представленных Вами, Алексей Юрьевич, - это изображения или нет? Если нет, то тогда что же это такое? Никто так и не сумел ответить на этот вопрос - я постоянно на это ссылаюсь и постоянно не получаю внятного ответа. Еще раз: НГ - это отображение пространства одного измерения на пространство другого измерения. Что тут неясого? В результате получаем изображение - на двумерном носителе так называемую 2D, в трехмерном носителе - 3D. Я не был победителем институтской олимпиады, Алексей Юрьевич, но в течение 5 лет, проведенных в институте, ежегодно выступал на конференциях с докладами по различным вопросам НГ. Это для Вас достаточный аргумент? Каждому первокурснику, Алексей Юрьевич, ничего объяснить никто не в силах: нет у нас 68-ми часов в сутках, режут часы у технических предметов, да и студенты бывают не вполне себе восприимчивыми к наукам. С уважением, Н.А. Сальков |

Головнин Алексей Алексеевич (24 марта 2019 г. 14:25) |
Николай Андреевич! А все же, подписи Алексея Юрьевича под изображениями на Ваш взгляд, правильные или нет? Если ошибочны, то в чем? Определения авторитетов, приведенные вами работают в контнксте. Без него они выглядят несовершенными. С уважением Головнин Алексей Алексеевич |

Карабчевский Виталий Владиславович (24 марта 2019 г. 16:22) |
Добрый день, Николай Андреевич! Считаю уместным разделить "проявление НГ" и "применение НГ". В этом случае трехмерная модель (полученная средствами КГ без применения НГ, пример А.Ю. Наместникова) - проявление, т.к. все системы 3D моделирования основаны на методах и алгоритмах, разработанных на фундаменте НГ. При моделировании обычно используется параллельное проецирование на один или несколько видовых экранов, но ведь глаз видит не так - опять проявление НГ или уже применение? Если использованы способы НГ - применение несомненно. Но мой доклад на этой и на прошлой конференциях ставит вопрос о применении элементов НГ в курсе КГ и о применении КГдля изучения методов НГ, хотелось бы знать Ваше мнение по этому вопросу. Уточню, откуда у меня такая методика, для этого, по примеру коллег, обращусь к студенческим воспоминаниям. Я учился в ДПИ на специальности "Прикладная математика", на первом курсе нам читали НГ, меня чудом допустили к экзамену, т.к. мои эпюры ассистенты не принимали - "неряшливо". Одна однокурсница сжалилась и помогла, при этом я заметил, что она не предсталяет картину в пространстве, просто хорошо чертит. На экзамен ассистенты "рекомендовали" оценки (лектор практических занятий не вел), ей 5 мне 3, получили наоборот, как бедняжка плакала! С уважением, В.В. Карабчевский |

Сальков Николай Андреевич (24 марта 2019 г. 19:42) |
Алексей Алексеевич, добрый день! Я не могу перепечатывать весь учебник, чтобы показать, что пресловутый "контекст" напрямую относится к НГ. Тем более, что Пеклич в этом месте поставил точку. Насчет подписей под рисунками. Во-первых, 2, 3 и 4 рисунки являются фотографиями, а это чистая НГ - перспектива, то есть, перспективное изображение на матрицу фотоаппарата. Если же вдаваться в подробности по поводу картинки №2, то (см. мой доклад на этом форуме) художники в обязательном порядке 2 года (!) изучают перспективу. Спрашивается - и зачем же? Чтобы не соблюдать законы НГ??? Что касается первой картинки, то это чистая геометрия, а не "условный язык". Это - графическая модель пространства. Изображение геом. фигур на двух плоскостях проекций. Такие изображения могут быть и не в проекционной связи, например в строительстве часто (в альбомах типовых зданий) план, фасад и разрезы находятся вообще на разных листах. По поводу рисунка №4. Это, по-моему, антиискусство. Искусство должно учить великому и прекрасному, как это ни банально сейчас звучит. Если же такой "художник" именно таким образом напишет Ваш портрет, то, мне кажется, его нельзя будет показывать никому из Ваших знакомых. Теперь о последнем рисунке. Ознакомьтесь, пожалуйста с моим докладом на этой конференции по поводу КГ. Мне не хочется все пересказывать еще и еще. Тем более, что в ГиГ есть статья на этот счет. С уважением, Н.А. Сальков |

Сальков Николай Андреевич (24 марта 2019 г. 20:02) |
Виталий Владиславович, добрый день! Применение и проявление - это термины из одного, так сказать, "блюда". Например, возьмем фотоаппарат. Каждый снимок - это проявление перспективы, мы ее не используем напрямую, ручками, однако же - используем, как-бы "втемную". Не каждый фотографирующий мальчик или девочка знают о перспективе, однако ее иногда неплохо используют. Так и в компьютере. Насчет глаза. В уже упомянутом учебнике Гордона (в ранних вариантах) было написано, что проекции можно получить не только на плоскость, но и на жругие поверхности: на цилиндр, и на сферу. Ну что ж, мне жаль Вашу однокурсницу, однако оценки ставят, в основном, за знания, а не за красивость. Например, так делаю я. Потому что соображать в науках дано, может быть, и не таким уж аккуратистам, а вот впоследствие научить их "делать красиво" можно: со временем научатся, когда очень нужно будет. По поводу Вашего вопроса о применении КГ в НГ. Я провел эксперимент, оказалось, что студенты, не знающие геометрии, в КГ делали постоянные, можно сказать даже дикие, ошибки. Те же студенты (именно те же) после того, как ознакомились предварительно с геометрией, выполняли в КГ работы быстро и без ошибок. Вывод: сначала требуется выучить геометрическую теорию, а затем уж приступать к КГ. С уважением, Н.А. Сальков |

Головнин Алексей Алексеевич (24 марта 2019 г. 23:26) |
Здравствуйте Николай Андреевич! Спасибо за ответ, он меня не устроил, я тоже не ставлю задачу переубедить Вас. Исключительно в порядке обмена мнениями: 1. Я как раз и хотел сказать, что определение должно работать без контекста, а Вы говорите о перепечатке всего учебника, чтобы понятно было о чем речь. 2. По поводу работы НГ в фотоаппарате. Первый телескоп-рефрактор был сконструирован Галилеем в 1609 году, задолго до появления Начертательной геометрии Монжа. Вы возразите, что она работала и раньше. Но почему же тогда фотоаппарат изучают в школе в курсе Физики, а не в курсе НГ в вузах 3. По первой картинке вроде было все предельно ясно, там есть НГ, но Вы - то говорите, что это «чистая геометрия», то «изображение на двух плоскостях», то есть совсем запутали вопрос. 4. По рисунку № 4 Вы грубо подменили тезис, сведя вопрос о НГ к оценке художественной ценности, этот прием описан в моей ссылке как «Подмена тезиса». 5. Вы отослали меня к Вашим трудам, но не дали ссылку, тем более даже номера журнала Г и Г. Я должен их все перечитать? Фактически Вы не стали отвечать, но предлагаете «Ознакомьтесь, пожалуйста с моим докладом». Я бы и ознакомился, но не знаю, что я там должен найти. С учетом первых четырех пунктов, скорее всего, там ответа нет. Когда Вы несколько лет назад пытали меня о том, по каким алгоритмам работает компьютер, я не отправлял Вас к моей статье, «Что там за кнопками», а терпеливо пытался найти новые логические ходы, чтобы Вам было понятнее. С уважением Головнин А.А. |

Сальков Николай Андреевич (25 марта 2019 г. 2:58) |
Алексей Алексеевич, я устал от казуистики! Ну хорошо, отвечу и в этот раз. 1. О нежелании дальнейшего цитирования учебника я отказался именно оттого, что именно Вы заявили, что все цитаты надо рассматривать не в отрыве от всего остального текста, а в контексте. Или это не Вы заявили? Цитирую: "Определения авторитетов, приведенные вами работают в контнксте" (орфографию и пунктуацию я не менял, чтобы меня не обвинили еще в чем-то). Я намекнул в ответ, что хоть в отрыве, хоть с остальным текстом - дело не в этом, а в том, что никакого контекста в данном случае нет и в помине! Фразы сами по себе самостоятельны. Теперь понятно? 2. Перспективу начали серьезно изучать в средние века, до Монжа. И именно перспектива является одним из разделов НГ - ну чего тут непонятного, а??? А физика-то тут причем? Школьники изучают оптику, а не НГ, повторяю - ОПТИКУ!!! Хотя оптика и взаимодействует очень тесно с геометрией. Тут-то что непонятно? 3. Алексей Алексеевич, путаник - это Вы! Нарисуйте, пожалуйста, прямоугольный треугольник. Нарисовали? Это у Вас геометрия или изображение треугольника??? При этом мне нужен ответ такой: или то, или это! Не можете найти ответ? Ну, когда найдете, тогда и я отвечу. 4. Какая "подмена тезиса"? Перекреститесь! Где Вы видите здесь тезис? "Изображение на условном языке кубизм" под картинкой - это Вы считаете "тезисом"? Так я о кубизме и дал свою характеристику, как Вы и просили. Чем мое восприятие этого изображения Вам так не понравилось? Определитесь, наконец, со своими претензиями конкретно, а не пытайтесь уличить мои ответы в чем-то неприличном. Или мне придется поступать также, постоянно привлекая https://studopedia.ru/7_2868_dopustimie-i-nedopustimie-priemi-vedeniya-spora.html. 5. По этому пункту цитирую себя: "Ознакомьтесь, пожалуйста с моим докладом на этой конференции по поводу КГ". У меня такой доклад единственный. Вам лень глянуть? Если не знаете, что там и даже не пожелали просто открыть страничку, ну что-ж, Бог с Вами. Значит, для ожесточенного спора со мной Вам это не нужно. Получается, что Вам не надо знать конкретику, главное зацепиться за что-то и долбить в одну точку! Мне Вам больше сказать нечего. Хотите ссылку? Да на здоровье! Видимо, Вам неохота просмотреть два моих доклада. И все-таки, вот они: http://dgng.pstu.ru/conf2019/papers/2/ http://dgng.pstu.ru/conf2019/papers/48/ Кстати, Вы злостно применили недопустимый прием спора, означенный как "Засыпка вопросами". Пока что с уважением, Н.А. Сальков |

Головнин Алексей Алексеевич (25 марта 2019 г. 7:31) |
Николай Андреевич! Я насчитал у себя один вопрос, которым я вас "злостно засыпал". Ещё один можно было бы поставить после упоминания школьной физики. И то в первом предложении я оговорился, что просто в порядке ознакомления с моим мнением, если конечно оно Вас заинтересует. Я совсем не хотел Вас напрягать ответом. Я понял, что лучше будет согласиться, что НГ везде. Ещё правильнее было бы послушаться Евгения Владимировича и "прекратить" вместо того чтобы обижаться. Я не шучу. Диалектика. С уважением Головнин Алексей Алексеевич
|

Головнин Алексей Алексеевич (25 марта 2019 г. 10:44) |
Николай Андреевич! Неумолимо приближается время завершения нашего общения. Начались главные вопросы, которыми засыпали уважаемого Геннадия Сергеевича. У меня тоже есть важный для меня вопрос. Можно я задам его Вам. Кто и когда назвал теорему Польке основной теоремой аксонометрии. Ведь не думал же Польке, р том, что это основеая теорема, когда её доказывал. Вообще, когда был введен термин аксонометрия. С уважением Головнин Алексей Алексеевич |

Сальков Николай Андреевич (25 марта 2019 г. 14:15) |
Алексей Алексеевич! Я не историк, поэтому заявлять, когда конкретно в каком году и месяце эта теорема была названа впервые основной для аксонометрии, не буду. Единственное, что могу сказать, опираясь опять же на авторитеты (чего Вы не приемлете почему-то), это книга Глазунов Е.А., Четверцхин Н.Н. Аксонометрия. - М.:1953, - С. 32, второй абзац снизу. А вообще с этим вопросом лучше обратиться к Александру Олеговичу Горнову. Он должен это знать. С уважением, Н.А. Сальков |

Карабчевский Виталий Владиславович (25 марта 2019 г. 16:06) |
Здравствуйте, Николай Андреевич! Я также проводил подобный опыт в середине 90 годов прошлого века и пришел к тем же результатам, поэтому оставил начертательную геометрию в курсе инженерная и компьютерная графика, не выбросил ее и тогда, когда он стал называться компьютерная графика. Из Ваших слов можно сделать вывод, что Вы не одобряете мой опыт, уточню свою позицию: без НГ в КГ неуютно, тут мы с Вами союзники, без применения КГ изучать НГ ненаглядно (однокурсница не одна такая была), изучать нужно совместно. При этом не следует бояться КГ, студенты самостоятельно осваивают AutoCAD в нужном объеме, провожу только несколько коротких мастер-классов на лекциях. После такого курса КГ студенты хорошо ориентируются в пространстве, владеют основами AutoCAD, можно на старших курсах писать программы и в среде AutoCAD и с использованием других средств, изучать алгоритмы и разнообразные инструменты геометрического моделирования. Подробнее об этом было в докладе на прошлой конференции и в Дивноморском, в Украине было много публикаций. Проявление и применение можно сравнить с пирожком, где начинка – применение, блюдо одно, но иногда нужно различать его части. По поводу глаза я имел в виду, что глаз осуществляет центральное проецирования на сетчатку, а в КГ может использоваться параллельное проецирование. А проецирование на цилиндр и сферу используется в дизайне, имею интересный опыт. С уважением, В.В. Карабчевский |

Сальков Николай Андреевич (25 марта 2019 г. 19:21) |
Виталий Владиславович, здравствуйте! Я ни в коем случае не против Вашего опыта изучать НГ с помощью КГ. Удачных возможностей в применении! Пирожок? Когда кто-то из знакомых предлагает взять пирожок, неизвестно, что там внутри. Только после пробы начинка проявляет себя. Тот же, кто пирожок печет, начинку применяет. Дуализм... С уважением, Н.А. сальков |

Наместников Алексей Юрьевич (26 марта 2019 г. 11:49) |
Коллеги! Как здорово, что начальство позволило, организаторы КГП-2019 смогли и компьютерные технологии помогли нам пообщаться по важным для каждого и всех вопросам! Главный наш вопрос: ЧТО ДЕЛАТЬ, если урезають? — надо решать по законам развития (Гегелем открытым): - отрицание отрицания (римляне умножали многозначные числа не арабским столбиком — у кого из нас такие способности?); - переход количества в качество (больше полезных для жизни идей!); - единство и борьба противоположностей (не бодаться, а сопоставлять тезисы и антитезисы). Николай Андреевич, благодарен Вам за то, что подтолкнули меня к ценному для меня понятию: НГ ничего не изображает, но точно и достоверно отображает морфологические характеристики 3d-объекта на 2d-проекциях и на особом языке. Разные характеристики на разных проекциях. Нужную проекцию можно раскрасить, сделать наглядной. Как умел Гонзага (привожу не для осведомления Вас, а для красоты беседы): Уверен, теперь мои вечерники не будут на ортогонали изображать перспективную глубину, дескать, «я так вижу». Снимаю шляпу перед Вами, автором морфологического решения колосников для грохота липких пород! Ведь это же 4d-объект!!! И отображения форм, расположений и взаимодействий элементов устройства на плоских чертежах достоверные, понятные! Правда, моя дочь, филолог 40+, почему-то ничего интересного не видит в ваших изображениях: «Справа геометрические фигуры, слева они же в разрезе, а в середине вверху вообще что-то другое». Николай Андреевич, можно ли скруглить ребро-скребок, чтобы меньше снашивалось, дольше служило? Нельзя ли это применить в насосе с четырьмя такими цилиндрами? Всем спасибо, до свидания! Иду учить тому, за что платят — каллиграфии в Художественном училище. |
Назад Go Back
