КРИВЫЕ ВТОРОГО ПОРЯДКА В МОДЕЛИРОВАНИИ ПОВЕРХНОСТЕЙ

Рассмотрены алгоритмы моделирования криволинейных поверхностей, опирающихся на трехзвенные или четырехзвенные замкнутые контуры. Для формообразования применяются сегменты конических сечений. Показана возможность моделирования поверхности способом повышения размерности объемлющего пространства. Предложена методика формирования поверхности с помощью кривых второго порядка и направляющих линейчатых поверхностей. Получены уравнения поверхности, натянутой на плоский треугольный или четырехугольный контур.

Свойства поверхности во многом определяются свойствами линий, образующих эту поверхность. Свойства линий, в свою очередь, определяются видом математических функций, описывающих эти линии. Например, при проектировании динамических обводов из множества алгебраических кривых выбирают циркулярные кривые, а среди циркулярных кривых отдают предпочтение циркулярным рациональным кривым, как обладающим наилучшими динамическими свойствами (Г.С. Иванов).

В современных САПР основным инструментом моделирования кривых линий сложной формы являются NURBS-кривые, благодаря как их свойствам, так и внедрению в международные стандарты CAD/CAM. При этом моделирование поверхности по существу сводится к ее аппроксимации по заданному заказчиком набору координат реперных точек, исходя из заданного порядка гладкости сшиваемой поверхности. Кривая второго порядка в графических САПР представлена как частный случай рационально параметризованной кубической кривой. При этом отсутствует возможность применения кривой второго порядка в качестве базового формообразующего элемента.

Не противопоставляя методы начертательной и вычислительной геометрии и не пытаясь конкурировать с идеологией CALS, рассмотрим примеры кинематического формирования поверхностей с использованием конических сечений. В рассматриваемых примерах используется программное средство построения сегмента конического сечения, заданного своими точками и касательными [1].

Пример 1. Одним из способов моделирования поверхностей является ключевой способ, в соответствии с которым определитель поверхности содержит некоторое геометрическое условие (ключ), посредством которого задается закон изменения формы образующей. Ключ проекционно связан с главными видами, что позволяет рассматривать чертеж с изображением ключа как чертеж двумерной поверхности, находящейся в четырехмерном пространстве.

Обобщенная трактовка всех ключевых способов формирования поверхности как задачи начертательной геометрии четырехмерного пространства дана в [2]. Пусть требуется смоделировать поверхность, свободно натягиваемую на треугольный контур, ограниченный кривыми второго порядка (модель паруса, рис. 1, а). Присваивая узлам произвольные значения координат по оси t, получаем контур ABC в E4. При определенном выборе базисных инциденций плоскости звеньев AC, BC и сами звенья проецируются на xyt прямыми AC и BC, а проекция звена AB определяется из условия его принадлежности плоскости tau [3].

Формируем в E4 два пучка вспомогательных плоскостей. Будем полагать, что плоскости пучка omega с осью CZ перспективны ряду точек звена AB, то есть в этом пучке плоскости пробегают точечный ряд AB от положения 0 до BC. Плоскости пучка delta проходят через базисную точку X и через точки пересечения противолежащих звеньев AC и BC вспомогательными гиперплоскостями уровня y=const. Двупараметрическое множество точек пересечения плоскостей пучков delta и omega образует поверхность, натянутую на контур ABC в пространстве E4, проекция которой на Г(xyz) есть искомая поверхность, а на Г(xyt) - отсек конической поверхности с вершиной C и направляющей AB.

В частности, если одна из сторон контура ABC - прямая линия, а две стороны - конические сегменты, то оба семейства образующих поверхности - кривые второго порядка. Оба семейства образующих - гладкие кривые, следовательно, получаем гладкую поверхность, в каждой своей точке имеющую единственную касательную плоскость.

Поверхность на четырехугольном контуре (фрагмент бортовой обшивки лодки от киля AD до палубной линии BC, рис. 1, в) также моделируется способом выхода в четырехмерное пространство. Выносим контур в E4, придав узлам произвольные значения координат по оси t. Выбираем базисные точки. Устанавливаем соответствие между точками звеньев AB и CD посредством вспомогательных гиперплоскостей уровня x=const, а соответствие между звеньями BC и AD - с помощью гиперплоскостей y=const. Пара соответственных точек, бегущих по звеньям AB и CD, совместно с базисной точкой определяет пучок плоскостей, пробегающих от плоскости палубы до киля. Аналогично, множество пар соответственных точек и базисная точка Z определяют пучок плоскостей omega, пробегающих между шпангоутами AB и CD. Множество точек пересечения плоскостей пучков delta и omega определяет в E4 искомую поверхность, проекция которой на Г(xyt) - коноид с плоскостью параллелизма xt и направляющей коникой. В подпространстве Г(xyt) плоскость delta пересекается с коноидом по кривой второго порядка. Точечные поля delta и delta штрих, вложенные в гиперплоскости проекций Г(xyt) и Г(xyz), связаны на гиперэпюре перспективно-аффинным соответствием, поэтому в исходном пространстве xyz кривая MN также будет участком коники. Множество плоскостей пучка delta индуцирует множество продольных образующих (кривых второго порядка MN) моделируемого отсека поверхности.

Таким образом, если палубная линия BC - участок коники, то, независимо от формы шпангоутов AB и CD, отсек ABCD конструируемой поверхности может быть образован движением дуги кривой второго порядка MN по направляющим AB, CD. При этом форма образующей MN меняется от палубной линии BC до прямолинейного киля AD. Гладкость (дифференцируемость в любой точке) полученной поверхности также доказывается рассмотрением гладкости двух трансверсальных семейств образующих. Сечение MN коноида ABCD, являющегося проекцией поверхности на гиперплоскость xyt, плоскостью delta - алгебраическая кривая 4 порядка. Кривой MN родственно (перспективно-аффинно) соответствует кривая MN на гиперплоскости xyz (см. рис. 1, в). Следовательно, кривая MN - гладкая алгебраическая кривая 4 порядка. Гладкость (отсутствие изломов) произвольной образующей другого семейства доказывается с использованием третьей проекции конструируемой поверхности на гиперплоскость yzt - коноида, в сечении которого плоскостями, параллельными zt, также получаем кривые четвертого порядка.

Семейству сечений zt коноида в пространстве yzt родственно соответствуют образующие в пространстве xyz, заполняющие поверхность между шпангоутами AB и CD (третья проекция фрагмента бортовой обшивки ABCD на рис. 1 условно не показана). Наличие двух семейств гладких образующих на поверхности доказывает ее гладкость (отсутствие изломов). Действительно, наличие излома на поверхности непременно приводит к наличию излома образующих. Но образующие не имеют изломов, следовательно, поверхность в целом также не содержит изломов.

Поверхность в четырехмерном пространстве формируется как двупараметрическое множество точек пересечения двух пучков плоскостей с базисными точками U и V. Нарушение гладкости такой поверхности может происходить только в отдельных (особых) точках. В частности, если какая-либо плоскость пучка U проходит через базисную точку V другого пучка, то получаем, что все плоскости пучка U пересекаются с этой плоскостью в точке V, которая становится особой точкой поверхности. Если точка V несобственная, получаем разрыв непрерывности второго рода.

Пример 2. Пусть дан прямоугольный в плане пространственный замкнутый контур ABCD, фронтальные звенья AB и CD которого - дуги кривых второго порядка, а боковые звенья AD и BC произвольные гладкие кривые (рис. 2, а). Требуется построить непрерывную гладкую (не имеющую изломов) поверхность, проходящую через данный замкнутый контур.

В этом примере использован кинематический способ формирования поверхности: образующая k2 скользит по направляющим AD и BC, плавно изменяя свою форму от дуги конического сечения AB до дуги CD. Ряд последовательных положений образующей формирует конструируемую поверхность. Потребуем, чтобы образующая k2 во всех своих положениях была кривой второго порядка.

Кривая второго порядка на плоскости обладает пятью степенями свободы. Для ее однозначного определения требуется зафиксировать пять элементов (точек и касательных, инцидентных данной кривой), поэтому для управления формой образующей k2 следует указать пять условий, определяющих положение этих элементов (точек и касательных) в зависимости от некоторого параметра u. Конструируемая поверхность имеет прямоугольное в плане основание, ориентированное по осям x и y декартовой системы координат, поэтому в качестве параметра u может быть принята координата y.

Каждому значению параметра u=y должна соответствовать единственная образующая UV=k2, лежащая в плоскости, параллельной фронтальной плоскости xz (см. рис. 2, а). Форма образующей зависит от параметра u следующим образом. Данному значению параметра u=y0 соответствуют две точки U0, V0 на боковых направляющих звеньях AD и BC, через которые должна пройти образующая k2. Это условие уменьшает степень свободы образующей на две единицы. Задавая в точках U0, V0 касательные к k2, “отнимаем у нее еще две степени свободы. Чтобы зафиксировать единственную оставшуюся степень свободы, следует указать какую-либо дополнительную направляющую l, которая назначается в соответствии с требованиями (техническими, эстетическими), предъявляемыми к конструируемой поверхности.

Пусть, например, оболочка, натягиваемая на контур ABCD, должна пройти через срединную направляющую l=LL′ (рис. 2, б). Чтобы задать касательные к образующей k2 во всех точках направляющих AD и BC, укажем две вспомогательные линейчатые поверхности с плоскостью параллелизма xz и с направляющими AD, p и BC, q. В частности, если p - прямая линия, а q - гладкая кривая, то (AD, p) - коноид, а (BC, q) - цилиндроид. Потребуем, чтобы конструируемая оболочка касалась коноида в точках звена AD и цилиндроида в точках звена BC. Это требование обеспечивает однозначность определения касательных к образующей k2 в точках U, V, пробегающих по боковым звеньям AD и BC опорного контура. Направляющие линии p, q вспомогательных поверхностей назначаются с обязательным соблюдением следующего условия: точки 1 и 2 пересечения направляющей p с плоскостями фронтальных звеньев AB и CD должны быть инцидентны касательным, проведенным к этим звеньям в узлах A и D, а точки 3, 4 пересечения направляющей q с плоскостями фронтальных звеньев должны быть инцидентны касательным к звеньям AB, CD в узлах B и C. В этом случае множество прямолинейных образующих вспомогательного коноида включает в себя касательные к звеньям AB и CD в узлах A, D, а множество образующих цилиндроида включает в себя касательные к этим же звеньям в узлах B, C.

Изменяя форму и положение кривых p и q, можно управлять полнотой конструируемой оболочки подобно тому, как посредством изменения положения управляющих точек осуществляется редактирование поверхности Безье. Графическая часть определителя поверхности состоит из замкнутого контура ABCD, направляющей l=LL и двух вспомогательных линейчатых поверхностей (AD, p) и (BC, q), касающихся конструируемой оболочки вдоль боковых звеньев контура. Покажем, что этими условиями полностью определена единственная поверхность. Произвольному значению параметра u=y0 отвечают точки U0, V0 на боковых звеньях контура, две касательные U0P и V0Q в этих точках (здесь P и Q - точки пересечения линий p, q с плоскостью y=y0) и точка T пересечения направляющей l=LL с плоскостью y0 (см. рис. 2, б).

В плоскости y=y0 получаем пять элементов (три точки U0, V0, T и две касательные U0P и V0Q), полностью определяющие единственную кривую второго порядка - образующую k2 конструируемой оболочки (рис. 2, в). Коника k2, ее центр O, главные диаметры и асимптоты e1, e2 автоматически определяются с помощью программного средства [1].

Изменяя параметр u=y, получаем однопараметрическое множество кривых второго порядка k2, которые формируют непрерывную поверхность, проходящую через заданный контур ABCD. Действительно, если u=yA, где yA - координата y узла A, то точки A, B, L и касательные A1, B3 определяют коническое сечение ALB - фронтальное звено заданного контура. Аналогично, если u=0, получаем другое фронтальное звено данного контура - кривую второго порядка DLC. Следовательно, образующая k2, скользя по боковым звеньям контура, непрерывно меняет свою форму от сегмента конического сечения ALB до сегмента DLC, оставаясь во всех промежуточных положениях кривой второго порядка.

Таким образом, конструируемая поверхность определяется не двупараметрическим множеством табулированных точек (как это реализуется в случае применения идеологии САПР и сшивания поверхности из отдельных участков), а однопараметрическим множеством кривых второго порядка k2. Между точками плана оболочки (плоскости xy) и точками самой оболочки устанавливается взаимно однозначное соответствие, что доказывает ее непрерывность и однозначность. Гладкость оболочки, понимаемая как наличие единственной касательной плоскости в любой точке поверхности (дифференцируемость), есть следствие гладкости управляющих элементов графической части определителя поверхности (направляющих линий и соприкасающихся поверхностей).

На рис. 2 показаны три варианта поверхности: с выпуклой (рис. 2, г), прямолинейной (рис. 2, д) и вогнутой (рис. 2, е) дополнительной направляющей l. В соответствии с вышеописанным алгоритмом, во всех вариантах получается непрерывная гладкая поверхность, образованная однопараметрическим множеством кривых второго порядка, изменяющих свою форму от AB до CD. Заметим, что поверхность с вогнутой направляющей содержит две кривые второго порядка, выродившиеся в прямолинейные образующие a и c (см. рис. 2, е). Очевидно, наличие прямолинейных элементов в каркасе поверхности следует считать ее технологическим преимуществом.

Пример 3. В современной архитектуре используются поверхности, имитирующие естественные природные формы. При этом ставится задача натягивания оболочки на плоский или пространственный криволинейный контур, образованный, в частности, сегментами конических сечений. В этом случае поверхность оболочки может быть построена с помощью кривых второго порядка и линейчатых направляющих поверхностей.

Поверхность (рис. 3, а) образована движением кривой второго порядка, скользящей по направляющей l и плавно изменяющей свою форму от гиперболы g до эллипса e. Три точки образующей на направляющих MN, KL, l (три степени свободы) определяются значением координаты x. Для фиксации двух оставшихся степеней свободы указываем симметрично расположенные коноиды с плоскостью параллелизма yz, соприкасающиеся с конструируемой оболочкой вдоль сторон MN, KL основания. Прямолинейные образующие MT и LT соприкасающихся коноидов проходят через точку T пересечения касательных к входному опорному контуру g и через точки M, L на вертикальных касательных к выходному контуру e. При изменении положения точек M, L меняется полнота конструируемой оболочки.

На рис. 3, б показан купол, натянутый на коньковую линию l и на опорные эллипсы e1, e2. Поверхность образована вращением кривой второго порядка e вокруг оси AB, где A, B - точки пересечения кривых e1, e2. Купол симметричен относительно плоскости zx, поэтому при вращении вершина образующей e скользит по направляющей l; при этом e плавно меняет свою форму от e1 до e2, во всех промежуточных положениях оставаясь кривой второго порядка. Направляющие поверхности вырождаются в плоскости, касающиеся конструируемой оболочки в узлах A, B.

Пусть требуется сформировать гладкую оболочку, натянутую на опорный треугольник AOD и полуокружность e, то есть обеспечить плавный переход от треугольного к круговому поперечному сечению (рис. 3, в). Переходная поверхность образуется движением кривой второго порядка, скользящей по заданной направляющей l и плавно изменяющей свою форму от вырожденной гиперболы AOD до окружности e.

Как и в предыдущем примере, три точки этой кривой определяются значением координаты x. Для фиксации двух оставшихся степеней свободы указываем симметрично расположенные гиперболические параболоиды с плоскостью параллелизма yz, соприкасающиеся с конструируемой оболочкой вдоль сторон DC, AB основания. При изменении положения точек B, C меняется полнота конструируемой оболочки. Если какое-либо звено опорного контура содержит излом, то поверхность сшивается из четырехугольных порций.

Пусть требуется натянуть оболочку на пространственный контур, составленный из дуг окружностей AKD, BKC, ломаной линии ALB и отрезка CD (рис. 3, г). В качестве дополнительных геометрических условий указаны гладкие кривые: коньковая линия KSK, горловая линия OSL, состоящая из дуги e эллипса и отрезка SL (с гладкостью первого порядка в стыковой точке S), и дополнительная направляющая d. Порция поверхности на контуре AKSL формируется подвижной образующей (сегментом кривой второго порядка), меняющей свою форму (при изменении параметра u=x) от дуги AK окружности до отрезка SL. Образующая скользит по направляющим KS, d и AL, соприкасаясь с цилиндрической поверхностью.

Другая соприкасающаяся поверхность - косая плоскость с плоскостью параллелизма yz и направляющими AL и m. Три направляющие (KS, d и AL) совместно с двумя соприкасающимися поверхностями полностью определяют порцию оболочки на контуре AKSL. Аналогично формируем порцию поверхности на контуре ODKS и сшиваем порции (с учетом симметрии относительно плоскости yz). Получаем составную поверхность с гладкостью первого порядка вдоль коньковой линии KSK и с изломом вдоль направляющего отрезка SL. Произвольная образующая, лежащая в какой-либо профильной плоскости - составная кривая, состоящая из двух сегментов кривых второго порядка. В стыковой точке, лежащей на коньковой линии, оба сегмента имеют общую горизонтальную касательную, совпадающую с соответствующей образующей соприкасающейся цилиндрической поверхности.

Пример 4. Пусть требуется сконструировать гладкую (всюду дифференцируемую) поверхность, опирающуюся на прямоугольный фундамент ABCD и касающуюся боковых граней призмы, построенной на этом контуре как на основании (рис. 4, а).

Поверхность формируется при параллельном перемещении образующего полуэллипса e по направляющей g. Кривая e, скользя по g, изменяет свою форму от полуэллипса до прямой AD или BC. Первое семейство образующих состоит из множества полуэллипсов e||zy, опирающихся на стороны AB и CD фундамента. Множество полуэллипсов переменного эксцентриситета, параллельных плоскости xz, составляет второе семейство линий каркаса поверхности.

Поверхность описывается алгебраическим уравнением четвертого порядка. Сечение поверхности плоскостью z=0 распадается на две пары параллельных прямых, что соответствует форме прямоугольного основания. В сечениях вертикальными плоскостями x=a, y=b получаем два семейства эллипсов с переменным эксцентриситетом. Пренебрегая в бесконечно малой окрестности угловой точки слагаемыми третьего и четвертого порядков малости, получаем вместо уравнения купола уравнение эллиптического конуса z2/c02=4xy/a0b0 с осью x=y, z=0 и вершиной в угловой точке. Таким образом, в малой окрестности угловой точки поверхность купола на прямоугольном фундаменте близка к конической поверхности второго порядка.

Для формирования сетчатого каркаса гладкой куполообразной поверхности, опирающейся на треугольное основание (фундамент), также могут быть эффективно использованы сегменты кривых второго порядка с переменным эксцентриситетом. Пусть требуется сконструировать гладкую (всюду дифференцируемую) выпуклую поверхность, опирающуюся на треугольный контур ABC (рис. 4, б). В качестве дополнительного условия, конкретизирующего задачу, может быть указана либо высота купола, либо характерная точка, через которую должна проходить проектируемая поверхность. В вертикальной плоскости, параллельной AC и проходящей через заданную высшую точку D купола, вычерчиваем полуэллипс n, опирающийся концами своего главного диаметра на стороны AB, BC и проходящий через точку D. Выделяем пучок вертикальных плоскостей, параллельных стороне BC, и в плоскостях пучка вычерчиваем образующие полуэллипсы a, опирающиеся своими вершинами на стороны AC, AB и пересекающие направляющий эллипс n. Образующие a заполняют поверхность эллиптического купола на треугольном фундаменте. Произвольная образующая конструируемой поверхности вычерчивается как кривая второго порядка, заданная тремя точками и касательными, указанными в двух заданных точках [1].

В силу симметрии, имеется еще одно (третье) семейство эллиптических образующих b, лежащих в вертикальных плоскостях, параллельных стороне AB. Составим уравнение оболочки, опирающейся на равнобедренный прямоугольный треугольник ABC с катетами, равными единице. Оболочка должна иметь вертикальные касательные плоскости вдоль сторон основания ABC и проходить через некоторую заданную точку D (см. рис. 4, б). Через точку T, бегущую по направляющей n, проходит эллипс y=y0 (1) , где величины полуосей p и q полностью определяются координатами точки T. Из (1) находим координату z точки T, бегущей по направляющей t. Образующий эллипс e, проходящий через T, описывается уравнением, где величины полуосей зависят от положения подвижной точки T.

Чтобы найти зависимость b от x, подставим в (1) выражение y=y0, а вместо z - выражение (1). Учитывая, что 2a=1-x, окончательно получаем уравнение конструируемой поверхности. Таким образом, эллиптический купол на треугольном фундаменте описывается алгебраическим уравнением третьего порядка. Положив z=0, получаем уравнения трех прямых: x=0, y=0, y=1-x, что соответствует форме равнобедренного прямоугольного треугольника ABC, лежащего в основании купола. Положив x=const, получаем уравнение эллипса.

Аналогичным образом, положив y=const или y-x=const, также получаем уравнения эллипсов, что доказывает наличие трех семейств эллиптических образующих на конструируемой поверхности. Если пренебречь слагаемыми третьего порядка малости, то в малой окрестности I угловой точки A получаем уравнение , описывающее поверхность эллиптического конуса с осью x=y, z=0 и вершиной в точке A (см. рис. 4, б). Следовательно, в малых окрестностях угловых точек A, B, C поверхность оболочки близка к конической поверхности второго порядка.

Заключение. Форма кривой второго порядка управляется пятью параметрами. Кубическая парабола управляется восемью параметрами. Следовательно, кубическая кривая более подвижна, чем коника. Из кубических парабол собирают обводы (сплайны), обеспечивающие, например, монотонное изменение кривизны в точке перегиба. Разумеется, с помощью сегментов конических сечений невозможно составить дважды гладкий обвод знакопеременной кривизны, так как коники просто не имеют точек с нулевой кривизной. Все преимущества на стороне сплайн-функций, положенных в основу математических ядер современных отечественных и зарубежных САПР. Тем не менее, нужна альтернатива. Кривые второго порядка применяются в научной и конструкторской работе. В графической САПР обязательно должна быть возможность их построения по любому набору инциденций, визуализации на экране компьютера и использования в инже-нерных расчетах и конструкторской документации, наравне с кривыми Безье, NURBS и др.

Список литературы

1. Короткий, В.А. Синтетические алгоритмы построения кривой второго порядка / В.А. Короткий // Вестник компьютерных и информационных технологий. 2014. - №11. С. 20-24.

2. Волошинов, Д.В. Конструктивное геометрическое моделирование. Теория, практика, автоматизация: монография / Д.В. Волошинов. Saarbrucken: Lambert Academic Publishing, 2010. 355 с.

3. Короткий, В.А. Компьютерное моделирование фигур четырехмерного пространства / В.А. Короткий // Вестник компьютерных и информационных технологий. 2014. № 7. С. 14 -20.

Рисунки к докладу

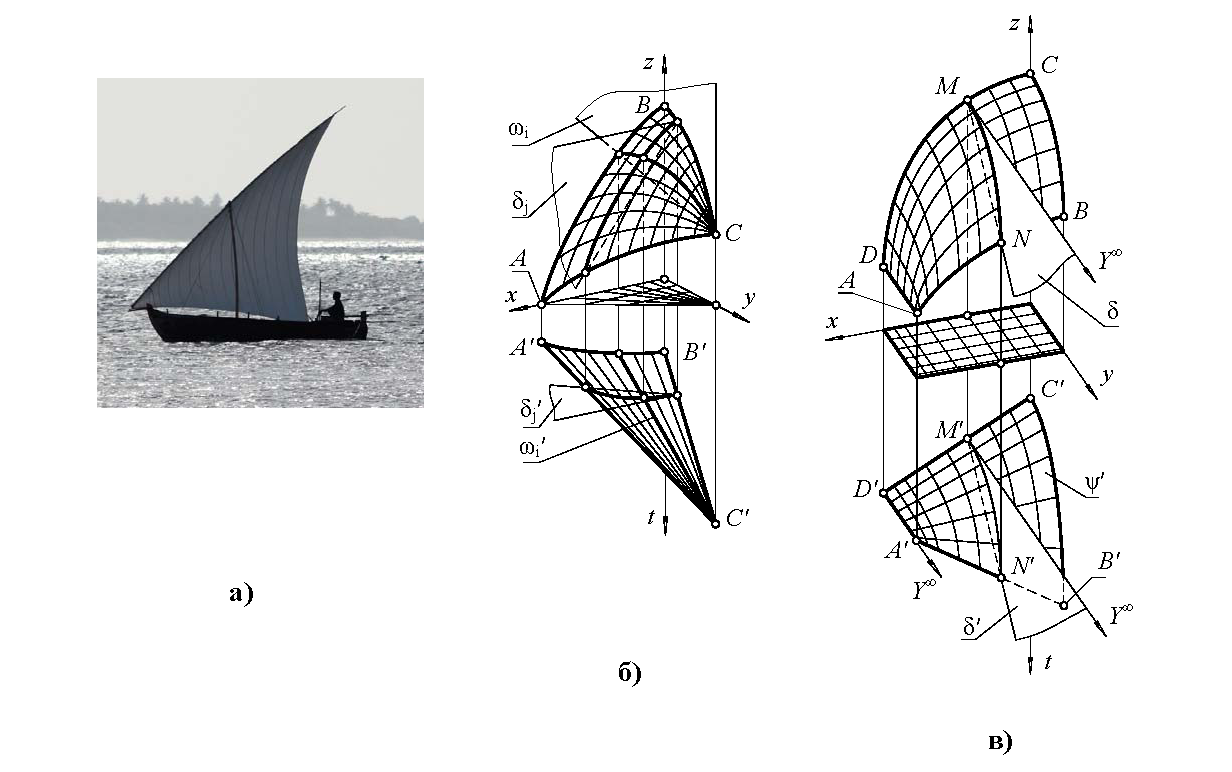
Четырехмерная модель рыбацкой лодки: а - прообраз; б -модель паруса; в - модель фрагмента носовой обшивки

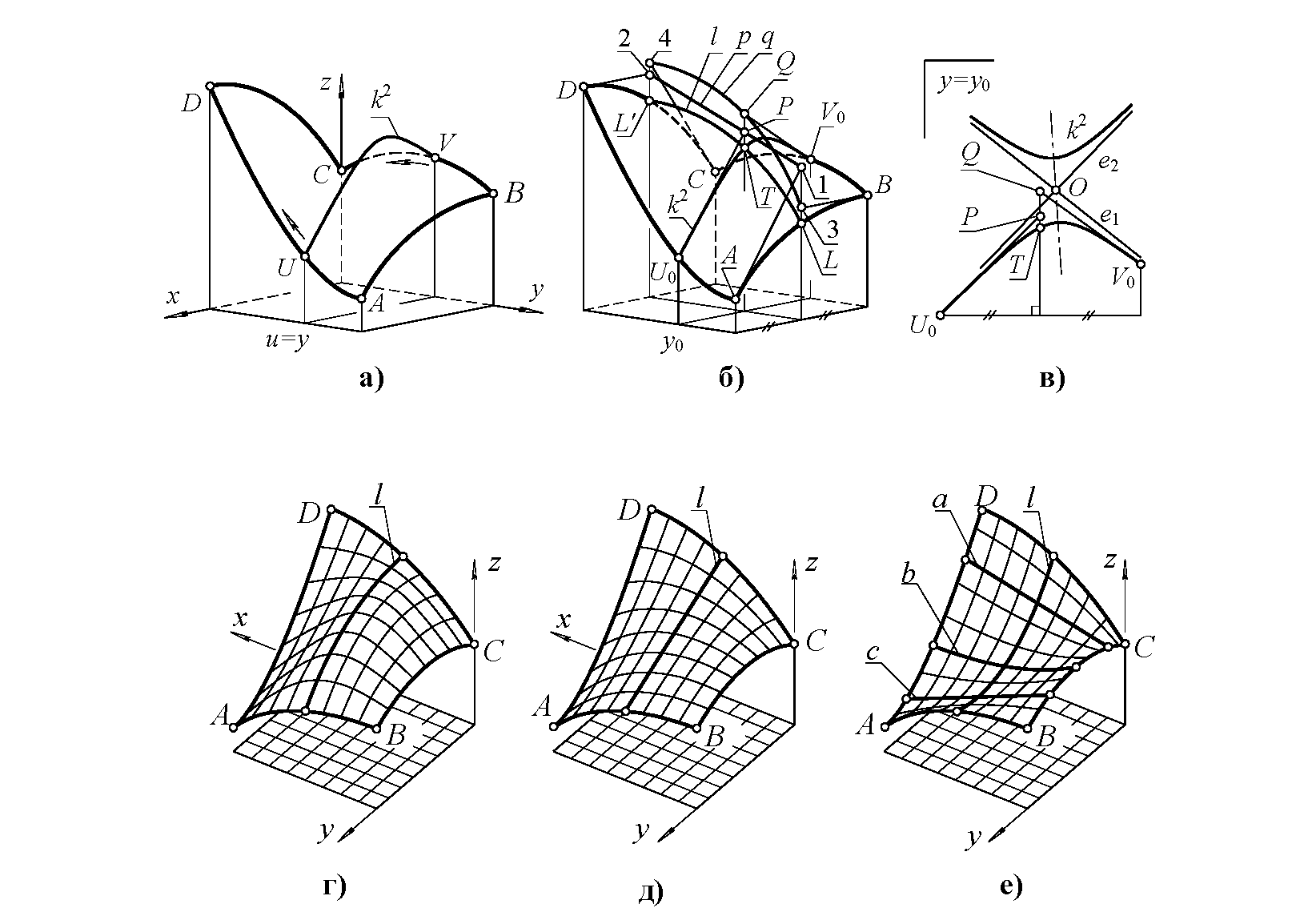
Оболочка на замкнутом контуре: а - опорный контур; б - дополнительные связи; в - сечение y=const; г - выпуклая направляющая; д - прямолинейная направляющая; е - вогнутая направляющая

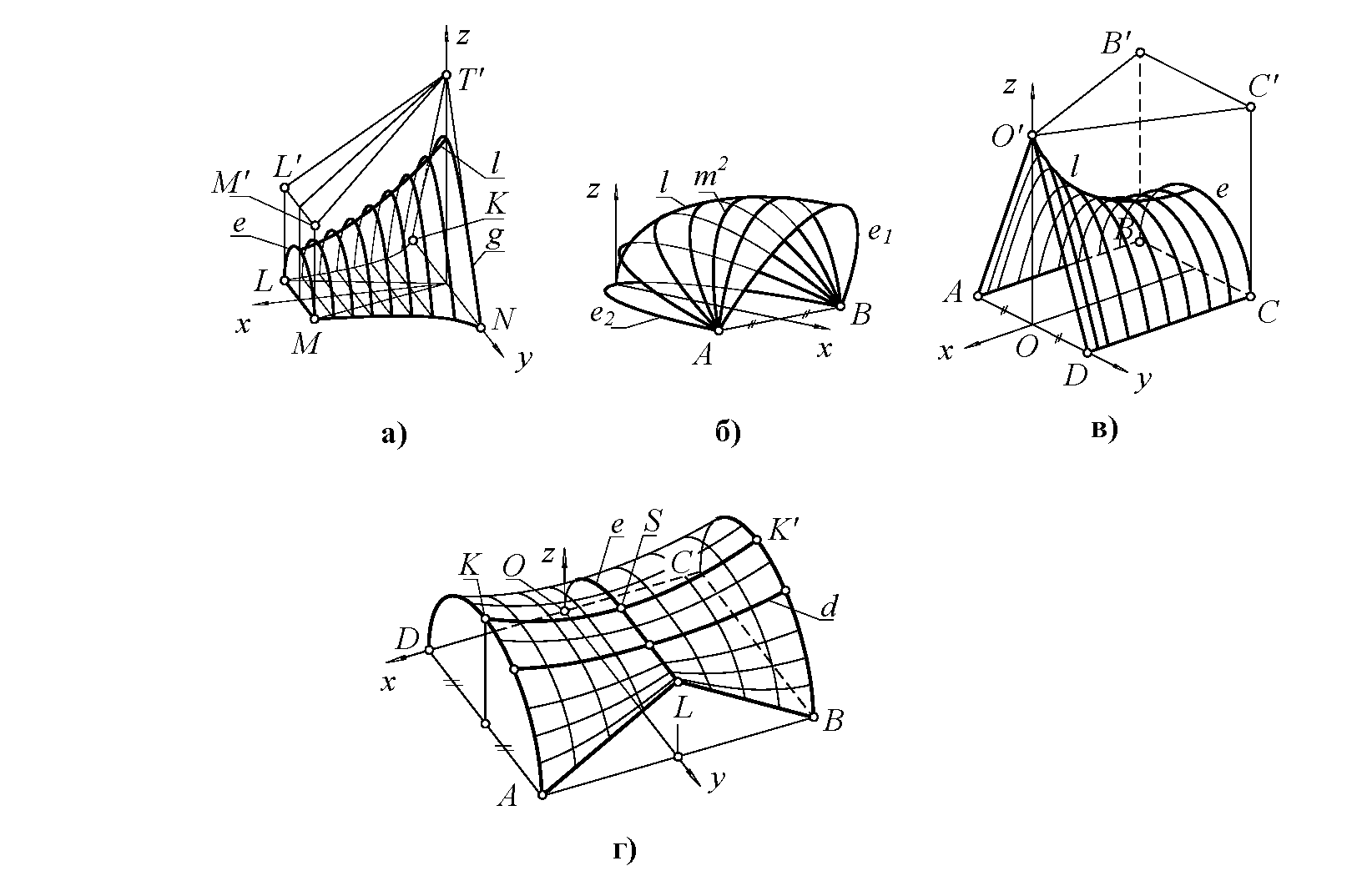
Оболочки: а - на произвольном основании; б- на эллиптическом основании; в - на прямоугольном основании; г - составная оболочка первого порядка гладкости

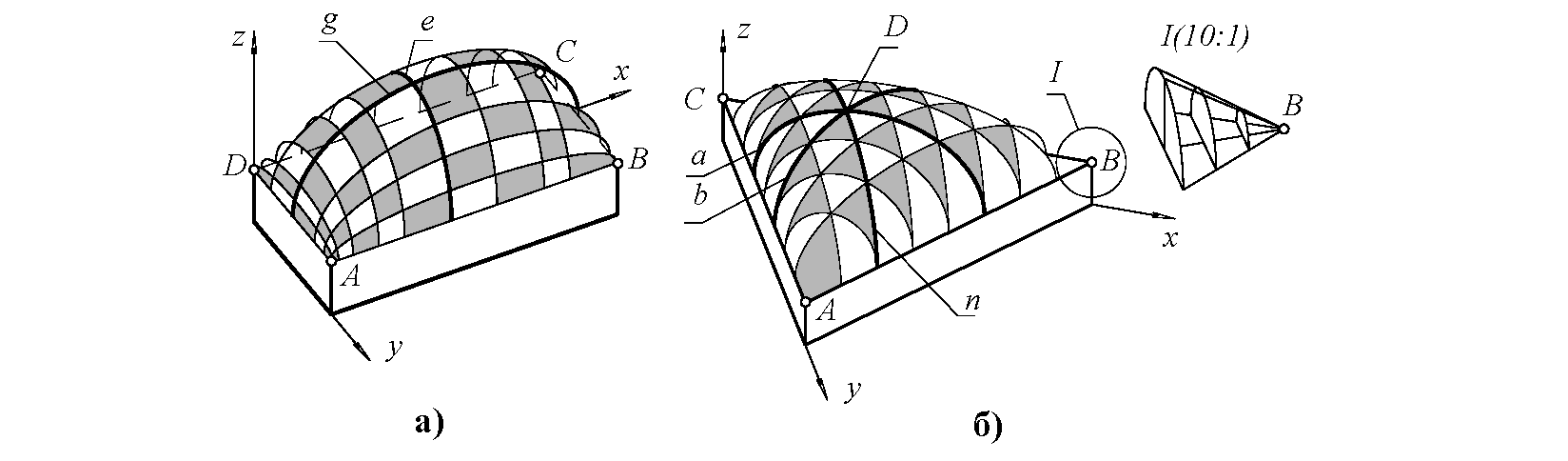
Эллиптический купол: а - на прямоугольном фундаменте; б - на треугольном фундаменте

Принцев Николай Владимирович (13 марта 2015 г. 5:26)	Виктор Анатольевич! Ваш доклад необыкновенно близок мне своим настроем на морскую волну, всё-таки Питер - Морская Столица России! Когда к Вам пришло увлечение парусной тематикой?
Гирш Антон Георгиевич (13 марта 2015 г. 16:36)	Здравствуйте, Виктор Анатольевич! Приятно, что решили выставить доклад на актуальную тему конструирования поверхностей по наперёд заданным граничным условиям. Это, пожалуй, наиболее плодотворная ниша для приложения творческих усилий геометров-прикладников кафедр инженерной графики. Выход в пространство более высокого измерения для решения задачи данного пространства применялся и раньше и всегда давал хорошие результаты. Хочу дать популярный пример для участников конференции: На плоскости даны две окружности. Построить параболу, описанную около данных окружностей. Машинное решение не проходит, значит надо начинать думать. Решение с выходом в R3: В окружности вкладывают два шара и описывают около них конус. Сечение конуса плоскостью, несущей окружности, есть искомая парабола. Так и из R3 можно выйти в пространство R4 для решения задачи конструирования поверхности, которое приведено в докладе. Идея доклада – это свежая струя, которая несёт новые конструктивные возможности. Ваш доклад показал, что коники ещё рано сдавать в архив, они показали ещё и динамические свойства. Ещё Ваш доклад интересен тем, что не ограничивается имеющимся инструментами машинной графики, а ставит перед разработчиками требования новых инструментов, необходимых пользователям. С уважением, Антон Георгиевич Гирш.
Панчук Константин Леонидович (13 марта 2015 г. 18:36)	Здравствуйте, Виктор Анатольевич! Несколько вопросов относительно гладкости конструируемых  Вами  поверхностей на основе коник.  1. По известному определению гладкости кривой линии кубическая парабола  y=t1/3 (в степени одна третья), x=t в интервале изменения t от -1 до 1  в нуле не имеет непрерывной производной, т.е. не является гладкой по определению. Но при другой параметризации y=sht, x=sh3t в интервале от -бесконечности до +бесконечности  эта кривая становится гладкой. Аналогичный пример можно привести для полуокружности. Т.е. гладкость кривой не является инвариантом  параметризации. Вопрос: как ведут  в отношении гладкости Ваши поверхности при смене параметризаций?  2. Известны гладкость Ck (классическое математическое представление) и Gk (геометрическая гладкость). Из первой всегда следует вторая. Но не всегда из второй следует первая. Как в Ваших конструктивных построениях поверхностей ведут себя эти гладкости. Рассматриваете ли Вы их в принципе? 3. Какие max-ые степени гладости конструируемых поверхностей Вы получаете? Благодарю Вас. С уважением К.Л. Панчук
Короткий Виктор Анатольевич (14 марта 2015 г. 21:32)	1. Николай Владимирович! Вы правы. Тема близка. Моряк моряка видит издалека. 2. Антон Георгиевич! В геометрическом архиве утонули не только коники. Но мы еще походим под парусом геометрии. И с "Компасом". Прекрасное сочетание. 3. Константин Леонидович! С параметризацией все просто. Действует "презумпция гладкости": кривую называют гладкой, если существует такая параметризация x(t), y(t), что эти две функции имеют непрерывные производные, не обращающиеся одновременно в ноль. Геометрически: гладкая кривая не имеет угловых точек, гладкая поверхность не содержит изломов. Разве это не строгое определение? О степени гладкости идет речь, если имеем составную поверхность или обвод. В статье использован алгоритм [2] формирования поверхности, несущей на себе двупараметрическое множество гладких кривых (коник). Через каждую точку поверхности проходят две коники (или коника и кривая 4 порядка, полученная в сечении коноида 4 порядка). Всякая кривая одного семейства пересекает все кривые другого семейства. По сути, это кинематический способ. Получается поверхность, не имеющая изломов! Она заметается гладкой кривой - коникой с переменным эксцентриситетом. Нельзя ответить на вопрос, какова ее степень гладкости. Это не составная поверхность. Для некоторых частных случаев удается написать ее ур-ние. Получается 4 порядок для четырехугольной рамки и 3 порядок алг уравнения для треугольной рамки (в статье этих уравнений нет, их "не пустил" формат конфереции. Какова степень гладкости поверхности, описываемой уравнением 4 порядка? Вопрос некорректный. Видимо, я чего-то не понимаю.  С уважением, моряк-теоретик Короткий Виктор Анатольевич
Головнин Алексей Алексеевич (15 марта 2015 г. 1:17)	Уважаемый Виктор Анатольевич, прочитываю все доклады, пытаюсь с Вашей подачи знакомиться с многомерной геометрией. Дополнительную информацию собирать пока не намереваюсь, поэтому она остается для меня большой загадкой. И если переход в 4Д остается на вере, а его визуальное представление – неприятие (связанное с моей недостаточной математической подготовкой), то приведенный Антоном Георгиевичем пример полезного перехода от 2Д к 3Д представляется наглядным. Это уже второй пример Антона Георгиевича на этой конференции, которые представляю полезными для себя. Но вместе с тем вопрос, который, наверное, к Антону Георгиевичу. Уважаемый Антон Георгиевич! Обязательно ли говорить в Вашем примере о параболе, касательной к двум окружностям, как о примере изменения размерности? Можно ли его отнести к теме о сечениях конуса? С уважением Головнин А.А.
Гирш Антон Георгиевич (15 марта 2015 г. 16:31)	Уважаемый Алексей Алексеевич, спасибо на добром слове. Приведённый пример относится к вопросу выхода в пространство более высокого измерения для решения актуальной задачи в исходном пространстве, 2Д--> 3Д. Знание о конических сечениях, безусловно, предполагаются. Поскольку 4Д представить себе человеку не дано, то действия проводятся по формальной схеме. Короткий В.А. даёт такой формальный алгоритм и достигает результат. Считаю его доклад полезным тем, что он не пропагандирует и не драматизирует 4Д-пространство, а просто рассматривает его как инструмент. К таким переходом надо привыкать и пользоваться ими - это будущее прикладной геометрии. С уважением и спасибо за интересный вопрос. Гирш А.Г.
Панчук Константин Леонидович (15 марта 2015 г. 16:52)	Виктор Анатольевич! Я о чем! Поверхность гладкая класса Ck (k -степень), если (в случае ее параметрического представления) правые части параметрических уранений поверхности, будучи функциями двух параметров, допускают непрерывные производные до поряка k включительно и при этом ранг матрицы частных производных (из двух строк xu yu zu  и  xv yv zv) равен 2 в каждой точке (u,v) области параметров.  Известные примеры из теории поверхностей евклидова пространства:  прямой геликоид  - гладкая поверхность класса C∞;  cфера, эллиптический параболоид - гладкие поверхности того же класса гладкости (степень k=∞). Класс гладкости поверхности сохраняется при той перепараметризации, при которой якобиан отображения в параметрической области не равен нулю. Какие Ваши поверхности с этой  точки зрения? Что можно сказать об их Ck? Я думаю, что эти вопросы не праздные. В прикладных задачах, связанных с конструированием технических поверхностей  и удовлетворяющих определеным динамическим, прочностным, функциональным и иным показателям, эти вопросы непременно возникнут.  С уважением, Панчук К.Л.
Гирш Антон Георгиевич (15 марта 2015 г. 16:55)	Уважаемый Константин Леонидович, Вы интересуетесь вопросом гладкости поверхностей, построенных Коротким В.А. На мой взгяд вопрос неправомочен. Можно говорить о гладкости обвода, например, обвода линий. Тогда это вопрос о степени гладкости (определение Осипова В.А.) в точке стыковки: 1. Непрерывность линии. (Когда-то Якунин В.И. предлагал обвод без точек стыка - невязка лежала в зоне допуска.) 2. В точке стыка нет общей производной (есть излом). 3. В точке стыкоки существует общая производная (касательная). 4. В точке стыкоки существует общая вторая производная (круг кривизны) и т.д.  Аналогичный подход существует и в отношении обводов поверхностей. Имея единую поверхность нельзя её оценивать как обвод. Она может содержать рёбра и др. сингулярности, но это её свойства. Спрашивать можно о свойствах полученной поверхности, но это другой вопрос. С уважением, Гирш А.Г.
Панчук Константин Леонидович (15 марта 2015 г. 18:19)	Уважаемый Антон Георгиевич! Спасибо за ответ. Относительно "....Вы интересуетесь вопросом гладкости поверхностей, построенных Коротким В.А. На мой взгяд вопрос неправомочен....".  Вопрос о гладкости получаемых поверхностей присутствует во всех примерах конструирования. Позвольте привести содержание нескольких задач, рассматриваемых  автором. В примере2: требуется построить непрерывную гладкую (не имеющую изломов) поверхность, проходящую через данный замкнутый контур.  В примере 4: требуется сконструировать гладкую (всюду дифференцируемую) поверхность, опирающуюся на прямоугольный фундамент ABCD и касающуюся боковых граней призмы, построенной на этом контуре как на основании. Как, видите, автора также интересует "неправомочный" вопрос гладкости конструируемых поверхностей. В каждом из расмотренных в докладе примеров имеются цельные (не "сшитые") алгебраические поверхности и среди них есть простые (без особых элементов).  Вопрос о принадлежности их классу гладкости Ck вполне правомочен. Для каждой из сшиваемых в единую поверхность порций он также правомочен. Вопрос сшивки порций - он, видимо увязан с классом гладкости сшиваемых порций.  С уважением, Панчук К.Л.
Короткий Виктор Анатольевич (16 марта 2015 г. 15:47)	Уважаемые спорщики Антон Георгиевич, Константин Леонидович! Продолжаем р-ривать скользкий вопрос о гладкости. 1. "Гладкость" есть локальное свойство линии или поверхности. То есть сам термин явно из дифф. геометрии. Но в известном учебнике Выгодского Диф. геом такого термина нет вообще. Также нет понятия степень гладкости. В диф. геом. Бюшгенса - тоже нет такого понятия. Почему? Не знаю. Согласен, на учебник Выгодского ссылаться нельзя (устарел: 1949 год издания). Но переиздание учебника Бюшгенса было недавно.  2.Предъявим к линии в данной ее точке следующие требования: непрерывность и существование касательной, причем положение касательной меняется непрерывно (последнее требование должно излагаться на языке эпсилон-дельта). И еще одно требование - вектор-функция, описывающая нашу кривую, должна иметь в исследуемой точке отличную от нуля производную (чтобы исключить возможность точки возврата второго рода - клюв с общей касательной). С целью сокращения текста, вероятно, сумму этих требований называют "гладкостью"? Но кто ввел этот термин? И когда? 3. Причем несуществование производной вовсе не обязательно означает несуществование касательной в этой точке. Например, окружность можно так прекрасно параметризовать, что у нее в отд точках скорость (производная вектор-функции) будет меняться скачком (Выгодский, стр. 43, примечание). 4. К конструируемой в статье поверхности предъявляется требование гладкости. Это сокращенное обозначение ряда требований: непрерывность и существование непрерывно меняющейся касательной плоскости (дифференцируемость). Автора (то есть меня), разумеется, интересует вполне правомочный вопрос гладкости (отсутствие изломов и дифференцируемость). Но не вопрос о степени гладкости конструируемой поверхности! Степень гладкости - это кратность дифференцируемости. В некоторых частных случаях, когда удается описать поверхность алг ур-ием, можно сказать, что ее Ck равен бесконечности. Если нет уравнения, то получаем графически заданную поверхность. Как определить Ck произвольной графически заданной (начерченной от руки на листе бумаги) кривой? Вполне можно сказать: "степень гладкости гиперболы равна бесконечности". Много ли информации в этом утверждении?   5. Поэтому. Степень гладкости - дифференциальная характеристика не поверхности, а локальная х-ка либо стыковой точки обвода, либо линии сшивания поверхностей. Например, с удовольствием могу предложить геометрический алгоритм ("циркулем и линейкой"!) стыковки двух коник с гладкостью третьего порядка в стыковой точке (четырехточечное соприкосновение). Продолжаем разговор? С уважением, алгебраист Короткий В.А
Панчук Константин Леонидович (17 марта 2015 г. 17:45)	Уважаемый Виктор Анатольевич! И все-таки,степень гладкости - это дифференциальная характеристика поверхности (элементарной, простой, кусочно-гладкой). С великим удовольствием даю ссылку на моих заочных учителей, книги которых изучал, обучаясь много лет назад в аспирантуре.   Атанасян Л. С., Базылев В. Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 е.: ил. § 55. Гладкие поверхности стр. 203 http://issuu.com/normagee/docs/atanasjan_-bazylev_-geometrija.chast_2_1987/205?e=0   Базылев В. Т. и Дуничев К. И. Геометрия. Часть 2. Учеб. пособие для студентов физ.-мат. фак-тов пед. ин-тов. М. «Просвещение», 1975.-367 с. с ил. С уважением, Панчук К.Л.
Короткий Виктор Анатольевич (17 марта 2015 г. 18:55)	Константин Леонидович! Принято. Спасибо. С уважением, вечный студент Короткий В.А
Гирш Антон Георгиевич (22 марта 2015 г. 17:19)	Виктор Анатольевич, здравствуйте! Немного не по теме. "Построение коники по любому набору точек и касательных общим числом 5 (всего 53 варианта) со всеми алгоритмами дано в пособии Короткий В.А Проективное построение коник. Пособие есть в инете в формате ПДФ." Якоб Штайнер первым определил 51 вариант коник по исходнам пяти элементам, но это число оказалось ошибочным и после уточнялось. Как Вы пришли на число 53, по формулам параметризации или эмпирически? Далее по теме конференции я хотел привлечь внимание участников, что есть человек, который подсчитал число всех задач начертательной геометрии. И это число небольшое. В.В.Глоговский. Элементарные конструктивные задачи по начертательной геометрии. - Львов: ВШ, 1981. - 152 с. У него было ещё стихотворение про нерадивых студентов. Помню только начало "Трудно видеть связь проекций, пропустив 12 лекций. ..." Это ж из скольки лекций состоял семестр по НГ, если только проекционную связь доносили на 12 лекциях? Всем желаю полезного общения. С уважением, А.Г. Гирш.
Короткий Виктор Анатольевич (22 марта 2015 г. 18:51)	Антон Георгиевич, добрый день!  1. Дело в том, что мое пособие "Проективное построение коники" - имеет учебный характер. На кого рассчитано? Не знаю, что ответить. Например, какому нибудь сумасшедшему конструктору вдруг резко потребовалось начертить, например, гиперболу "по двум параллельным касательным, точке и направлениям асимптот". А такой кнопки или параметризации, черт возьми, в его графическом редакторе и нету. А ему надо! Ну вот в пособии и дается четкий пошаговый алгоритм, как это сделать. Циркулем и линейкой! То есть вычерчивая на экране компа в устаревшем "режиме 2D" черточки и кружочки. Не хочет возиться? Пожалуйста. К его услугам составлена программа на автолиспе. Начерти на компьютере в устаревшем и никому не нужном 2D исходные инциденции - и готово. Результат - главные оси плюс асимптоты плюс непрерывно вычерченная коника, проходящая через заданные точки касательно к заданным прямым. Никаких итерационных схем! ПРОСТО ГЕОМЕТРИЯ. Проективная или начертательная? А надо ли их разделять? Да и кому они обе сейчас нужны? Нужно ли вообще преподавателю графических дисциплин знать геометрию хотя бы в пределах педвуза? Может, ему вполне достаточно уметь "вращать", "выдавливать" и "лофтировать" и знать назначение пары десятков кнопок трех-пяти графических пакетов? Короче, есть пособие по проективно-конструктивным методам вычерчивания коник. Для сумасшедшего конструктора.  2. При подсчете числа сочетаний я позволил себе считать отдельным образом те варианты, в которых участвуют несобственные элементы. С точки зрения тех проективных алгоритмов, которые забиты в программе - такое выделение бессмысленно. В программе можно на равных правах  указывать как собственные, так несобств точки искомой коники. Но в учебных целях я выделил все аффинные варианты. Получилось 53 варианта. Разумеется, это плохой, эмпирический и внутренне противоречивый счет. Разве можно, например, особо выделять проективный алгоритм, в котором участвуют параллельные касательные? Конечно, нет. Поэтому цифра 53 - условная, для удобства справочного использования пособия. За такой счет Якоб Штайнер нас бы по головке не погладил. Он бы вообще не стал с нами разговаривать. С уважением, сумасшедший Короткий Виктор Анатольевич