

|
Лепаров Михаил Николаевич | (Технический университет -София) |
В настоящем докладе рассматриваются геометрические преобразования заданной сборочной единицы с целью получения ее варианта. Под вариантом понимается новое изделие, которое соответствует требованиям: выполнение той же главной функции как рассматриваемого изделия и отличается от заданного изделия по характеристикам деталей (форма, число, расположение) и / или соединениями между ними. Предлагается классификация геометрических преобразований и эвристические методы их реализации. Методы представлены их эвристическими алгоритмами и иллюстрируются примерами.
Одним из важных вопросов проектирования технических объектов является генерация вариантов решений и выбор из них оптимальнного. Под вариантом заданой сборочной единицы (СЕ) в настоящей работе понимается новая СЕ, которая отвечает требованиям:
а) полученая на основе первичной заданной СЕ;
б) выполняет ту же главную функцию как и заданый объект
в) реализована иначе по отношению к заданной за счет других деталей и / или соединений между ними и / или основных функций.
Основным методом поиска вариантов является метод геометрических преобразований СЕ. Общие способы поиска вариантов за счет геометрических преобразований в настоящей работе названы операциями над СЕ.
Цель данной работы заключается в систематизации основных операций над СЕ, эффективных для поиска ее вариантов и выявление новых вариантов использования ряда операций.
Систематизация и методы разработаны автором на основе логического анализа.
Обзор ряда источников показывает, что проблема сущности операций над СЕ, исключая некоторые общие рекомендации, другими исследователями практически не рассматривается, при этом ряд методов поиска вариантов технического объекта представлены автором статьи в [1-14 и др.].
Классификация базовых операций по различным признакам приведена в таблице 1. Она получена путем анализа различных способов поиска вариантов. Каждая классификация, в т.ч. и таблице 1, является неполной и может быть расширена по горизонтали по отношению видов решений, по вертикали по отношению видов классификационных признаков, по диагоналям - создание дополнительных классификациий отдельных решений (субклассификаций).
Применение классификации:
- для уточнения возможности (пути) поиска вариантов CE;
- в качестве отправной точки для создания мегаметодов и методов для поиска вариантов данной СЕ;
- в качестве основы для дальнейшего развития и углубления исходной классификации.
Таблица 1
Классификация возможных геометрических преобразований СE
|
Классификационный признак
|
Геометрические преобразования
|
|
1. Тип преобразования (операции)
|
1.1. Симметрия
1.2. Трансляция
1.3. Вращение
1.4. CAD функции
1.5. Замещение
1.6. Модификация
1.7. Трансформация
1.8. Рекурсия
1.9. Неясность
1:10. Ошибка
1:11. Инверсия
1:12. Преобразование
1.13. Систематизация
1.14. Комбинация
1.15. Др.
|
|
2. Область применения преобразования
|
2.1. СЕ как единное целое
2.2. Часть СЕ (определенное количество деталей)
2.3. Деталь как одиное целое
2.4. Часть детали
|
|
3. Этапы геометрического проектирования
|
3.1. Формы деталей
3.2. Расположение деталей
3.3. Соединения между деталями
3.4. Комбинации форм, расположения и соединений
|
|
4. Рассматриваемое описаниие СЕ
|
На базе:
4.1. Главной функции
4.2. Черного ящика
4.3. Инженерной идеи
4.4. Основных функций
4.5. Физического принципа действия
4.6. Общих функций
4.7.Функций Колера
4.8. Составных частей
4.9. Их разницы
4.10. Описания действия
4.11. Математических зависимостей
4.13. Упрощенного сборочного чертежа
4.14. Рабочей документации
4.15 Структуры
4.16. Другого вида
|
|
5. Представление заданной СЕ
|
В виде
5.1. 2D
5.2. 3D
5.3. Схематическом
5.4. Текстовом
|
|
6 Способ получения
|
6.1. Почти формализованной вариантности
6.2. Неформализованной вариантности
|
Симметрия (пункт 1.1 таблица 1), трансляция (1.2) и вращение (1.3) широко известные геометрические преобразования, и поэтому не нуждаются в специальном представлении.
CAD функции (1.4): преобразования на основе функций CAD системы, которые служат для построения объекта.
Замещение (1.5) [16]: взаимствование материализации объекта- донора по заданному описанию объекта- реципиента (данным СЕ).
Модификация (1.6) [17]: изменение объекта путем поиска вопросов по вариантам существенных слов текстового описания объекта.
Трансформация (1.7) [17]: изменение объекта путем измения части его текстового описания.
Рекурсии (1,8) [18]: операция, состоящая в приложении над заданной СЕ совокупности предварительно выбранных методов с целью получения новых вариантов СЕ.
Неясность (1.9) [19-22]: поиск экспертом (экспертами) варианта заданной СЕ, которая сознательно представлена неоднозначно (неполно) другим экспертом (экспертами).
Ошибка (1.10) [23]: поиск экспертом (экспертами) варианта заданной СЕ, в которой сознательно допущена ошибка другим экспертом (экспертами).
Инверсия (1.11) [24]: операция над объектом, в которой один элемент объекта заменяется другим, который выбирается из списка предварительно классифицированных по существенным признакам элементов.
Преобразование (1.12): последовательно используется совокупность методов в следующем порядке: первый метод - используется на исходной, заданной, СЕ, второй метод используется на полученном результате использования первого метода и т.д. с последовательным применением располагаемых методов.
Систематизация (1.13): последовательно используется совокупность методов следующем порядке: первый шаг- каждой метод из совокупности методов используется на заданной СЕ, второй шаг- каждой метод совокупности используется на каждый из результатов, полученных на первом шаге и т.д.
Комбинация (1.14): комбинирование элементов двух вариантов.
Другое (1.15): эвристический характер решаемой проблемы -"поиск новых вариантов CE" естественно предполагает , что кроме предложенных операций, существуют и другие, неизвестные автору и / или те, которые предложены в будущем.
Виды описаний СЕ (пункт 4, таблица 1) определены в [15,25,26]. Остальные геометрические преобразования из таблицы 1 ясны из их наименований.
Операции "рекурсия", "преобразование" и "систематизация" представляют собой отдельную группу. Для их реализации требуется не один, а множество методов, которые обычно используются в остальных операциях.
Под “мегаметодом” в данной работе понимается метод, на основе которого могут быть созданы семейство конкретных методов.
Общий алгоритм
1. Выбрается возможное геометрическое преобразование объекта (плоская фигура или пространственное тело) – табл. 1, п. 1.
Выбор упрощается наличием метода применения этого преобразования, как и знакомство с ним. Этот метод в дальнейшем будет называться "Обобщенный метод."
2. Разрабатывается классификация выбранного геометрического преобразования. Информация о такой классификации можно найти во всех доступных нам источниках информации, а также используя аналогию с другими существующими классификациями.
Классификация определяет варианты рассматриваемого преобразования. В некоторых случаях классификация может быть пустой.
3. Выбирается вариант геометрического преобразования (п. 3) или комбинация вариантов.
4. Полученный вариант используется в качестве операции над заданной СЕ.
Если в п. 1 найденый метод является обобщенным, то варианта геометрического преобразования реализуется с помощью собственого алгоритма. Если найденный метод не является обобщенным, то необходимо составить алгоритм по аналогии с алгоритмами существующих методов геометрических преобразований.
Ниже приведены некоторые из возможных способов применения операций. Следует подчеркнуть, что каждая операция может быть реализована с помощью нескольких методов.
Алгоритм
1. Анализируется заданная СЕ с точки зрения ее симметрии относительно плоскости, проходящей через нее. Если плоскость симметрии отсутствует, то любая другая плоскость или ось может быть принята в качестве плоскости (оси) симметрии.
Вариант: устраняются все детали, которые являются причиной ассиметричности СЕ.
2. Проверяется наличие составных частей СЕ, которые не могут быть изменены. Неизменяемыми частями СЕ являются те части, чьи внутренные поверхности и соединения не могут быть превращены во внешние (напр. лампы, подшипники, шестерни и т.п.). Эти части также отстраняются.
3. Далее будем называть полученную СЕ "старой СЕ" и ее ось (плоскость) симметрии - "старой осью( плоскостью)”. Удаляется одна половина "старой СЕ". При этом изображение оставшейся половины СЕ для дальнейшего будем называть "исходное изображение".
4 "Старая ось" "исходного изображения" движется параллельно самой себе до тех пор, пока не достигнет контура или пройдет через него. Это её положение определяет ось симметрии преобразованной СЕ и будет "новой осью".
5. Линия, изображающая выходное положение "старой оси” заменяется сплошной линией (контуром) в местах, где она пересекает соответствущие детали СЕ.
6. Выполняется зеркальное изображение по отношению к "новой оси" "исходного изображения."
7. Оформляется вариант изделия, имея ввиду особености деталей и с учетом того, что в действительности "исходное изображение” описывает пространственную ротацию вокруг „новой оси”. Далее добававляются линии находящиеся позади проекционной плоскости.
Важно отметить, что пространственное вращение не является обязательным. Возможна и зеркальная трансляция частей СЕ, а также и комбинация - для одних частей совершается ротация, а для других- трансляция. Все это увеличивает возможности поиска новых вариантов. Следует отметить, что в некоторых случаях невозможно проведения выбора, например при наличие резьбы, ротация неизбежна, так как она не может существовать другим образом.
8. Вводятся в подходящих местах устраненные в п.1 и п.2 детали.
9. При необходимости с т.з. функционирования, сборки и разборки, вводятся соответствующие изменения в формах деталей и/ или их соединений или добавляются другие подходящие детали, вкл. и восстановление первоначальных форм некоторых из них.
Примечание. Если в п.1 установлено отсутствие плоскости симметрии выходной СЕ и была принята плоскостью симметрии СЕ характерная плоскость или ось СЕ, то последняя разделяет СЕ на две части. В этом случае п.п.2-9 алгоритма применяются независимо для каждой из частей.
Пример
На рис.1д представлена иллюстрация второго асимметричного технического объекта. По отношению к ему алгоритм может быть применен 4 раза: при принятии оси I-I за плоскость симметрии алгоритм может применятся дважды для левой и правой по отношению к этой оси частей СЕ; остальные два раза образуются при принятии оси ІІ-ІІ за плоскость симметрии.
Алгоритм
1. Уточнение проблемы.
2. Построение главной проекций исходного объекта. Возможно использование нескольких проекций.
3. Для каждой проекции: определяются возможные секущие плоскости.
4. Для каждой их них:
4.1. Определяются части выходной СЕ, полученые в результате деления последней рассматриваемой плоскостью.
4.2. Для каждой из полученных частей:
4.2.1. Строится симметричное изображение по отношению к контуром изображения.
4.2.2. Оформляется полученный вариант с т.з. функционирования и сборки и разборки. В случае необходимости вводятся соответствующие изменения в формы и расположение деталей, а также вводятся новые или исключаются некоторые из съществующих деталей.
Примечание. Алгоритм может применятся как для всей CE (п. 2.1 табл. 1), так и для ее частей (п. 2.2 табл. 1).
Пример
В этом методе условно принимается, что некоторые из деталей или все детали выполнены из эластичного материала, а цель этого метода является мысленный выворот СЕ наизнанку. Далее для этого будем использовать термин „выворот”.
Алгоритм
1. Анализ выходной СЕ.
В зависимости от вида СЕ возможны различные подходы, а для некоторых СЕ каждый из подходов пригоден и приводит к различным результатам:
2. Выбор подхода осуществления метода. Накопленный опыт реализации метода облегчает выбор. В противном случае, применяются все подходы.
3. Выворот наизнанку:
3.1. (I подход)
3.1.1. Уточняется направление вывората. В принципе существуют различные варианты выбора возможных направлений, но они зависят от местоположения полостей в конкретной CE.
3.1.2. Выбор части поворота. Так как выворот формально совершается за счет поворота части СЕ вокруг точки, следует выбрать часть и точку поворота. Если СЕ является симметричной по отношению направления выворота, частями поворота является обе части СЕ.
3.2. (II подход)
3.2.1. Выбор секущей плоскости. Если СЕ является симметричной по отношению направления выворота, то секущей плоскостью является плоскость симметрии или плоскость расположенная параллельно ей.
3.2.2. Выбор части поворота.
3.2.3. Уточнение направления выворота.
3.3. (III подход)
3.3.1. Уточнение деталей, которые не должны выворачивается.
3.3.2. В зависимости от типа CE (полостей) применяются действия одного из основных подходов – п.3.1 или п.3.2.
4. Выворачивание путем повората соответствующей части.
Примечание. Есть две возможности: а) выворачивание по отдельности двух частей CE и их объединение далее и б) выворачивание одной из частей и добавление к ней симметричного изображения. При III подходе к вывернутым частям добавляются части, которые не выворачиваются.
5. Оформляется полученный вариант с контролем функционирования, сборки и разборки. В случае необходимости вводятся соответствующие изменения в формы и расположение деталей, а также вводятся новые или исключаются некоторые из существующих деталей.
Пример
Алгоритм
1. Уточнение проблемы.
2. Построение схематической или более подробной модели (моделей) объекта (2D, 3D). Для этой цели может быть использовано и одно из существующих решений рассматриваемого технического объекта.
3. CAD система:
3.1. Выбор CAD системы. Одним из существенных условий выбора является знакомство человека с данной системой.
3.2. Составление списка основных команд системы, напр. Rotate, Move, Mirror и др.
3.3. Для каждой команды включонной в список:
3.3.1. Анализ команды с т.з. ее возможности изменить модель (п. 1).
3.3.2. Использование команды ко:
а) всей модели и / или
б) части модели.
3.3.3. Проверяется получено ли решение рассматриваемой проблемы (п.1).
Примечание. При необходимости с позиции контроля функционирования, сборки и разборки СЕ, вводятся соответствующие изменения.
4. Комбинирование команд- часть объекта выполнается с помощью одной команды, а другая часть- с помощью другой.
5. Комбинирование решений.
Примечание. Нет препятствий для применения метода в ручном режиме.
Пример
Метод "Контрольные вопросы" в эвристике представляет набор независимых рекомендаций, каждая из которых состоит из положительного прошлого опыта, представленого в виде одного или нескольких предложений. Здесь легче всего использовать составной метод, используя основные идеи методов, реализующих соответствующие операции. Такую возможность представляет таблице 1, в которой обобщены основные идеи геометрических преобразований СЕ. Ниже предложен один из таких методов.
1. (Симметрия) На ½ (части, всей) СЕ выполняется симметричное изображение. Увеличения числа вариантов производятся за счет изменения направлений операций для каждого из ранее полученных резултатов.
2. (Симметрия) Определяется тип CE- симметричный или асимметричный. Изменяется тип симметрии. То же самое осуществляется для каждой из деталей СЕ.
3. (Трансляция) Часть CE перемещается. Поиск различных вариантов осуществляется путем изменения направлений передвижения части СЕ (влево, вправо, вверх, вниз, вперед, назад).
4. (Вращение) Часть СЕ или ½ СЕ поварачивается на угол, например 45 °, 90 ° и 180 ° (3 варианта).
5. (САD функции) Над всей (частью, 1/2) СЕ осуществляется некоторая основная функция CAD для построения объекта.
6. (Неясность) Выходная СЕ представляется в неполном виде, напр. отсутствует какая- либо (несколько) деталь, отсуствует необходимая проекция, в т.ч. и главная, отсуствует и полный список составных частей, отсуствует некоторые деталей и т.д. Задачей является в создании функционирующей СЕ в заданных условиях.
7. (Ошибка). Допускание ошибки (ошибок) в выходной СЕ, например, отсутствует штриховка (полностью или частично), изменение штриховки, добавление избыточной линии, удаление существующей линии, смена наименования детали (деталей) и т.д. Принимается, что модель верна.
8. Комбинируются новые решения.
Примечание. Следует считать, что после каждой рекомендации следует текст "При необходимости производятся соответствующие изменения в СЕ с учетом выполнения главной функции изделия и возможности ее сборки разборки."
Пример
См. примеры обсуждаемых (указанных) выше методов геометрических преобразований, а для пункта 7 (изменение штриховки)- рис.4л.
Другой метод контрольных вопросов, связан с поиском вариантов СЕ, дан в [23].
Следует отметить, что некоторые из вышеуказанных методов пересекаются в содержательном смысле.
Некоторые из других методов применения остальных операций приведены ниже:
Замещение - [16].
Модификация - [17].
Трансформация - [17].
Рекурсия - [18].
Неясность- [19-22]
Ошибка - [23].
Инверсия - [24].
Различные геометрические преобразования СE - [1-13].
Под “утверждением” в этой работе понимается объективно существующее отношение, существенное и устойчивое при заданных условиях.
Некоторые из указанные ниже утверждений доказаны в [27,28].
В части утверждений используется понятие эвристической бесконечности [27]. Оно означает совокупность элементов, чье количество является большим числом. Большим числом принимается 100 000.
Утверждение 1 [27]
Варианты СЕ составляют эвристическую бесконечность.
Утверждение 2
Над каждой CE возможно применить геометрические операции для поиска вариантов.
Доказательство
Среди геометрических операций ищутся варианты произвольной выходной CE, которые являются большим числом (Утверждение 1), то есть каждая СЕ обладает вариантами. С другой стороны, любая эвристическая задача может быть решена с помощью многочисленных методов (их количество большое число) [27, утверждение 30]. В данном случае эвристической задачей является "поиск вариантов выходной СЕ."
Утверждение 3
Любая CAD система может быть использована для поиска вариантом CE
Доказательство
Методы, которые были рассмотрены выше, основаны на различных геометрических преобразованиях, например - зеркальное отражение, трансляция, вращение и т.д., а значительная часть из возможных геометрических преобразований имеется в арсенале каждой САD системы (Mirror, Move, Rotate и т.д.). Так как определение варианта СЕ является эвристической задачей, то каждое формализованное геометрическое преобразование может служить основанием для конкретизации пути решения задачи конструктором.
Утверждение 4
В каждом методе геометрических преобразований могут быть применены операции модификация и трансформация в целях получения вариантов этого метода (алгоритмы обеих операций даны в [27]).
Доказательство
Операции модификация и трансформация относятся к эвристическим задачам, эвристическим методам, эвристическим идеям и техническим объектом [27]. Как уже отмечено, рассматриваемые выше методы геометрических преобразований, являются так же эвристическим методом и поэтому обе операции применимы и к ним.
Утверждение 5 [28]
Каждая CE и каждый из ее вариантов обладают недостатками.
Утверждение 6 [28]
Для каждой CE и каждого из ее вариантов существует более лучшее решение.
Так как методы реализации операций являются эвристическими, то к ним относятся утверждения для эвристических методов, доказанных в более общем виде в [27]. Последние приведены ниже.
Утверждение 7
Методы поиска вариантов СЕ составляют эвристическую бесконечность.
Утверждение 8
Количество методов поиска вариантов СЕ непрерывно увеличивается во времени.
Утверждение 9
Каждый из эвристических методов может быть использован для развития самого себя.
Утверждение 10
Каждый эвристический метод может быть модифицирован.
Утверждение 11
Невозможно создание единного общезначимого эвристического метода, с помощью которого могли быть получены все возможные варианты CE.
Возможными ситуациями для продуктивного применением геометрических преобразований СЕ являются:
В докладе разработана систематизация геометрических преобразований (операций) любой исходной СЕ и предложены (или указаны в литературе) методы их практической реализации. Приведены источники , содержащие более подробное их изложение.
Особенностью предложенных методов является то, что некоторая часть из них может быть формально осуществлена с помощью САD системы. Следует подчеркнуть, что предлагаемые алгоритмы являются эвристическими, т.е. набор шагов, которые направляют и подсказывают путь решения, хотя само решение принимается человеком, поставившем перед собой эвристическую задачу "поиска новых вариантов исходной CE".
Операциями являются и присвоение наименований мегаметодам, потому что для каждой операции возможно получение множество конкретных методов ее приложения.
Предложенные методы позволяют систематический поиск вариантов СЕ. Они могут быть использованы как в инженерной практике, так и при обучении студентов инженерных специальностей.
1. Лепаров М.Н. По въпроса за модификации на сглобена единица, научно-техн.конф. с межд. участие “Бъдещето на автоматизацията на дискретното производство”, С., 1997.
2. Лепаров М.Н. Някои методи за модификации на сглобена единица, ІХ научно-техн.конф. с межд. участие “Автоматизация на дискретното производство”, С., 1998.
3. Leparov M.N. Modification of Mechanical Assemblies, “Mechanics in Design’98” Conference, The Nothingham Trent University, UK,1998.
4. Лепаров М.Н., С.И. Калчева. Някои методи за търсене на варианти на сглобени единици, научна сесия’99 с межд. участие на Русенски университет “Ангел Кънчев”, 1999.
5. Лепаров М.Н. Варианти на сглобена единица, десета нац. научно-техн.конф. с межд. участие “Автоматизация на дискретното производство АДП 2000”, Созопол, 2000.
6. Лепаров М.Н. За връзката между евристика и автоматизирано проектиране, научно-техн.семинар “CAD/CAM/CAE системите: теория и практика”, НТС по машиностроене, С., 2001.
7. Leparov M., G.Dinev. About Modification of Mechanical Transmissions , Scientific Conference Research and Development of Mechanical Elements and Systems, IQMES-2002, Srpsko Sarajevo, Republika srpska, 2002.
8. Leparov M., G. Dinev About Formalization in Searching for Versions of Assembled Units, 3- th International Conference “Research and Development in Mechanical Industry”, RaDMI 2003, Herceg Novi, Montenegro Adriatic, 2003.
9. Лепаров М. Трансформации на реално изделие, VІ межд. симпозиум “Техномат и Инфотел’ 2004 Материали, методи и технологии “ Бургас, 2004.
10. Leparov M., G.Dinev On the Issue of Transformation of a Real Product, Conference with Intern. Participation “Research and Development of Machine Elements and Systems”, IRMES’04, Kragujevac, Serbia & Montenegro, 2004.
11. Leparov M., G. Dinev About the Transformations of a Real Product, DEMI 2005, 7 –th international conference on accomplishments of electrical and mechanical industries, Banjaluka, Republic of Srpska, 2005.
12. Leparov M., G.Dinev About Some Methods for Search of Variants of Assembly Unit, Conference with Intern. Participation “Research and Development of Machine Elements and Systems”, IRMES’06, BanjaLuka-Mrakovica, republic of Srpska, 2006.
13. Лепаров М.Н. Някои начини за търсене на трансформации на сглобена единица, ІХ межд. симпозиум “Техномат и Инфотел’ 2007 Материали, методи и технологии“ Бургас, 2007.
14. Dinev G, М. Leparov, M. Vicheva About search of variants of product with CAD, The 5 th Intern.Simp. “Shape, Mechanical and Industrial Design of Products in Mechanical Engineering 2008”, the Faculty of Technical Sciences, Novi Sad, Serbia, 2008.
15. Лепаров М., Вичева М., Георгиев М. Основи на инженерното проектиране, Софттрейд, С., 2015.
16. Лепаров М. Мегаметод „Взаимствуване” за проектиране на техническите обекти, Сборник доклади от межд. научна конф. "Техника, технологии, образование" ICTTE 2014, Ямбол, 2014.
17. Лепаров М.Н. Операции над евристични задачи, методи, идеи и технически обекти, Българско списание за инженерно проектиране, 2014, №23.
18. Лепаров М. Рекурсия на технически обекти, Сборник доклади от ХХІ международна научно-техн. конф. „Автоматизация на дискретното производство” АДП 2012, Созопол, 2012.
19. Лепаров М.Н. Метод „Неяснота” за решаване на евристични задачи, 16 нац. научно-техн. конф. с межд. участие „Автоматизация на дискретното производство” АДП 2007, Семково., 2007.
20. Лепаров М.Н. Относно метода “Неяснота” за решаване на евристични задачи, межд. научна конференция на Технически университет- Габрово „УНИТЕХ’ 07”, Габрово, 2007.
21. Leparov M., G. Dinev About the Heuristic Method of “Vagueness” Appropriated for Solving of Technical Issues, The 5-th International Symposium “Shape, Mechanical and Industrial Design of Products in Mechanical Ingineering 2008”, NoviSad, Serbia and Montenegro, 2008.
22. Leparov M., G. Dinev Heurestic Method “Unclear” for Solve of Technical Problems, Machine Design, Monograph on the Occasion of the 48-th Anniversary of the Faculty of Technical Sciences, NoviSad, Serbia and Montenegro, 2008.
23. Лепаров М. По въпроса за начини за търсене на варианти на сглобена единица, ХІ межд. симпозиум „Техномат и Инфотел’ 2009 Материали, методи и технологии” Бургас, 2009.
24. Лепаров М. Инверсия на технически обекти, Сборник доклади от ХХІІІ международна научно-техн. конф. „Автоматизация на дискретното производство” АДП 2014, Созопол, 2014.
25. Половинкин А. Основы инженерного творчества, изд. Лань, С-Петербург, 2007.
26. Техническое творчество: теория, методология, практика, энцикл. словарь- справочник под ред. А.И Половинкина и В.В.Попова, Научно- произв. объединение „Информ- система”, М., 1995.
27. Лепаров М. Твърдения в теорията на евристичното проектиране, Българско списание за инженерно проектиране, брой 5, 2010.
28. Лепаров М. Някои основни твърдения за процеса на проектиране на технически обекти, Сборник доклади от ХХІ международна научно-техн. конф. „Автоматизация на дискретното производство” АДП 2012, Созопол, 2012.
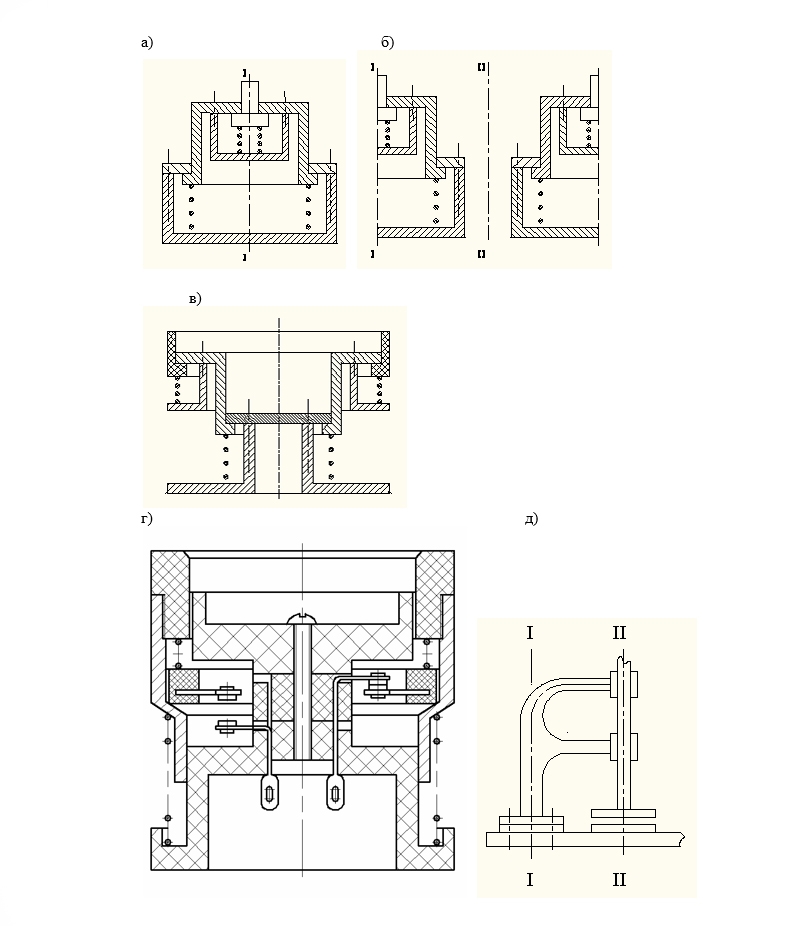
Три примера (а-в; г,д) применения алгоритма метода "Трансляции оси"
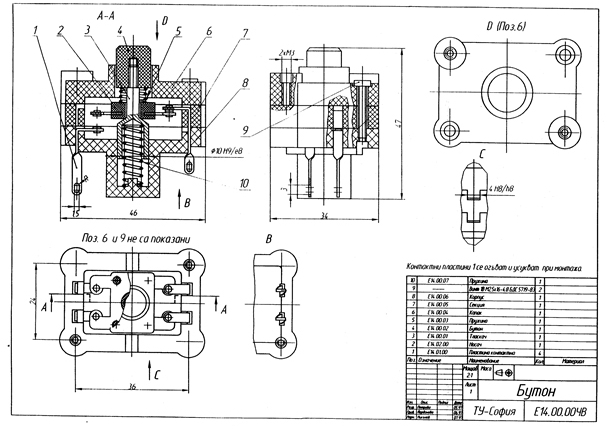
Исходная СЕ относится к примеру рассмотреному на рис.1г
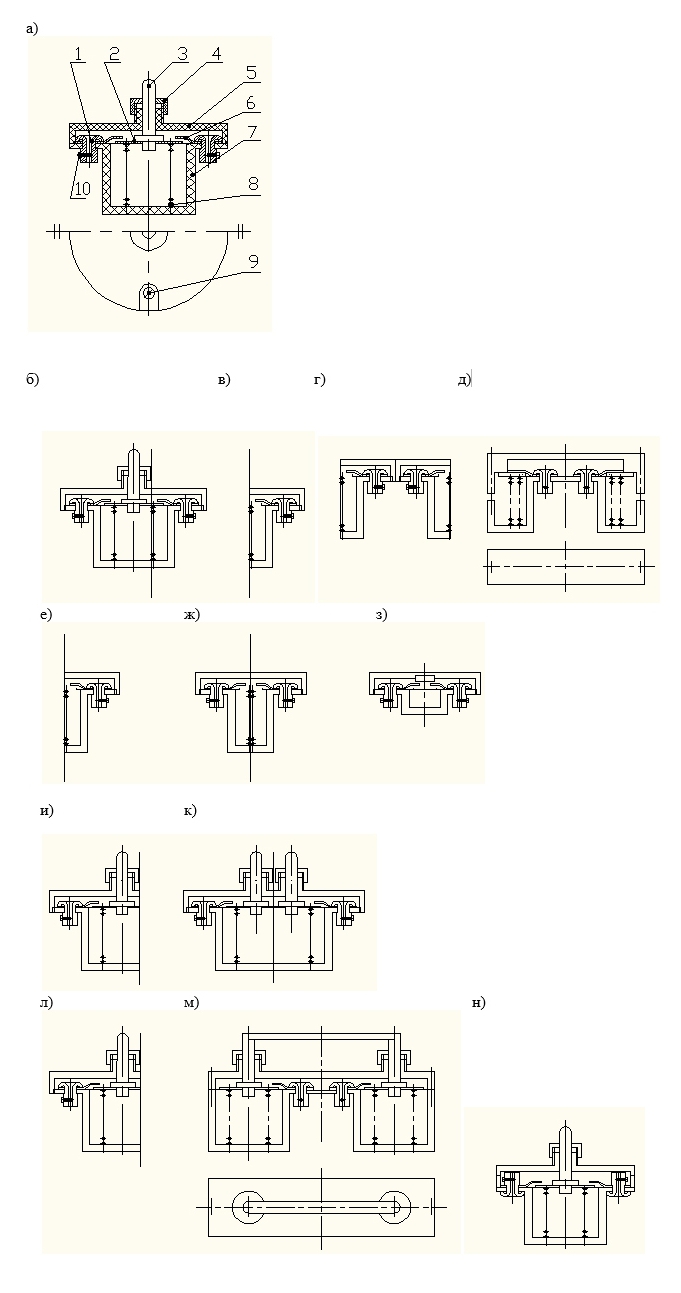
Применение алгоритма метода „Симметрии”
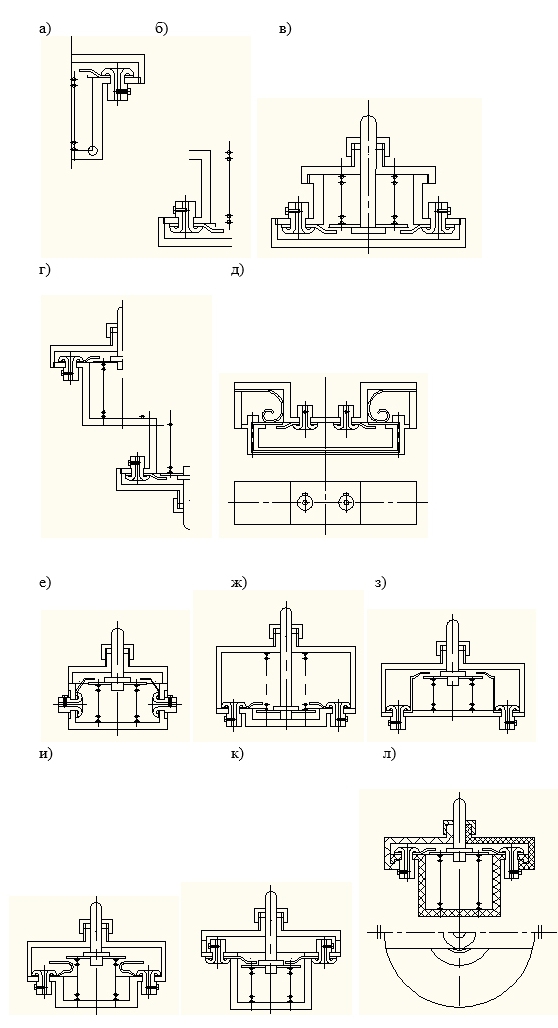
Примеры использования алгоритмов методов " Выворот наизнанку" (а-д), "САD" (е-к) и "Контрольные вопросы" (л)

Ракитская Мария Валентиновна (9 марта 2016 г. 20:19) |
Здравствуйте, Михаил Николаевич! Спасибо за интереснейший доклад! При создании новых конструкций из старой часто встает проблема сравнительной оценки вариантов и проверки работоспособности новой конструкции. Какие критерии при этом использовать? С уважением к Вам, М.В.Ракитская. |

Лепаров Михаил Николаевич (10 марта 2016 г. 3:05) |
Здравствуйте, Мария Валентиновна! Спасибо!
Самое лучшие: провести необходимые расчеты новового варианта, а сравнение два варианта, отвечающие ТЗ проводит с помощью многокритериальную оптимизацию по предварительно принятые критерии, обычно из ТЗ.
Пожалуйста, извините мой русский. С уважением млепаров P.S. Надеюсь Вы заметили идеи в „Сальников Е. М. 3D рисунок как способ построения наглядного изображения”. |