ГЕОМЕТРИЧЕСКАЯ ТОЧНОСТЬ КОМПЬЮТЕРНЫХ АЛГОРИТМОВ КОНСТРУКТИВНЫХ ЗАДАЧ

Рассмотрен критерий геометрической точности (ГТ) алгоритмов, предназначенных для решения задач конструктивной геометрии. Действующий в начертательной геометрии критерий ГТ требует применения циркуля и линейки. Дан исторический обзор формирования этого критерия как абстрактной точности, не отвечающей современным требованиям прикладных задач. Предложено определять реальную ГТ, количественно оцениваемую по погрешности решения. Рассмотрена реальная ГТ компьютерных алгоритмов. Разработан ряд тестов для ее оценки и приведены результаты тестирования. Рассмотрена историческая задача Ферма о сферах. На ее примере дана сравнительная оценка методов НГ, 3D и параметризации. Показано, что требование абстрактной ГТ (циркуля и линейки) сдерживает развитие учебного процесса.

Введение

Критерий геометрической точности активно применяется в дискуссиях между сторонниками начертательной геометрии (НГ)  и сторонниками современных методов геометрического 3D моделирования  [1–3]. Сторонники НГ в своих работах подчеркивают, что решение, полученное ими, является геометрически точным, т.к.  доведено до операций с  циркулем и линейкой. Современному инструменту геометрического моделирования: компьютеру с графическим пакетом САПР – они высказывают недоверие, поскольку им непонятно, как он работает. То есть, как работает циркуль – понятно, а процессы в компьютере непонятны. Поэтому решение, сведенное к  операциям с циркулем и линейкой, геометрически точное, а решение, полученное компьютерными вычислениями – сомнительно и геометрически не точное. Сторонники 3D указывают на высокую точность и эффективность компьютерных построений как основу и перспективу их применения в учебном процессе кафедр графики, современную альтернативу НГ.

Действительно, как работает компьютер, нам непонятно. Но мы им успешно пользуемся. Мы также успешно пользуемся своими евро автомобилями, когда большинство из нас не знает его устройство.

Аргументы о том, что над графическими пакетами работают “серьезные” фирмы [4], что в этих пакетах  как показатель точности вычислений указан восьмой знак после запятой, НГ-оппонентам недостаточно. "Не верим", поскольку в компьютерных расчетах участвуют сплайны и итерации, являющиеся объектами приближенного построения [3]. Построения, выполненные даже кривым циркулем и линейкой, да и тупым карандашом – принимаются ими как геометрически точные, поскольку понятны.

Наряду с этим сторонники НГ активно применяют и, видимо, считают точными 2D построения на компьютере,  выполненные компьютерным циркулем и компьютерной линейкой.  Это выглядит противоречиво, поскольку как компьютер строит окружность и прямую, тоже неизвестно. Однако здесь ему доверяют, решают задачи НГ  и разрешают студентам их применять. Применять 3D студентам, зачастую, не разрешают (чтобы не отвлекались от алгоритмов НГ циркуля и линейки).  

В связи с этим очевидно, что в дискуссии о геометрической точности речь идет не о точности геометрических построений в ее прямом понимании, а об отношении к применению 3D технологий в учебном процессе кафедр графики. Недоверие к компьютерной геометрической точности сторонники НГ используют как аргумент против активного перехода к 3D методам в учебном процессе.  

Фактически вопрос о геометрической точности сводится к педагогической проблеме. Сторонники НГ считают, что доведение алгоритма до циркуля и линейки неизбежно приводит к пониманию студентом геометрической сущности задачи, тогда как компьютерные алгоритмы ее скрывают и приводят к “американизации” образования [2]. Они также утверждают, что компьютерные алгоритмы предназначены лишь для достижения результата, но не для учебного процесса [3]. С этим нельзя согласиться.

Цель нашей работы: краткий исторический обзор вопроса о геометрической точности, оценка геометрической точности компьютерных 2D и 3D алгоритмов, оценка негативной роли алгоритмов “циркуля и линейки” в современном учебном процессе.

1. Исторический обзор вопроса об абстрактной и реальной точности конструктивных задач

Здравый смысл подразумевает под геометрической точностью конструктивной задачи соответствие полученного результата некоторому контрольному достоверному значению. Поскольку это значение заранее не известно (иначе, зачем решать задачу), то остается точность оценить косвенно, по точности применяемого в построениях инструмента. Обратимся к классикам.

Конструктивная геометрия рассматривает решение прикладных задач геометрического моделирования геометрическими построениями в отличие от задач аналитических. Причем, речь идет о задачах, в которых требуется получить прикладной результат. По определению Н.Ф. Четверухина [5, с. 6] в задачах конструктивной геометрии необходимо “не просто убедиться в существовании решения”, а следует стремиться “с помощью своих инструментов фактически осуществить на чертеже построение искомой фигуры”. И далее: “Сама постановка задач, возможность их решения существенно зависит от состава инструментария, который может быть использован чертежником для выполнения построений”.

Исторически инструментом геометрических построений были циркуль и линейка. Именно этим объясняется тот факт, что НГ, являющаяся разделом конструктивной геометрии, признает только эти инструменты как основу для достижения геометрической точности построений, а результат, полученный этими инструментами – единственно геометрически точным. В эпоху Гаспара Монжа других инструментов для геометрических построений не было. (Если бы они были, в частности, инструменты для прямых 3d построений, то, возможно, не возникла и НГ. См. официальную оценку роли Г. Монжа, высказанную в год его юбилея [3,6,7]). В основополагающих работах А. Адлера и Я. Штейнера [8, с. 199] отмечено, что связь геометрической точности с “циркулем и линейкой” восходит к древности (Греция), когда “считали построение выполненным, коль скоро было показано, каким образом оно может быть сведено к …циркулю и линейке, само же построение вовсе не выполнялось. Поэтому простота и точность геометрического решения не играли никакой роли”. Однако, см. там же, “выполнение построений в действительности, то есть с инструментами в руке, есть нечто совсем отличное от выполнения их…с помощью языка”.

Другими словами, задачей конструктивной геометрии является достижение реальной точности имеющимся инструментом, и уже классиками реальная точность метода “циркуля и линейки” считалась сомнительной ввиду погрешностей инструментов и выполняемых ими построений. Эта некая абстрактная логическая точность, достигаемая идеальными инструментами.

Вопросам реальной точности геометрических построений посвящено множество работ, которые “восходят” к началу 19 века. Отметим доступные работы [9–12], в которых математически и экспериментально обоснованы рекомендации затачивать карандаш, не искать пересечение прямых, близких к параллельным. Рекомендовано для решения метрических задач применять замену плоскостей проекций вместо построения перпендикулярных прямых и плоскостей и др. Сегодня эти рекомендации либо забыты, либо нереальны. Добиться качественной графики от нынешних студентов очень сложно, да и не все преподаватели понимают, что нельзя строить точку на конусе с помощью образующей, близкой к его оси. Замену плоскостей часто запрещают, чтобы студенты применяли построение перпендикулярных прямых и плоскостей и т.д.

2. Тестирование реальной точности компьютерных алгоритмов

Точность построений удобнее характеризовать их погрешностью. Так, погрешность 10^-4 означает вероятную ошибку в четвертом знаке после запятой (ПЗ). В своих работах, например [13–16] , мы постоянно оценивали абсолютную погрешность компьютерных 3D построений и приводили, что в зависимости от решаемой задачи она находится на уровне 10^-4…10^-8. Сейчас, в соответствии с целью работы, дополнительно оценим погрешность построений на специально подобранных тестах. Тестирование предполагает заранее известный ответ, с которым можно сравнить результат построений. Оценим погрешности построений на примерах характерных задач из курса НГ, применительно к которым ответ известен качественно или даже количественно.

 Нами разработан набор тестов, позволяющий всесторонне "проверить" графический редактор, часть тестов приведена ниже. Тестирование выполнено в пакете AutoCAD, но результаты могут быть повторены и в других пакетах САПР, применяемых в учебном процессе кафедр графики (SolidWorks, Inventor, Компас). Все построения выполняются с объектными привязками или с применением параметризации [16].

2.1. Изометрия куба

Рассмотрим задачу о проекции куба на плоскость, перпендикулярную одной из его диагоналей (рис. 1, а). Известно, что проекция представляет собой правильный шестиугольник. Вывод сделан И. Кеплером (1619 г.) и А. Фрезье (1738 г.) [17,18]. Это ортогональная изометрия. В AutoCAD’е предусмотрено построение четырех изометрий, по количеству диагоналей куба. Цель данного теста – проверить, насколько изометрия куба, создаваемая AutoCAD’ом, является правильным шестиугольником.

Построим куб (команда Box) с произвольной длиной стороны. Построим одну из его ортогональных изометрий. Спроецируем куб (команда Solprof или Flatshot) на плоскость экрана. Зададим точность (Units) до восьмого знака ПЗ. Измерим (List) длины всех 12-ти отрезков, являющихся проекциями ребер куба. Сравнив между собой полученные значения, убедимся, что длины совпадают до последнего знака. При длине стороны куба 100 все они равны 81.64965809. Это первая качественная проверка. Для второй, количественной проверки, вычислим длину каждого из отрезков. На основе тригонометрических преобразований, вероятно, повторяя выкладки Фрезье, получим, что для куба со стороной a длина  отрезков изометрической проекции определяется формулой: a1 = a sin(arctg (sqrt 2)). При а =100 получим то же значение, что и при измерении графически построенной проекции, равное 81.64965809. Вывод: компьютер выполняет построение изометрии 3d объектов с погрешностью 10^-8.  

2.2. Точность построения коник

В учебном процессе коники выступают как сечения и линии пересечения квадрик, проекции этих линий, очерковые образующие  квадрик. Рассмотрим точность коник согласно их определению как сечений конуса плоскостью.

В AutoCAD’е существуют три  “штатные” квадрики, являющиеся примитивами AutoCAD’а – это конус, сфера, цилиндр.  Для остальных "нештатных" квадрик отсутствуют  специальные команды построения – это гиперболоиды, параболоиды, эллипсоиды, их нужно создавать вращением или перемещением коник.  

То же относится и коникам. Штатные коники – эллипс, окружность.  Для них предусмотрены специальные команды построения. Эти коники  диагностируются качественно, то есть при их указании курсором, выводится имя коники. Гипербола и парабола – нештатные коники. В AutoCAD’е их получают  как сечения конуса, эти объекты формируются как сплайн кривые.

Оценим точность, с которой создаются штатные коники – эллипсы (рис. 1, б). Для этого проверим выполнение его определяющего свойства: эллипс как геометрическое множество точек (ГМТ), сумма расстояний которых до точек фокуса является постоянной. Строим произвольный эллипс e. С помощью окружности находим точки фокусов F и F*. Назначаем две произвольные точки эллипса  A,B. Соединяем их отрезками с точками  фокусов.  Строим отрезки F*A* и FB*, длины которых равны сумме расстояний от точек A,B до фокусов. Измерениями убеждаемся,  что длины совпадают до восьмого знака ПЗ. Это указывает, что эллипс (и окружность) воспроизводятся с погрешностью не более 10^-8.

Для оценки точности нештатных коник построим гиперболу h (рис. 1, в) как сечение кругового конуса плоскостью α. Для построения асимптот гиперболы n, m построим сечение β||α и переместим его в плоскость α в центр гиперболы: 1→ 4.  В плоскости α строим ось гиперболы i (4-5), отрезок d, пепендикулярный i, находим точку 7, с помощью окружности c находим фокусы гиперболы F, F ′. 

Точность гиперболы определим, учитывая, что она является ГМТ, для которых разность расстояний до точек фокуса является постоянной, равной расстоянию между вершинами гиперболы, точки 2,3. Задаем произвольную точку A гиперболы h, строим отрезок AF ′, с помощью окружности c′ определяем точку 8=c′∩AF′. Измерив длины отрезков (2,3) и (8, F′), убеждаемся, что они равны с точностью до восьмого знака ПЗ. 

Параболу p (рис. 1, г) также строим как сечение кругового конуса плоскостью. По средней точке параболы находим ее вершину V. Строим ось параболы i (1-V).  Для нахождения фокуса F реализуем оптические свойства параболы. Из произвольной точки 2 оси i строим отрезок (2,3), касательный к параболе. Точку 3 касания определяем объектной привязкой. Строим отрезок m, симметричный i относительно (2,3), и отрезок m′ ||m.  Находим фокус параболы F = m′ ∩ i и директрису d.

Точность параболы оцениваем, исходя из ее определения как ГМТ, равноудаленных от фокуса и директрисы. Назначаем произвольную точку А параболы.  Строим отрезки AF и AB и измеряем их длину. Убеждаемся, что длины совпадают до восьмого знака ПЗ. 

Гипербола и парабола как сечения квадрик и как объекты AutoCAD’а представляет собой плоские сплайны. Эту характеристику (Properties: Planar) можно прочесть по команде List. Приведенным тестированием показано, что погрешность построения таких сплайнов находится на уровне 10^-8 .

2.3.Точность построения линий пересечения

Приведем примеры тестирования, основанные на оценке точности коник, образующихся в частных случаях пересечения квадрик [19]. При тестировании важно обеспечить точность реализации частного случая. Например (рис. 1, д), построить круговой конус, создать его дубликат и повернуть вокруг произвольной точки оси. Реализуется теорема Монжа. В зависимости от значений угла α в пересечении конусов образуются эллипсы, параболы, гиперболы в различном сочетании. В приведенном примере возникли эллипс и парабола. 

Необходимо различать взаимное пересечение штатных квадрик и пересечение, в котором хотя бы одна квадрика нештатная. В первом случае образуются штатные коники (эллипс, окружности) и плоские сплайны (гипербола, парабола). Штатные коники диагностируются качественно. Их погрешность, как показано выше, находится на уровне 10^-8. Погрешность гипербол и парабол была проверена приведенными выше методами (см. рис. 1, б, в). Она составляет 10^-5 …10^-8.

При пересечении нештатных квадрик коники реализуются как неплоские сплайны (Non-Planar). Примером (рис. 1, е) является пересечение двух однополостных гиперболоидов вращения (ОГВ), имеющих общую вписанную сферу. Очерковую гиперболу ОГВ получим как сечение кругового конуса, сам ОГВ – ее вращением вокруг мнимой оси. Модель пересечения получим поворотом дубликата гиперболоида вокруг некоторой точки его оси, желательно точки центра очерковой гиперболы. В приведенном примере в пересечении возникли эллипс и гипербола (рис. 1, ж).

Для исследования линию пересечения копируем. Установим плоскость построений по трем каким-либо точкам сплайна. Командой List выводим координаты остальных точек и по z-координате определяем их отклонение от плоскости. Депланация не превышает 10^-4.  Последующая проверка коник,  выполненная по методам (см. рис. 1, б – г), показывает погрешность на уровне 10^-4…10^-6.

2.4. Оценка коник на основе теоремы Паскаля

Теорема Паскаля (1623—1662) – одна из основных теорем проективной геометрии [20]. Применим ее для оценки точности коник как линий пересечения. На тестируемой конике задаем шесть произвольных точек и произвольно их нумеруем 1…6 (рис. 1, ж). Соединяем точки отрезками прямых (Line) по порядку принятой нумерации, то есть в последовательности 1-2-3-4-5-6-1. Последний отрезок 6-1 замыкает ломаную линию, образуя шестиугольник Паскаля. Для каждого варианта нумерации образуется свой шестиугольник. При простановке точек их расположение не должно быть симметричным. Находим три точки пересечения следующих пар отрезков: А=(1-2)∩(4-5); B= (2-3) ∩ (5-6); C=(3-4) ∩(6-1). Указанные точки могут находиться как на пересечении отрезков, так и на их продолжении.

Согласно теореме Паскаля, если линия является коникой, то точки A,B,C принадлежат одной прямой. Для проверки этого положения задаем (Units) предельную точность измерения углов, то есть до восьмого знака ПЗ. Устанавливаем плоскость измерений в плоскость тестируемой коники. Определяем (List) угол между отрезками AC и BC (угол Паскаля). Предварительно рекомендуем тестировать какой-либо штатный эллипс и убедиться, что для него измеряемый угол с предельной точностью равен 0⁰ или 180⁰.

Угол Паскаля весьма чувствителен к отклонению формы кривой от коники. Так, смещение осей ОГВ в примере (см. рис. 1, е) на 1%, то есть отклонение от теоремы Монжа, приводит к увеличению угла Паскаля в 1000 раз. Проведенный эксперимент, и другие аналогичные ему, позволили считать величину 10^-3 градуса как граничное значение угла Паскаля. При меньших значениях этого угла проверяемая линия уверенно может рассматриваться как коника. 

В рассмотренных нами примерах угол Паскаля не превысил 10^-5, что указывает на высокую точность компьютерных построений. Например, для гиперболы (см. рис. 1, ж), возникшей при пересечении гиперболоидов (см. рис. 1, е), угол составил   10^-5…10^-6 градуса в зависимости от расположения и нумерации вершин шестиугольника Паскаля. 

2.5. Точность проецирования линий пересечения

Известно, что при наличии общей плоскости симметрии квадрик линия их пересечения на эту плоскость проецируется в конику [19]. Воспользуемся этим свойством для оценки точности построения линии пересечения и ее проецирования.

Тестирование выполнено на примере  пересечения эллиптического конуса и сферы (рис. 1, з), которые являются штатными квадриками. Положение квадрик характеризуется фронтальной α и профильной β плоскостями симметрии. Линия пересечения – пространственная кривая 4-ого порядка, содержащая ветви m,n. Ее фронтальной проекцией является эллипс e, профильной – гипербола h. Как объекты AutoCAD’а эти линии представляют собой плоские сплайны.

Оценка точности компьютерных построений была выполнена по шестиугольнику Паскаля. Для эллипса угол Паскаля составил 0.00002338⁰, для гиперболы 0.00005650⁰, что указывает на высокую точность построений.

Отсутствие горизонтальной плоскости симметрии квадрик приводит к тому, что кривые m₁, n₁ горизонтальной проекции линии пересечения существенно отличаются от эллипса, несмотря на кажущееся с ним сходство. Угол Паскаля для этих кривых составил соответственно  0.031907 и 0.033258, то есть в 10 раз превысил указанный выше пороговый уровень. 

2.6. Прямые линии в пересечении квадрик

При распадении линии пересечения квадрик возможно образование прямых линий в пересечении [19]. Предельным случаем является распадение на четыре прямые. Рассмотрим два примера такого распадения и оценим точность компьютерных построений по точности образующихся прямых.

 Четыре отрезка прямых образуются при пересечении двух эллиптических конусов с общей вершиной (рис. 1, и). Построим конусы как штатные квадрики, объединим их и извлечем линии пересечения. Диагностирование (List) показывает, что это объекты Line, то есть предельно точно построенные отрезки прямых линий. Погрешность их построения, как и для всех качественно диагностируемых объектов, находится на уровне 10^-8.

Второй пример – пересечение по четырем прямым двух нештатных квадрик – ОГВ (рис. 1, к). Для возникновения прямых линий оси гиперболоидов должны пересекаться, очерковые гиперболы и угол между осями гиперболоидов должны  быть прямыми. Образуются две пары пересекающихся отрезков прямых: m∩n и m'∩n ', причем m||m', n||n'. Командой List определяем, что прямые созданы как сплайны. Установив ПСК осью Х вдоль любого из полученных отрезков, в диагностическом сообщении видим, что отклонение сплайнов от прямой наблюдается на уровне 10^-7.

Таким образом, прямые линии, возникающие при пересечении штатных квадрик, создаются с погрешностью на уровне 10^-8. При нештатных квадриках в качестве прямых образуются сплайны, воспроизводящие прямые линии с точностью 10^-7…10^-8. 

2.7. Дополнительные данные по тестированию компьютерной точности 

Приведенные выше тесты легко воспроизвести и убедиться в приведенных нами  оценках точности компьютерных построений. Дополнительно отметим наши работы, в которых рассмотрены более сложные частные случаи пересечения квадрик: гиперболоидов с параболоидами [21], софокусных и псевдософокусных квадрик [14]. Рассмотрена  оценка точности частных случаев пересечения торов: образование кругов Вилларсо и коник в проекции пересекающихся торов с общей экваториальной плоскостью [22].   Во  всех примерах показано, что погрешность построений не выше 10^-4.

Для поверхностей, получаемых сдвигом контура по траектории (Sweep), погрешность была исследована при построении геометрически точных моделей резьбы, зубчатых и червячных передач, а также червячной фрезы [16]. Показано, что их погрешность не превышает 10^-4. 

 Для наиболее сложных поверхностей, создаваемых “натягиванием” сплайна на каркас (Loft),  погрешность зависит от плотности и точности каркаса. Характерная зависимость погрешности от плотности рассмотрена в работе [23]. 

3.  О негативной роли “циркуля и линейки” в учебном процессе

Методы 3D активно внедряются в практику, делая ненужными 2D проекционные преобразования и НГ как их теоретическую основу. Ввиду эффективности 3D методов сложные задачи курса НГ являются простыми и даже элементарными для новых методов [24, 25]. Сейчас, в соответствии с темой доклада,  покажем, что стремление ограничить алгоритмы геометрического моделирования применением “циркуля и линейки” с целью достижения “геометрической точности” негативно влияет на учебный процесс, сдерживая его развитие.

Рассмотрим знаменитую историческую задачу П. Ферма о сферах (1640 г.): построить сферу, касательную к четырем заданным сферам S₁ – S₄ (рис 2, а). Решение приведем обзорно. Подробное изложение и наша реализация основных алгоритмов этой задачи переданы к публикации. 

3.1. Геометрическая модель задачи Ферма о сферах

Возможны два варианта касания двух сфер: внешнее – сферы расположены снаружи относительно друг друга и внутреннее, при котором  одна из сфер расположена внутри другой. Из этого следует, что максимальное количество решений задачи Ферма равно количеству комбинаций из четырех элементов, каждый из которых может иметь два значения, то есть 4²=16. В зависимости от положения сфер часть решений может отсутствовать или задача может не иметь решения.

За основу нашего решения возьмем  алгоритм [26, с. 97], [27] и покажем его реализацию различными компьютерными методами: компьютерные “циркуль и линейка” как метод НГ, 3D методы и 3D параметризация.

ГМТочек, равноудаленных от двух сфер, является одна из чаш двуполостного гиперболоида вращения (ДГВ) (рис. 2, б). Из четырех сфер можно составить шесть пар. Экспериментально установлено, что шесть чаш ДГВ пересекаются в одной  точке, которая и является центром искомой касательной сферы (теоретическое обоснование этого вывода нам неизвестно). Поэтому для решения достаточно построить чаши ДГВ трех произвольно выбранных пар сфер и найти их общую точку (рис. 2, в). 

Составим три пары сфер. Для метода НГ (см. ниже) необходимо, чтобы в каждой паре была общая сфера. Это приведет к софокусному пересечению ДГВ и связанному с этим существенному упрощению решения, поскольку в пересечении образуются коники [14, 26]. Для метода 3D подбор пар не имеет значения. 

 Для каждой пары сфер решаем планиметрическую задачу по определению гиперболы как очерка ДГВ (рис. 2, г).  Строим окружности с, с* сечений сфер выбранной пары некоторой единой плоскостью. В ней найдем  ГМТ, равноудаленных от этих окружностей. Точки этого множества можно построить, как центры окружностей различного радиуса, касательных  к   с, с*. Необходимо учесть условие касания искомой сферы с заданными. В приведенном примере ветвь h гиперболы получена при внутреннем касании со сферой, имеющей сечением окружность с,  и внешнем касании - с окружностью  с*.  Ветвь той же гиперболы h′ соответствует противоположным условиям касания, то есть внешнему касанию с окружностью c и внутреннему –  с окружностью с*.  Центры окружностей, точки F, F*, являются точками фокусов найденной гиперболы h, h′.

Для точного построения гиперболы достаточно найти пять ее точек, например, точки 1–5. Затем по ним построить сплайн-кривую, применив Lisp-программу [28] или параметризацию [16]. Такая гипербола формируется “выходом в пространство” как результат сечения штатного конуса и обладает погрешностью 10^-8.  Построение сплайн-кривой “вручную”, даже по 10 – 15 точкам, приводит к значительному увеличению погрешности до 10^-2..10^-3. 

3.2. Алгоритм  НГ

Решение, приведенное авторами алгоритма [26] крайне ненаглядно и громоздко. Рассмотрим наше решение, которое также является весьма громоздким, но выполнено в соответствии с программой курса НГ.

Составим две тройки сфер. Первая S₁,S₂,S₄, вторая S₁,S₃,S₄. В первой тройке рассмотрим два ДГВ: для сфер S₁, S₂ и для сфер S₁,S₄. Наличие общей сферы S₁ приводит к тому, что эти ДГВ являются софокусными и пересекаются по гиперболе h(1,2,4). Параметры в обозначениях гипербол и ДГВ обозначают номера сфер, для которых они построены.  ДГВ второй тройки, имеющей ту же общую сферу S₁, пересекаются по гиперболе h(1,3,4). Центр искомой общей касательной сферы S, точку O, определяем как точку пересечения  гиперболы h(1,3,4) и плоскости Δ, в которой расположена гипербола h(1,2,4). Саму гиперболу h(1,2,4) строить не будем, найдем лишь ее три точки.

Уточним условия задачи. Пусть искомая сфера S имеет внутреннее касание с S₁, S₂ (то есть эти сферы расположены внутри S) и внешнее – со сферами S₃, S₄.

Строим фронтальную и горизонтальную проекции заданных сфер (рис. 2, д). Находим плоскость Δ. Для этого преобразуем чертеж так, чтобы плоскость центров первой тройки сфер стала плоскостью уровня П4. В ней строим софокусные гиперболы  h(1,2) и h(1,4) как очерковые для ДГВ этой тройки. Из-за перегруженности чертежа построение этих гипербол не показано, оно выполнено по алгоритму (см. рис. 2, г). На пересечении гипербол h(1,2) и h(1,4) находим точку 5₄. С помощью концентрической сферы S* с центром в точке 1₄ определяем  точку 6₄. По точкам 5,6 определяем плоскость Δ, перпендикулярную П4, задаем ее двумя отрезками m∩n, которые назначаем в плоскости П5||Δ с учетом наглядности последующих построений.

Для второй тройки сфер чертеж преобразуем так, чтобы плоскость центров ее сфер стала плоскостью уровня П7. В этой плоскости строим софокусные гиперболы  h(1,3) и, повторно, – гиперболу  h(1,4). Указанные гиперболы являются очерковыми для ДГВ второй тройки сфер.  По точкам 8₇, 9₇ определяем плоскость Ω, перпендикулярную П7.  В плоскости П8 || Ω способом концентрических сфер с центром в т. 1₇ строим гиперболу h(1,3,4).

Последовательным преобразованием из П5 находим проекции отрезков m, n в плоскости П7. Находим точки 10,11 отрезка, по которому пересекаются плоскости Δ(m, n) и Ω.  В плоскости П8 находим точку О пересечения отрезка (10,11) с гиперболой h(1,3,4). Она является центром искомой касательной сферы S. Обратным преобразованием находим ее фронтальную О₂ и горизонтальную проекции О₁.

Радиус искомой сферы определяем как истинную величину отрезков, соединяющих точку О с центрами заданных сфер, с добавлением или вычитанием радиусов этих сфер в зависимости от условий касания. Например (рис. 2, е), в плоскости П10 для сферы S₂, имеющей внутреннее касание, к истинной величине отрезка (O,2), добавляем радиус сферы S₂. Точка L является точкой ее касания с искомой сферой. Для сферы S₃, имеющей внешнее касание, определена точка касания М.

3.3. Алгоритм  3D

Произвольно, лишь с учетом наглядности, выбираем три пары сфер для построения трех ДГВ. В нашем примере (см. рис. 2, а) это пары S₁,S₃, S₁,S₄ и S₂,S₃. Для каждой из них строим по одной ветви гиперболы как ГМТ, равноудаленных от очерковых окружностей этих сфер (см. рис. 2, г).

Вращением гипербол строим чаши трех ДГВ (рис. 2, б, в) Н₁₃, Н₁₄, Н₂₃.  Находим точку О пересечение чаш и принимаем ее за центр искомой сферы.

Строим (рис. 3, а) сечения сфер S₁ – S₄ плоскостями, проходящими через центры этих сфер и точку О. По окружностям сечений заданных сфер c₁ – c₄ и окружностям c, c′ сечений найденной сферы   определяем точки K,L,M,N касания сфер.

Длины отрезков, соединяющих точку О с точками касания, определяют радиус искомой сферы S. По центру и радиусу строим искомую общую касательную сферу (рис. 3, а).

3.4. Алгоритм 3d параметризации

Параметризация [29,30]  существенно упрощает решение задачи о сферах. Модель параметризации основана на том, что в точках касания заданных сфер с искомой сферой радиальные отрезки, соединяющие точки касания с центрами сфер, выстраиваются в прямую линию, а для искомой сферы ее четыре радиальных отрезка имеют равную длину, как радиусы этой сферы. В итоге задача сводится к построению стержневой конструкции с заданным положением и размерами стержней.

 Модель 3D параметризации построим в пакете SolidWorks (в AutoCAD’е 3D параметризации пока нет). Строим (рис. 3, б) отрезки AK, BL, CM, DN, в которых точки A,B,C,D являются центрами заданных сфер.   Эти точки фиксируем. На отрезки проставляем управляющие размеры, равные радиусам сфер.  Дополняем конструкцию  отрезками KO, LO, MO, NO, которые играют роль радиусов искомой сферы. Каждой паре отрезков, например, AK и KO, присваиваем коллинеарность, контролируя происходящее при этом их совмещение в прямую линию.

Отрезкам KO, LO, MO, NO присваиваем взаимосвязи равенства. В итоге точка O принимает положение центра искомой общей касательной сферы S5. Проставляя справочный размер, определяем радиус найденной сферы. Точки K,L,M,N принимают положение точек касания. Задача решена. Для наглядности модель дополним построением пяти сфер.

Созданную конструкцию можно быстро перестроить для других условий касания и параметров заданных сфер. Например, для сферы с внешним касанием (рис. 3, в) или внутренним касанием (рис. 3, г) с каждой из заданных сфер.

3.5. Сравнительная оценка алгоритмов

На примере задачи Ферма сравним алгоритмы НГ, 3D и параметризации по критериям геометрической точности, сложности, наглядности и эффективности [24].

В рассмотренной задаче алгоритмы НГ и 3D реализованы единым инструментом – графическим пакетом САПР (AutoCAD), включая единообразное точное построение гипербол [28], которые являются основным источником погрешности. Погрешность оценивали по разбросу значений радиусов касательной сферы, определенных по отношению к каждой из заданных сфер. Простановка контрольных размеров,  (см. рис. 2, e) показала, что при таких условиях сравнения погрешность  алгоритмов НГ и 3D оказалась сопоставимой, на уровне 10^-4.

Значительно более высокая точность (погрешность 10^-8, см. рис. 3, б) достигнута при 3D параметризации. Причина в том, что графические построения гипербол, точек и линий пересечения не входят в алгоритм. Все определяют аналитические методы решения систем уравнений, выполняемые программным обеспечением графического пакета.

Сложность алгоритмов оцениваем по трудозатратам на выполнение построений. Такой подход неизбежно субъективен. По нашему мнению, сравнение построений НГ (см. рис. 2, д) с реализацией различными алгоритмами 3D (рис. 3)  однозначно указывает на преимущества 3D алгоритмов. Вместо сложных, громоздких, многократных преобразований чертежа НГ, нереальных для учебного процесса, видим построения 3D объектов, которые выполняются значительно быстрее применением  простых в освоении команд графического пакета. Наименьшей сложностью обладает алгоритм 3D параметризации, в котором требуется минимум построений.

Сравнение алгоритмов по наглядности решения также не в пользу НГ.  Вместо мало наглядных и сложных для понимания проекций НГ (см. рис. 2, д) имеем  реалистичные виртуальные 3D модели, соответствующие нашему зрительному восприятию.

Под эффективностью алгоритма понимаем широту охвата проблем, связанных с рассматриваемой задачей. Здесь вне конкуренции метод 3D параметризации, позволяющий выполнить исследования геометрической модели с минимальными затратами.

Заключение

Независимо от метода решения: НГ или 3D – залогом успешного решения является  понимание геометрической сущности задачи. Это делает необоснованными опасения в том, что компьютерные методы 3D снижают геометрическую подготовку студентов. Снижается лишь знание методов НГ, но это с лихвой  компенсируется подготовкой по методам 3D.

Компьютерные 3D методы моделирования позволяют в значительной мере “переложить” решение на математическое и программное обеспечение графического пакета САПР. Это позволяет решать значительно более сложные задачи, недоступные методам НГ. Примером тому является рассмотренная задача Ферма о сферах, которая, ввиду сложности нереальна в курсе НГ, но с успехом может быть решена студентами, владеющими 3D методами.

Компьютерные 3D методы, особенно 3D параметризация, позволяют достаточно просто исследовать геометрические закономерности задач. Этим они создают возможности для реализации исследовательских компетенций студентов.

На студентов оказывает влияние и фактор эмоционального восприятия сопоставляемых алгоритмов. Вместо набора множества линий, карандаша и бумаги, которые до сих пор в учебном процессе остаются основными инструментами НГ,  решение 3D – это  современные компьютерные технологии, цвет, фотореалистичность. Все это повышает интерес к учебному процессу.

 Методы 3D лежат в основе современных САПР и активно развиваются. В отличие  от НГ, они являются актуальными и перспективными. Обучение им уже в первом семестре готовит студентов к освоению современных методов проектирования и геометрического моделирования, к последующему курсу инженерной компьютерной графики, к курсовому и дипломному проектированию, делает их востребованными на рынке  труда.  

Выводы

1. Точность геометрических построений необходимо определять не по абстрактным критериям применения циркуля и линейки, а по реальной погрешности построений, которую можно измерить и сравнить с требуемым значением.
2. Предложена методика тестирования реальной точности компьютерных геометрических построений. Результаты тестирования показали, что абсолютная погрешность, зависящая от компьютера как инструмента построений,  не превышает 10^-4, а в большинстве задач находится на уровне 10^-6 –10^-8.

Список литературы

1. Хейфец А.Л. Начертательная геометрия как “бег в мешках” / А.Л. Хейфец // Проблемы качества графической подготовки студентов в техническом вузе. Материалы V Международной научно-практической интернет-конференции. КГП 2015” / А.Л. Хейфец. – Пермь: ПГТУ. 2015. – С. 292–325.

2. Сальков Н.А. Американизация геометрического образования в России и начертательная геометрия / Н. А. Сальков // Геометрия и графика. 2015. Т. 3. №. 3. – C. 38–46.

3. Короткий В.А. Ломоносов и компьютерные технологии в обучении начертательной геометрии / В.А. Короткий, Л.И. Хмарова // Геометрия и графика. – 2015. Т. 3. №. 3. – C. 58–63.

4. Головнин А.А.. Базовые алгоритмы компьютерной графики (что там, за “кнопками”?) / А.А. Головнин // http://dgng.pstu.ru/conf2016/papers/4/

5. Четверухин Н.Ф. Методы геометрических построений / Н.Ф. Четверухин. – М:. Гос. уч. пед. издат. – 1952. – 145 с.

6. Гаспар Монж. Начертательная геометрия. – Изд-во АН СССР, 1947. – 288 с.

7. Каргин Д.И. Гаспар Монж – творец начертательной геометрии / Д.И. Каргин // Гаспар Монж: сборник статей к двухсотлетию со дня рождения. – Изд-во АН СССР, 1947. – C. 17–44.

8. Адлер А. Теория геометрических построений / А. Адлер. – Л.: Учпедгиз, 1940. – 232 с.

9. Николаева Л.П. О точности графических построений / Л.П. Николаева // Вопросы начертательной геометрии и инженерной графики. Научные труды Ташкентского института инж. железнодорожного транспорта. – Ташкент: Изд-во “ФАН”, 1966. Вып. 39. – С. 71–78.

10. Николаев И.Н. К вопросу исследования графических построений / И.Н. Николаев, М.И. Букашкин // Геометрография. Межвузовский научно-методич. сб. – Рига: РПИ. 1974. Вып. 1. – С. 95–100.

11. Николаев И.Н. Отклонения реальных геометрических образов от идеальных в графических построениях / И.Н. Николаев, Ю.И. Гуляев // Геометрография. Межвузовский научно-технич. Сб. – Рига: РПИ. 1977. Вып. 2. – С. 29–39.

12. Бородина Л.Н. Решение метрических задач в начертательной геометрии с учетом точности графических построений / Л.Н. Бородина, А.Ю. Рыченкова // Актуальные проблемы гуманитарных и естественных наук. –2013. – №7-1.

13. Хейфец А.Л. Реализация обобщенной теоремы Данделена для произвольных квадрик вращения в AutoCAD / А.Л. Хейфец, В.Н. Васильева // Геометрия и графика. –2014. Т. 2. №. 2. – C. 9–14.

14. Хейфец А.Л. 3D-модель пересечения софокусных и псевдософокусных квадрик / А.Л. Хейфец // Вестник Южно-Уральского государственного университета. Серия “Компьютерные технологии, управление, радиоэлектроника”. – Челябинск: Изд-во ЮУрГУ. 2013. – Том. 13. №2, – С. 88–96.

15. Хейфец А.Л. 3d-модель червячной фрезы / А.Л. Хейфец // Обработка металлов. Технология. Оборудование. Инструменты. Научно-технический и производственный журнал. – Новосибирск: НГТУ. – 2013. – №3. – С. 47-54.

16. Инженерная 3d-компьютерная графика. Учебник и практикум для академического бакалавриата. / А.Л. Хейфец, А.Н. Логиновский, И.В. Буторина, В.Н. Васильева; под ред. А.Л. Хейфеца. – 3-е изд., пер. и доп. – М.: Изд-во Юрайт, 2015. – 602 с.

17. Баскарев В.А. Значение Ферзье в создании начертательной геометрии / В.А. Баскарев // Начертательная геометрия. Сборник трудов Всесоюзн. заочн. политех. инст-та. Вып. 93. – М. 1974. С. 3–11.

18. Фролов С.А. В поисках начала: Рассказы о начертательной геометрии / С.А. Фролов, М.В. Покровская. – М.: МГТУ, 2008. – 192 с.

19. Начертательная геометрия / Н.Ф. Четверухин, В.С. Левицкий, З.И. Прянишникова и др.; под ред. Н.Ф. Четверухина. – М.: Высш. шк., 1963. – 420 с.

20. Четверухин Н.Ф. Проективная геометрия / Н.Ф. Четверухин. – М: Уч.пед.гиз. – 360 с.

21. Хейфец А.Л. Исследование линии пересечения поверхностей как новый тип позиционных задач в курсе теоретических основ компьютерного геометрического моделирования / А.Л. Хейфец // Проблемы геометрического моделирования в автоматизированном проектировании и производстве. 24-26 июня 2008. Сб. материалов 1-ой международной научной конференции. Москва 2008. Под. ред. В.И. Якунина. – М.: МГИУ. – С. 395-401.

22. Хейфец А.Л. 3D-моделирование линий пересечения поверхностей (AutoCAD) / А.Л. Хейфец, В.Н. Логиновский, И.В. Буторина // Совершенствование подготовки учащихся и студентов в области графики, конструирования и стандартизации. Межвузовский научно-методический сборник. – Саратов: СГТУ. 2004, – С. 127–133.

23. Хейфец А.Л. 3D-модели линейчатых поверхностей с тремя прямолинейными направляющими / А.Л. Хейфец, А.Н. Логиновский // Вестник Южно-Уральского государственного университета. Серия “Строительство и архитектура”. – Челябинск: Изд-во ЮУрГУ. 2008. – Вып. 7. №25(125), – С. 51–56.

24. Хейфец А.Л. Сравнение методов начертательной геометрии и 3D компьютерного геометрического моделирования по точности, сложности и эффективности. – Вестник Южно-Уральского государственного университета. Серия “Строительство и архитектура”. – Челябинск: Изд-во ЮУрГУ, 2015. – Т. 15. №4, – С. 49–63.

25. Логиновский А. Н. Решение задач на основе параметризации в пакете AutoCAD / А.Н. Логиновский, А. Л. Хейфец // Геометрия и графика. – М.: ИНФРА-М. Том. 1. Вып. 2. – C. 58 –62.

26. Чернышова З.Т. К методике решения задач по начертательной геометрии / З.Т. Чернышова, В.В. Глаговский. Изд-во Львовского университета. – 1964. – 105 с.

27. Короткий В.А. Задача Аполлония на экране компьютера / В.А. Короткий, Е.П. Дубовикова // Совершенствование подготовки учащихся и студентов в области графики, конструирования и дизайна. Межвузовский научно-методический сборник. – Саратов, СГТУ. – 2013. – С. 5–9.

28. Короткий В.А. 3D-моделирование коник в пакете AutoCAD / В.А. Короткий, А.Л. Хейфец // Актуальные вопросы графического образования молодежи. Материалы VI Всероссийской научно-методической конференции. Под ред. Ю.П. Шевелева, А.П. Передбогова. – Рыбинск. РГТА, 2005. – С. 102–105.

29. Логиновский А.Н. Комплексные задачи в пакетах среднего САПР / А.Н. Логиновский // Наука ЮУрГУ: материалы 67 научной конференции. Секции технических наук . – Челябинск: Издательский центр ЮУрГУ, 2015. – С. 201–206. [Электронный ресурс]. –http://www.lib.susu.ac.ru/ftd?base=SUSU_KONF&key=000537718_content

30. Хейфец А.Л. Параметризация как средство решения задач 3D компьютерного геометрического моделирования / А.Л. Хейфец, А.Н. Логиновский // Труды ХХ Международной научно-технической конференции «Информационные средства и технологии» — Москва, 20–22 ноября 2012. — М.: МЭИ, 2012. Т. 1 – С. 72–80.

Рисунки к докладу

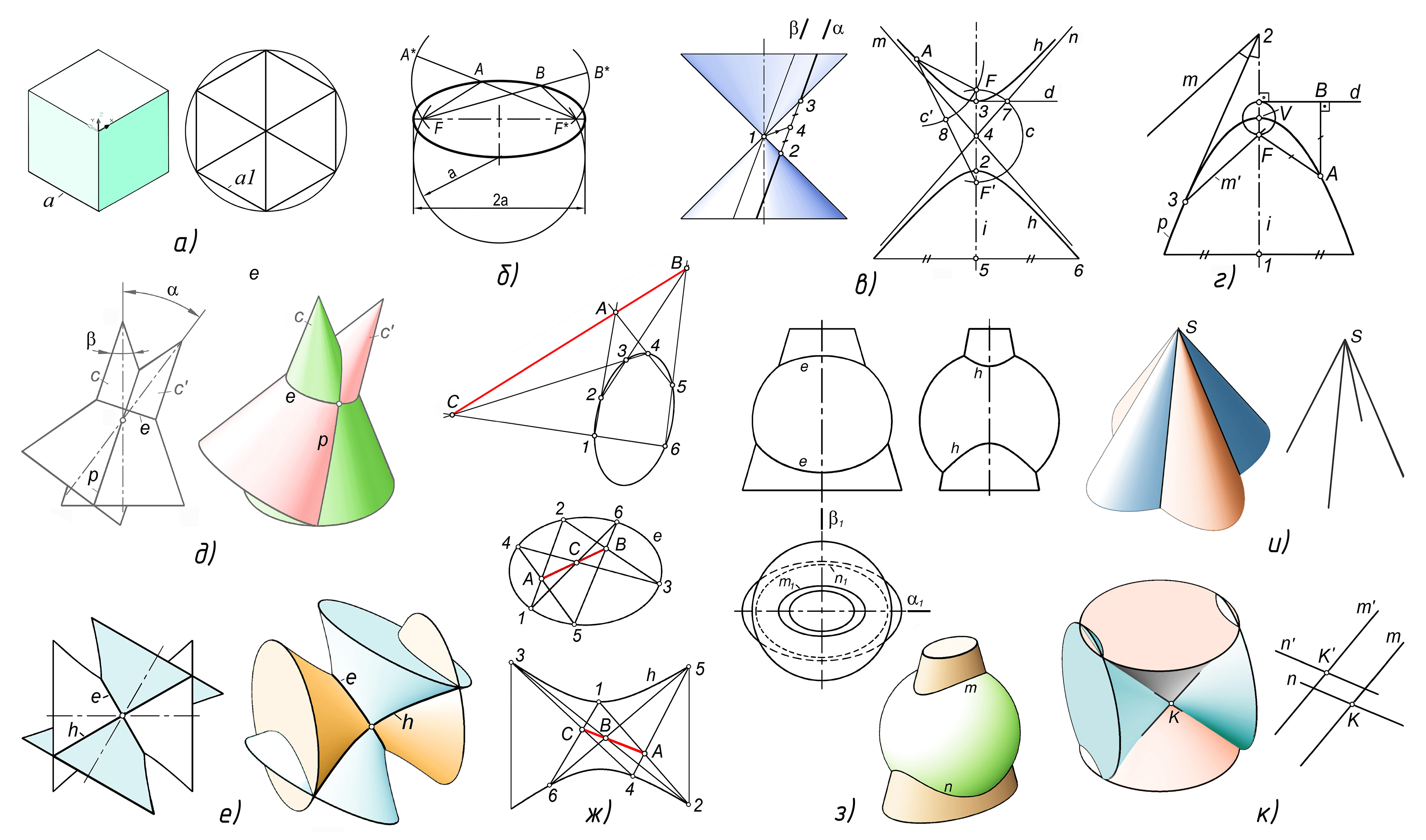
Тестирование погрешности компьютерных построений:

а – изометрия куба, б – “штатный” эллипс; в, г –  коники "штатной" квадрики; д, е – коники в пересечении штатных и нештатных квадрик; ж – тестирование по шестиугольнику Паскаля; з – точность построения проекций линий пересечения; и, к – точность построения прямых при пересечении квадрик.

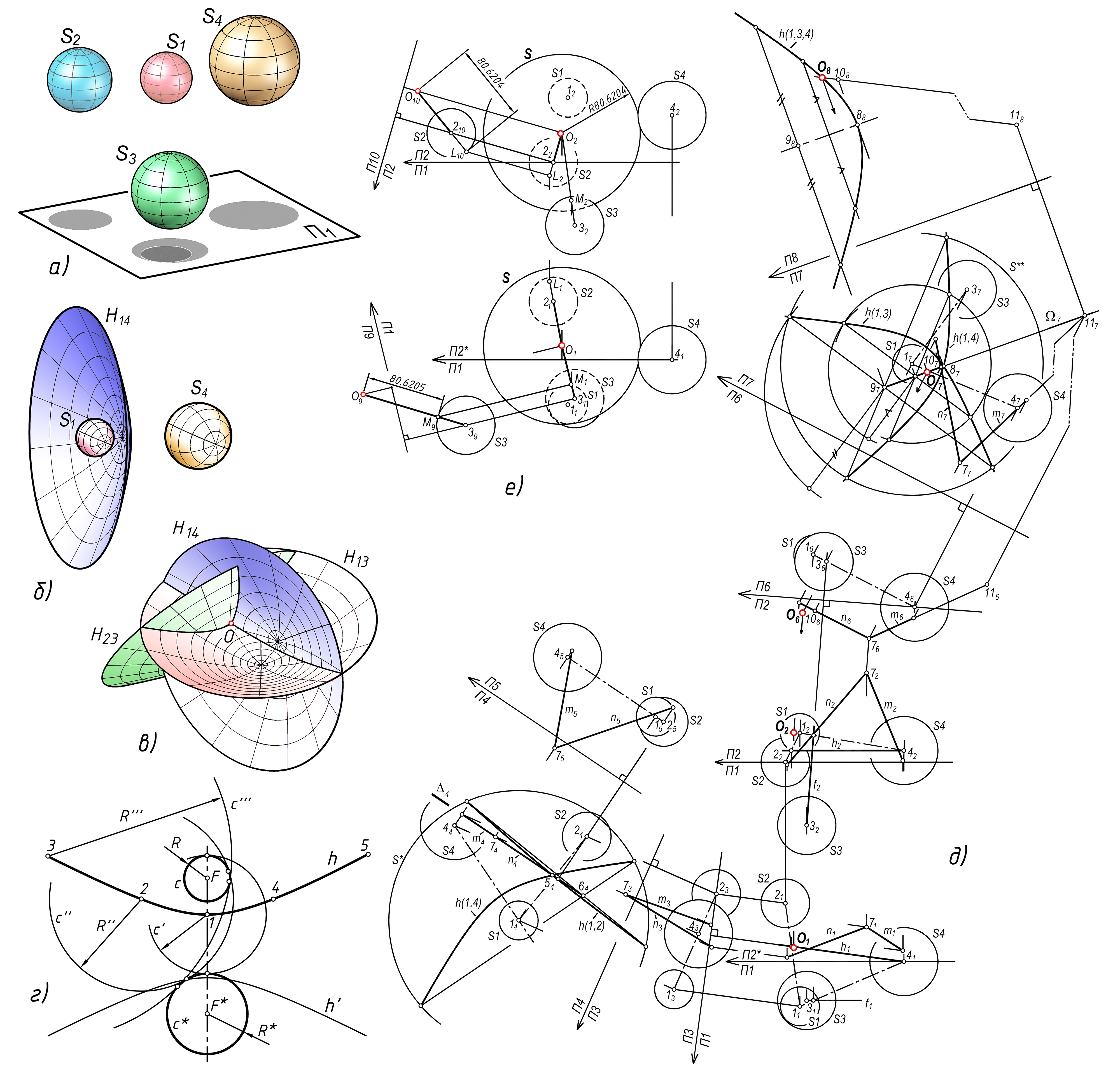
Задача Ферма:

а – заданные сферы; б – гиперболоид как ГМТ, равноудаленных от двух сфер; в – центр искомой сферы; г – построение гипербол; д, е – алгоритм НГ задачи Ферма.

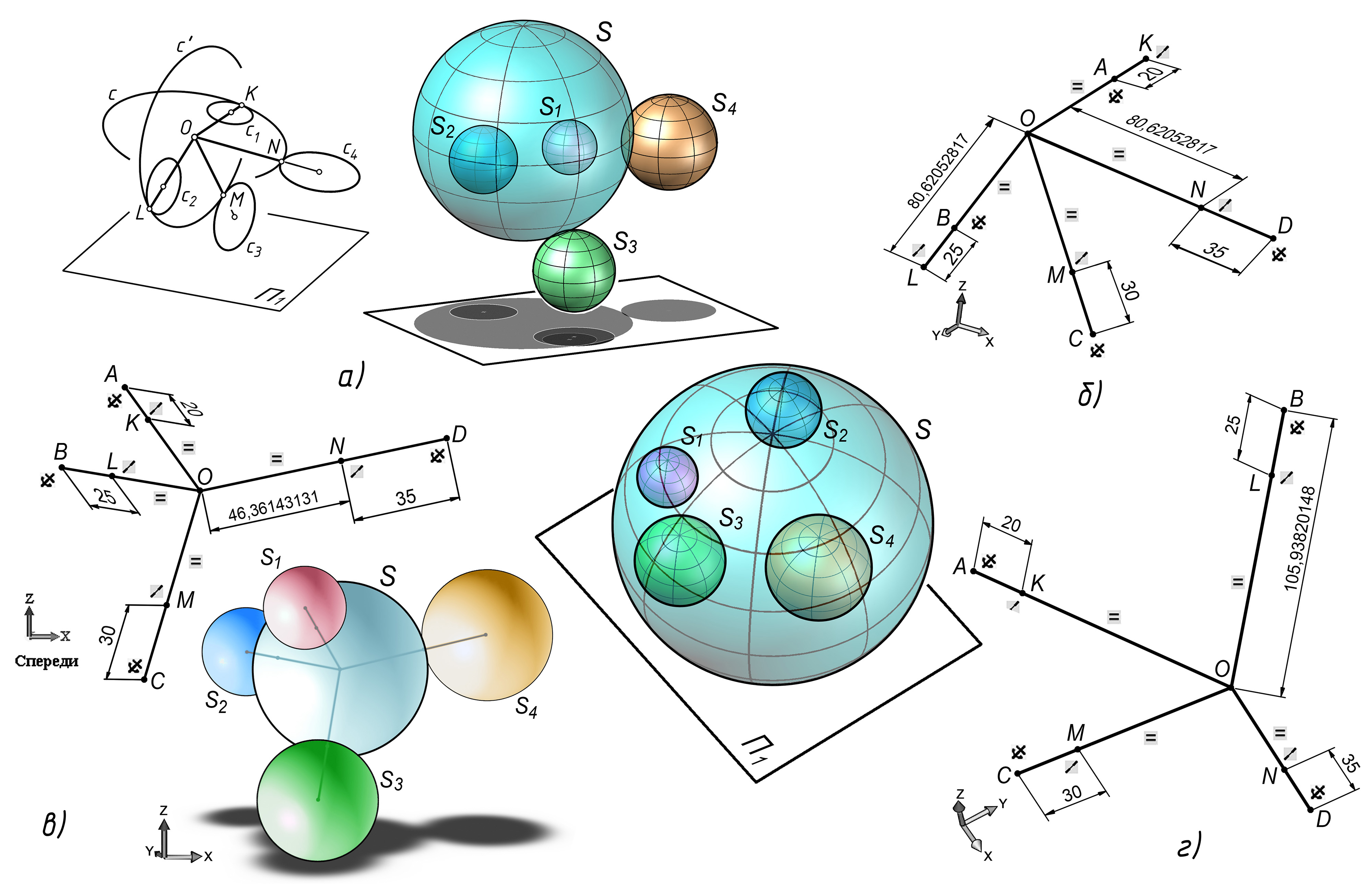
Задача Ферма (продолжение):

а – алгоритм 3D; б – алгоритм 3D параметризации при смешанном касании сфер; в – параметризация при внешнем касании искомой и заданных сфер; г – при внутреннем касании.

Бойков Алексей Александрович (17 марта 2016 г. 12:59)	Уважаемый Александр Львович, спасибо за доклад! Приведен обзор интересных задач и экспериментов. Полученные Вами результаты, в принципе, ожидаемы и не вызывают сомнения. К сожалению, в постановке задачи, и, следовательно, в выводах мне хотелось бы внести необходимые уточнения. >> Недоверие к компьютерной геометрической точности сторонники НГ используют как аргумент против активного перехода к 3D методам в учебном процессе Во-первых, геометрическая точность, к которой аппелируют сторонники конструктивной геометрии, имеет ценность не в прикладном, а в теоретическом, т.е. сугубо научном отношении. Например, практика вычислений показывает, что компьютерная реализация численного решения уравнения четвертого порядка работает быстрее, чем вычисления в радикалах (к сожалению, не могу привести источник, но идея состоит в том, что итерационные вычисления можно свести к быстрым арифметическим операциям). Отменяет ли это теоретическую ценность "точного" решения? Не стоит ли нам всю математику перевести на итерационные методы? Конструктивная геометрия циркуля и линейки имеет, в первую очередь, такую же теоретическую ценность, поскольку конкретная реализация алгоритма сведется к построению прямых и окружностей в AutoCAD'е или Компасе, геометрические ядра которых работают на численных методах. Не меньшую теоретическую ценность имеет геометрия сфер и плоскостей (впрочем, и любых других фигур - 3-, 4- и более высоких порядков) в трехмерном пространстве, 4-гиперсфер и 4-гиперплоскостей в четырехмерном и тп, если только мы будем решать задачи конструктивно и/или аналитически, а не перекладывать все на численные методы вычислений. Поэтому теоретическое решение средствами начертательной геометрии или трехмерного моделирования одинаково точны, а решения при помощи окружностей или сфер в Компасе - одинаково приближенны. Предположим, мы получили в решении n точек плоской фигуры, каждые 5 из которых при вычислении коэффициентов уравнения второго порядка дают одну и ту же конику. Можем ли мы утверждать, что нашли кривую второго порядка? Нет. Это останется лишь рабочей гипотезой, пока не будет найдено аналитическое или конструктивное доказательство, потому что может статься, мы нашли кривую, очень похожую на кривую второго порядка в пределах 8-10 знаков после запятой. Поэтому, >> Компьютерные 3D методы, особенно 3D параметризация, позволяют достаточно просто исследовать геометрические закономерности задач.  - на уровне гипотез, которые, в свою очередь, также требуют проверки и доказательства. >> Методы 3D лежат в основе современных САПР и активно развиваются. В отличие  от НГ, они являются актуальными и перспективными. Обучение им уже в первом семестре готовит студентов к освоению современных методов проектирования и геометрического моделирования Несомненно. В то же время начертательная геометрия показывает, что задачи, которые решаются на сферах и плоскостях (на гиперсферах и гиперплоскостях) могут быть сведены к окружностям и прямым, а это очень простые инструменты. Простые инструменты позволяют исследовать сложные геометрические формы. Не забывайте о неевклидовых геометриях, о комплексных координатах и т.д. - областях, без которых невозможно представить современную геометрию, и которые затруднительно моделировать в Компасе, AutoCAD, Inventor и др., но вполне возможно при помощи циркуля и линейки, если знать, как. Поэтому, (мой вывод) выпускающие кафедры, очевидно, должны достаточно времени уделять изучению современных инструментов прикладного геометрического моделирования. Фундаментальное геометрическое образование здесь не при чем. Это, конечно, идеальная ситуация. В реальности нас могут обязать учить трехмерным пакетам вместо геометрии, но уж стремиться к этому самим, я считаю, мы никак не должны. >> На студентов оказывает влияние и фактор эмоционального восприятия сопоставляемых алгоритмов. Вместо набора множества линий, карандаша и бумаги, которые до сих пор в учебном процессе остаются основными инструментами НГ,  решение 3D – это  современные компьютерные технологии, цвет, фотореалистичность. И, как следствие, неумение теоретизировать и проверять, если только в компьютерной программе нельзя рассмотреть предмет со всех сторон или выполнить измерения при помощи стандартного инструмента, т.е. мы будем учить студентов считать доказательством первичную оценку правильности гипотезы. >> Точность геометрических построений необходимо определять не по абстрактным критериям применения циркуля и линейки, а по реальной погрешности построений, которую можно измерить и сравнить с требуемым значением. В действительности, результат сравнения показывает, что геометрический редактор AutoCAD и вычислительная машина, считающая, к примеру, "a1 = a sin(arctg (sqrt 2))" находят один и тот же результат. Это просто здорово. (Мой вывод - )  В прикладных задачах, мы можем доверять как AutoCAD'у, так и вычислительной машине. При чем здесь точность геометрического решения и геометрия, в целом? с уважением, Бойков.
Гирш Антон Георгиевич (17 марта 2016 г. 16:09)	Здравствуйте, Александр Львович. Вы осветили конструктивную геометрию в непривычном ракурсе с позиций точности построений и сделали хороший вывод "Независимо от метода решения: НГ или 3D – залогом успешного решения является  понимание геометрической сущности задачи." Комментарий Алексей Александровича впечатляет своей спокойной аргументированностью "При чем здесь точность геометрического решения и геометрия в целом?". Можно только приветствовать: Ай да Бойков, ай да молодец!
Головнин Алексей Алексеевич (17 марта 2016 г. 21:59)	Здравствуйте Александр Львович! Я очень рад был увидеть Вас на конференции. Ваши доклады и выступления всегда дают и новые полезные знания и стимулируют к более глубокому осмыслению содержащихся в компьютерной графике возможностей. Сравнение Вами разных методов по критерию геометрической точности (ГТ), в конечном счете – еще одна убедительная демонстрация преимуществ компьютерных 3D методов перед методами НГ, пусть даже осуществлёнными на компьютере. Замечания и вопросы: 1. Насколько следует из статьи, Вы оцениваете точность абсолютной погрешностью (куб со стороной 100), а правильнее, наверное, - относительной. Ее величина в Ваших примерах будет на два порядка выше, впрочем, как и при других методах, но тем не менее. 2. Неожиданным, но от этого еще более убедительным выглядит Ваш вывод о значительно более высокой точности (на четыре порядка) при 3D-параметризации по сравнению с решениями по алгоритмам НГ и 3D. Тем более что этот результат проанализирован Вами. Не могу согласиться со спокойной реакцией по этому поводу Ваших оппонентов, так как даже в диссертациях 20-30% улучшения свойств уже обычно бывает достаточным. Но хочется также поделиться и сомнением: по методу параметризации использовалась программа SolidWorks, а по двум другим – AutoCAD. Но это навряд ли могло повлиять на результат. Очень изящным выглядит решение методом 3D-параметризации, где задача сводится к построению стержневой конструкции с заданным положением и размерами стержней. Геометрический смысл в чистом виде. Дальнейшие построения циркулем становятся просто неинтересными. Кстати по этому поводу вспомнилось воспоминание о Монже его учеников, что он при решении задач некоторое время сосредоточенно водил в воздухе руками, а потом, отработав таким образом ход решения, сообщал его своим ученикам и они получали ответ (это не дословно). В компьютерную эру эту утомительную по Монжу работу можно поручить компьютеру. Понимание же геометрической сущности задачи, о чем справедливо переживают Ваши оппоненты, остается за человеком. Кстати, высвободившееся в этом случае от собственно геометрических построений время можно направить на усиленные упражнения со студентами в области геометрического смысла в технических задачах. С уважением Головнин А.А.
Хейфец Александр Львович (17 марта 2016 г. 22:33)	Антон Георгиевич, здравствуйте, еще раз примите признательность за перекаченные мне Ваши книги. О земечении по моему докладу. Ваше первое замечание - положительное, спасибо. А со вторым не согласен. Конечно, это относится к Алексею Александровичу, его автору, но Вы его процитировали. Что же в нем хорошего, в этом замечании. Как можно рассматриваить геометрическое решение в отрыве от точности получаемого результата. Это и есть решение, "полученное языком" (см. мою статью), а не конструктивно-прикладное. А Алексею Александровичу я готовлю большой-большой ответ.  С уважением. А.Л. Хейфец
Хейфец Александр Львович (17 марта 2016 г. 22:41)	Алексей Алексеевич, спасибо за положительную оценку моей статьи. О абсолютной и относительной погрешности. Графические пакеты считают до 8-го знака после запятой, независимо от абсолютно величины параметра. То есть, здание в 10000 мм и модель в 100 мм, будут посчитаны до одной абсолютной величины 0.0000001 мм. Здесь, конечно, есть над чем задуматься, но по-моему, это так. С уважением. А.Л. Хейфец
Хейфец Александр Львович (17 марта 2016 г. 23:15)	Алексей Алексеевич, заблудился и не туда отправил ответ на Ваш вопрос об AutoLisp'e. Но Вы его увидите у Алексея Александровича. Он (тоже, извините за нескоромность) специалист в этом деле, и возможно, дополнит мой ответ. С уважением. А.Л. Хейфец
Хейфец Александр Львович (21 марта 2016 г. 9:45)	За целенаправленую бестактность    или .   С уважением. А.Л. Хейфец
Хейфец Александр Львович (21 марта 2016 г. 10:53)	Денис Вячеславович, здравствуйте. Выскажу мнение о Вашем комментарии (20.03.2016 15:49:12) к теме геометрической точности и многомерной геометрии. Вы считаете неправильным говорить о точности геометрии, применяя инструментальные средства: линейка, циркуль, компьютер.  Согласен, что термин “точность геометрии” – не понятен и сомнителен. Но речь не о нем, а о весьма конкретном термине и понятии  - реальной точности решения геометрической задачи. То есть о точности, которую можно измерить, сравнить с требуемым контрольным значением, предъявить заказчику. А не приводить ему: решил точно, поскольку довел до циркуля и линейки. О том, что компьютеру нельзя доверять, поскольку неясно как он работает.  Мало ли что мы не понимаем. Тестируй, проверь и применяй. Рассуждения о том, что компьютер строит  окружность как кривую Безье в контексте темы разговора.  Какая мне разница, как он ее строит. Я проверил, что в итоге погрешность  окружности равна восьмому знаку после запятой, этого с запасом, достаточно, чтобы ему доверять. Ваша фраза  в связи с ценой точности построений: “В глобальных масштабах мы имеем дело не только растранжириванием ресурсов, но и с невозможностью развития теории вследствие нарушения логики”. Вы о том, что деревянной линейкой дешевле и проще, а компьютер денег стоит? О второй части фразы – о нарушении логики и ошибках вычислений на компьютере –конечно, не следует слепо доверять компу. Но это разве аргумент против его применения. “Количество знаков после запятой – дело вторичное” – это количество является решающим фактором оценки точности и результата работы. А “адекватность и непротиворечивость модели” – так это само собой разумеющееся одно из условий достижения реальной точности решения. Ваши рассуждениях по nD,  о том, что прямую нельзя рассматривать как множество точек и др. комментировать не берусь. Пусть об этом думают те, кто видит в этом необходимость и понимает. О Вашей реплике, что в “моей” задаче Ферма “присутствует объект шестнадцати мерного пространства 16D”. Да, 16 параметров и 16 вариантов  решений, но изучаю я их через наше родное 3d – пространство. И о Симплексе. Вы постоянно пишете, как легко и элементарно все решили на своей замечательной разработке. Но в данном случае Вы решили только 2d – Аполлония.  Решите 3d со сферами, и сравните с моим результатом, приведенным в статье, тогда поговорим. С уважением. А.Л. Хейфец
Хейфец Александр Львович (22 марта 2016 г. 14:53)	Сергей Игоревич, Я полностью согласен с Алексеем Алексеевичем и, прежде всего, с его вопросом о том, как публикации по многомерностям и мнимостям  увязаны  с задачами  прикладных исследований секции КГП и, от себя добавлю, тематикой Советов по 05.01.01. К чему можно приложить эти исследования. Кроме геометрической эстетики (это мой термин) – никуда.  Тем более к учебному процессу. Но как я понял, Советы по 05.01.01 учебный процесс не интересует. В отношении себя добавлю, что в работе, которую я докладывал в Советах, в дополнении к теории инженерных подходов к 3d и их применению в учебном процессе, есть следующие прикладные разработки и внедрения: 1. Система расчета продолжительности инсоляции; 2. Система расчета области допустимой застройки, в основе которой лежит задача оптимизации. Я специально опубликовал эти работы ПНЖ 2012 №3 и 2013 №1, где Вы редактор секции, чтобы Вы обратили на них внимание. Не обратили. А по ним есть патент, авторские свидетельства на программы реализации и ряд действительных актов внедрения в архитектурных фирмах. Продолжу: 3. Автоматизированный коллоквиум для проверки правильности графических решений (сертификат на программу, внедрение в учебный процесс). Тот, который обсуждался здесь в докладе А.А. Бойкова. 4. Программа построения 3d геометрически – точной модели червячной фрезы, защищенная авторским свидетельством и актом внедрения в проектном институте в качестве компьютерного шаблона для контроля точности изготовления. Конечно, причина моих неудач в моей работе, да и не сумел донести, но считаю, что главное – это мое открытое выступление за реорганизацию кафедр в направлении 3d. Если Вы на предыдущей конференции говорили, что занимались разработкой 3d САПР на основе НГ, то все ясно. Так что не “обиженный” я, а недовольный. Интересно, снимет этот мой  ответ Ирина Дмитриевна с наклеиванием ярлыков, как уже бывало, или пропустит. С уважением. А.Л. Хейфец
Ротков Сергей Игоревич (22 марта 2016 г. 16:43)	Александр Львович! Тематика советов определена паспортом специальности 05.01.01, а не нашими прихотями. Там нет педагогических моментов. Там есть только технические науки. Все остальные указанные вами пункты, пусть даже они вами разработаны и получены патенты, только подтверждают наше мнение, что в вашей диссертационной работе нет внутреннего единства и логики, что требует Положение ВАК о диссертациях (см. соответствующий документ). Об этом вам говорилось во всех диссертационных советах. Я в совем личном ответном послании к вам определил, на что похожа ваша работа. Пока это не будет переосмыслено и переработано, говорить о возможном представлении работы в совет - бессмысленно. С уважением, С.И.Ротков.