ЭЛЕМЕНТЫ ТРИЗ В ЛЕКЦИЯХ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Описывается опыт использования элементов ТРИЗ при чтении лекций по начертательной геометрии студентам, обучаемым по направлению ракетная техника и космонавтика. Сделана попытка оценить результаты на базе анонимного опроса.

Для стимулирования процесса восприятия лекционного материала  автор статьи  периодически обращался к различным изобретательским задачам и элементам ТРИЗ (теории решения изобретательских задач) [1,2,3].   Трудности в изучении  начертательной геометрии возникают, по нашему мнению, по причине недостаточного количества прикладных задач и аналогий из жизненной практики.

На первой лекции студентам говорится о том, что приёмы решения задач начертательной геометрии во многом сродни приёмам решения задач изобретательских, теорию решения которых разработал выдающийся учёный Генрих Саулович Альтшуллер [4]. Он открыл основные законы изобретательства, и даже при решении жизненных трудностей успешно использовал их на практике. Например, поиск и разрешение противоречий. В тяжёлые времена после необоснованных репрессий, когда нужно было работать, а на работу не брали (вот вам противоречие), он разрешил проблему став писателем фантастом, попутно развивая и совершенствуя ТРИЗ.

Мы постоянно отмечаем необходимость развития устойчивой рефлексии у обучаемых, культуры мышления, как результата целенаправленного воздействия на процесс выполнения субъектом мыслительных операций с целью получения наиболее эффективных решений проблемных ситуаций. ТРИЗ выбран нами как инструмент для достижения этих целей.

При изложении понятий о центральном и параллельном проецировании уместно вспомнить древних изобретателей и предложить студентам подумать над решением такой задачи как определение высоты пирамиды Хеопса. После проведения «мозгового штурма» сообщить, как подобные задачи решал Фалес из Малета в 6 веке до нашей эры, дождавшись равенства длины палки, воткнутой в землю и её тени [5].    

При рассмотрении примера построения симметричной точки и других геометрических объектов обсуждаем проблемы симметрии в изобретательских задачах.

Изобретательская задача №1. Спортивный катамаран представляет собой два поплавка, соединенные площадкой, на которой стоит спортсмен. Чем  больше расстояние между поплавками, тем устойчивее катамаран. Однако перевернувшийся катамаран – именно из-за высокой устойчивости – невозможно  без посторонней помощи возвратить в первоначальное   положение. Как быть?

Решение: либо поплавки должны сдвигаться друг к другу, либо что проще мачта должна перемещаться из нижнего (опрокинутого положения в верхнее с тем, чтобы в дальнейшем можно было плыть на обратной стороне площадки (обе стороны одинаковы)). Для этого мачта должна быть шарнирно соединена с брусом на передней кромке площадки  [1]. (Построение симметричной точки). 

Изобретательская задача №2. Необходимо чтобы судно с достаточно высокой мачтой проходило под мостами. Для решения этой проблемы  надо  сделать на судне подвижную наклонную мачту и опускать ее  при прохождении  под мостами. Из жесткой системы сделали гибкую. Чтобы мачту было легче сгибать поставить противовес (аналог симметричной точки).

Также можно провести аналогию с симметричной точкой, рассматривая,  как  устроен старый шлагбаум и колодезный журавль.  Как лучше нести тяжелый лом? Задача уже обратная – надо найти середину лома, а концы лома представляют собой симметричные точки на равном расстоянии, тогда суммарный момент на опору (руку) равен 0 и нести лом легче.

Важно дать почувствовать студенту, что мы окружены разнообразными изобретениями. Часто к изобретению приводит факт констатации и разрешения противоречий.  Вещество или предмет обладает какими-то свойствами, но при этом  у него есть свои недостатки. Необходимо сохранить полезные свойства и минимизировать недостатки. Обсуждаем в качестве примера карандаш. Графитовый грифель обладает  положительным свойством – он оставляет след на бумаге, но это положительное свойство не обеспечивает прочности грифеля - он легко ломается.  Что придумали – поместить графитовый стержень в деревянный корпус.  С точки зрения теории решения изобретательских задач мы ввели Х-элемент, который позволил сохранить  положительные свойства и устранить недостатки. Роль х-элемента в этом случае выполняет деревянный корпус. Эта  система, как и вся система, не созданная природой, не идеальна.  Технический прогресс приводит к тому что, ведется дальнейшее улучшение системы или происходит  полный отказ от старой системы и переход  к новому изделию, каким- то образом заменяющему выполнение предыдущих функций. Если вернуться к карандашам, то они постоянно совершенствовались. Круглый карандаш скатывается со стола, поэтому придумали делать его шестигранным. Затем, для удобства, в верхнюю часть карандаша поместили стирательную резинку. Появились цветные карандаши, в которых вместо графита в грифелях используется мел со специальным клеем (каолин) и красящим веществом. Люди продолжали искать материал для замены древесины. Так появились карандаши в пластмассовой оправе. Был  изобретён механический карандаш в металлическом корпусе. Все это можно отнести к развитию старой системы.

В качестве замены старой системы на новую с выполнением функций старой идентифицируем работу на компьютере с графическими пакетами.   

Обсуждаем умение вводить Х – элемент в жизненных ситуациях. Возникает, например, такая  проблемная ситуация: надо отвернуть заржавевшую гайку, а необходимый момент силы обычным ключом не обеспечить. «Нарастить» рычаг можно  разными способами. Обсуждаем.

Изобретательская задача №3. Один из самых травматичных видов спорта - прыжки в воду. Что сделать, чтобы минимизировать травмы. Добавить пузырьки воздуха в жидкость. Пузырьки воздуха играют роль Х-элемента.

Теперь к начертательной геометрии. Рассмотрим задачу о том, как отложить на прямой общего положения отрезок, истинная величина которого известна.  Для решения  этой задачи без преобразования чертежа необходимо ввести вспомогательную точку, которая играет у нас роль   х - элемента.

Как найти недостающую проекцию точки принадлежащей плоскости? Вводим прямую, принадлежащую плоскости,  которая  у нас играет роль X-элемента.  

Использование плоскости уровня  в жизни – это задача про то, как добиться выравнивания фундамента или пола. «Изобретаем» уровень.    

Изобретательская задача №4. Есть пластина с большим числом разных отверстий. И есть деталь-шаблон. Необходимо предложить способ контроля детали (наличие лишних  и отсутствие нужных отверстий).

Ответ:  Контроль пластинки с просверленными отверстиями  ведут, совмещая желтое изображение пластинки с синим изображением эталона. Если на экране появляется желтый цвет, значит, в контролируемой пластинке отсутствует отверстие. Появление синего  цвета означает, что на пластинке есть лишнее отверстие. Эту задачу студенты обычно решают без использования цветовых контрастов.

Изобретательская задача №5. Авторское свидетельство №350219. При горячей прокатке надо подавать жидкую  смазку в зону соприкосновения металла с валками. Существует множество систем подачи смазки: самотеком, с помощью разного рода «щеток» и «кистей», под напором  (т.е. струйками) и т.д. Все эти системы очень плохи: смазка поступает в нужные места неравномерно и в недостаточном количестве, большая часть смазки  разбрызгивается, загрязняет воздух: нужно иметь десять разных режимов смазки – известные способы не обеспечивают такую регулировку. Требуется устройство, которое обеспечивает  поступление в нужные зоны нужного количества смазки – без потерь и без существенного усложнения оборудования.

По ТРИЗу лучший элемент, это тот которого нет, но функции его выполняются. Слово «нет» элемента означает что, например, элемент был введен в рабочую область, а затем выведен. Например, смазка на бумаге для прокатного стана,  бумага, затем сгорает, а смазка подается в область равномерно. По стандарту 5.13 «щетки-кисти», как и другие вспомогательные устройства, допустимы только в том случае, если они, сделав свое дело, сразу исчезают.

Решение: «Способ подачи жидкой смазки в очаг деформации при горячей прокатке, отличающейся тем, что с целью исключения  загрязнения окружающей среды и сокращения расхода, жидкой  смазкой пропитывают носитель, который подают в очаг деформации с прокаливаемым металлом, а в качестве носителя используют материал, ликвидирующийся  при температуре реформации,  например, в результате сгорания или испарения, в частности бумажную ленту (а.с. 589046).   

Проводим аналогию с начертательной геометрией, и рассматриваем  задачу о нахождении точки пересечения прямой с плоскостью. Плоскость и прямая имеют плохое взаимодействие друг с другом, если они занимают общее положение («в лоб задачу» не решить). Вводим Х-элемент, который есть, но которого как бы и нет (заключаем прямую в проецирующую плоскость). Х-элемент – проецирующая плоскость, об этом свидетельствует вспомогательная надпись у одной из проекций прямой. Ее не видно, но она есть и свойством собирательности обладает.  Находим линию  пересечения проецирующей плоскости с заданной плоскостью и определяем общую точку заданной прямой и линии пересечения плоскостей.

 Построение линии пересечения двух плоскостей.

1 способ. Вводим Х-элемент (удобный для нас) – проецирующую плоскость и  путем  его взаимодействия с объектами в задаче, находим 2 прямые по которым  пересекается Х-элемент с заданными плоскостями  и  находим общую точку, которая является одной из искомых. Далее  вводим  еще один Х-элемент (еще одну проецирующую плоскость) для нахождения второй точки.

Изобретательская задача №6. Имеется установка для испытания длительного действия кислот  на поверхность образцов сплавов. Установка представляет собой герметично закрываемую металлическую камеру. На дно камеры устанавливают образцы (кубики). Камеру заполняют агрессивной жидкостью, создают необходимую температуру и давление. Агрессивная жидкость действует не только на кубики, но и на стенки камеры, вызывая их коррозию и быстрое разрушение. Приходится изготавливать  камеру из благородных металлов, что чрезвычайно дорого. Как быть? Административное противоречие: нужно снизить стоимость системы. Конфликтующая пара -  не камера – жидкость,  а жидкость – кубик, камера и кубик не конфликтуют.  Нужно перейти от идеи защиты стенок к идее  вообще обойтись  без них. Как реализовать переход к паре кубик- жидкость.

Идеальный конечный результат (ИКР) – кубик и вокруг него агрессивная  жидкость. Реально этого не может быть – жидкость прольется.

Варианты решения:

1. Жидкость заменена вязким  веществом типа пластилина
2. Жидкость удерживается самим кубиком (для чего он должен быть сделан полым). Предпочтителен последний вариант: он не связан с изменением свойств самой жидкости.

Какие-то интересные мысли у студентов по поводу решения этой изобретательской задачи появляются. Ценным в этой задаче является то обстоятельство, что она заставляет перевернуть свои мысли с ног на голову. Жидкость не снаружи, а внутри!

Обратимся к начертательной геометрии и посмотрим в свете этой задачи на способы преобразования чертежа. В одном случае мы оставляем фигуру на месте и меняем плоскости проекции (обстановку), а других случаях, оставляем  систему плоскостей проекций и меняем  положение  фигуры. Тоже как бы, «выворачиваем с ног на голову». Переходим от жесткой системы к «гибкой».

Также были  разобраны  несколько задач с использованием 40 основных приемов устранения технических  противоречий [1].

В начертательной геометрии можно использовать следующие:

Прием 1. Принцип дробления

А) Разделить объект на независимые части.

Б) Выполнить объект разборным.

В) Увеличить степень дробления объекта.

Задача из практики. Грузовое судно разделено на однотипные секции. При необходимости можно делать корабль длиннее или короче.

В адаптированном варианте применительно к начертательной геометрии:  

1. Задачу разбить на несколько задач, последовательно выполняя которые необходимо подойти к решению. Например, если в задаче требуется выполнение каких-то двух условий, выполнить сначала одно условие, а затем второе.

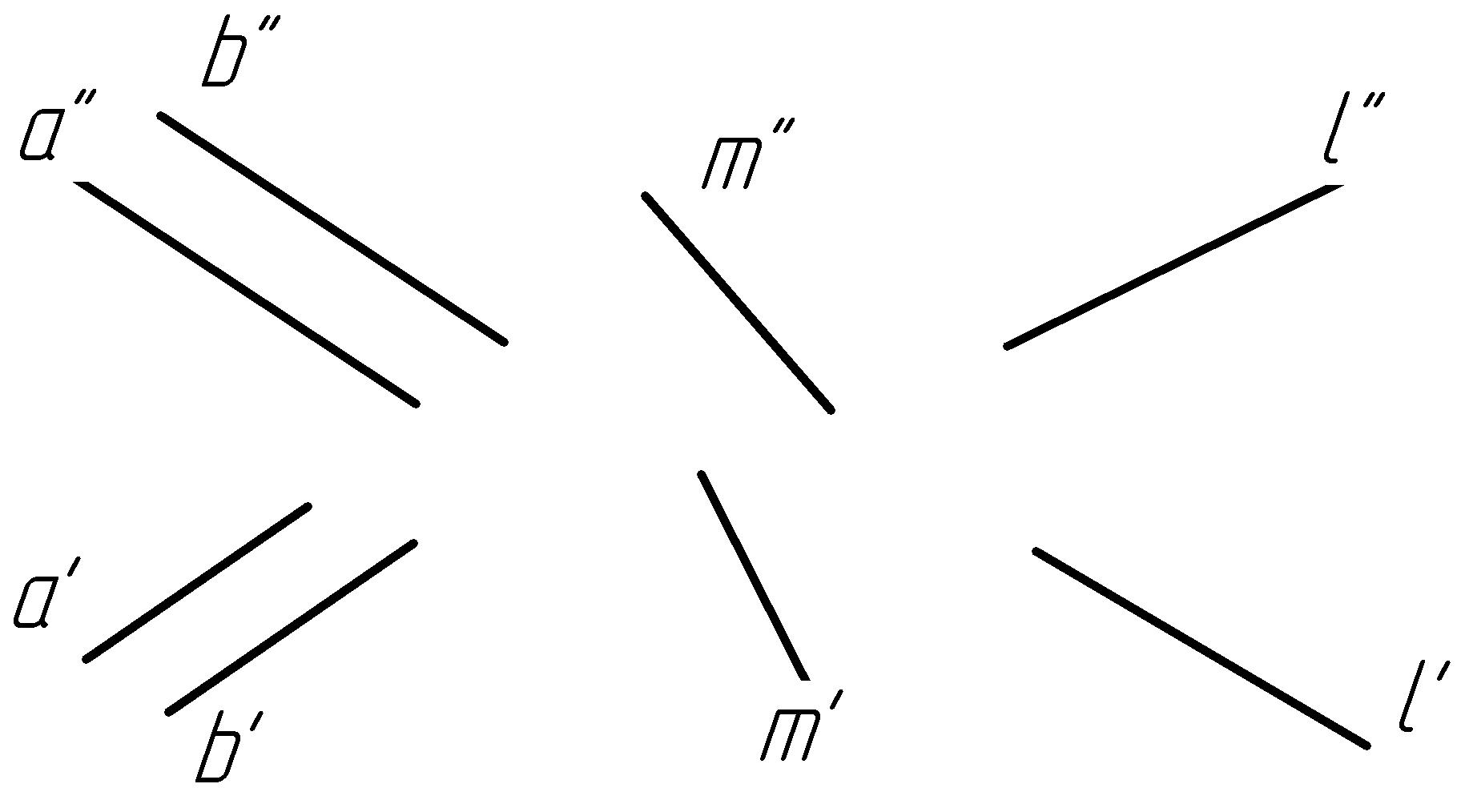
Задача. Провести  горизонталь,  пересекающую  прямые  l  и  m  и  параллельную  плоскости    ∑(a//b) (рис. 1).

Сначала  строим горизонталь в плоскости (а, b),  через точку на прямой m задаем прямую, параллельную горизонтали плоскости, и тем самым получаем новую плоскость. Затем пересекаем эту новую плоскость с прямой l , получаем  точку, например  1, и через нее проводим  прямую параллельную горизонтали плоскости. Пересекаем прямую m. Эта прямая будет искомая.

Прием 2. Принцип вынесения.

Отделить от объекта «мешающую часть» (мешающее свойство), или наоборот, выделить единственную нужную часть или нужное свойство.

 Пример.  Обычно на малых прогулочных катерах электроэнергия для освещения или других нужд вырабатывается  генератором, работающим от гребного двигателя. Для получения электроэнергии на стоянке приходится устанавливать вспомогательный электрогенератор с приводом от двигателя внутреннего сгорания. Двигатели естественно создают шум и вибрацию. Предложено разместить двигатель и генератор в отдельной капсуле, расположенной на некотором расстоянии от катера и соединенной с ним кабелем.   

В начертательной геометрии принцип вынесения можно использовать в задаче определения угла между двумя плоскостями, когда эта задача сведена к определению угла между двумя перпендикулярами. Построили перпендикуляры к плоскостям. Далее взяли произвольную точку на свободном поле  листа  и провели через нее  прямые параллельные этим перпендикулярам, а далее методом преобразования чертежа определяем истинную величину угла между пересекающимися прямыми. 

Прием 13. Принцип наоборот.

А) Вместо действия диктуемого условиями задачи, осуществить обратное действие.

Б) Сделать движущуюся часть объекта или внешней среды неподвижной, а неподвижную движущейся.

В) Перевернуть объект вверх ногами, вывернуть его.

 Построение антицентра.

Прямые a и b задают зеркало, луч из точки А падает на зеркало, отражается и попадает в точку В. Найти точку падения луча на зеркало. Строим из точки А перпендикуляр к плоскости зеркала, находим точку встречи перпендикуляра с плоскостью, а затем от точки встречи откладываем на перпендикуляре в сторону противоположную  расположению  точки А,  расстояние  равное расстоянию от точки А до точки встречи (антицентр). После чего соединяем полученную точку с точкой В и опять решаем задачу на точку пересечения прямой с плоскостью. Найденная точка будет искомой точкой, в которой луч будет отражаться от плоскости зеркала.

Прием 17. Принцип перехода в другое измерение.

Пространственную задачу сначала решить на плоскости, если это возможно.

Построение квадрата АВСD, со стороной ВС на прямой l. Или задача о  поиске множества точек равноудаленных от двух точек.

Поверхности.

Если рассмотрим пересечение линии с поверхностью, то для построения точек пересечения линии с поверхностью полезно преобразовывать  одну из проекций линии в проецирующую  цилиндрическую поверхность, считая, что данная проекция это след-носитель [3]. Эту цилиндрическую поверхность можно также считать Х-элементом, который помогает нам решить задачу.

Прием 10. Принцип предварительного действия.

А. Заранее выполнить требуемое действие (полностью или хотя бы частично).

Б. Заранее расставить объекты так, чтобы они могли вступить в действие без затрат времени на доставку и с наиболее удобного места.

 В начертательной геометрии:

Задать несколько образующих принадлежащих поверхности. Провести кривую, построить проекции этой кривой и на проекциях. И указать на ней точку.

При рассмотрении кривых второго порядка особое внимание было обращено на эллипс и параболу. Фокальное свойство эллипса (определение эллипса). Эллипс является геометрическим местом точек, для которых сумма расстояний от двух заданных точек (фокусов) есть величина постоянная (2а).

Изобретательская задача №7.  В сосуде  с жидкостью размещен источник ультразвука и биологический препарат. Ультразвук  распространяется  во все стороны, на биологический препарат попадает небольшая часть излучения, идущая по прямой линии «источник- препарат», да еще некоторая часть колебаний, случайно отраженных от стенок сосудов. Как повысить эффективность установки?

 Студенты предложили форму  эллипса  (эллипсоида вращения).

 Ответ на изобретательскую задачу (А.с. 988288):

Устройство состоит из сосуда 1, выполненного в форме эллипсоида вращения. В одном из фокусов  Г, которого установлен источник ультразвуковых колебаний 2, а во втором фокусе Г размещают биологический объект 3.  Источник ультразвуковых колебаний 2 может  быть, например,  сферическим  и возбуждать, соответственно, внутри сосуда колебания  со сферическим волновым фронтом. Ультразвуковой генератор, питающий источник 2, находится вне сосуда.  (Лучи, отражаясь от стенок сосуда, попадут в фокус.)

Эллипсоид вращения – это фигура вращения в трехмерном пространстве, образованная при вращении эллипса вокруг одной из его главных осей. Свойство вытянутого эллипсоида вращения отражать лучи, направленные в один из  фокусов, в другой фокус, используется в телескопах системы Грегори и в антеннах.

Основное свойство параболы: парабола является геометрическим местом точек, равноудаленных от данной точки (фокуса) и от данной прямой (директрисы). Параболоид вращения (поверхность второго порядка образован вращением параболы). Часто используемое свойство параболоида вращения  собирать пучок лучей, параллельной главной оси, в одну точку фокус, или наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основаны параболические антенны, телескопы- рефлекторы, прожекторы, автомобильные фары.       

Пересечение поверхностей.

Рассчитать поворот трамвая, машины (вынос) – поверхность вращения пересекается с поверхностью другого автомобиля. Поворот двери. 

 Развертки поверхностей.

Существует еще один прием ликвидации технического противоречия:

Прием 11. Принцип «заранее подложенной подушки».

Если рассматривать это «впрямую» как раз получается развертка поверхностей. Т.е. подкладываем плоскость, а затем совмещаем с ней поверхность.

Что касается ТРИЗ, там этот способ трактуется следующим образом. Компенсировать относительную невысокую надежность объекта заранее подготовленными аварийными средствами. Работает какая-то система, в процессе эксплуатации может случиться аварийная ситуация. Заранее предусматриваются средства, которые или ликвидируют повреждения или уменьшают ущерб. В годы Великой Отечественной войны в Ленинграде в августе-сентябре 1941 года начались страшные бомбежки. Руководство города организовало создание специальных групп, которые обработали все чердаки города  противопожарной смесью.  Это существенно сократило количество  пожаров [6]. Вот несколько подробностей, относящихся к этой истории: «На Невском химкомбинате остался невывезенный суперфосфат. Много — чуть ли не сорок тысяч тонн. Ценнейший, так называемый двойной суперфосфат, совершенно не содержащий балласта, каковым обычно является сульфат кальция. Стали думать, как переработать суперфосфат на вещества, обычно применяемые для пропитки дерева. К счастью, нашелся простой состав, который и антипиреном оказался отменным, и прилипал достаточно хорошо: на три части суперфосфата — одна часть воды. Обмазывать им надо трижды.

В первые послевоенные годы жильцы верхних этажей ленинградских домов часто жаловались на протекающие крыши: суперфосфат вызывал усиленную коррозию кровельного железа, оно проедалось ржавчиной с невиданной быстротой. Кровельщики, не понимая, в чем дело, терпеливо меняли лист за листом. Те же, кто был в курсе дела, об этих расходах не жалели...» [6].

Еще один пример. «Способ обработки неорганических материалов, например стекловолокон, путем воздействия плазменного луча, отличающийся тем, что с целью  повышения механической прочности  на неорганические материалы предварительно наносят  раствор или расплав  солей щелочных и щелочно-земельных металлов». Заранее наносят вещества, «залечивающие» микротрещины.

Для того, чтобы оценить промежуточные результаты, получить некую обратную связь, мы провели анонимное анкетирование, попросив студентов ответить на следующие вопросы:

1. Понравился Вам или нет предмет начертательная геометрия?

2. Что особенно понравилось или не понравилось в лекциях по начертательной геометрии?

3. Вызвало ли интерес использование некоторых аналогий с теорией решения изобретательских задач?

4. Какая тема для Вас оказалась труднее всего?

Главным результатом, полученным в результате анализа анкет, следует считать тот факт, что абсолютно все студенты положительно отнеслись к предмету. Несомненен интерес к ТРИЗу у большинства, а один студент написал, что стал изучать труды Г.С. Альтшуллера.

В заключение хочется процитировать Святителя Игнатия Брянчанинова, который в письме к Стефану Дмитриевичу Нечаеву  (17 января 1842 года) стр.352 [7] отмечал: «Мы ветрены: количество знаний, которое возрастает с возрастом мира, мы имеем  большее, нежели наши предки; это самое многознание делает нас поверхностными, и мы уступаем  предкам в качестве знаний, в сущности знания. А ветреность – от стремления  к пустым веселостям». Сейчас эта проблема возросла многократно. И задача каждого преподавателя сделать свой предмет не проходным. 

Заканчивая курс лекций, мы рассказываем студентам  притчу [8]:

Список литературы

1. «Конструктивные  задачи  в  проекционном  моделировании», Учебное пособие, Балт. Гос. техн. ун-т. «Военмех» Спб., 2001,62с. 3.85п.л./0.85п.л. Д.Е. Тихонов-Бугров, Ракитская М.В.
2. Ракитская М.В. «К проблеме развития рефлексии при обучении начертательной геометрии» Сборник трудов конференции: ФБГОУ «Пермский национальный исследовательский политехнический университет» V МЕЖДУНАРОДНАЯ ИНТЕРНЕТ-КОНФЕРЕНЦИЯ «Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации» КГП-2015, 0.5 п.л.
3. Как решить задачу. Методические указания по решению геометрических задач повышенной сложности. А.Г.Гирш. Омск-1986г
4. Альтшуллер Г. Найти идею: Введение в ТРИЗ – теорию решения изобретательских задач/ Генрих Альтшуллер. – 8-е изд. – М.: Альпина Паблишер, 2015.-402 с.
5. Теории решения изобретательских задач/ Меерович М.И., Л.И. Шрагина. –Минск: Харвест, 2003. -428,[4] c/ - (Библиотека практической психологии).
6. А.Н.Ардашев. Зажигательное и огнемётное оружие. М.: Яуза: Эксмо, 2009
7. Полное собрание писем : В 3 т.Т.3: Переписка с мирянами/ Сост. О.И.Шафранова. –М.: Паломник, 2011. -672с.
8.  Жил человек… Сборник христианских притч и сказаний/ Сост. О.Клюкина –М.: Никея, 2011.-192 с.:ил.

Рисунки к докладу

Горнов Александр Олегович (19 февраля 2016 г. 18:35)	Мария Валентиновна, здравствуйте! Не просто с удовольствием, а с большим удовольствием читаю и второй  Ваш доклад  на полях КГП. Может быть, Вы заметили в моем “кулуарном тексте” мысль о необходимости поиска форм организации и содержания учебного процесса, увлекающих учащихся. Уверен, Вам  это удается! Наверняка в нашей аудитории  много коллег, которые поддерживают такие подходы и один, среди них,  я. Успехов, А.О.
Лепаров Михаил Николаевич (19 февраля 2016 г. 22:30)	Здравствуйте, уважаемая Мария Валентиновна! Рад здороваться с Вами на этой конференции. Вы сдержали обещание с прежней конференции. По моему у Вас замечательное постижение. Поздравления. Я сам из отряда Александра Олеговича и  восхищаюсь творческих постижений. У меня следующие вопросы: 1.  Не трудно  поставить  задача студентам, чье решение ты знаеш. Ты подсказываешь путь (при необходимости) и перестаешь поиска когда решение получено. Ваш подход вызывающий и занимательный для студента, но он  будет плодоносный если какой- то студент успел предложит подход  решения задач НГ, которой неизвестен ему, а  дай бог – неизвестен Вам. Что то подобного у Вас было (кроме оптических свойств эллипсоида вращения) ? 2. Как  подбирали принципы Альтшулера- по успеху нахождения подходящую аналогии в НГ? Если так, рекомендую включить и 1-2  „неподходящие” и посмотреть активно что получеться. 3. О лекции понятно, что- то подобное в упражнениях было? 4. Успех Ваши студенты- изобрататели можно сравнить каким то образом обективно с другим студентами? Серезный шаг сделан. Рекомендую горячо следующий шаг. Еще раз поздравления Пожалуйста, извините мой русский. МЛ
Ракитская Мария Валентиновна (19 февраля 2016 г. 23:09)	Здравствуйте, Александр Олегович! Спасибо за поддержку! Часто очень сложно ломать старое, привычное и вводить что-то новое. Порой в погоне за новым выбрасывается что- то хорошее из старого. Все время все менять - то же, как "скользить по поверхности". Нужна золотая середина.М.Р.
Ракитская Мария Валентиновна (19 февраля 2016 г. 23:24)	Уважаемый Михаил Николаевич, Я тоже очень рада встрече с Вами и Александром Олеговичем. Спасибо за доброе отношение к моим экспериментам. Ваши языковые погрешности с лихвой компенсируются Вашими отличными замечаниями и идеями. Отвечаю по порядку: 1. Да такое было и не раз при подготовке ребят к олимпиаде В.И.Вышнепольского (см. его статью), когда работала с победителем Ваней Еньшиным. 2. Подбирала подходящую аналогию. Ваша идея замечательная. Спасибо. Обязательно попробую. 3. Начинаю пробовать на практике в своих группах и прощуповую нужный подход (пока не до конца мне ясно как). 4. По практическим занятиям, те группы, что прошли через мои лекции, справились с программой успешнее. Может просто состав оказался лучше? Хочется думать, что это не так.  Ещё раз спасибо. М.Р.
Зеленовская Наталия Вячеславовна (20 февраля 2016 г. 14:47)	Здравствуйте, Мария Валентиновна. Спасибо за красивую подачу материала. Опыт аналогичный, наверное, применяется всеми, но фрагментарно. У Вас под это интуитивное дело подведена красивая теория. Это здорово.  Часто студенты моего вуза, готовясь к конференциям, тоже находят интересные факты,  и привязывают их к конкретному изучаемому материалу. Аудитория всегда хорошо принимает такую информацию. А я, спросясь разрешения, вставляю "куски" доклада в лекционный курс. К примеру вот такая информация "Если сделать зеркало в форме эллипса и поместить в один из фокусов источник света, то лучи, отразившись от зеркала, соберутся в другом фокусе. Так же распространяются и акустические волны, что используют архитекторы для создания поразительных звуковых эффектов: «говорящих» бюстов, «магического» шёпота, «потусторонних» звуков. Это свойство лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружений, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико." Этот текст сопровождается рисунком, может сопровождаться анимацией. И лекцию я могу назвать, к примеру "Занимательные свойства кривых 2-го порядка". Даже такое название уже "подогревает" интерес студентов к материалу.   Спасибо за доклад.
Шацилло Людмила Анатольевна (20 февраля 2016 г. 21:35)	Мария Валентиновна, дорогая моя! Дождитесь моих внуков в Ваш институт (сейчас в 5 классе и книжку "Построения циркулем" осваиваем). Как у Вас интересно! Где взять книжки п.1 и 3 из  Вашего списка литературы?  С искренним уважением, Л.А.
Шахова Алевтина Бруновна (20 февраля 2016 г. 22:41)	Уважаемая Мария Валентиновна, с интересом прочитала Ваш доклад,  присоединяюсь ко всем репликам произнесенным выше нашими коллегами, интересно очень красиво привязано, восхищаюсь.... Единственный вопрос где берете время во время занятий,  или это для избранных факультатив, в рамках 9-8 лекций это очень не просто, у Вас очевидно их больше. Правда результативность выступления ваших студентов на олимпиадах доказывает школу ВОЕНМЕХа. С уважением Шахова А.Б.
Ракитская Мария Валентиновна (20 февраля 2016 г. 23:09)	Здравствуйте, Наталия Вячеславовна!  Спасибо за поддержку и за  развитие темы с эллипсом. Использую. С благодарностью. М.Р.
Ракитская Мария Валентиновна (20 февраля 2016 г. 23:14)	Дорогая Людмила Анатольевна. СПАСИБО! Осваивайте циркульное дело обязательно.   Многие студенты циркулем не владеют. Сначала карандаш и бумага. Компьютер потом. Настраивайтесь лет на 12, как минимум, будем учить внука вместе. По №1 буду искать электронную  версию. №3 вышлю. Думаю, Антон Георгиевич не будет против. Спасибо ему большое. С почтением к Вам, М.Р.
Ракитская Мария Валентиновна (21 февраля 2016 г. 15:25)	Здравствуйте, Алевтина Бруновна! Спасибо, что   откликнулись на мой доклад. Времени у нас действительно много: 2 часа лекций и 2 часа практический занятий по начертательной геометрии в неделю для большинства факультетов, плюс время  самостоятельной работы студентов под руководством преподавателя   2 раза в неделю по 2 часа, плюс индивидуальные занятия со студентами при подготовке к олимпиаде. С уважением М.Р.
Дударь Елена Сергеевна (24 февраля 2016 г. 10:15)	Добрый день, Мария Валентиновна! Рада видеть Вас на очередной конференции. Спасибо за увлекательную публикацию, в которой видится как профессионализм, так и энтузиазм педагога. Мне всегда были интересны задачи о «геометрических местах точек», в них в полной мере проявляются и логика, и абстрактное мышление. Пытались  ли Вы выполнить классификацию по принципу, какие приемы (принципы) ТРИЗ наиболее эффективны для решения определенного класса задач?  Может быть, есть закономерность... С пожеланиями удачи, Елена Дударь.
Ракитская Мария Валентиновна (24 февраля 2016 г. 17:59)	Здравствуйте, Елена Сергеевна! Благодарю, что откликнулись.   Согласна с Вашим утверждением о значении задач о геометрических местах. В нашей рабочей тетради по НГ есть ряд задач на эту тему.Пожалуй лучших.  Что касается классификации - интересная идея, но мне до этого пока далеко. Идёт мучительный поиск задач, применимых при обучении НГ и ИГ. С уважением и ответным пожеланием удачи, М.Р.
Бойков Алексей Александрович (26 февраля 2016 г. 16:00)	Здравствуйте, Мария Валентиновна!  Спасибо за интересный доклад, я сам нокоторое время присматривался к ТРИЗ, читал работы Альтшуллера и его учеников и даже подумывал включать те или иные элементы в учебный процесс, но все-таки пришел к выводу, что ТРИЗ слабо формализуема (что конкретно в той или иной задаче считать Х-элементом? почему в одной задаче это точка, в другой - прямая, в третьей плоскость?). В частности, глядя на примеры в докладе у меня создалось впечатление, что методы ТРИЗ и решения некоторых предложенных задач, что называется, "притянуты" (например, "подушка" - плоскость развертки?). Многие предложенные задачи легко решаются через применение формальных геометрических процедур, в частности, с опорой на понятие "геометрического места", - метод, хорошо зарекомендовавший себя в геометрии. Причем, дают гарантированный результат. С другой стороны ТРИЗ - это целый комплекс методов, заслуживающий отдельного цикла лекций и практических занятий, и тут мы уже рискуем перетянуть одеяло с начертательной геометрии. А оно и так короткое. В общем, задумка интересная, и от себя хочу пожелать вам успехов, буду наблюдать с предельным вниманием. Если позволите, я также попробую ответить на вопрос, заданный вами в комментариях к докладу Антона Гергиевича. Для нахождения произвольного числа общих точек конуса и сферы можно воспользоваться следующими соотношениями: Во втором случае имеем аналитическую реализацию традиционного алгоритма НГ со вспомогательными секущими плоскостями. В обоих алгоритмах найденные координаты пар точек следует сохранять в разные массивы (разделяя на верхнюю-нижнюю или ближнюю-дальнюю). Ни тот, ни другой алгоритм, впрочем, не находят контурных точек (1 рода), для чего в общем случае пришлось бы пересекать пару коник (см. доклад Д.В. Волошинова), и не реализуют проверку видимости. Литература, которая может быть полезна студентам: Точки, прямые, плоскости, преобразования:  1. Ананов Г.Д. Графоаналитическая геометрия. Л.: ЛИСИ, 1975. 116 с. http://f.webtute.ru/indexcol.php?id=5&m= Программирование в преподавании НГ:  2. Михайленко В.Е. Применение ЭВМ в преподавании курса начертательной геометрии / В.Е. Михайленко, В.А. Анпилогова, Н.И. Седлецкая. Киев: КИСИ, 1979. 68 с. http://f.webtute.ru/indexcol.php?id=11&m= 3. Курс начертательной геометрии на базе ЭВМ / А.М. Тевлин, Г.С. Иванов, Л.Г. Нартова и др. М.: Высшая школа, 1983. 176с. с уважением, Бойков
Лепаров Михаил Николаевич (26 февраля 2016 г. 17:24)	Здравствуйте, уважаемый Алексей Александрович! Разрешите сказать свое мнение. ТРИЗ является методом решения творческих задач и как таковой он является неформализован. По моему, золотое зерно  его применение в НГ является та самая неформализованность, которая дает возможность студента сам найти метод решения конкретной задаче, метод, которой ему до сих пор незнаком. (Другая польза является обучение по приложением ТРИЗ- а.) Пожалуйста, извините мой русский. С уважением мл
Бойков Алексей Александрович (26 февраля 2016 г. 18:57)	Уважаемый, Михаил Николаевич, бесспорно, ТРИЗ хорош для поиска "озарения", необходимого в решении творческой задачи; но, касаясь НГ и ИГ, я не вижу, где методы ТРИЗ могли бы помочь в решении задачи без знания геометрии. Наши студенты зачастую просто не знают геометрии, они умудряются получать весьма оригинальные решения, но не способны проверить, правильные эти решения или нет. Скажем так, если я увижу, как студент, сознательно применяя методы ТРИЗ (увеличение, уменьшение, наоборот, дробление, соединение, разделение в пространстве и времени, Х-элемент и др.), решит задачу олимпиадного уровня (вот уж где простор для творчества), я сразу и полностью поменяю свое мнение. Пока же я опасаюсь увлечься изучением ТРИЗ на примере некоторых задач НГ, вместо изучения самой НГ. с уважением, Бойков
Ракитская Мария Валентиновна (27 февраля 2016 г. 10:45)	Здравствуйте, Алексей Александрович! Feci quid potui, faciant meloira potentes! Что касается задачи, то в том виде, который описали Вы она легко решается. Конечно я не полностью сформулировала задачу. На самом деле задача не статическая, а динамическая. Вершина конуса (точка вне сферы) перемещается по какой-то троектории. Ось конуса не вертикальна. Конус задается углом наклона к оси конуса. Ось конуса не проходит через центр сферы. Необходимо в какие-то моменты строить линию пересечения конуса со сферой.  С уважением, М.Р.
Бойков Алексей Александрович (27 февраля 2016 г. 12:49)	Уважаемая Мария Валентиновна, тогда ваш случай легко сводится к моему случаю 1. Один, максимум два поворота системы коодинат (аффинная матрица M). Очередная точка траектории - координаты Sx, Sy, Sz. Остается найти эллиптическое сечение в какой-то горизонтальной (фронтальной/профильной) плоскости (на основе положения центра и угла при вершине конуса) - величины Ex, Ey, Ez и a, b. Рассчитать точки кривой пересечения. Повернуть точки обратно (матрица M^-1). у уважением, Бойков
Ракитская Мария Валентиновна (27 февраля 2016 г. 17:34)	Уважаемый Алексей Александрович! Спасибо за  подсказки. Если ко мне еще этот студент подойдет, я ему так и посоветую сделать. С благодарностью, М.Р.
Бойков Алексей Александрович (27 февраля 2016 г. 17:47)	Комментарий удален, т.к. нарушает структуру страницы "Последнее",  где он дублируется. Ширина рисунка в коменнтариях не должна превышать 500 точек растра! Для обмена более обширной информацией можно воспользоваться разделом "В кулуарах". С уважением к участникам, Администрация
Гирш Антон Георгиевич (1 марта 2016 г. 22:02)	Здравствуйте, Мария Валентиновна. Есть просьба не по теме, а как живущей в Питере. Если откажетесь, обид не будет. Есть такой автор НГ и проективной геометрии - Вольберг О.А., книги изданы в 1947, - 49 г. Хорошие книги, уважение автору. Но сколько не пыталсся расшифровать эти О.А. - без успеха. Трудился он в Ленинграде, в Пединституте. Мои поиски по Гуглю дали для О. ничего, мои допущения Осип, для А. - Абрамович, в книге жителей Питера за 1912 г. значится некий Вольберг Абрам. С уважением. А.Г.
Славин Борис Матвеевич (2 марта 2016 г. 0:12)	Уважаемая Мария Валентиновна! С большим интересом прочитали аш доклад. Действительно, современных студентов необходимо как-то заинтересовать, предложить им что-то необычное, нестандартное. В противном случае, большинство заметно скучает и с прохладцей относится ко всей информации. При изучении Вашего доклада мы пришли к выводу, что Вы наверняка были одним из руководителей команды студентов, блестяще выступивших на Всероссийской олимпиаде, и поэтому у нас возникло несколько вопросов в порядке возможного обмена опытом. 1) Какие задачи Вы с ними решали при подготовке и какими учебными пособиями пользовались? Или все задачи у Вас оригинальные авторские? 2) Сколько времени длится подготовка команды? 3) Третий вопрос меркантильный. Руководство вуза как оплачивает Ваши труды или все строится, по выражению руководства нашего вуза, "в счет второй половины дня? (Красивая фраза, не правда ли?) Поделитесь пожалуйста информацией насколько это возможно. С уважением, Славин Б.М., Харах М.М.
Тихонов-Бугров Дмитрий Евгеньевич (2 марта 2016 г. 0:18)	Здравствуйте, уважаемый Антон Георгиевич. Вольберга звали Овсей Аронович. Он погиб в блокаду.   С уважением, Тихонов-Бугров
Ракитская Мария Валентиновна (2 марта 2016 г. 15:38)	Уважаемый Борис Матвеевич! 1. Военмех родоночальник городских олимпиад (1979). По этой причине у нас большой банк оригинальных задач. Часть из них опубликована в книге «Лызлов А.Н., Ракитская М.В., Тихонов-Бугров Д.Е.: Начертательная геометрия. Задачи и решения. Спб. Лань, 2011». Начинаем с разделов «Остановка» в Военмеховском пособии «Начертательная геометрия, Шаг за шагом» в 3 частях. Кроме того конечно Пеклич. Подготовкой по КГ занимается К.О.Глазунов 2. В октябре уже выделяются способные люди, к которым применяется особый подход. Я провожу индивидуальную работу за месяц до городской олимпиады. С участниками Всероссийской олимпиады работаем постоянно. 3. Я получаю доплаты как заместитель заведующего кафедрой. Кроме этого руководство вуза регулярно премирует за успехи в олимпиадах. С уважением, Ракитская М.В.
Вышнепольский Владимир Игоревич (9 марта 2016 г. 1:05)	Уважаемая Мария Валентиновна! Как хорошо, что Вы упомянули Вашу с коллегами книгу "Начертательная геометрия. Задачи и решения". Не знал о ее существованиии, постараюсь достать. Вы, конечно, правильно делаете публикуя олимпиадные задачи! Уважаемые Борис Матвеевич и Матвей Максимович! У В.А. Пеклича помимо учебника "Начертательная геометрия", есть сборник "Задачи московких городских и российских олимпиад по начертательной геометрии", там собраны олимпиадные задачи с 1975 по 2003 гг., приведены их решения. Правда, условия не удобны для того, чтобы  решать - маленькие! С уважением, Вышнепольский,
Тихонов-Бугров Дмитрий Евгеньевич (9 марта 2016 г. 11:26)	Уважаемый Владимир Игоревич, как здорово, что Вы вернулись на конференцию. Вашего мнения по многим вопросам ждём. Книга с автографами авторов уже приготовлена. Выслать по адресу вуза или по другому?  Ваши: Лызлов, Ракитская, Тихонов-Бугров.