Назад Go Back

АНАЛИТИЧЕСКАЯ МОДЕЛЬ ПОВЕРХНОСТЕЙ НА ОСНОВЕ КООРДИНАЦИИ ПРОСТРАНСТВА ВИНТОВЫМИ И ЭЛЛИПТИЧЕСКИМИ ЛИНИЯМИ

English version
Презентация
Фото Кокарева Яна Андреевна (Донской государственный технический университет )


Аннотация

В статье рассмотрен алгоритм синтеза поверхностей путем погружения произвольной линии в конгруэнцию на основе конструктивно-параметрического метода формообразования. Получены параметрические уравнения координации пространства винтовыми и эллиптическими линиями, на основании которых определены u-, v- и w-конгруэнции. Визуализированы поверхности полученных конгруэнций. Определены общая структура поверхностей.



Ключевые слова: конструктивно-параметрический метод, формообразование, конгруэнция линий, координация пространства, криволинейные координаты

Формообразование поверхностей является неотъемлемой частью проектирования. С развитием технологий, методов расчетов, появлением новых материалов, позволяющих реализовать всё более футуристические проекты, развиваются и методы формообразования поверхностей.

Методы формообразования исторически развивались в соответствии с доступными способами визуализации и расчета конструкций: синтетический [1-3], конструктивно-синтетический [4-6], кинематический [7-9], метод преобразований [10-11], метод криволинейного проецирования [12-14], параметрический [15], методы представления кусочно-аналитическими функциями [8, 16, 17].

Наличие аналитической модели при проектировании сложных криволинейных форм упрощает расчеты конструкции. Однако часто по аналитическому представлению практически невозможно представить будущую форму поверхности. Одним из методов формообразования, который позволяет включить в уравнения поверхностей конструктивные элементы с задаваемыми параметрами, является конструктивно-параметрический метод, разработанный Скиданом И.А. и его учениками [18-22].

Цель статьи – синтез параметрических уравнений и визуализация поверхностей u-, v- и w-конгруэнций конструктивно-параметрическим методом на основе конструктивной схемы координации пространства винтовыми и эллиптическими линиями.

Суть конструктивно-параметрического метода сводится к тому, что используется конструктивная модель будущей поверхности в качестве переходной от задуманной к аналитической. При этом пространство параметризируется в соответствии с этой моделью, то есть создается конструктивная схема координации пространства заданными линиями в качестве координатных. При этом, с одной стороны мы задаем пространство криволинейными координатами, а с другой – эти же координатные линии образуют три взаимосвязанных конгруэнции линий. Для образования поверхности используется погружение линии в одну из конгруэнций.

Алгоритм синтеза параметрических уравнений поверхности, полученной путем погружения линии в конгруэнцию, состоит из следующих пунктов:

  1. Создание конструктивной схемы координации пространства линиями.
  2. Составление параметрических уравнений конгруэнции-координации в виде:

x=f1(u,v,w), y=f2(u,v,w), z=f3(u,v,w).               (1)

          Уравнениями (1) также задаются три конгруэнции: u-, v- и w-линий.

  1. Выражение криволинейных координат через прямоугольные декартовы:

u=φ1(x,y,z), v=φ2(x,y,z), w=φ3(x,y,z).               (2)

  1. Задание параметрических уравнений погружаемой в конгруэнцию линии:

X=F1(t), Y=F2(t), Z=F3(t).                                (3)

  1. Подстановка уравнений (3) в уравнения (2) вместо соответственно x, y, z:

u=φ1(X(t),Y(t),Z(t)), v=φ2(X(t),Y(t),Z(t)), w=φ3(X(t),Y(t), Z(t)).                    (4)

  1. В зависимости от выбранной конгруэнции линий (u, v или w) в уравнения (1) подставляются два уравнения (4), за исключением того, название которого входит в выбранную конгруэнцию. Например, для синтеза уравнений поверхностей конгруэнции w-линий в уравнения (1) подставляются выражения для u и v из уравнений (4):

x=f1(u(t),v(t),w), y=f2(u(t),v(t),w), z=f3(u(t),v(t),w).               (5)

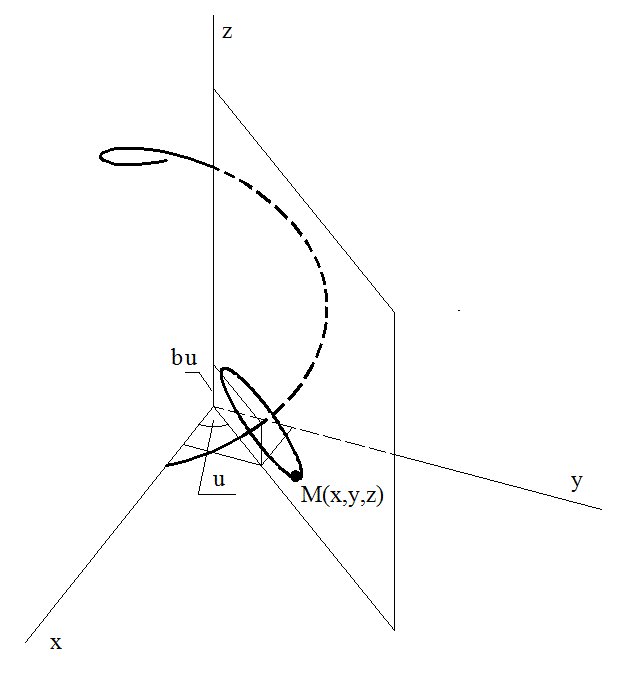
Рассмотрим конструктивную схему координации пространства винтовыми и эллиптическими линиями (см. рис. 1):

Фактически конструктивная схема представляет собой множество соосных винтовых поверхностей с подобными сечениями-эллипсами в плоскостях, перпендикулярных плоскости XOY.

Согласно выше приведенному алгоритму, составим параметрические уравнения конгруэнции-координации.

В плоскости сечения u=u0 уравнения плоского поля концентрических подобных эллипсов (s – коэффициент соотношения полуосей эллипса) с учетом параметра-радиуса a и параметра-шага b винтовой линии будут иметь вид:

x'=vcosw+a,y'=svsinw+bu.                  (6)

С учетом поворота плоскости найдем уравнения конгруэнции-координации:

x=x'cosu=( vcosw+a)cosu,

y=x'sinu=( vcosw+a)sinu,   (7)

z=y'= svsinw+bu.

Область определения функций (7) определяем, рассчитав якобиан и приравнянв его к нулю:

J=-vs(a+vcosw)=0.             (8)

Анализируя выражение (8), можно определить, что при v=0 мы получаем уравнение винтовой цилиндрической линии, на которой располагаются центры эллипсов, а выражение в скобках определяет плоское поле эллипсов.

Координатные поверхности заданной криволинейной системы координат:

Координатные линии:

Далее выполняя пункты 3-6 приведенного алгоритма, были получены изображения поверхностей u-, v- и w-конгруэнций, приведенные на рисунках 2, 3 и 4 соответственно. В конгруэнции (7) погружена астроида:

X=cos3t, Y=sin3t, Z=2.

Постоянные параметры конгруэнции: a=1.5, b=1, s=2. Сами уравнения выражений (2) и поверхностей (5) не приведены из-за громоздкости полученного результата.

Рассмотрим структуру полученных поверхностей.

  1. Поверхности u-конгруэнции являются винтовыми поверхностями, образующие которых пересекают погружаемую линию.
  2. Поверхности v-конгруэнции являются линейчатыми поверхностями с тремя направляющими: осью OZ, погружаемой линией и винтовой цилиндрической линией с параметрами a и b.
  3. Поверхности w-конгруэнции являются каналовыми поверхностями с эллиптическими сечениями, перпендикулярными плоскости XOY, центры которых образуют винтовую линию с параметрами a и b. Поверхность содержит погружаемую линию.

При приближении к значениям u=πn (n=0, 1, 2...) поверхности не определены.

Полученные типы поверхностей: винтовая, каналовая и линейчатая с тремя направляющими, - могут быть использованы в технических проектах и дизайнерских решениях.

Список литературы

  1. Reye T. Geometrie der Lage / T. Reye. – Leipzig, 1910. – T. 1-3.
  2. Salmon G. A Treatise on the Analytic Geometry of Three Dimensions / G. Salmon. – New York: Chelsa Publishing Company, 1965 (reprint). – 486 pp.
  3. Sanger R.G. Synthetic projective geometry / R.G. Sanger. – New York – London: McCraw – Hill Book Company, 1939. – 175 pp.
  4. Подгорный А.Л. Конструирование поверхностей оболочек по заданным условиям на основе выделения их из конгруэнций прямых [Текст] / А.Л. Подгорный // Прикладная геометрия и инженерная графика. – К.: «Будівельник». – 1969. – Вып. VIII. – С. 17-28.
  5. Підгорний О.Л. Створення комп’ютерних моделей нелінійчатої поверхні 3-го порядку методами синтетичної геометрії [Текст] / О.Л. Підгорний, В.М. Несвідомін // Прикл. геом та інж. граф. – К.: КНУБА. – 2008. – Вип.79. – С. 9-15.
  6. Михайленко В.Е. Формообразование оболочек в архитектуре [Текст] / В.Е. Михайленко, В.С. Обухова, А.Л. Подгорный. – К.: Будівельник, 1972. – 208 с.
  7. Короткий В.А. Компьютерное моделирование кинематических поверхностей [Текст] / В.А. Короткий, Е.А. Усманова, Л.И. Хмарова // Геометрия и графика. – 2016. – Т. 3. – №. 4. – C. 19-26. – DOI: 10.12737/17347.
  8. Голованов Н.Н. Геометрическое моделирование [Текст]: научное издание / Н.Н. Голованов. — М.: Изд-во физико-математической литературы, 2012. — 472 с.
  9. Кривошапко С.Н. Энциклопедия аналитических поверхностей [Текст] / С.Н. Кривошапко, В.Н. Иванов. – М.: Либроком, 2010. – 560 с.
  10. Иванов Г.С. Конструирование технических поверхностей (математическое моделирование на основе нелинейных преобразований) [Текст] / Г.С. Иванов. – М.: Машиностроение, 1987. – 192 с.
  11. Надолинный В.А. Основы теории проективных рациональных поверхностей [Текст]: дис. …докт. техн. наук: 05.01.01 / В.А. Надолинный. – М., 1989. – 202 с.
  12. Обухова В.С. Двуосевое проектирование кривых линий [Текст] / В.С. Обухова // Прикладная геометрия и инженерная графика. – К.: «Будівельник». – 1965. – Вып. I. – С. 39-47.
  13. Обухова В.С. Обобщение нелинейных систем проекций и одноосевые системы [Текст] / В.С. Обухова // Прикладная геометрия и инженерная графика. – К.: «Будівельник». – 1970. – Вып. 10. – С. 17-27.
  14. Сименко О.В. Проекціювання променями конгруенції циліндричних гвинтових ліній сталого кроку [Текст] / О.В. Сименко // Праці Таврійського державного агротехнічного університету. –  Мелітополь: ТДАТА. – 2004.  –  Вип. 4. – Т. 23.  – С. 86-91.
  15. Сальков Н.А. Параметрическая геометрия в геометрическом моделировании [Текст] / Н.А. Сальков // Геометрия и графика. – 2014. – №3. – С. 7-13. – DOI: 10.12737/6519.
  16. Замятин А.В. Алгоритм аппроксимации поверхности сплайнами [Текст] / А.В. Замятин, А.Е. Кубарев, Е.А. Замятина // Науковедение. 2012. № 3 (12). URL: naukovedenie.ru/sbornik12/12-90.pdf
  17. Barton M., Shi L., Kilian M., Wallner J., Pottmann H. Circular arc snakes and kinematic surface generation // Computer Graphics Forum “Eurographics”. –  2013.  – DOI:10.1111/cgf.12020.
  18. Сименко О.В. Аналітичні та комп’ютерно-графічні моделі нетрадиційних систем проекціювання та їхніх проекцію вальних поверхонь [Текст]: дис. … канд. техн. наук: 05.01.01 / О.В. Сименко. – Донецьк, 2006. – 216 с.
  19. Скідан І.А. Аналітичний опис еліптичної конгруенції прямих та її поверхонь [Текст] / І.А. Скідан, Я.А. Кокарєва // Праці Таврійського державного агротехнічного університету. – Мелітополь: ТДАТУ. – 2010. – Вип. 4. – Т.48. – С. 36-43.
  20. Кокарєва Я.А. Аналітичні та комп'ютерні моделі поверхонь конгруенцій першого порядку прямих [Текст]: дис. ... канд. техн. наук: 05.01.01 / Я.А. Кокарєва. – Макіївка, 2011. – 203 с.
  21. Кокарева Я.А. Параметрические уравнения конгруэнции прямых, заданной фокальными окружностями [Текст] / Я.А. Кокарева // Научное обозрение. –  2014. –  №11. –С. 689-692.
  22. Кокарева Я.А. Поверхности конгруэнции эквиаффинных образов окружности [Электронный ресурс] / Я.А. Кокарева // Инженерный вестник Дона. – 2016. –№4. – URL: http://www.ivdon.ru/ru/magazine/archive/n4y2016/3863.

Рисунки к докладу

Рис. 1
Рис. 1

Конструктивная схема координации пространства винтовыми и эллиптическими линиями




Рис. 2
Рис. 2

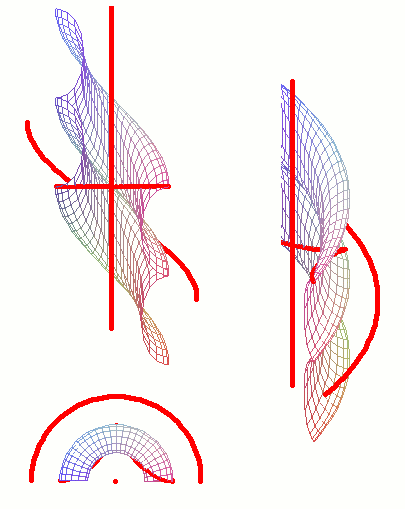
Пример поверхности u-конгруэнции




Рис. 3
Рис. 3

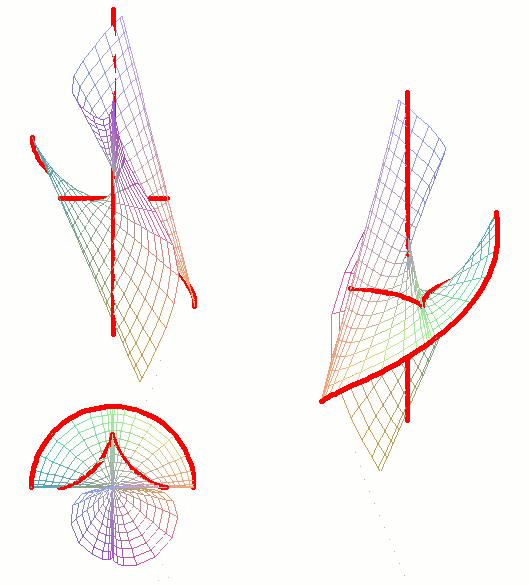
Пример поверхности v-конгруэнции




Рис. 4
Рис. 4

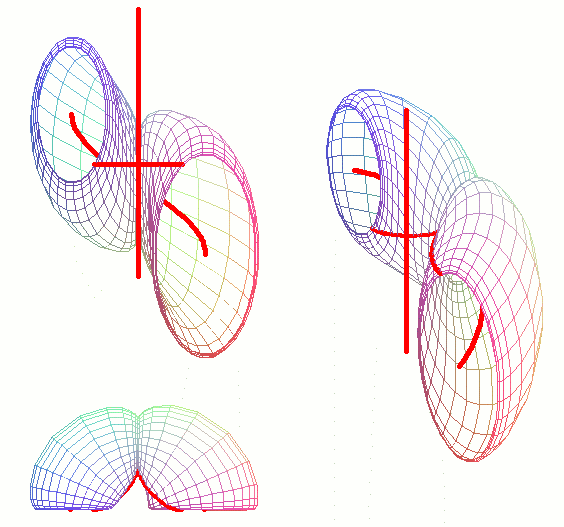
Пример поверхности w-конгруэнции




Вопросы и комментарии к выступлению:
Фото
Селиверстов Александр Владиславович
(5 марта 2017 г. 14:56)

Здравствуйте, Яна Андреевна!
Позвольте задать несколько вопросов о Вашем интересном докладе.
1) Правильно ли, что "эллиптическими линиями" Вы называете эллипсы? Тогда почему бы не написать "винтовыми линиями и эллипсами"? 
Обратите внимание, что существует похожий термин "эллиптическая кривая", который обозначает отнюдь не эллипс, а неособую кубическую кривую на плоскости. 
2) Из доклада не видно, в чём преимущества предлагаемого способа. Если Вы надеетесь, что любые поверхности "в хозяйстве-то как-нибудь под случай понадобятся" (Н.В. Гоголь), то хорошо бы иметь хоть самый простой пример. Может быть элемент детской площадки? Или надувная конструкция?
3) С другой стороны, хорошо бы подробнее описать связь рассмотренных поверхностей с циклидами Дюпена, другими каналовыми поверхностями. Чем отличаются прикладные области, в которых они используются?  
4) Мелочи: в конце аннотации неудачное выражение: "Определены общая структура".
Фото
Кокарева Яна Андреевна
(5 марта 2017 г. 16:59)

Здравствуйте, Александр Владиславович! Спасибо за вопросы и замечания. По поводу "эллиптических линий" меня "терзали смутные сомнения".

На самом деле, этим докладом я в большей мере хотела обратить внимание на сам метод конструирования поверхностей. На то, что из одних и тех же уравнений можно получать три типа поверхностей, содержащие, как минимум, погружаемую линию (то есть какую-то опорную, заранее заданную конструкцию). А сами получившиеся уравнения и поверхности привести в качестве наглядного примера использования этого метода.

Так как я работаю в строительном университете, то, конечно, в первую очередь рассматриваю поверхности с точки зрения архитектурных элементов. И, как Вы правильно заметили, такие винтовые поверхности могут быть использованы в качестве элементов детской площадки. Поверхности пока только получены, поэтому сравнение не проводила, но обязательно в этом направлении поработаю.

С уважением, Кокарева Я.А.
Фото
Гайдарь Олег Георгиевич
(7 марта 2017 г. 23:12)

Здравствуйте, Яна Андреевна!

Интересная статья, близкая и понятная мне по школе И.А. Скидана

Обратил внимание, что Вы единственная из числа учеников И.В. Скидана волею судеб оказавшихся в России и ведущей активную научную работу, по крайней мере, на КГП и пробивающейся в ГиГ. И Вы, безусловно, достойно представляете своего учителя. Есть одно пожелание: более полно знакомить российскую научную общественность с достижениями Скидана и его школы. По вашему перечню ссылок у меня сложилось впечатления что: 1) у Скидана всего два ученика (в том числе и Вы), работающих в данном направлении; 2) у Скидана нет самостоятельного и основательного труда ;3)  много публикаций на украинском языке и в принципе малодоступны в РФ. 4) Скидан не занимался вопросами параметризации и преобразований. Это не так. Было бы понятно, если бы ваши ссылки имели конкретный характер, но в качестве обзорных можно подобрать и более информативные и показательные.  Чем больше у Вас будет ссылок на Скидана И.А. тем лучше для всех его учеников.

С уважением, Гайдарь
Фото
Кокарева Яна Андреевна
(7 марта 2017 г. 23:35)

Здравствуйте, Олег Георгиевич!

Спасибо на добром слове. На самом деле, достаточно сложно вести деятельность в одиночку. К сожалению, мне приходится работать на непрофильной кафедре. И хотя я хорошо общаюсь с заведующим кафедры инженерной геометрии АСА ДГТУ, но в научном плане не удается наладить совместную работу. Поэтому приходится бороться сразу с несколькими факторами: 1) каждый новый семестр я веду новую дисциплину (хотя есть и положительные моменты - я изучаю программирование, а моя дипломница прошлым летом сделала программу по моей диссертации); 2) дипломники; 3) одиночество в плане научного напрвления; 4) маленькая дочка, которую я, к сожалению, даже не имею возможности отдать в детский сад. Поэтому времени и сил на науку остается очень мало. 

По поводу ссылок: пришлось сокращать безбожно, если честно. Конечно, у Ивана Андреевича есть много работ и хороших учеников, но мне тоже сейчас не всё доступно, так как многие материалы в интернете не присутствуют. А я, как Вы понимаете, из дома в чужую страну тоже не могла много забрать...

Написала сюда доклад именно потому, что хочу ознакомить российскую научную общественность с достижениями донецкой школы. Хотя после некоторых комментариев задумалась о том, чтобы написать обзорный доклад по школам прикладной геометрии Украины. Ведь связи теряются, в том числе и из-за языкового барьера.
Фото
Конопацкий Евгений Викторович
(8 марта 2017 г. 12:45)

Здравствуйте уважаемые земляки!

Давайте совместно напишем такой обзорный доклад на следующую конференцию. Я мог бы более плотно познакомить читателей с Мелитопольской школой прикладной геометрии, вы – с Донецкой, ну а остальные школы тогда совместными усилиями.

 
Фото
Кокарева Яна Андреевна
(8 марта 2017 г. 21:16)

Я только "ЗА"! хотя зачем ждать целый год? если есть время, то можно на эту конференцию небольшой обзор сделать. "Пробный". А на следующую (в случае заинтересованности наших российских коллег) в более развернутой форме. Как идея, Евгений Викторович?
Фото
Конопацкий Евгений Викторович
(8 марта 2017 г. 22:58)

Яночка, поздравляю тебя с Международным женским днём! Желаю крепкого здоровья тебе и твоей дочурке! Ещё желаю чтобы "дурной" работы было поменьше, а больше было времени на семью и науку!

На следующий год я предложил потому как выше было сказано, что времени на науку остаётся слишком мало, но я не против сделать такой обзор и в этом году, если у нас будет хотя бы неделя, чтобы мы списались, вычитали информацию друг у друга и т.п.
Фото
Кокарева Яна Андреевна
(8 марта 2017 г. 23:22)

Спасибо, Женя, за поздравления! я постараюсь на выходных выделить время. Если что-то получится, напишу тебе на почту ;-)
Фото
Гайдарь Олег Георгиевич
(8 марта 2017 г. 23:25)

Здравствуйте, Яна Андреевна и с праздником! Любви, Добра и Мира!

Понимаю Ваши трудности, тоже не сахар...

 Раскройте подробности программы по вашей диссертации.

Я так понял, что Вы общаетесь с Александром Витальевичем Замятиным? Милейший человек! Передавайте ему от меня огромный привет.

При оказии не забудьте передать привет и Виктору Федоровичу, Вы ж там рядышком…
Фото
Гайдарь Олег Георгиевич
(8 марта 2017 г. 23:27)

Здравствуйте, Евгений Викторович! Поздравляю Ваших учениц с праздником!

Отличная идея! Попробую подключить к ее реализации Скидана.

Из Вашего обращения к нам «земляки»  напрашивается еще одно предложения: организовать землячество Донбасса. А возглавит его Виктор Федорович, Яна Андреевна обещала устроить.
Фото
Кокарева Яна Андреевна
(9 марта 2017 г. 0:01)

Олег Георгиевич, спасибо )))) Виктор Федорович даже слишком рядом порой ))) наш корпус находится стена в стену с Ростовским судом, куда привозят В.Ф. на видео-допросы. 

С Замятиным общаюсь, привет обязательно передам!

Девочка реализовала алгоритм синтеза уравнений и визуализацию поверхностей конгруэнций прямых, рассмотренных в моей диссертации, в отдельной программе (Delphi + OpenGL). Синтез проходит поэтапно:

1. Выбирается из списка погружаемая кривая (из пространственных и плоских). Пользователь вводит параметры формы и положения кривой, а такжке пределы изменения параметра положения точки на кривой. Здесь же можно посмотреть результат - визуализированное расположение кривой в пространстве.

2. Выбирается конгруэнция, в которую погружается кривая. Задаются параметры конгруэнции. Визуализируется поверхность. Сами уравнения скрыты от пользователя. Из того, что можно сделать с визуализированной поверхностью: поворот, масштабирование, представление каркасом, семействами несущих линий, закрашенной поверхностью, возможность сечения заданной плоскостью (плоскость задается в параметрах A, B, C, D уравнения плоскости, но есть отдельно калькулятор, в котором можно рассчитать эти параметры по уравнению в отрезках и по трем точкам), а также экспорт поверхности в формат .dxf.

Это был диплом бакалавра. Что успели, то сделали. В магистратуру она не осталась.
Фото
Конопацкий Евгений Викторович
(9 марта 2017 г. 20:30)

Очень талантливая девочка, а вы ещё жалуетесь на одиночество в научном плане. Если бы мне программно кто-нибудь так реализовывал все полученные алгоритмы... Хорошие получились у вашей программы возможности.

Интересует возможность построения сечений заданной плоскостью. Может ли ваша программа определить уравнение кривой (или кривых) полученных при сечении плоскостью или в ней просто заложено условие принадлежности точки к плоскости и она лишнее отбрасывает?

 
Фото
Кокарева Яна Андреевна
(9 марта 2017 г. 20:49)

Нет, чисто геометрически ищет пересечение. До уравнений не дошли. Это достаточно сложно, учитывая поэтапную подстановку уравнений. Ведь она не реализовывала символьное исчисление.
Фото
Короткий Виктор Анатольевич
(19 марта 2017 г. 9:36)

Яна Андреевна, как ваши дела? Вы уже получили формулу для расчета числа окружностей в n-мерном пространстве? У меня что-то пока не выходит. А давайте задачу обобщим, займемся чем-нибудь невостребованным! Поставим задачу: вывести общую формулу для расчета числа плоских алгебраических многообразий порядка k (как действительных, так и мнимых) в пространстве размерности n. Заодно ответим на ряд наивных вопросов: может ли быть у мнимой окружности действительный центр? А действительный диаметр? А как указать окружность x2+y2=-R2 на плоскости? Что для этого потребуется, какие графические образы? Более невостребованного трудно придумать. Позовем на помощь Д.В. Волошинова, ребят из Донецка, К.Л. Панчука из Омска. В Омске прекрасно умеют считать параметры. Для них это вообще легко. Получится неплохой такой магический пятиугольник: Питер-Дон-Донецк-Урал-Сибирь. Соглашайтесь! Бензин наш - идеи ваши. Есть плюсы и минусы. Минус - нигде не публикуют. Для математиков - мало математики, для практиков - нет приложений. Спасибо, есть наш профессиональный журнал Г и Г. А в скопусные журналы лучше не соваться. Мало того, что это бизнес, так еще там при регистрации в графе "пол" имеется не две, а три клетки. Тут не то, что руки, а вообще все опустится. Другой минус - если задача затянет, то тогда все, человек пропал. Идиотический блеск в глазах и неспособность ответить на вопрос, который час. Третий минус - не применяются информационно- комм. технологии, ректор не начисляет баллы. И так далее. Перейдем к плюсам. Плюсов нет. Если не считать эфемерную возможность получить счастливый момент истины, когда непонятное вдруг становится понятным, и ты осознаешь, что сделал открытие! Маленькое, но свое. Например, какое-то тысяча первое свойство окружности. Возможно, это будет изобретение велосипеда. Скорее всего, так и будет. Но радость от открытия, от озарения, воспоминание об этом моменте озарения - остается с человеком навсегда. Так что соглашайтесь. Будет что вспомнить. Для начала надо сосчитать число мнимых прямых и мнимых окружностей на комплексной плоскости. А там затянет. Как рассказывал хозяин нового пылесоса: вначале его коту новый пылесос не нравился, а потом ничего - втянулся. С уважением, Короткий В.А  

 

 
Фото
Короткий Виктор Анатольевич
(19 марта 2017 г. 9:54)

Яна Андреевна, в качестве научного руководителя пригласим А.Г.Гирша из Касселя, который про мнимые окружности все знает лучше нас. Получится Международный клуб невостребованной геометрии. МКНГ. Неплохая идея? С уважением, В.А 
Фото
Кокарева Яна Андреевна
(19 марта 2017 г. 12:31)

Спасибо, Виктор Анатольеич, за Ваше "мнимое" предложение. Но в данный момент вынуждена отказать, так как в нашем вещественном мире у меня существует совершенно немнимый муж и немнимая больная четырехлетняя дочь, которые требуют немнимое внимание. Поэтому, если в Вашем ироничном посте есть доля действительности, то мой Вам совет: собирайте команду из мужчин, у которых есть немнимые жены, которые делают за них все немнимые вещи, оставляя им время и возможность заниматься мнимыми вещами в "невостребованной геометрии". 

Еще раз спасибо за предложение! Пойду готовить вещественный завтрак )

Всем хорошего воскресенья!

С уважением, Кокарева Я.А.
Фото
Короткий Виктор Анатольевич
(19 марта 2017 г. 13:03)

Яна Андреевна, не огорчайтесь, все будет хорошо. Все уладится, поверьте. А несерьезное предложение имеет вполне серьезное содержание. Речь идет о кооперации, о научном взаимодействии, о клубах по интересам, которые будут действовать не только во время КГП. Можно очень многому научиться у Д.В. Волошинова, например. Если непонятно - спроси у автора! Связь людей стала очень простым делом. Надо это использовать. Геометрическая лаборатория Д.В. Волошинова - это отчаянный прорыв, попытка вернуться к захватывающе интересному миру проективной геометрии на новом уровне, используя в полную силу компьютерный инструмент для выполнения точных и наглядных ГЕОМЕТРИЧЕСКИХ ЭКСПЕРИМЕНТОВ. Это желание поделиться своими открытиями! Разве это несерьезно? А на шуточную форму не надо обижаться. Вот вполне серьезный адрес OSPOLINA@MAIL.RU. Любые геометрические проблемы - обсудим и решим. Или найдем, к кому обратиться за помощью.

С уважением, Короткий В.А     
Фото
Кокарева Яна Андреевна
(19 марта 2017 г. 13:39)

Спасибо, Виктор Анатольевич! (за "всё будет хорошо" - отдельное). Я буду иметь в виду.

Я.А.
Фото
Бойков Алексей Александрович
(27 марта 2017 г. 23:50)

Здравствуйте, уважаемая Яна Андреевна! Спасибо за доклад. Рад приветствовать на КГП. Будет интересно увидеть продолжение работы и примеры использования поверхностей. Успехов! Отдельное спасибо за второй доклад по украинской школе. С удовольствием бы познакомился с трудами последних десятилетий, недоступными у нас.

С уважением, А.Бойков.
Фото
Кокарева Яна Андреевна
(28 марта 2017 г. 1:03)

Здравствуйте, Алексей Александрович! Спасибо. Обязательно разовью дальше мысль!

Вы напишите, с какими именно работами Вы бы хотели познакомиться, может чем-то смогу помочь. Или хотя бы помочь Вам связаться с автором (все понимают русский). Если нужна такая помощь, то пишите kokareva.ya.a@gmail.com.

С уважением, Кокарева Я.А.

Назад Go Back