КЛАССИФИКАЦИЯ И СТРУКТУРИРОВАНИЕ ЛИНЕЙЧАТЫХ КОНСТРУКТИВНЫХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К КОМПЬЮТЕРНОМУ МОДЕЛИРОВАНИЮ

В работе предложено реализовать решение конструктивных задач компьютерными методами. Для этого проведена классификация конструктивных задач и выявлены их элементарные составляющие – симплексы. Показано, что таких симплексов для линейчатых конструктивных задач существует всего 10.

Конструктивные задачи, наверное, самые древние в истории геометрии. Геометрическими построениями занимались почти все крупные древнегреческие геометры: Пифагор и его ученики, Гиппократ, Евклид, Архимед, Апполоний, Папп и многие другие. Много внимания уделяли конструктивным задачам творцы современной математики: Декарт, Ферма, Ньютон, Паскаль, Эйлер, Гаусс. В XVII-XIX веках разработана теория геометрических построений с помощью различных инструментов, отличных от принятых древними. Датчанин Мор (1672), итальянец Маскерони (1797), француз Понселёж (1813), швейцарец Штейнер (1833), немец Адлер изучали построения, выполнимые циркулем и линейкой, и обнаружили, что циркуль позволяет решить всякую конструктивную задачу, разрешимую циркулем и линейкой и наоборот – только с помощью линейки можно решить всякую циркульную задачу [1]. С конца XIX и по конец XX веков теория геометрических построений сформировалась в обширную и глубоко развитую область математики, связанную с решением разнообразных принципиальных вопросов, уходящих в другие ветви математики.

В XXI веке отношение к конструктивным задачам стало неоднозначным. Многие считают их неинтересными, ненужными и даже надуманными. И в самом деле, где и зачем может понадобиться умение с помощью циркуля и линейки построить правильный многоугольник. С помощью компьютера это можно сделать быстрее, точнее и особенно не напрягаясь [2, 3]. Тем не менее, есть и другая точка зрения, и она неоднократно высказывалась специалистами, в том числе и в рамках данной интернет-конференции [4]. Во-первых, отмечается роль умения решать конструктивные задачи на построения для педагогического и психологического аспектов развития личностных компетенций математиков и инженеров [5]. Во-вторых, Д.В. Волошинов выдвинул идею «создания программных инструментов, которые эмулируют конструктивный геометрический метод» [6]. Эта очевидная и в тоже время неожиданная идея о создании инструментария для геометрического эксперимента [7] вызвала у нас живой интерес и желание рассмотреть конструктивные задачи с точки зрения их программной реализации. Для этого необходимо начать с формализации постановки задачи, классификации и структурирования.

Будем называть конструктивной задачу следующего содержания: Даны фигуры Ф1, Ф2, ..., Фn. Построить фигуру Ф, связанную с фигурами Ф1, Ф2, ..., Фn определенными условиями. Такими условиями могут быть равноудаленность, равнонаклонность, расположение на заданном расстоянии или под заданным углом. Конкретным примером конструктивной задачи может быть следующая: Даны плоскость ∑, точки А и В, прямые l и m. Построить плоскость Г под углом α к плоскости ∑, равноудаленную от точек А, В, прямых l и m.

В зависимости от размерности искомой фигуры конструктивные задачи разделяются на: точечные (искомая фигура – точка), линейчатые (искомая фигура – прямая линия), плоскостные (искомая фигура – плоскость).

В зависимости от характера связей искомой фигуры с заданными фигурами, конструктивные задачи делятся на параметрические и функциональные.

Параметрическими называются задачи, в которых искомая фигура связана с заданными фигурами определенными расстояниями или углами. Например: даны прямые а, b, с, d. Построить прямую l на расстояниях rl, r2 от прямых a, b и под углами α, β к прямым с, d. Параметрические задачи разделяются по характеру параметров на: лонгометрические и гонометрические. Лонгометрической называется задача, в которой в качестве связи выступает заданное расстояние (например, в предыдущей задаче – расстояния r1, r2). Гонометрической называется задача, в которой в качестве связи выступают заданные углы (например, в предыдущей задаче – углы α и β).

Функциональными называются задачи, в которых искомая фигура связана с заданными фигурами равноудаленностью, или равнонаклонностью. Например: Даны точки А. В, С и плоскости ∑ и Г. Построить прямую l, равноудаленную от точек А, В, С и равнонаклонную к плоскостям ∑ и Г. Функциональные задачи разделяются по характеру связи на: эквилонгальные и эквигональные. Эквилонгальной называется задача, в которой в качестве связи выступает равноудаленность. Эквигональной называется задача, в которой в качестве связи выступает равнонаклонность.

Возможны и смешанные задачи – функционально-параметрические.

В зависимости от количества решений конструктивные задачи разделяются на неопределенные, определенные, переопределенные.

Неопределенной называется задача, в которой искомой фигуре - точке, или прямой, или плоскости удовлетворяет множество таких фигур. Например задача, Даны три скрещивающиеся прямые а, b, с. Построить прямую d, пересекающую заданные является неопределенной, так как искомых прямых можно построить множество, которое представляет собой однополостный гиперболоид.

Определенной называется задача, которая имеет конечное число решений. Так, задача Даны четыре скрещивающиеся прямые а, b, с, d. Построить прямую е, пересекающую заданные является определенной, так как число решений является конечным.

Переопределенной называется задача, которая не может иметь решений. Речь идет не об отсутствии решения при определенных расположениях заданных фигур, а о принципиальной невозможности решения. Например, в предыдущей задаче возможны от 0 до 8 вариантов решений. Если же назначить пять скрещивающихся прямых, то построить шестую прямую, пересекающую заданные пять, невозможно. Задача эта переопределена. В ней один параметр (пятая прямая) лишний. Он исключает возможность решения задачи в принципе.

Как же установить по условию задачи, не зная ее решения, переопределена ли она, или определена, или неопределенна? Ответ на этот вопрос дает теория параметризации. Множество точек трехмерного пространства является трехпараметрическим. Следовательно, нужно назначить три параметра, чтобы выделить конкретную точку этого множества. Множество прямых представляет собой четырехпараметрическое множество. Поэтому нужно задать четыре параметра, чтобы выделить конкретную прямую. Множество плоскостей является трехпараметрическим. Следовательно, необходимо назначить три параметра, чтобы выделить конкретную плоскость.

На основании изложенного можно сделать следующие выводы. Если в задаче искомой фигурой является точка, в условии задачи должны быть заданы три параметра. Последние могут быть или расстояниями, или равноудаленностью, либо сочетаниями этих параметров. Следует отметить, что когда речь идет о равноудаленности, то равные расстояния от двух геометрических фигур надо принимать за один параметр. Иными словами, если в задаче необходимо построить точку на заданных расстояниях от точек, то следует назначить три точки; если же необходимо построить точку, равноудаленную от точек, то необходимо задать четыре точки. Это утверждение относится и к линейчатым и плоскостным задачам. Если искомой фигурой является прямая, в условии задачи должны быть заданы четыре параметра. Последние могут быть или расстояниями, или углами, или рав-ноудаленностью, или равнонаклонностью, или сочетаниями этих параметров. При задании трех параметров задача будет неопределенной, пяти – переопределенной. Если искомой фигурой является плоскость, в условии задачи должны быть три параметра. Они могут или расстояниями, или углами, или равноудаленностью, или равнонаклонностью, либо сочетаниями этих параметров. При задании двух параметров задача будет неопределенной, четырех – переопределенной.

Все конструктивные задачи с точки зрения точности построения разделяются на циркульные и нециркульные. К циркульным относятся задачи, в которых решение сводится к построению прямых и окружностей. К ним относятся задачи 1-й и 2-й степени. Степенью задачи называется степень уравнения, к которому сводится аналитическое решение задачи. Если в такой задаче возникает необходимость построения эллипса, гиперболы, параболы, то чертеж необходимо преобразовать коллинейно так, чтобы упомянутые кривые преобразовались в окружность. Прямая же при коллинейных преобразованиях преобразуется снова в прямую. Исключения составляют задачи, в которых возникает необходимость в построении двух кривых второго порядка, не связанных между собой ни общими фокусами (либо фокусом, если это параболы, что чаще и бывает), ни директориальной линией. Например, если в плоскости есть окружность и эллипс, то, преобразуя чертеж так, чтобы эллипс оказался окружностью, мы преобразуем и окружность в эллипс. Поэтому такая задача, хотя и является задачей второй степени, она все же относится к нециркульным. К нециркульным относятся задачи 3-й и выше степеней. Для их решения возникает необходимость построения лекальных кривых или сплайнов. Решение таких задач является приближенным. Точность решения зависит от точности построения кривой (количества взятых точек). Построение последней можно выполнить с наперед заданной точностью, следовательно, и решение задачи можно осуществить с требуемой точностью.

Попробуем разложить конструктивные задачи на «элементарные частицы», т.е. выделим из состава задач их наиболее простые составляющие, которые и назовем симплексами (lat.: простой). Просим не путать с термином симплекс из многомерной геометрии.

Дадим определение: Симплексом называется элементарная графическая операция, которая является составной частью решения конструктивной задачи. Она уже не включает в себя дру¬гие, более простые операции. Симплекс можно сравнить с табличным интегралом, с одной операцией таблицы умножения (например 2×2=4), простыми числами. Симплексы следует воспринимать как табличные интегралы, таблицу умножения и т.п..

Для начала ограничимся рассмотрением только линейчатых конструктивных задач. Существует 10 симплексов для решения линейчатых конструктивных задач [8]. Рассмотрим их.

1с. Расстояние между заданной точкой А и искомой прямой х равно d. Множество прямых х представляет собой комплекс прямых, касательных к сфере с центром в точке А и радиусом d.

2с. Расстояние между заданной прямой а и искомой прямой х равно d. Множество прямых х представляет комплекс прямых, касательных к цилиндру вращения с осью а и радиусом d.

3с. Угол между заданной прямой а и искомой прямой х равен α. Множеством прямых х является комплекс прямых, параллельных образующим конуса вращения Ф с осью а и углом α между образующей и осью а.

4с. Угол между заданной плоскостью Г и искомой прямой х равен β. Данному симплексу соответствует комплекс прямых, параллельных образующим конуса вращения Ф с осью а, перпендикулярной плоскости Г, и углом α=90°-β между образующей и осью а.

5с. Искомая прямая х равноудалена от заданных точек А и В. Множество прямых, равноудаленных от данных точек А и В, представляет собой комплекс прямых, касательных к сферам Фi; и Фj с центрами соответственно в точках А и В и радиусами Ri и Rj, попарно изменяющимися на одинаковую величину. Комплекс состоит из однопараметрического множества конгруэнций. Конкретную конгруэнцию можно выделить из комплекса, если назначить радиусы Ri и Rj равными какой-то конкретной величине. К двум сферам одинаковых фиксированных радиусов можно провести множество касательных прямых, представляющее конкретную конгруэнцию. Последняя, в свою очередь, состоит из однопараметрического множества однополостных гиперболоидов, одного конуса и одного цилиндра.

6с. Искомая прямая х равноудалена от заданных точки А и прямой b. Множеству прямых х соответствует комплекс прямых, касательных к сфере Фi; и цилиндру Фj. Центр сфер – точка А, ось цилиндров вращения Фj – прямая b. Радиусы сфер и цилиндров попарно изменяются на одинаковую величину. Комплекс содержит однопараметрическое множество конгруэнций. Если зафиксировать радиусы сферы и цилиндра какой-то конкретной величиной, выделим из комплекса конкретную конгруэнцию, состоящую из множества касательных прямых к сфере и цилиндру.

7с. Искомая прямая х равноудалена от заданных прямых а и b. Множество прямых х представляет собой комплекс прямых, каса-тельных к двум цилиндрам вращения с осями а и b и равными радиусами, попарно изменяющимися на одинаковую величину. Комплекс состоит из однопараметрического множества конгруэнций. Конкретную конгруэнцию из этого множества можно выделить, если зафиксировать радиусы цилиндров какой-то величиной.

8с. Искомая прямая х равнонаклонена к заданным прямым а и b. Множество прямых х представляет собой комплекс прямых, параллельных плоскостям Г и ∑. Плоскости Г и ∑ образованы биссектрисами углов α и β, стороны которых являются пересекающиеся прямые c и d (с||а, d||b), и перпендикулярами m, n к плоскости Δ(c U d).

9с. Искомая прямая х равнонаклонена к заданным прямой l плоскости Г. Множеством прямых х является комплекс прямых, параллельных образующим конуса Ф. Конус Ф образован следующим образом. Назначим прямую l и плоскость Г (рис. 1). Без ущерба для обобщения изложения, но для упрощения доказательства, зададим прямую l и плоскость Г в положении уровня – прямая во фронтальном, плоскость в горизонтальном положениях. Заметим здесь же, что если в задаче прямая и плоскость будут занимать общее положение, то следует преобразовать чертеж так, чтобы прямая и плоскость заняли положение уровня.

Разделим углы, образованные прямой l и плоскостью Г, пополам. Прямые q и р – биссектрисы этих углов. Точки, лежащие на прямых q и р будут иметь равные расстояния от l и Г. Множество прямых, проходящих через точку S (S= l U Г), на которых находятся точки, одинаково удаленные от l и Г, представляют собой конус Ф. Прямые q и р являются очерковыми образующими конуса Ф относительно фронтальной плоскости проекций. Точка S – вершина конуса Ф, прямая l – его ось.

Проведем горизонтальную плоскость Г (Г₂) на расстоянии h от плоскости Г. Докажем, что плоскость Г рассечет конус Ф по эллипсу.

Построим цилиндр вращения U с осью l и радиусом R=h. Плоскость Г рассечет цилиндр U по эллипсу К. Поэтому эллипс К является множеством точек, равноудаленных от l и Г. Но этим же свойством обладают и точки, образующие сечение конуса Ф плоскостью Г. Таким образом, сечение К конуса Ф плоскостью Г представляет собой эллипс. Отрезок АВ – его большая ось, малая ось CD=2h. Фокусами F^/ и F^// эллипса являются точки касания сфер, вписанных в цилиндр U [9].

Возьмем какую-нибудь образующую m конуса Ф. Все точки этой образующей одинаково удалены от прямой l и плоскости Г. Следовательно, образующая m равнонаклонена к l и Г. Аналогичное можно сказать о любой образующей конуса Ф. Таким образом, все образующие конуса Ф равнонаклонены к прямой l и плоскости ∑. Такое утверждение справедливо и для любой прямой пространства, параллельной какой-нибудь образующей конуса Ф.

10с. Искомая прямая х равнонаклонна к заданным плоскостям Г и Λ. Множество прямых х представляет комплекс прямых, параллельных плоскостям ∑ и Δ. Плоскости ∑ и Δ делят два двугранных угла α а β, образованных плоскостями Г и Λ, пополам.

Все представленные симплексы хорошо известны, но они позволяют решить только весьма ограниченные круг циркульных конструктивных задачи. При этом остается не тронутым огромный пласт нециркульных задач. В последующих работах попытаемся разобраться в методологии решения конструктивных задач 3-й и выше степени.

Список литературы

1. Аргунов Б. И., Балк М. Б. Геометрические построения на плоскости. Пособие для студентов педагогических институтов – М.: Государственное учебно-педагогическое издательство министерства просвещения РСФСР – 1957.

2 Хейфец А.Л. Начертательная геометрия как «бег в мешках» // Проблемы качества графической подготовки студентов в техническом вузе: материалы V Междунар. науч.-практ. интернет-конф. - Пермь: Изд-во Перм. нац. исслед. политехи. ун-та, 2015. - С. 292-325.

3. Хейфец А.Л. Геометрическая точность компьютерных алгоритмов конструктивных задач // Проблемы качества графической подготовки студентов в техническом вузе: материалы V Междунар. науч.-практ. интернет-конф. - Пермь: Изд-во Перм. нац. исслед. политехи. ун-та, 2016. - С. 367-387.

4. Волошинов Д.В. Начертательная геометрия. Есть ли у нее бу-дущее в вузе? // Проблемы качества графической подготовки студен¬тов в техническом вузе в условиях ФГОС ВПО: материалы II Между - нар. науч.-практ. интернет-конф. (г. Пермь, февраль - март 2011 г.). - Пермь: Изд-во Перм. гос. техн. ун-та, 2011. - С. 103.

5. Волошинов Д.В., Соломонов К.Н. Конструктивное геометриче-ское моделировавние как перспектива преподавания графических дисци-плин // Геометрия и графика. - 2013. - Т. 1, вып. 2. - С. 182-185.

6. Волошинов Д.В. О перспективах развития геометрии и ее инструментария. // Проблемы качества графической подготовки студентов в техническом вузе: материалы IV Междунар. науч.-практ. интернет-конф. - Пермь: Изд-во Перм. нац. исслед. политехи. ун-та, 2014. - С. 47-60.

7. Волошинов Д.В. Инструмент для геометрического эксперимента: каким ему быть? // Проблемы качества графической подготовки студентов в техническом вузе: материалы V Междунар. науч.-практ. интернет-конф. - Пермь: Изд-во Перм. нац. исслед. политехи. ун-та, 2015. - С. 111-134.

8. Пастернак Д.Н., Червоненко А.П., Погожельский Г.Ю. К вопросу о конструктивных задачах // Деп. в ГНТБ Украины, №1749 – Ук 93, 07.07.93.

9. Четверухин Н.С. и др. Начертательная геометрия. М.: Высшая школа, 1963, С. 271

Рисунки к докладу

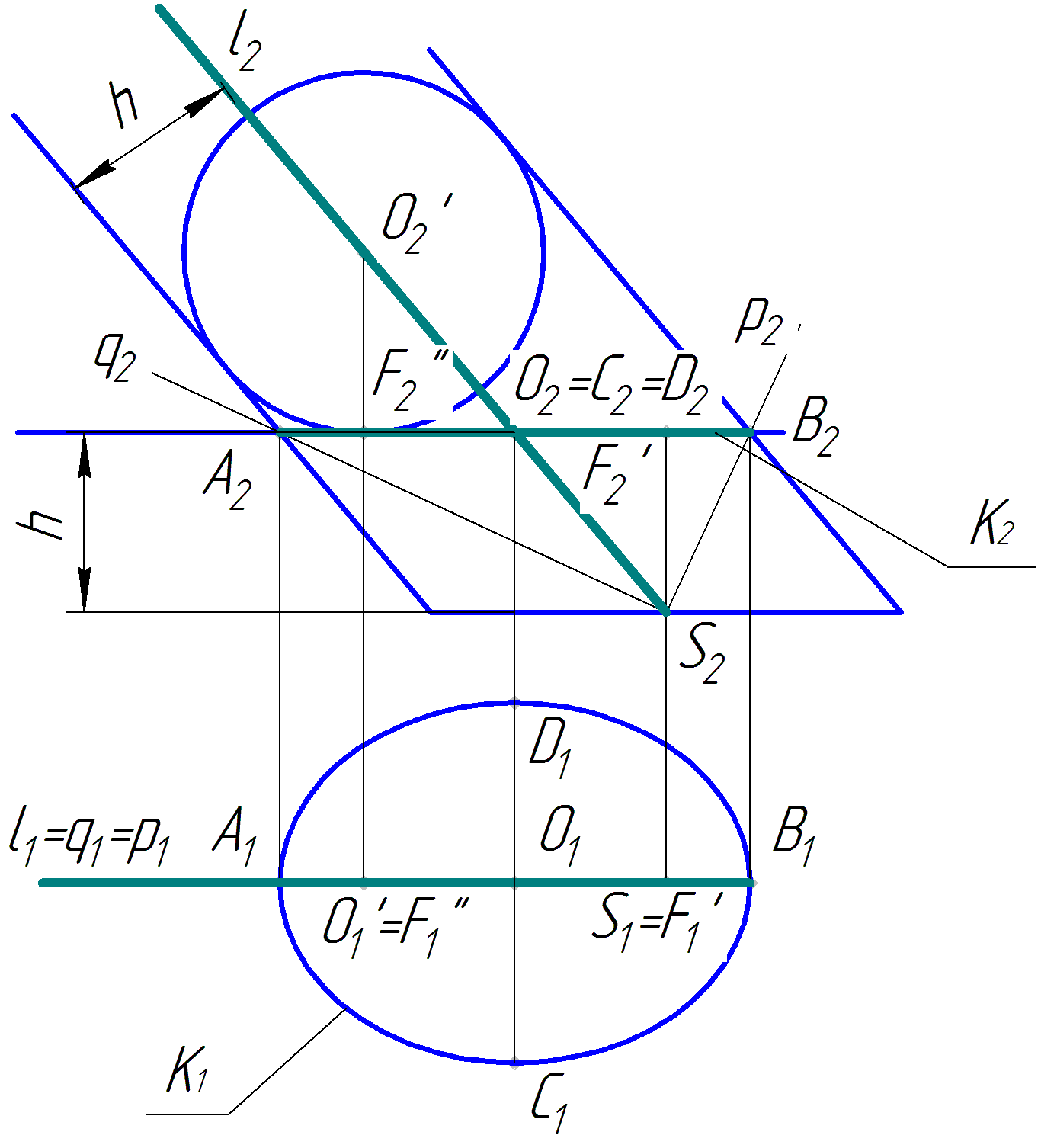
Хейфец Александр Львович (5 марта 2017 г. 0:14)	Олег Георгиевич и Дмитрий Николаевич, я присоединяюсь к словам поддержки и сочувствия, которые были высказаны здесь коллегами. А сейчас к сути Вашего доклада. Прежде всего, уточним определение конструктивных задач. Н.Ф. Четверухин определял конструктивные задачи как те, которые могут быть решены имеющимся набором инструментов (Четверухин, Н. Ф. Методы  геометрических построений: учеб. пособие для пед. ин-тов. М. : Учпедгиз , 1952). В то время, традиционно речь шла  о построениях, выполняемых циркулем и линейкой. Но сейчас к инструментам добавился компьютер с геометрическим программным обеспечением.  Поэтому и определение становится шире. Мое мнение, что сегодня  “конструктивные”  – это задачи на геометрические построения в противовес задачам, решаемым аналитическими методами. Признаком конструктивной задачи является геометрический алгоритм, лежащий в основе ее решения, а также выполнение  геометрических построений при решении.  Циркуль и линейка являются лишь одним из возможных наборов инструментария конструктивных задач, историческим, но далеко не единственным. Потому современные построения - это не только  окружности и прямые линии. Это могут быть поверхности, сложные кривые их пересечения и др. А теперь перейду к причине моего комментария по Вашему докладу. Вы привели две ссылки на мои работы [2,3]. Привели их в негативном плане, в том смысле, что компьютерные технологии, к которым я призываю, отупляют, снижают необходимость мыслить и т.д. И в противовес приводите работы, которые Вы одобряете, хотя в них также предлагаются программные средства решения конструктивных задач. Нелогично. Ваша точка зрения о расслабляющем действии компьютера известна, многократно обсуждалась не прежних конференциях и в публикациях. Она – знамя для тех, кто не владеет современными компьютерными технологиями и находит в ней оправдание. Кстати, а Вы знакомы с AutoCAD’ом – ведь это и есть современные универсально программное средство для решения конструктивных задач, всех тех, которые Вы далее приводите.  Теперь еще раз о том, что компьютер позволяет решать конструктивные задачи не напрягаясь, и что это плохо с педагогического и психологического аспектов. Так решайте соответствующие задачи, которые требуют умственных затрат, а не те, которые Вы привели (“поднимайте планку”). А циркуль и линейка как любимый Вами инструмент для решения – что же, если Вам важен “не результат, а процесс поиска”, пользуйтесь им. Я выступаю за результативность и соответствие современным мировым тенденциям развития геометрического моделирования. И еще о моих работах [2,3]. В них призывы и примеры решения сложных конструктивных задач современными компьютерными 3d методами. Посмотрите еще другие мои работы на эту тему (они приведены в комментариях на поле А.Г. Гирша, кстати, присоединяйтесь к той теме, там как раз о геометрических и аналитических методах). ( или ). С уважением. А.Л. Хейфец.
Гайдарь Олег Георгиевич (7 марта 2017 г. 0:23)	Александр Львович, ждал ваших комментариев! Знал, что вы не «пройдете мимо», но не ожидал, что уделите мне столько внимания. Спасибо! А теперь по порядку. По определению конструктивных задач. На мой взгляд, Четверухин и компьютер - софистика в чистом виде. А в остальном должен согласиться. По негативу. Процитирую сам себя «…где и зачем может понадобиться умение с помощью циркуля и линейки построить правильный многоугольник. С помощью компьютера это можно сделать быстрее, точнее и особенно не напрягаясь [2, 3].» Вы с этим по сути не согласны?  В чем именно заключается «негатив»? Вас смутило «не напрягаясь»?  Так лень двигатель прогресса. «…компьютерные технологии, к которым я призываю, отупляют, снижают необходимость мыслить и т.д.» где вы это нашли в моем тексте? Да, существуют мнения отличные от Вашего. Так бывает. Причем я не даю им оценок, а выражаю свой интерес к конкретной проблеме. Одним словом, вы ищите черную кошку. По «поднятию планки». Вы правы, об этом как раз и сказано в выводах доклада. А теперь перейду на личности. Так вот, лично Вас я считаю одним из наиболее ярких участников КГП благодаря вашей экспрессии. Я всегда с интересом читаю Ваши доклады и комментарии, и даже ознакомился с Вашим учебником. Мало того, я доношу вашу точку зрения у себя на кафедре (помню горячие споры у нас по поводу «…Бега в мешках»), ссылаюсь на Вас на наших местных конференциях. Как бы ни хотелось, но приходится во многом с Вами соглашаться.  И спасибо за приглашение.
Хейфец Александр Львович (7 марта 2017 г. 6:52)	Олег Георгиевич, позвольте два вопроса в связи с Вашим интересным ответом. Первый. О связи определения конструктивных задач в компьютерную эпоху с именем Н.Ф. Четверухина. По-моему, годы прошли, но его определение остается в силе. Если не согласны, можем интересно пообщаться на эту тему. И другие коллеги подтянутся. Термин популярный и для нас важный, но смысл его не всем ясен и трактуют его неоднозначно. Итак, что Вы подразумеваете под конструктивными задачами в связи с компьютерной эпохой в геометрическом моделировании?  А Ваше мнение о термине "геометрическая точность". Неужели только циркуль и линейка?  Второй вопрос. Начиная с 1964 г. в Киеве издавался сборник “Прикладная геометрия и инженерная графика”. Я его весь проштудировал. Это кладезь научной информации по инженерной геометрии. Публиковалась вся страна. И до сих пор (например, в докладе Я.А. Кокаревой на этой конференции), встречаю ссылки на публикации этого сборника. В частности, там много интересных работ нашего Николая Андреевича по сферам Ферма. Однако с 1991 г., ввиду известных событий, издания сборника перестали приходить в Россию. Последний выпуск, пришедший к нам - №51.  Последующих выпусков  нет даже в Москве, в РГБ, проверял недавно. Слышал, что сборник издается и сейчас. Но найти его в наших поисковиках мне не удалось. Если Вам что-то известно, например, сайт этого сборника, где бы можно было посмотреть  электронные варианты текущих выпусков – прошу сообщить. Будет интересно всем. И в целом, продолжает ли действовать киевская школа прикладной геометрии. Какие у Вас конференции, издания. Меня недавно приглашали на одну из украинских конференций – не решился (подстрелят). Где Вы публикуетесь кроме нашего “ГиГ”? А за упоминание моей статьи “… бег в мешках” и моего учебника признателен. Теперь буду говорить, что меня читают и в Донецке. Итак, два вопроса.  С уважением. А.Л. Хейфец
Кокарева Яна Андреевна (7 марта 2017 г. 15:21)	Уважаемый Алеквсандр Львович, насчет сборника "Прикладная и инженерная геометрия", нашла такие ссылки: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?Z21ID=&I21DBN=UJRN&P21DBN=UJRN&S21STN=1&S21REF=10&S21FMT=njuu_all&C21COM=S&S21CNR=20&S21P01=0&S21P02=0&S21COLORTERMS=0&S21P03=I=&S21STR=Ж28584%2F2012%2F90 http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?Z21ID=&I21DBN=UJRN&P21DBN=UJRN&S21STN=1&S21REF=10&S21FMT=njuu_all&C21COM=S&S21CNR=20&S21P01=0&S21P02=0&S21COLORTERMS=0&S21P03=I=&S21STR=Ж28584%2F2012%2F90 Судя по сведениям Национальной библиотеки им. Вернадского, сборник не издается с 2013-го года. К сожалению, остальные номера и/или статьи надо искать только в поисковиках. Гораздо больше шансов найти полные номера по Мелитополю (или статьи в pdf). Или по фамилиям основных представителей школ (Підгорний, Пилипака, Несвідомін, Гумен, Скідан, Ванін и т.д.)
Гайдарь Олег Георгиевич (8 марта 2017 г. 1:13)	Александр Львович, с удовольствием отвечу на Ваши вопросы. 1 Я противник того что бы вырывать из контекста и вольно трактовать слова великих, будь то Четверухин, Монж или Ленин. Они сказали то, что сказали в конкретных условиях, а все остальное это уже слова Хейфеца или Гайдаря. Давать определения я фундаментальных понятий я пока не готов. Вот Ваши определения покритиковать – с удовольствием. :) 2 Ничего не могу Вам сказать о состоянии Украинской науки, начиная с 2014 года. Для нас она закрыта, наверное, даже более чем для Вас. Блокада распространена не только на уголь. Вы не до конца осознали, что Донецк экономически, политически, образовательно  научно и др. ориентирован исключительно на РФ. Многие преподаватели, аспиранты и др. на спец. сайтах (например: Миротворец)  объявлены пособниками террористов с публикацией их личных данных, т.е на Украине их ждет не гипотетическая пуля, а конкретные органы. Что касается довоенного периода (в Донецке свои временные реперы и своя война) то на мой субъективный взгляд специальности 05.01.01. была представлена как минимум не слабее чем в России. Три постоянных докторских совета, общепризнанные научные школы, несколько ВАКовских сборников, ежегодные специализированные очные конференции (самая крупная в Мелитополе), регулярные защиты… Причем в сборниках технические, научные статьи составляли большинство. Минусы этих сборников для россиян в украинском языке, нет регистрации в РИНЦ и отсутствии сайта с эл. версией - распространялись в бумажном виде. Я.А. Кокарева уже дала ссылки и фамилии основателей школ, но и она публиковалась там, потому что еще три года назад была донецкой.
Хейфец Александр Львович (8 марта 2017 г. 7:33)	Олег Георгиевич, приветствую. Прошу привести критику моих определений, о которой Вы обмолвились в п. 1 Вашего ответа. Видимо речь о моих определениях терминов "конструктивные задачи' и "геометрическая точность". Эти термины, на мой взгляд сегодня (да и уже "и  вчера"), требуют корректировки в связи с тем, что основным инструментом в геометрическом моделировании сегодя является компьютер с пакетами 3d программ, а не циркуль и линейка.   Жду критики (или вызываю на "творческую" дуэль ). Мой первый выстрел: сохранение циркуля и линейки как основных критериев в этих терминах сегодня - самооправдание для тех, кому новые методы уже не освоить... А Ваш ответный? По п.2 Вашего ответа - искренне сочувствую. С возрастающим уважением. А.Л. Хейфец
Гайдарь Олег Георгиевич (8 марта 2017 г. 23:22)	Здравствуйте,  Александр Львович! Вынужден отклонить Ваш вызов за отсутствием принципиальных возражений по сути спора. Я толерантен к мнению коллег, и готов принимать любые из них в рамках УК РФ. :) С искренним уважением
Сальков Николай Андреевич (10 марта 2017 г. 10:31)	Александр Львович, а разве в прикладных программах отсутствуют прямые и окружности, что и соответствует так нелюбимым Вами линейке и циркулю?? И разве, чтобы создать некую поверхность, не приходится зачастую их вычерчивать первоначально?
Бойков Алексей Александрович (31 марта 2017 г. 11:17)	Здравствуйте, уважаемые Олег Георгиевич и Дмитрий Николаевич! Спасибо за доклад. Я тоже стою на позиции, что в области геометро-графического образования умение решать задачи, а не нажимать на кнопки - важнее. И мне интересны исследования по теории геомерических построений и решению конструктивных задач. У меня по докладу одно замечание - вы не упоминаете в списке литературы книгу В.В.Глоговского "Элементарные конструктивные задачи по начертательной геометрии". Львов, 1981. С уважением, А.Бойков