

|
Бородкин Николай Николаевич | (Тульский государственный университет ) |
Проведено исследование проявления координатной связи при косом изгибе на примере державки токарного резца, а также исследование процесса формирования сил во взаимосвязи с координатами состояния и траектории движения элементов станка.
Кривые с древних времен привлекали к себе ученых и использовались ими для описания различных природных явлений от траектории брошенного камня до орбит космических спутников и тел.
В настоящей статье проведено исследование кривых (траекторий движения) консольной балки, вала или державки токарного резца при косом изгибе. На наш взгляд наиболее выразительной задачей косого изгиба из выше названных примеров является работа токарного резца. Косым изгибом называется разновидность сложного сопротивления, при которой плоскость действия результирующего изгибающего момента не совпадает ни с одной из плоскостей симметрии поперечного сечения. И в дальнейшем в статье будем рассматривать исследования процесса формирования сил во взаимосвязи с координатами состояния и траектории движения элементов станка на примере токарного резца и его державки.
Процесс резания осуществляется в результате взаимодействия подсистем станка инструмента и заготовки. Это взаимодействие формирует динамическую связь, а сами подсистемы станка объединяются с ее помощью, в результате чего образуется единая динамическая система.
Динамическая система резания рассматривается как единая совокупность управляемых приводов элементов станка, несущей системы, управления, формируемого в координатах состояния, и динамической связи, образующейся в результате взаимодействия инструмента и заготовки.
Современные методы механической обработки характеризуются высокой интенсификацией режимов резания, достигаемой за счет применения хрупких твердосплавных и минералокерамических инструментов, внедрение широкой компьютеризации и автоматизации операций. В этих условиях одним из основных направлений повышения производительности обработки и долговечности работы инструмента стала разработка средств обеспечения устойчивости движения резания – гашение вибраций.
Повышение эксплуатационных характеристик металлорежущих станков и производительности обработки деталей достигается за счет новых инструментальных материалов, выбора рациональных геометрических параметров инструмента и режимов резания, а также выбора оборудования высокой точности и жесткости.
Вместе с тем достижение высокой точности и чистоты поверхности возможно только в том случае, если процесс механической обработки не будет нарушаться вибрациями, т.е. процесс резания будет устойчивым. Однако при работе на металлорежущих станках даже повышенной жесткости, в том числе прецизионных, могут возникать вынужденные вибрации и автоколебания.
Вынужденные колебания могут возникнуть под влиянием периодических возмущений при значительных погрешностях и износе системы привода станка, а также могут передаваться через фундамент от близко работающих, недостаточно уравновешенных станков и двигателей. Поскольку причина возникновения вынужденных колебаний хорошо известна, имеются и достаточные технические возможности для снижения их уровня.
Автоколебания при резании металлов имеют совершенно иную природу. Их появление не связано, с какой либо внешней периодической возмущающей силой. Даже для хорошо отрегулированных станков, обладающих высокой жесткостью, при определенных условиях работы в процессе резания могут возникнуть автоколебания, которые ограничивают допустимые режимы резания, снижают качество изделий, а порой приводят к выкрашиванию режущих кромок инструмента. В отличие от вынужденных колебаний частота автоколебаний остается постоянной в широком диапазоне скоростей резания, что является наиболее характерным признаком, по которому можно отличить вынужденные колебания от автоколебаний [1].
Теоретические и экспериментальные исследования, проведенные в последние годы в области механической обработки металлов резанием, позволили глубже понять многие явления в их взаимосвязи и тем самым способствовали совершенствованию технологии обработки металлов.
Для объяснения природы автоколебаний оказалось необходимым перейти от локальной оценки сил резания и сил упругости к рассмотрению суммарных «базовых» силовых полей, образованных этими силами. Силовые поля ранее рассматривались при исследовании колебаний в «теории координатной связи» В.А. Кудинова, И. Тлустого [1]. Структурная теория автоколебаний с точки зрения создание анизотропных силовых полей ранее не рассматривались, однако, как установлено [2], эти поля существуют и определяют устойчивость станка в процессе резания.
В начале статьи рассмотрим, что такое координатная связь.
Координатная связь проявляется в том, что в общем случае под действием приложенной силы (косого изгиба) вершина резца стремится сместиться не только в направлении вектора силы, но и в ортогональном направлении. Это происходит из-за того, что жесткость инструментального узла – балки различна для разных направлений, т. е. существуют главные оси жесткости, которые обычно не совпадают с координатными осями станка.
Статические жесткости С1 и С2, измеренные в направлении этих осей, различны (С1>С2). Любой вектор силы, приложенной к инструменту, может быть разложен по главным осям. В результате составляющие перемещений по главным осям и будут обратно пропорциональны соответствующим жесткостям С1 и С2. Это приводит к тому, что угол, определяющий направление полного смещения вершины инструмента не совпадает с углом, определяющим направление действия силы. Если взять единичную силу и проварировать угол γ от 0 до 360°, фиксируя результирующие смещения, можно получить эллипс полного смещения (рис. 1). Точки 1,2,3 и 4 это траектория колебания (движения) вершины резца, как наиболее слабого в подсистеме резец-заготовка. Вид этого эллипса целиком определяется конструктивными особенностями упругой системы в окрестностях инструментального узла [1].
Описанная в упрощенном варианте анизотропия упругой системы на плоскости на самом деле существует в пространстве и приводит к тому, что при нагружении резца силой, параллельной скорости резания, его вершина смещается не только в тангенциальном направлении, но и в каком-то ортогональном (радиальном при рассмотрении смещений на плоскости) направлении. И очень влияет на точность и шероховатость обработанной поверхности.
В результате анализа работы резца при косом изгибе и исследования влияния координатной связи напрашивается вывод, что необходимо при точении уменьшать проявление координатной связи.
До настоящего времени было проведено большое количество исследований в области изучения «теории координатной связи» при точении и других видах обработки. При этом установлено, что главными причинами возникновения координатной связи в подсистеме «инструмент - заготовка» являются:
До настоящего времени остается нерешенной проблема повышения виброустойчивости процесса точения на основе снижения уровня проявления координатной связи. При этом известно, что устранить автоколебания, связанные с проявлением координатной связи, можно на основе ориентации жесткости и диссипации наиболее слабого звена технологической системы (резца) по направлению результирующей силы резания [1]. Реализовать при точении рациональную ориентацию осей жесткости подсистемы инструмента как наиболее слабого звена технологической системы по направлению равнодействующей силы резания для существующих конструкций резцов практически невозможно, а соответственно нельзя устранить автоколебания, связанные с проявлением координатной связи. В связи с этим повышение виброустойчивости токарной обработки на основе снижения уровня проявления координатной связи можно обеспечить путем применения токарных резцов со структурированными державками, обладающими анизотропной жесткостью.
Для этого рассмотрим формирование анизотропных силовых полей при работе токарного резца. Физический смысл анизотропных силовых полей, образованных силами упругости, силами резания и демпфированием принципиально отличается от поля напряженного состояния в срезаемом слое металла или от поля напряжений на рабочих поверхностях инструмента.
В процессе резания пластинка твердого сплава, припаянная или закрепленная прихватом к державке резца, находится в равновесии под действием двух сил: силы резания Р0 и силы упругости Т0.
Сила упругости возникает при деформации системы резец – суппорт и уравновешивает силу резания, т.е. она равна ей и противоположно направлена; только в этом случае возможно состояние равновесия пластинки твердого сплава, которое наблюдается в спокойном, безвибрационном процессе резания.
Если случайные факторы выведут резец из состояния равновесия (например, резец переместится в радиальном направлении и при этом увеличится глубина резания), изменится сила резания на некоторую величину Р, также и сила упругости получит приращение Т . Очевидно, что если бы приращение силы резания было точно равно и противоположно приращению силы упругости, то установившейся режим резания наступил бы и в новом отклоненном положении резца. Однако сила резания и сила упругости, по мере отклонения резца изменяются по разным законам, и новое значение силы резания не уравновешивается новым значением силы упругости (рис.2).
Суммируя приращение силы резания и силы упругости, возникающие при отклонении резца из положения равновесия можно получить векторную структуру приращений сил, под действием которой оказывается система резец - суппорт при случайном нарушении процесса резания. Для построения векторной структуры силового поля надо знать характеристику силы резания, а также закон изменения силы упругости (жесткость упругой системы резец – суппорт по главным осям С1 и С2)
С физической точки зрения поле напряженного состояния и векторное силовое поле принципиально различны. Эпюра напряжений и траектории главных напряжений отражают одновременно фактическое напряженное состояние в каждой точке поперечного сечения исследуемого образца.
Силовое поле, хотя и указывает на направление силы в любой точке окрестности положения равновесия, однако, фактически на точку, отклоненную из положения равновесия с координатами Х1 и Х2, действует в любой момент времени лишь одна определенная сила, модуль и направление которой определяются зависимостями:
Т1=-С1Х1 ; Т2=-С2Х2 ; (1)
По составляющим Т1 и Т2 можно построить силу упругости в любой точке в окрестности положения равновесия. Если определить и построить достаточно много сил, нетрудно затем провести силовые линии, т.е. такие линии, в каждой точке которых силы поля являются касательными. Это построение выполнено на рис.3. Для случая С2 =2С1 . Количество силовых линий может быть выбрано произвольно, однако, независимо от того сколько построено силовых линий, они дают общее представление о структуре силового поля. В рассматриваемом случае силовые линии представляют собой семейство парабол, причем все силовые линии проходят через начало координат.
Можно ли сравнить силовое поле, построенное таким образом, с полем напряженного состояния деформированного образца металла, например вала, нагруженного крутящим моментом? В поперечном сечении вала можно построить эпюру главных касательных напряжений, а затем траектории главных напряжений – сплошные линии, в каждой точке которой главные напряжения будут направлены по касательной.
Хотя траектории главных напряжений и силовые линии обладают тем общим свойством, что касательные к этим линиям определяют направление главного напряжения или направление силы, однако физически поле напряженного состояния и силовое поле принципиально различны.
Эпюра напряжений и траектории главных напряжений отражают одновременно фактическое напряженное состояние в каждой точке поперечного сечения вала.
Таким образом, силовое поле физически не тождественно с полем напряженного состояния.
С механической точки зрения поле силы упругости отвечает основному определению силового поля как области, в каждой точке которой действует сила, зависящая только от координат этой точки.
Уравнение силовых линий для такого поля выводится из определения понятия силовой линии, согласно которому касательная к силовой линии в любой ее точке совпадает по направлению с силой поля.
Если силовую линию в плоскости Х1 Х2 определять радиус-вектором
r = r (X1 X2)
То дифференциал радиус-вектора dr и вектор силы T будут совпадать по направлению, а значить их проекции на оси координат будут пропорциональны.
dX2/dX1 =T2/T1 (2)
Исходя из этого уравнения, можно построить силовые линии аналитическим путем. Так для рассматриваемого примера материальной точки на упругих связях, учитывая значения (1) и (2), запишем
dX2/dX1 =C2 X2/C1 X1 = 2X2/X1
Интегрируя, найдем
. Х2 = BX12
Задаваясь рядом значений произвольной постоянной В, можно построить ряд интегральных кривых – силовых линий (рис.3).
Таким образом, силовое поле дает представление о направлении сил, действующих на точку, поддерживаемую упругими связями, когда она выведена из состояния равновесия.
Как известно, с целью математического анализа устойчивости станка в процессе резания упругая система резец – суппорт может быть представлена в виде приведенной расчетной схемы (рис.4) , где ç1 и ç2- главные оси жесткости, C1 и C2 - жесткость эквивалентных пружин. Масса системы приводится к вершине резца, а упругие свойства системы, характеризуются двумя пружинами, направление которых совпадает с направлением главных осей жесткости.
Векторную структуру силового поля (направление сил поля в окрестности вершины резца) определяет устойчивость процесса резания [1] , для этого рассмотрим векторное поле упругости в окрестности вершины резца. Пусть жесткость пружин C1 и C2 известна и начало координат принято в положении вершины резца. При этом масса системы приводится к вершине резца, а упругие свойства системы характеризуются двумя пружинами, направление которых совпадает с направлением главных осей жесткости. Главные оси жесткости в отличие от других осей, проходящих через вершину резца, имеют особенность, что перемещение под действием силы, приложенной в направлении любой из главных осей, точно совпадает с этим направлением. Так, под действием силы резания, приложенной к вершине резца, перемещение ее будет иметь как вертикальную, так и горизонтальную составляющую, т.е. результирующее перемещение не будет совпадать с направлением приложенной силы.
Жесткость по направлению главных осей определяется на основании статических испытаний. Так по данным [1] для станка модели 1А62 при вылете резца 35 мм параметры приведенной системы резец – суппорт следующие: C1=2.4 x103 кГ/мм, C2 = 7.4 x103 кГ/мм, координаты центра жесткости Х10 =111 мм, Х20 =111мм, .
Определим проекции силы упругости на главные оси жесткости
T1ç =-ç1C1 ; T2ç =-ç2C2
Если силовую линию в плоскости X1 X2 определять радиусом вектором r , то дифференциал радиус - вектора dr и вектор силы T будут совпадать по направлению, а значить их проекции на оси координат будут пропорциональны.
dX2/dX1 =T2/T1 ;
Дифференциальное уравнение силовых линий будет
dç2/ dç1 =T2ç / T1ç=C2ç2 /C1ç1
Проинтегрируем и выразим ç2
ç2 =Bç1C2/C1 ;
Согласно примера, [1] расчетной схемы упругой системы резец – суппорт жесткость по главным осям известна и уравнение силовых линий запишется .
ç2 =Bç13.08 ;
Задаваясь рядом значений постоянной В на рис. 4. построено семейство силовых линий – векторное силовое поле в окрестности положения равновесия. Это поле физически определяет лишь направление силы упругости в случае, когда система будет выведена из состояния равновесия. Однозначно напрашивается вывод, чтобы обеспечивать асимптотическую устойчивость консольной части резца в процессе точения, необходимо чтобы кривые базовых полей проходили через вершину, а не двигались по эллипсу.
Приведенный анализ показывает, что для обеспечения асимптотической устойчивости системы в целом требуется следующие конструктивные изменения в режущем инструменте. Необходимо сконструировать инструмент таким образом, чтобы варьировать в пространстве его упругие и диссипативные свойства, т.е. попытаться создать конечномерную динамическую многослойную структуру державки резца на примере [5]
Таким образом, чтобы уменьшить влияние проявления координатной связи необходимо создать консольную часть державки резца с направленной жесткостью по главным осям (С1>С2). Причем в направлении жесткости С2 создать вязкоупругую реологическая структуру с высокими демпфирующими свойствами, например модель Фойгта [3].
В данной анизотропной структуре консоли формирование векторного силового поля (парабол) будут ориентированы относительно оси С1 и не менять своего положения. Пространственная траектория движения вершины резца в процессе точения будет осуществляться не по эллипсу (проекции на плоскость), а по пространственным кривым, проходящим через вершину резца.
В работе [5] показана многослойная конструкция токарного резца с использованием металлических пластин и демпфирующего слоя, например, металлической пены. Кроме металлической пены можно использовать композит или композиционный материал с высокой адгезией с металлом.
На самом деле влияние координатной связи на подсистему существует в пространстве и приводит к тому, что при нагружении резца силой, параллельной плоскости резания, вершина смещается не только в тангенциальном направлении, но и в радиальном, образуя траекторию движения - пространственный овал. При использовании резца данной конструкции происходит демпфирование консольной части в направлении жесткости С2 , что препятствует образованию пространственного овала.
При токарной обработке вершина резца находится в условиях всестороннего сжатия. Силы, препятствующие движению резца, кроме тангенциальных, стеснены и определяются силами реакции со стороны адгезионных мостиков [1], и силами реакции со стороны образующейся стружки, сопротивляющейся отжиму и ортогональному перемещению инструмента.
Согласно траектории движения консоли (рис. 1 ) происходит формирование колебательных (циклических) движений вершины резца, возникающих с участием координатной связи. Упругая система (УС) резца накапливает энергию во время движения. Причем чем больше траектория движения, тем большей энергией запасается УС и, следовательно больше амплитуда обратной траектории. С энергетической точки зрения количество потенциальной энергии, накопленной при движении вершины резца за один проход по эллипсу, определяется силами, необходимыми для создания упругих и пластических деформаций стружки и материала заготовки и зависящими от режима резания, износа инструмента и физико-механических свойств обрабатываемого материала. Указанная потенциальная энергия [2] обратно пропорциональна жесткости УС и определяет амплитуду автоколебаний при возбуждении.
При точении резцами с многослойными державками с направленной жесткостью (рис.4) интенсивные автоколебания не возникают т.к. потенциальная энергия расходуется (релаксирует) малыми порциями и с более высокой частотой, что позволяет потенциальной энергии не накапливаться в УС.
При точении резцами со стальными державками потенциальная энергия накапливается больше и релаксируется более большими порциями в УС, создавая большую амплитуду колебаний.
Диаграмма перемещений вершины резца с державками из наклонных многослойных конструкций представляет собой не сплошной эллипс упругой системы суппортной части станка, а эллипс с элементами демпфирования УС или эллипс с разрывом в виде демпфера [4].
Таким образом, рассматривая сравнительные колебательные движения вершины резца со стальной и комбинированной державками, возникающих с участием координатной связи, опасность возникновения автоколебаний с большой амплитудой заключается не в количестве накопленной энергии, а в ее релаксации большими порциями, что более характерно для стальных державок резцов.
Амплитуда колебаний нарастает до тех пор, пока не наступит равенство энергий самовозбуждения колебаний, создаваемого процессом резания, с возрастающей энергией рассеяния. Тогда установятся стабильные автоколебания с частотой, определяемой свойствами упругой системы. В следствие координатной связи где изменяются динамические характеристики резания по главным осям из-за конструкции державки в системе изменяется траектория движения резца и заготовки, система оказывается более устойчивой.
Наиболее негативные последствия обусловлены автоколебаниями с траекториями, ориентированными преимущественно в радиальном направлении. Тангенциальное направление меньше влияет на увеличение шероховатости обработанной поверхности.
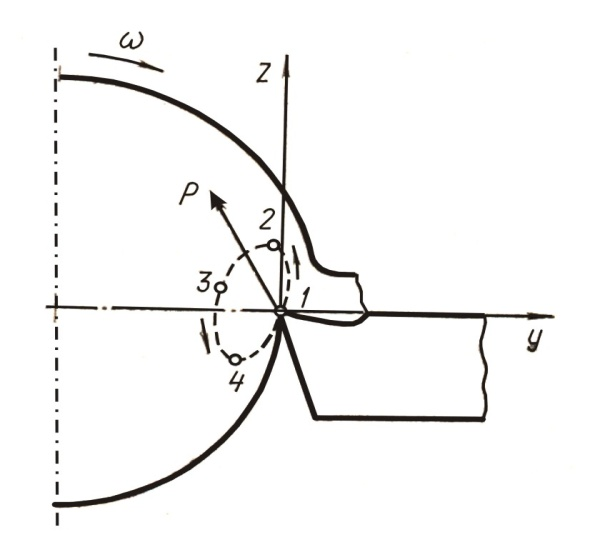
Траектория относительного движения резца и заготовки
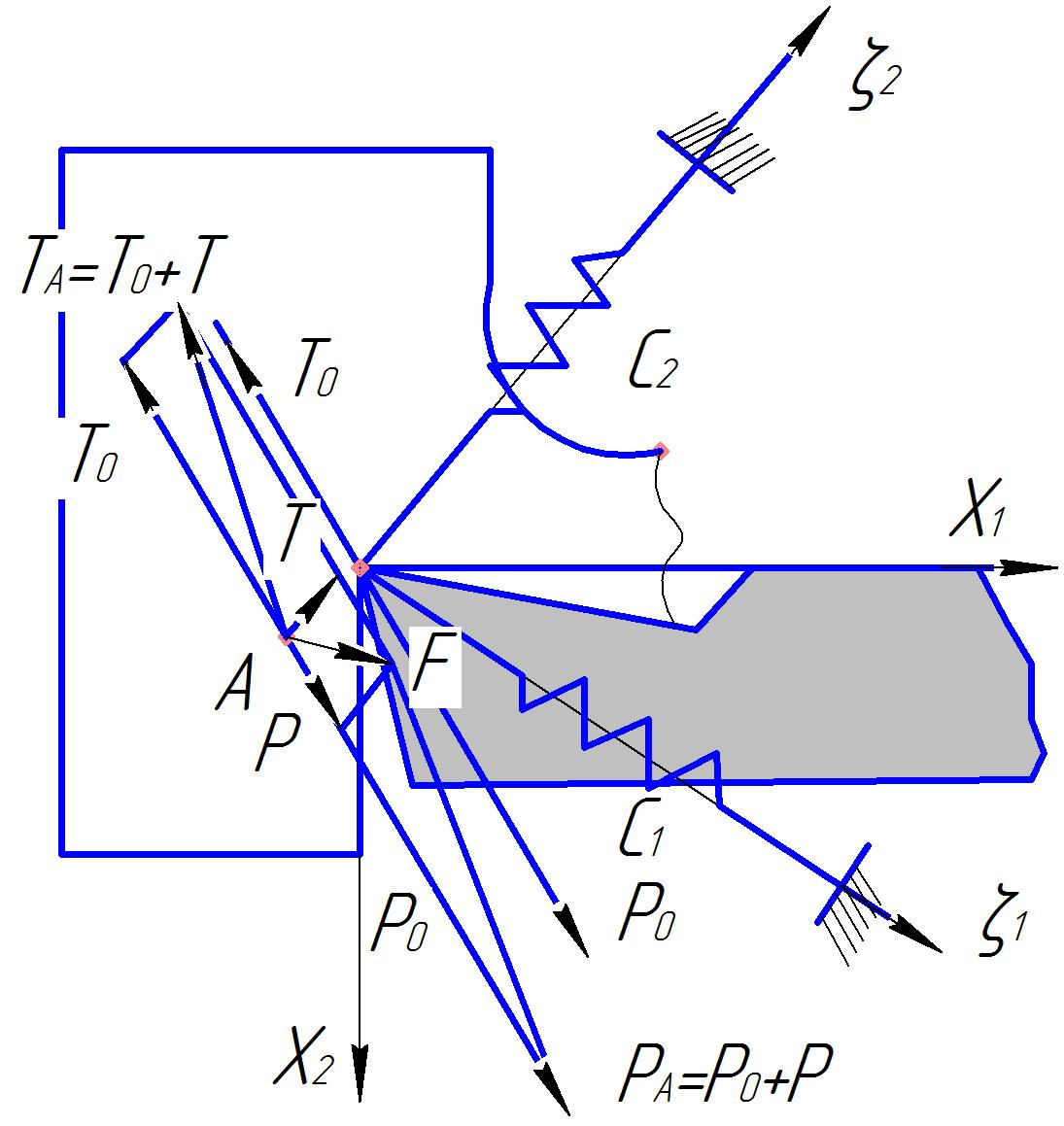
Образование силы базового поля F в окрестности вершины резца
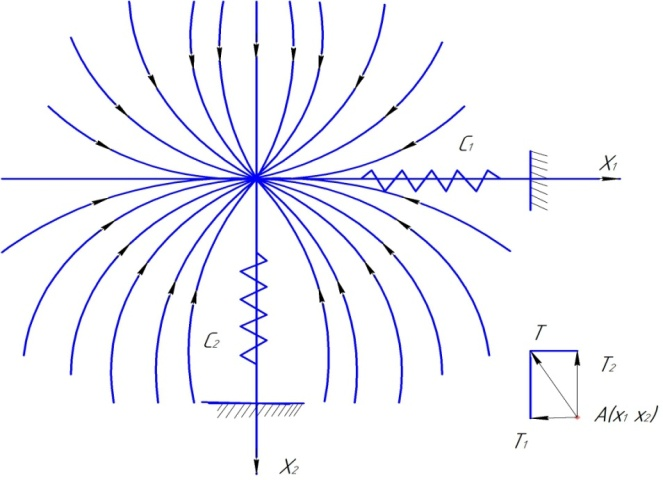
Поле силы упругости в окрестности положения равновесия (С2 =2С1) консоли
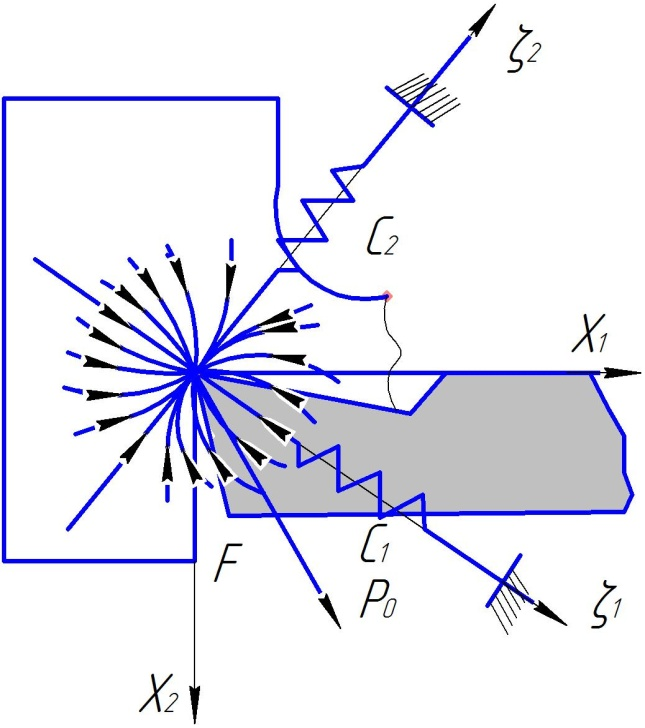
Поле силы упругости в области вершины резца

Тихонов-Бугров Дмитрий Евгеньевич (15 марта 2017 г. 14:07) |
Николай Николаевич, здравствуйте! Вносит ли какие-нибудь особенности в расчёты конструкция станка, например, классический токарно-винторезный и ЧПУ? С уважением, Тихонов-Бугров. |

Короткий Виктор Анатольевич (15 марта 2017 г. 14:42) |
Уважаемый Николай Николаевич! При исследовании автоколебаний и вообще при исследовании устойчивости какого-либо процесса должна быть выявлена обратная связь, составлена система (нелинейных) дифф. уравнений, устойчивость решения которой в данной точке исследуется, после линеаризации, с помощью известных в теории САУ критериев. Для наглядности составляется блок-схема с указанием обратной связи и ее коэффициентом усиления. И так далее. Может быть, Вы не ставили задачу исследования устойчивости системы СПИД? С уважением, Короткий В.А |

Бородкин Николай Николаевич (15 марта 2017 г. 17:57) |
Уважаемый Дмитрий Евгеньевич, здравствуйте! Большое спасибо за внимание и интерес к статье. В статье раскрывается что такое "координатная связь" и ее влияние на формирование суммарных базовых силовых полей в процессе точения резцом, как наиболее слабого звена ТС станка. В статье приводятся расчеты по формированию силовых полей и показано, что направление этих полей зависит от направлений максимальной и минимальной жесткостей при косом изгибе. Особенность в расчетной части конструктивных элементов станка очень зависима. Расчеты в зависимости от режимов резания, видов резца, его сечения и т.д. по конструктивным особенностям станка и видам в статье не приводятся. Так как эти вопросы больше интересуют технологов, конструкторов. С уважением Бородкин Н.Н. |

Бородкин Николай Николаевич (16 марта 2017 г. 18:02) |
Уважаемый Виктор Анатольевич, Здравствуйте! Выражаю Вам благодарность за внимание и интерес к статье. Да Вы правы при исследовании автоколебаний и вообще при исследовании устойчивости какого-либо процесса должна быть выявлена обратная связь, составлена система (нелинейных) дифф. .. и т.д. Исследования координатной связи предшествующих авторов (Кудинова В.А., И. Тлустый и т.д. их более 50 ) при изучении механизмов потери устойчивости использовали скалярные модели зависимости сил от координаты упругих перемещений. В статье мы рассматривали векторное представление зависимости сил от деформационных смещений. Векторное представление процесса точения и виброустойчивости СПИД в целом дает более ясное представление о влияние координатной связи. Существует несколько причин возбуждения и развития автоколебаний при точении, одной из которых является наличие координатной связи. При этом автоколебания инициируются, как правило, наиболее слабым звеном технологической системы, роль которого часто выполняет режущий инструмент. При этом известно, что устранить автоколебания, связанные с проявлением координатной связи, можно на основе ориентации жесткости и диссипации наиболее слабого звена технологической системы по направлению результирующей силы резания. Реализовать при точении рациональную ориентацию осей жесткости подсистемы инструмента как наиболее слабого звена технологической системы по направлению равнодействующей силы резания для существующих конструкций резцов практически невозможно, а соответственно нельзя устранить автоколебания, связанные с проявлением координатной связи. Принципиальную важность можно отметить в том, что координатная связь может при благоприятном устройстве системы вызвать нарастающие (самовозбуждающие) колебания системы (рост эллипса) или поддерживаться на нежелательном уровне, что характерно для изотропной структуры в подсистеме инструмента. Для анизотропной структуры упругая система при С1 /С2 >2 и более приобретает минимальную линейную зависимость (статическую характеристику) от угла , в этом случае не учитывается влияние (менее зависима) замкнутости динамической системы и исключается влияние деформации суппорта на точность обработки. Т.е. Упругая система СПИД и процесс резания формирует динамическую систему с обратной связью и если удается управлять по направлениям, то мы можем достигать наибольшую жесткость и диссипацию по направлениям. Что в конечном итоге дает повышение виброустойчивости, соответственно повышение качества обработке и т.д. С Уважением Бородкин Н.Н.
|