УЧЕБНОЕ ЗАДАНИЕ “ПРОСТРАНСТВА РАЗЛИЧНОЙ РАЗМЕРНОСТИ”

Рассмотрены варианты учебных заданий по начертательной геометрии с использованием отображения пространств различных размерностей друг на друга. Даны примеры выполнения заданий.

Пространство трехмерно. Оно содержит три измерения – длину, глубину, высоту. Это знание присуще человеку, его не надо объяснять. Дальше этого наши бытовые знания не идут. У человека нет необходимости особо вникать в смысл понятия “пространство”. Да, мы знаем из популярных передач и из сенсационных видеороликов в Ютюбе, что у физиков остался только один нерешенный вопрос: наше пространство 6-мерное или 7-мерное? А так все остальное им понятно. Может быть, физики шутят? К тому же наше пространство несколько искривлено. Это было теоретически установлено А. Эйнштейном и подтверждено экспериментально еще в начале 20 века.

На самом деле физически, реально существует только трехмерное пространство. В масштабах повседневной человеческой деятельности оно не искривлено. Это линейное пространство, в котором прекрасно выполняются постулаты Евклида, включая пятый. Но что означает термин “линейное пространство”?

В любом деле один вопрос всегда тянет за собой массу других вопросов. Если есть линейное пространство, значит, есть нелинейное? Если есть трехмерное, значит, есть и  пространства других размерностей? Конечно, есть. Начертательная геометрия – это раздел не физики, а математики, поэтому мы имеем право рассматривать физически невозможные пространства различной размерности – как больше трех, так и меньше одного. Например, точка – пространство нулевой размерности. Не надо путать с нуль-пространством из голливудской фантастики.

Итак, чуть только мы заговорим о структуре пространства – сразу появляются вопросы. Где больше точек – на прямой или на плоскости? Где больше прямых – на плоскости или в пространстве? Почему линию (хоть плоскую, хоть пространственную) называют одномерным пространством, а поверхность – двумерным? Ведь они находятся в трехмерном пространстве! Почему линейчатую поверхность называют криволинейной, если на ней превосходно размещаются прямые линии? Ведь она линейчатая, а значит – линейная. Разве не так? Сколько линейных двумерных пространств в трехмерном? А нелинейных? Как сосчитать? Как сосчитать число окружностей на плоскости? А в пространстве? Что такое гиперсфера, гиперкуб?

Эти вопросы не придуманы, они взяты из форумов в Интернете. Скорее всего, они инициированы преподавателями математики, а не геометрии. Но вопросы – геометрические! Кто должен отвечать на эти и многие другие подобные вопросы? Кажется, это именно наша специализация, это ГГП, общеобразовательный курс. Почему, например, на бесконечно длинной, ничем не ограниченной прямой ровно столько же точек, что и на маленькой ограниченной дуге окружности? Как грамотно, четко, наглядно отвечать на такие вопросы?

Может быть, на вопрос о размерности кривой линии не надо отвечать, потому что не востребовано? Да и насчет количества точек. Какая разница, сколько их там. Пусть математики отвечают. Но ведь кафедра графики, как и математики, относится к общеобразовательному циклу! Как и кафедра литературы, истории. Скажите, будет востребовано знание истории эпохи Возрождения в будущей профессиональной деятельности инженера-конструктора? А Онегин? Будет востребован? А комплексные числа? Да кто их вообще видел, эти комплексные числа? А мнимые точки? Час от часу не легче.

Конечно, можно сказать, что математика обязательно востребована, значит, и комплексные числа тоже востребованы. Это да. Учить комплексные числа надо. А вот мнимые точки не надо. Они не нужны. Невольно вспоминается герой одного из романов М. Булгакова, который с осуждением относился к котам, но слонов одобрял, потому что слоны (ну и комплексные числа) – это животные полезные. То есть востребованные. А всякие там коты и мнимые элементы – нет. Зачем их в квартиры и в геометрию пускают?

Хватит повторять мантру о невостребованности общегеометрических знаний! Может быть, будет не совсем бесполезно, если мы высвободим в учебном плане немного времени от просмотра слайдов на лекциях по НГ и от бесконечного 3D-моделирования на уроках компьютерной графики и от моделирования корзинок на олимпиадах, а используем это время на другие вещи, не входящие в список компетенций по ФГОС 3 плюс? Конечно, если ректор узнает – нам не поздоровится.

Задание 1. Понижение размерности пространства с R³ до R²

Как отобразить фигуры трехмерного пространства на плоскости или на любом другом двумерном пространстве? Этот вопрос давно решен. В 16 веке была разработана теория перспективы, в 18 веке – аксонометрия и незаменимый в практических приложениях эпюр Монжа. Не случайно появление эпюра Монжа совпало по времени с промышленной революцией. Эти три способа отображения пространства на плоскость построены по единому методу “двух изображений”, когда любая точка на чертеже указана двумя своими проекциями [1].

В конце 20 века аксонометрические (и перспективные) проекции стали широко применяться в компьютерной графике для отображения на экране компьютера геометрических фигур, хранящихся в цифровой матричной форме в недрах винчестера. При этом возникла некоторая терминологическая путаница. Электронная модель изделия (ЭМИ) – это то, что существует исключительно в цифровом виде, в двоичном коде, в матрицах. То, что мы видим на экране, тоже ошибочно стали называть электронным макетом, или 3D-макетом. Это совершенно неверно. Это грубейшая терминологическая ошибка, которая привела нас в тупик и стала препятствием на пути развития ГГП. Гипертрофированное почтение к аксонометрическому изображению на экране как к какой-то панацее во всех конструкторских делах привело к пересмотру учебных планов ГГП вплоть до отказа от технического чертежа и фанатичных попыток ставить размеры прямо на аксонометрии! Только бы не двухпроекционный чертеж! Ведь он устарел! И на Западе не используют.

На экране монитора мы видим именно проекционный чертеж! Мы видим аксонометрическое изображение электронного макета изделия! Меняя точку зрения, мы получаем либо центральную, либо параллельную аксонометрию. Это чертеж! На экране монитора – двухпроекционный аксонометрический чертеж фигуры. Этот чертеж условно называют 3D-макетом только для краткости речи! На самом деле 3D-макет – это матрицы координат характерных точек фигуры, а также матрицы, содержащие коэффициенты уравнений, описывающих линии и поверхности фигуры. Не надо отождествлять электронный макет фигуры (цифровую матрицу) и изображение этой фигуры, полученное на основе электронного макета. Объект – это матрица, изображение – аксонометрия на экране компьютера. Все кнопочные команды воздействуют не на экранный чертеж, а на электронную модель, то есть на цифровую матрицу. А аксонометрическое изображение на экране послушно следит за изменением модели.

Основной вопрос и основная тема задания 1 – чертеж. Как отобразить фигуру трехмерного пространства на двумерное пространство без потери информации? Ведь мы фактически теряем одно измерение. Чем компенсировать эту безвозвратную потерю? Ответ дает метод двух изображений.

Главная тема задания 1 - показать и доказать полное равноправие перспективного, аксонометрического и ортогонального чертежей. В том числе – пресловутые аксонометрические изображения на экране монитора, которые в целях сокращения слов кто-то когда-то назвал “3D-графикой”. С тех пор так и пошло. Все эти варианты отображения пространства на плоскость построены по методу двух изображений. И совершенно неважно, на каком носителе физически реализовано это отображение – на песке палочкой или на экране мышкой.

Да, безусловно, ревнители компетенций возразят, что перспектива – это нам не надо. Это для архитекторов и строителей. Для инженеров не предусмотрено ее изучение. Тогда как быть с теми студентами автотракторного факультета, которые на лекциях по НГ, пока преподаватель крутит слайды, рисуют машинки в перспективе? Причем с удивительно точными перспективными сокращениями! Кто им объяснит теоретическую базу перспективного изображения? Так и не будут знать, что “говорили прозой”.

Остановите слайды и видеопрезентации, не надо готовых картинок! Просто объясните, что метод двух изображений универсален, что иначе просто никак не отобразить трехмерное на двумерное. Мы понижаем размерность образа по сравнению с размерностью точечного прообраза, и обязаны это компенсировать либо двумя проекциями на чертеже Монжа, либо вторичными проекциями всех точек изображаемой фигуры в аксонометрии – центральной или параллельной. У нас просто нет выбора.

Дайте студенту задание номер один: изобразить простой русский кирпич в трех вариантах – на чертеже Монжа, в аксонометрии и стаю кирпичей в перспективе, летящих высоко над горизонтом. Пусть он найдет вторичные проекции. А на каком физическом носителе он будет выполнять задание – не имеет никакого значения. Учащийся должен понять, что прекрасное наглядное изображение на экране компьютера – это не какое-то особое 3D-геометрическое моделирование! Это не особый, исключительный раздел геометрии. Это один из вариантов метода двух изображений. Это аксонометрическая проекция (параллельная или перспективная – по желанию пользователя).

Задание 2. Повышение размерности пространства с R² до R³

Выход в трехмерное пространство как способ решения планиметрических задач и его применение для доказательства теорем рассмотрен в [1]. Большое количество примеров можно найти в задачниках В.А. Пеклича. Предлагается следующее задание.

Пусть плоская кривая задана параметрически:

x=f(t), y=φ(t).                                                                      (1)

Определение ее локальных геометрических характеристик (экстремумов, точек перегиба, радиусов кривизны) затруднительно. Для этого требуется представить ее в явном виде:

y=γ(x).                                                                                    (2)

Как это сделать? Если функции (1) позволяют, можно исключить переменную t. А если функции (1) заданы цифровым массивом?

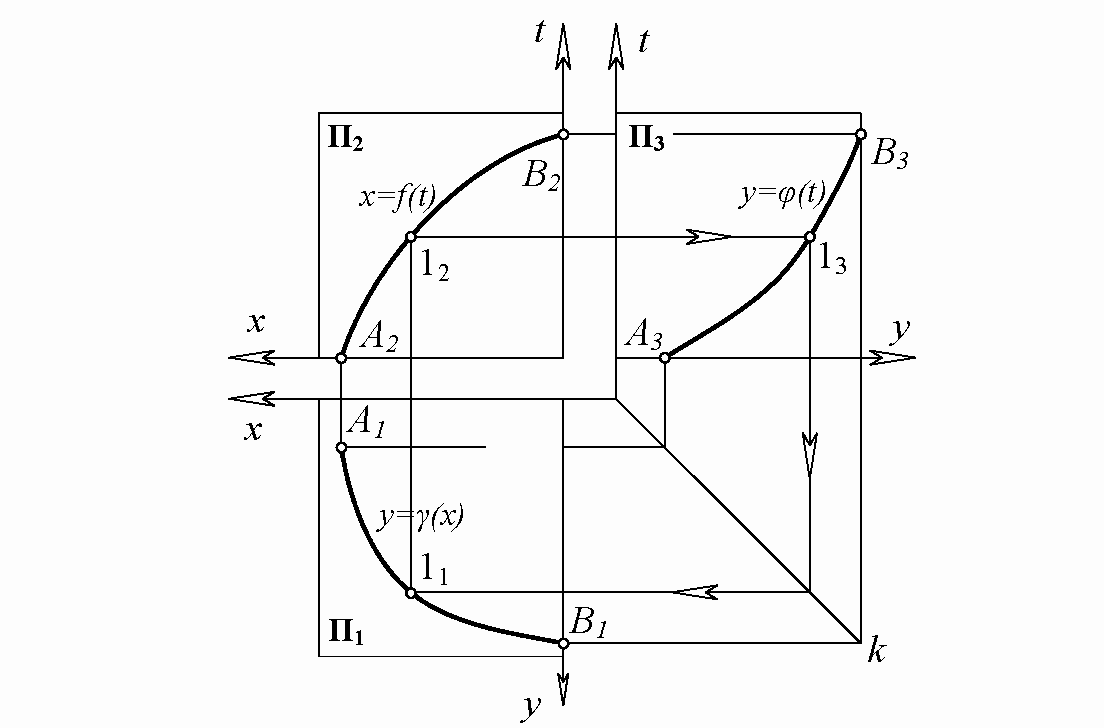
В этом случае задача решается способом повышения размерности объемлющего пространства. Вынесем заданную кривую (1) в трехмерное пространство xyt. Теперь функции (1) описывают не кривую, а ее проекции. Функция x=f(t) – уравнение проекции на плоскость xt. Функция y=φ(t) – уравнение проекции на плоскость yt. Осталось начертить эти проекции, пользуясь уравнениями (1), после чего с помощью постоянной линии чертежа k построить третью проекцию y=γ(x) исследуемой кривой на плоскости xy (рис. 1). Задача решена.

Возникает вопрос – это востребовано? Должно быть, да. Параметризация кривых и поверхностей – основа САПР и компьютерной графики. Вот только сумеет ли будущий компетентный специалист, учивший НГ по слайдам, анимациям и 3D-макетам, решить эту задачу?

Задание 3. Повышение размерности пространства с R³ до R⁴

Рассмотрим ту же задачу, что и в задании 2, но возьмем не плоскую, а параметрически заданную пространственную кривую (пример предложен Г.С. Ивановым):

x=f(t), y=φ(t), z=δ(t).                                                                      (3)

Условие задания сохраняется прежним: надо определить локальные геометрические характеристики заданной пространственной кривой (3). Для этого требуется представить ее в явном виде:

y=γ(x), z=β(x).                                                                                  (4)

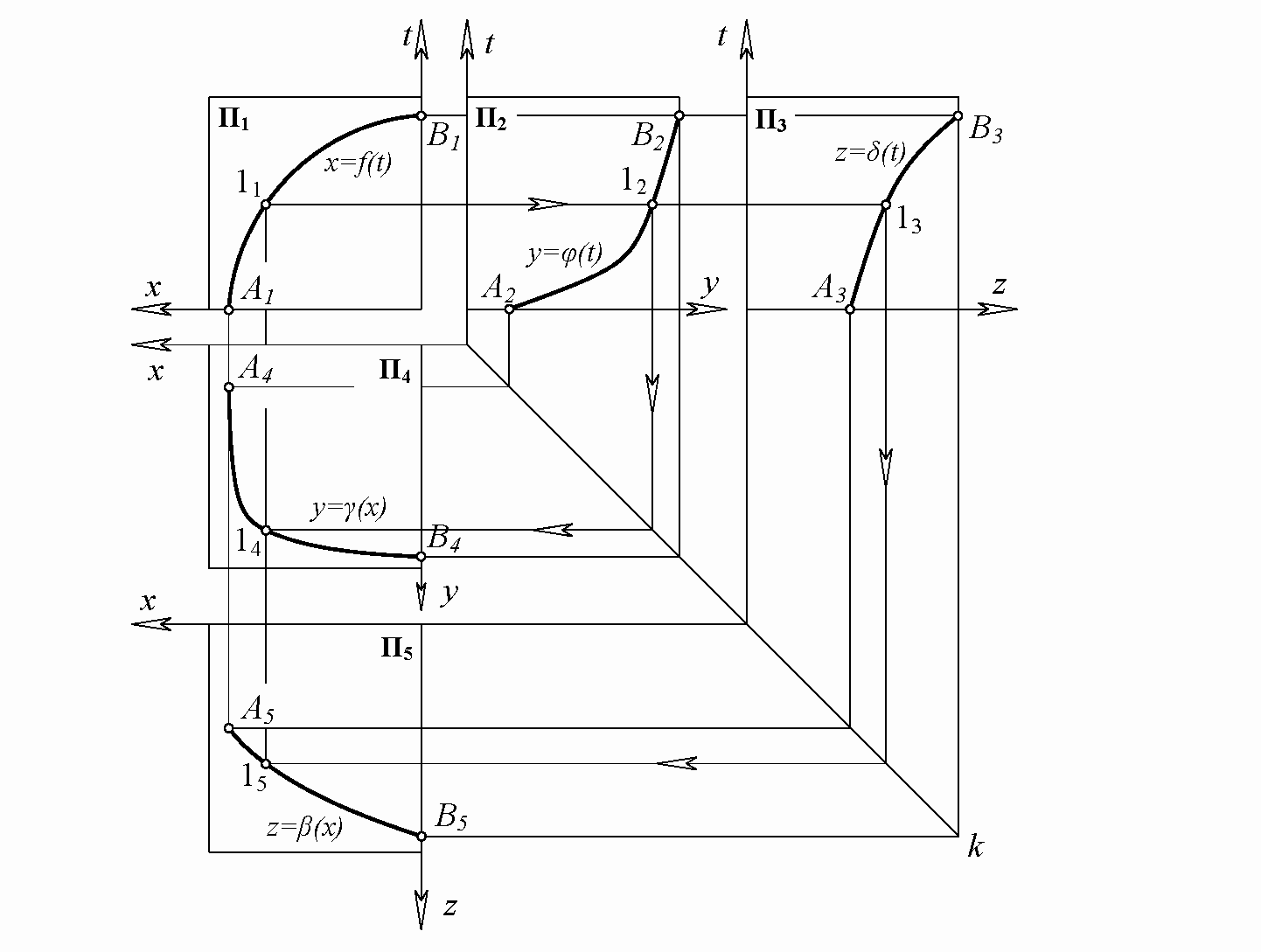
Как и в предыдущем случае, задача решается способом повышения размерности объемлющего пространства. Вынесем заданную кривую в четырехмерное пространство xyzt. Уравнения (3) становятся уравнениями, описывающими не кривую, а ее проекции. На плоскости П₁(xt) имеем проекцию x=f(t), на П₂(yt) имеем y=φ(t), на П₃(zt) – проекцию z=δ(t). Начертив эти кривые, получаем проекционный чертеж (обобщенный чертеж Монжа) пространственной кривой (3), находящейся в четырехмерном пространстве xyzt (рис. 2). Любая точка этой кривой имеет четыре координаты t, x, y, z.

Уравнения (3) представляют собой аналитическую модель нелинейного одномерного пространства, принадлежащего объемлющему четырехмерному пространству. Трехпроекционный чертеж П₁, П₂, П₃ представляет собой графический эквивалент аналитической модели (3). Говорят, что модель (3) и геометрическая модель П₁, П₂, П₃ гомеоморфны.

Не следует беспокоиться, что пространства R⁴ физически не существует. Да, не существует. Но мы можем общаться с этим пространством посредством операции проецирования и тем самым использовать его в своих целях. Комплексных чисел и мнимых точек тоже ведь не существует (в том смысле, что мы не можем на комплексной плоскости отметить их карандашом), но это не мешает нам выполнять с ними алгебраические или графические действия и получать вполне осязаемые результаты.

Таким образом, получен трехпроекционный чертеж пространственной кривой (3), расположенной в R⁴. Дальнейшее решение выполняется так же, как и в задании 2: с помощью постоянной линии чертежа k вычерчиваем проекцию y=γ(x) на плоскости П₄(xy), а также проекцию z=β(x) исследуемой кривой на плоскости П₅(zx) (см. рис. 2). Стрелки на линиях связи помогают понять последовательность построений. Получена модель исследуемой пространственной кривой в форме (4), где функции y=γ(x), z=β(x) зафиксированы не алгебраически, а графически.

В заключение вполне можно предложить студентам сделать на компьютере наглядное аксонометрическое изображение исследуемой кривой. Внимание! Не 3D-макет! Не электронную модель! Эта модель уже есть! После вычерчивания на экране компьютера плоских кривых (3) и (4) эти кривые фиксируются в цифровых двоичных кодах в виде матрицы где-то на жестком диске. Это и есть ЭМИ. Если хочется назвать эту матрицу “3D-моделью исследуемой фигуры”, то вреда от этого никакого не будет. Особого смысла в таком названии нет, но для сокращения речи его можно применять.

Но не называйте 3D-моделью то, что мы видим на экране! На экране не 3D-модель, а ее аксонометрическая проекция! Именно в этом месте начинается путаница и крепчает маразм. То, что эта проекция легко перестраивается и добросовестно позволяет нам менять точку зрения, и фотореалистично раскрашена, не делает обыкновенную аксонометрию новым эксклюзивным геометрическим явлением, ради которого следует отменять или “адаптировать” курс НГ.

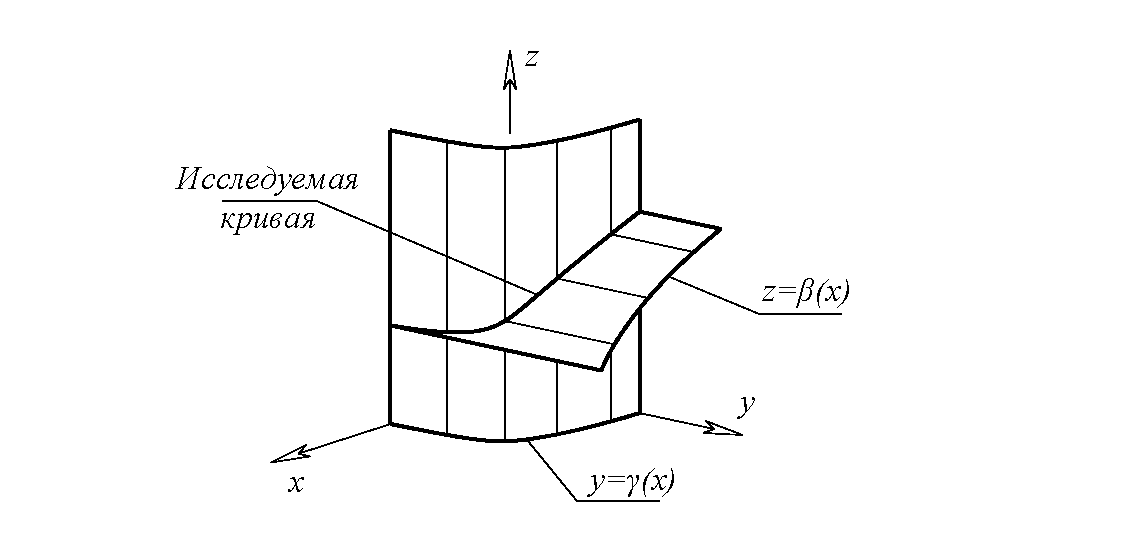
Итак, делаем аксонометрический чертеж исследуемой кривой, представленной в явном виде (4). Уравнение y=γ(x) описывает в декартовых координатах вертикальную цилиндрическую поверхность (образующая параллельна оси z). “Выдавливая” кривую y=γ(x), начерченную в плоскости П₄(xy) (см. рис. 2), в направлении z, получаем цилиндрическую поверхность y=γ(x). На экране немедленно видим ее аксонометрическое изображение. Аналогичным образом, уравнение z=β(x) описывает цилиндрическую поверхность с образующей, параллельной оси y. Выдавливая кривую z=β(x), лежащую в плоскости П₅(xz), в направлении оси y, получаем цилиндрическую поверхность z=β(x). Видим на экране ее аксонометрическую проекцию. Нажимая на кнопку “объединить”, мы инициируем в недрах графического пакета алгебраический (цифровой!) поиск множества точек, инцидентных обеим выдавленным цилиндрическим поверхностям. Получаем на экране аксонометрическое изображение исследуемой кривой (рис. 3). Задача решена.

Заключение. Предлагается ввести в курс начертательной геометрии задание “Пространства различных размерностей”, направленное на изучение основ начертательной геометрии как раздела математики, в котором изучаются методы отображения пространств различных структур и размерностей друг на друга [1]. Учебные часы для выполнения задания можно найти, сократив, например, количество задач на построение линий пересечения фигур.                                                                       

Список литературы

Иванов Г.С. Теоретические основы начертательной геометрии: Учебное пособие / Г.С. Иванов. - М.: Машиностроение, 1998.-157 с.

Рисунки к докладу

К заданию 2. Выход в трехмерное пространство

К заданию 3. Выход в четырехмерное пространство

К заданию 3. Аксонометрическое изображение исследуемой кривой

Кокарева Яна Андреевна (17 марта 2017 г. 13:43)	Здравствуйте, уважаемый Виктор Анатольевич! Прошу прощения, случайно отправилось предыдущее неначатое сообщение... Сама по себе идея о преподавании в вузе таких знаний мне импонирует. Но необходимо всё же учитывать уровень подготовки аудитории. К сожалению, с каждым годом он всё ниже и ниже. Немного смутил Ваш агрессивный напор по поводу 3D. Да, это всего лишь отображение на плоскость экрана, но за этим отображением стоит очень большая работа. И если методами САПР программ всё кажется достаточно просто, то если начинать программирование объекта с графических библиотек (OpenGL, DirectX, WebGL), то приется вспоминать и аффинные преобразования, и перспективу, и еще много чего. Да даже вопрос закрашивания поверхности радужным переходом будет описываться не одной строчкой кода. Как думаете, а такие знания нужны нашим студентам? С уважением, Кокарева Я.А.
Короткий Виктор Анатольевич (17 марта 2017 г. 15:20)	Уважаемая Яна Андреевна, я плоховато понял Ваш вопрос. Какая связь радужного перехода с эпюром Монжа? Извините. С уважением, В. Короткий
Селиверстов Александр Владиславович (17 марта 2017 г. 16:09)	Здравствуйте, Виктор Анатольевич! Читая Ваш доклад, неожиданно понял объяснение "для простого народа", чем отличается геометрия начертательная от аналитической. В первом случае размерность понижается до двух, а во втором - до одного! Ведь координаты точки - это проекции на одномерные оси координат. А дальше понижать некуда. Худшие победят лучшего, как предрекал ещё Дельфийский оракул.
Кокарева Яна Андреевна (17 марта 2017 г. 16:25)	Виктор Анатольевич, в таком разрезе связи никакой. Мой вопрос был вызван недоумением по поводу ярого антагонизма 3D-графике (я про "бесконечное 3D моделирование"). И терминологии. Просто хотела сказать, что внутри заложена большая работа. И геометрические алгоритмы в том числе. Создаются такие программы для уменьшения количества времени на разработку проекта, что повышает эффективность труда. Поэтому немного странно слышать фразы "То, что эта проекция легко перестраивается и добросовестно позволяет нам менять точку зрения, и фотореалистично раскрашена, не делает обыкновенную аксонометрию новым эксклюзивным геометрическим явлением". Мне кажется, разработчики не называют свои программные комплексы "эксклюзивным геометрическим явлением". Это просто инструмент. Не более.
Короткий Виктор Анатольевич (17 марта 2017 г. 17:51)	Яна Андреевна, спасибо Вам за Ваши замечания! С полным почтением отношусь к такой прекрасной штуке, как компьютерная графика! Речь не о ней! Речь о терминах! О терминологических недоразумениях. Рискну предположить, что Вы поняли главное: на экране мы видим аксонометрическое изображение фигуры. На экране мы видим именно аксонометрический чертеж. Можно добавить, что аксонометрия получается посредством обычного аффинного преобразования пространства, но с равным нулю определителем преобразования, чтобы трехмерное отобразить на плоскости. Я не виноват! Никакое это не мифическое 3D! Мы видим плоский проекционный чертеж. Чертеж! Дело в том, что путаница в терминологии дает путаницу в других вещах. Как корабль назвать, так он и поплывет. И еще. Одно ерундовое замечание.Это пустяк, но цитировать надо правильно, а не дергать слова из текста. Вы поставили в цитате точку там, где в тексте была запятая. Это ерунда? Да, запятая - это мелочь. Казнить нельзя помиловать. Ну пожалуйста, дочитайте до конца! Речь о том, что даже самая распрекрасная фотореалистично и радужно раскрашенная аксонометрия не является причиной для отмены или "адаптации" курса НГ. Вы совершенно верно сказали: компьютерная графика есть инструмент! Не более. Так? А инструмент для чего? Для геометрического моделирования, так? Но ведь кажется маленько странным, когда предлагают геометрическое моделирование адаптировать к инструменту для моделирования? Или заменить геометрическое моделирование изучением инструмента для моделирования. Как Вам понравится, если кто-нибудь предложит закон Ома адаптировать к амперметру? Или отменить его изучение, поскольку есть чудесный амперметр. Там такие стрелочки! Зеркальце! Чудо! Сколько труда в него вложено! К черту физику с электротехникой. Они морально устарели. Теперь есть амперметр. Правда, странное предложение? А ведь именно это происходит сегодня в ГГП. Подмена ГГП 3D-моделированием ведет в тупик. Кафедра графики - это общеобразовательный цикл, а не курсы 3D-моделирования. Не обижайтесь, и лучше не ввязывайтесь в эти споры. Это тяжелый разговор. Сосчитайте лучше число окружностей в пространствах R2, R3, R4. Больше пользы будет. Главное Вы поняли - на экране монитора мы видим чертеж. Не забудьте, ладно? Это аксонометрический чертеж фигуры, вся информация о которой содержится в длинных строчках нолей и единиц на жестком диске. Извините за многословие. Не обижайтесь. С уважением, В.А. Держитесь.
Кокарева Яна Андреевна (17 марта 2017 г. 18:26)	Спасибо, Виктор Анатольевич! я знаю. И всегда своим студентам на "Моделировании" рассказываю о том, как формируется изображение на экране. Пошла считать. Держусь )
Сальков Николай Андреевич (18 марта 2017 г. 4:49)	Здравствуйте, Виктор Анатольевич! Замечательное сообщение! Я, правда, тоже хотел было написать об этих "мантрах", даже дошел где-то до 70% текста, но теперь, когда прочитал Ваши "задания", стал сомневаться в нужности своего шага - у Вас очень уж убедительно все расставлено четко по полочкам! Да и ответ Яне Андреевне тоже выдержан в том же стиле! Как говорилось в книжке Булгакова - "я в восхищении!" С уважением, Н. Сальков
Головнин Алексей Алексеевич (18 марта 2017 г. 11:14)	Здравствуйте, Виктор Анатольевич! 1. Не первый год Вы называете экранное изображение ЭМИ аксонометрической проекцией. Вам наверняка известно, что расстояние между точками по аксонометрической проекции не дает представления о действительном расстоянии между точками. На экранном изображении ЭМИ можно измерить расстояния, углы, площади и другие геометрические и массовые характеристики. Несколько лет назад Вы даже привели цитату из Вашего учебного пособия, что аксонометрия – теоретическая основа геометрического моделирования. Была наша просьба сделать доклад на эту тему (понимаем, что это труд и не можем настаивать), но если Вы продолжаете напоминать об этом, то было бы полезным всем, кому интересна эта тема, увидеть хотя бы краткий обзор этого учебного пособия. От себя добавим, что о математическом аппарате геометрического моделирования, на наш взгляд, дает содержание известной книжки Снижко. 2. В заключении Вашего доклада вы пишите «Предлагается ввести в курс начертательной геометрии задание ….». Кому и кем это предлагается? Нет четкости. Если Вы сами себе предлагаете, то вводите, было бы очень интересно увидеть результаты. С уважением Головнин А.А.
Селиверстов Александр Владиславович (18 марта 2017 г. 15:51)	Уважаемый Виктор Анатольевич, Я уже не раз писал на этой конференции о нелепости обязательного преподавания четырёхмерной геометрии на первом курсе (за исключением кружковой работы). Не стану повторять. Но убеждён, что преподавать на первом курсе труднее, чем на старших. Делать это должен только опытный и ответственный Человек. А предложение читать лекции первокурсникам звучит как признание высокой квалификации. Но Ваше замечание "если ректор узнает..." лишь подтверждает, что у Вас "необыкновенная лёгкость в мыслях" (как у Хлестакова). Это же говорит о том, что ректор безусловно достоин уважения.
Сальков Николай Андреевич (18 марта 2017 г. 21:57)	Уважаемый Александр Владиславович, я уже 40 лет работаю с первым курсом, поэтому имею право высказать свое (и не только свое) мнение. Дело в том, что трудности в работе с первокурсниками проистекают в большинстве случаев из-за того, что институт и школа - две большие разницы, и пока студент поймет, как следует учиться в институте, пройдет не менее семестра. Более того, на первый курс принимают, особенно в последнее время, мягко говоря, не всех самых одаренных. И именно с первого курса удаляют всяческих "господ", которые, мягко говоря, не имеют потенции к обучению. После такой отбраковки лишнего материала, на старших курсах, конечно же, преподавателям гораздо проще. Это общепризнанный факт.