МНИМЫЕ ТОЧКИ В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
English version

|
Гирш Антон Георгиевич | (Universität Kassel) |

|
Короткий Виктор Анатольевич | (Южно-уральский государственный университет (Национальный Исследовательский Университет)) |
Аннотация
Рассмотрена геометрическая модель пары комплексно сопряженных мнимых точек на евклидовой плоскости. Геометрическая модель представлена в виде маркера OL. Доказаны теоремы, устанавливающие взаимно однозначное соответствие между действительными координатами маркера и комплексными координатами изображаемых этим маркером пары мнимых сопряженных точек. Предложен графический алгоритм построения окружности, проходящей через действительную точку и через пару мнимых сопряженных точек.
Ключевые слова: Комплексные декартовы координаты, эллиптическая инволюция, изображение мнимых точек.
1. Введение
Основной метод аналитической геометрии заключается в том, что на плоскости или в пространстве вводится система координат, после чего геометрическая задача сводится к составлению и последующему решению системы уравнений.
Если геометрические фигуры описываются алгебраическими уравнениями второй степени и выше, то решение может получаться мнимым. Например, для поиска точек пересечения кубической параболы и прямой линии следует совместно решить алгебраическое уравнение 3 степени общего вида F(x, y)=0 и уравнение прямой Mx+Ny+K=0. Согласно основной теореме алгебры, обязательно получаем три решения (x1, y1), (x2, y2), (x3, y3). Два решения могут выражаться комплексными сопряженными числами. Геометрически это означает, что графики прямой линии и кубической параболы, начерченные в декартовой системе координат X, Y, пересекаются не в трех точках, а только в одной точке.
Если мы намерены в синтетической геометрии следовать за общностью аналитического метода, то нам придется иметь дело с комплексными декартовыми координатами x=a±jb, y=c±jd и придется позволить себе говорить, что комплексные координаты “определяют мнимую точку” [1]. Аналогично придется допустить рассмотрение “мнимых прямых”, то есть прямых линий, описываемых уравнением Mx+Ny+K=0 с комплексными значениями коэффициентов M, N, K.
Возникает естественный вопрос: где находятся мнимые элементы? Ответ кажется очевидным: поскольку мнимые точки есть результат пересечения алгебраических кривых, начерченных на плоскости XY, то мнимые точки находятся на этой плоскости.
С другой стороны, координаты (x, y) мнимых точек выражаются комплексными числами. Множество пар комплексных чисел вида x=a±jb, y=c±jd включает в себя множество пар действительных чисел x=a, y=c. Иными словами, множество действительных точек является лишь частью множества точек с комплексными координатами. Часть не может содержать целое, поэтому множество действительных точек X, Y не может содержать в себе множество мнимых точек.
Получаем противоречие, которое в 19 веке привело к появлению разнообразных геометрических моделей, символически изображающих мнимые точки на вещественной плоскости XY. Модели базируются на том обстоятельстве, что через всякую пару мнимых сопряженных точек A~B с комплексными координатами x=a±jb, y=c±jd проходит единственная действительная прямая m, в чем нетрудно убедиться, подставив координаты заданных мнимых точек в уравнение прямой Mx+Ny+1=0. Мнимые части взаимно сократятся, оставив действительные значения коэффициентов M, N. Действительная прямая m может рассматриваться как фрагмент геометрической модели, указывающей положение пары заданных мнимых сопряженных точек A~B на плоскости XY. Более того, расстояние между мнимыми сопряженными точками выражается комплексным числом (то есть мнимое), но середина этого расстояния является действительной точкой O, инцидентной прямой m. Зная комплексные декартовы координаты точек A~B, нетрудно рассчитать действительные координаты точки O. Точка O, указанная на прямой m, дополняет геометрическую модель мнимых точек A~B.
Разумеется, геометрическая модель {m, O} не позволяет однозначно определить положение мнимых точек A~B на плоскости XY. Модель {m, O} указывает лишь, что эти точки инцидентны прямой m и расположены симметрично относительно точки O. Необходимо дополнить модель {m, O} какой-нибудь геометрической фигурой, однозначно указывающей положение точек A~B на прямой m. Например, можно начертить окружность g2 произвольного радиуса R, проходящую через эти мнимые точки. Для определения коэффициентов u, v уравнения (x-u)2+(y-v)2=R2 окружности достаточно в это уравнение подставить координаты x=a±jb, y=c±jd точек A~B. Перпендикуляр, опущенный из центра G окружности на прямую m, пройдет через точку O. Получаем графический символ, состоящий из прямой линии m и окружности g2, который можно считать геометрической моделью (“графическим образом”) пары сопряженных мнимых точек, заданных комплексными координатами x, y (рис. 1, а). И наоборот, если на плоскости XY “изображена” пара мнимых точек A~B в виде символа “прямая m+окружность g2”, то можно определить комплексные декартовы координаты этих точек, записав и совместно решив уравнения прямой m и окружности g2.
Недостаток предложенной модели заключается в ее информационной избыточности. Действительно, вместо окружности может быть начерчено произвольное коническое сечение, уравнение которого обращается в тождество при подстановке в него координат x=a±jb, y=c±jd изображаемых мнимых точек A~B. Говорят, что такое коническое сечение “проходит” через эти мнимые точки. Через данную пару точек (действительных или мнимых сопряженных) можно провести однопараметрическое множество (пучок) окружностей или двухпараметрическое множество (сеть) конических сечений. Нет никакой необходимости выделять из этого множества некую окружность g2, тем самым придавая ей особое значение.
Этот недостаток модели, представленной на рис. 1, а, нетрудно устранить. Заметим, что все коники, проходящие через мнимые точки A~B, устанавливают на прямой m одну и ту же эллиптическую инволюцию σ(m) сопряженных точек с мнимыми двойными точками A~B. Для однозначного определения этой инволюции достаточно указать всего две пары сопряженных точек. Указав на m произвольную точку M, начертим ее поляру pM в поляритете с ядром g2 (рис. 1, б). Прямая pM пересекает прямую m в точке M'. Получаем пару сопряженных точек M~M'. Точке O соответствует несобственная точка прямой m, поскольку ее поляра в поляритете g2 инцидентна точке O. Точку O называют центром инволюции. Указание на прямой m центра O и пары сопряженных точек M~M' однозначно определяет инволюцию σ(m), установленную на m всеми кониками, проходящими через мнимые точки A~B. Поэтому графический символ “прямая m+окружность g2”, условно изображающий на плоскости XY пару мнимых точек A~B, может быть заменен более простым символом “m + M~M' + O”, не содержащим избыточной информации в виде начерченной окружности.
Графический символ “m + M~M' + O” можно еще более упростить, заметив, что на плоскости XY имеется точка L (ее называют точкой Лагерра), из которой эллиптическая инволюция σ(O, M~M') проецируется ортогональной инволюцией в пучке прямых с центром L. Для построения точки L достаточно провести вспомогательную окружность r2, опирающуюся на отрезок M-M' как на диаметр, и отметить точку L пересечения этой окружности с перпендикуляром, восставленным из центра инволюции O к прямой m (рис. 1, б). Чтобы построить пару точек, сопряженных в инволюции σ(m), надо из точки L провести пару взаимно перпендикулярных лучей до пересечения с m.
Таким образом, точка Лагерра L полностью определяет инволюцию σ(m). Следовательно, для “изображения” на плоскости XY пары мнимых сопряженных точек A~B, заданных своими комплексными координатами x=a±jb, y=c±jd, достаточно начертить действительную прямую m, проходящую через эти мнимые точки, и указать точку Лагерра L. Получаем заметно более простой графический символ “m+OL”, “изображающий” мнимые точки A~B. Следует обратить внимание, что имеется еще одна точка Лагерра L', симметричная точке L относительно m. Из точки L' инволюция σ(m) также проецируется ортогональным пучком прямых (рис. 1, в).
Очевидно, графический символ “m+OL'+OL” можно заменить указанием всего лишь двух точек: точки O (центра инволюции) и точки L (точки Лагерра) (рис. 1, г). Действительно, положение прямой m (носителя инволюции σ) на плоскости XY функционально зависит от положения точек O, L, а именно: прямая m перпендикулярна отрезку OL и инцидентна точке O. Положение второй точки Лагерра L' также вполне определено точками O, L. Получаем лаконичный графический символ {OL}, “изображающий” пару мнимых сопряженных точек на вещественной плоскости XY (см. рис. 1, г). Согласно А.Г. Гиршу, символ {OL} называют маркером мнимых сопряженных точек A~B [3-6].
2. Постановка задачи
Требуется доказать, что на плоскости XY между четырехпараметрическим множеством маркеров OL и четырехпараметрическим множеством пар мнимых сопряженных точек A~B с комплексными координатами x=a±jb, y=c±jd существует взаимно однозначное соответствие, а также указать функциональную взаимосвязь между действительными декартовыми координатами маркера OL и комплексными декартовыми координатами мнимых точек A~B.
Схема решения прямой задачи. Пусть даны мнимые точки A~B с координатами A(x=a+jb, y=c+jd), B(x=a-jb, y=c-jd). Требуется построить маркер OL.
Подставляя координаты заданных мнимых точек в уравнение прямой Mx+Ny+1=0 и в уравнение окружности (x-u)2+(y-v)2=R2 (произвольного радиуса R), находим уравнение действительной прямой m и окружности g2, проходящих через данные мнимые точки A~B. На плоскости XY начертим прямую m и окружность g2. Получаем графический символ {m, g2}, “изображающий” точки A~B с заданными мнимыми координатами x, y (см. рис. 1, а). Перпендикуляр, опущенный из центра G окружности g2 на прямую m, указывает центр O эллиптической инволюции σ(m), установленной на m окружностью g2. Отметив на m произвольную точку M, находим ее поляру pM. На пересечении этой поляры с прямой m отмечаем точку M', сопряженную с M в инволюции σ(m). Начертив вспомогательную окружность r2, отмечаем точку Лагерра L (см. рис. 1, б). Маркер OL построен.
Схема решения обратной задачи. На плоскости XY начерчен маркер OL, символически изображающий пару мнимых сопряженных точек A~B (см. рис. 1, г). Требуется определить декартовы координаты A(x=a+jb, y=c+jd), B(x=a-jb, y=c-jd) мнимых точек A~B.
Начертим прямую m, проходящую через точку O перпендикулярно отрезку OL. Точка Лагерра L однозначно определяет эллиптическую инволюцию σ на прямой m. Начертим какую-нибудь конику (например, окружность g2), устанавливающую на прямой m инволюцию σ. Запишем и совместно решим уравнения прямой m и коники g2. Получаем два решения, которые и являются искомыми декартовыми координатами мнимых точек A~B, заданных маркером OL.
Исследование. Предложенные графоаналитические схемы решения прямой и обратной задач не могут считаться удовлетворительными в силу их чрезмерной конструктивной сложности и сомнительной точности. Кроме того, в схеме решения обратной задачи не рассмотрен вопрос построения окружности, устанавливающей на прямой m инволюцию σ. Ответ на этот вопрос дает следующая теорема.
Теорема 1. Если эллиптическая инволюция σ на прямой m задана центром инволюции O и точкой Лагерра L, то любая окружность g2 с центром G на прямой n=OL, ортогональная к окружности r2(O, OL), устанавливает на прямой m инволюцию σ.
Доказательство теоремы основано на следующей лемме (О.А. Вольберг): две проекции точки T конического сечения g2 из концов какой-либо его хорды D-D' на прямую m, сопряженную с этой хордой в поляритете с ядром g2, являются соответственными в инволюции σ, установленной коникой g2 на прямой m [2, стр. 140].
Начертим произвольное коническое сечение, например, окружность g2, и произвольную прямую m, не пересекающуюся с g2. Из центра O окружности опустим перпендикуляр n на прямую m. Отметим точки D, D' пересечения прямой n и окружности g2. Отметим на g2 произвольную точку T (рис. 2, а). Прямая n=DD' сопряжена с m в поляритете g2, так как в этом поляритете прямая n является полярой несобственной точки прямой m. Проецируем точку T из концов диаметра DD' на прямую m. Получаем точки M, M'. Согласно лемме, эти точки сопряжены в инволюции σ, установленной окружностью g2 на прямой m.
Возвращаясь к доказываемой теореме, начертим окружность r2(O, OL) и отметим точки пересечения M, M' прямой m с окружностью r2 (рис. 2, б). Укажем на окружности r2 произвольную точку T и построим проекции D, D' точек M, M' из точки T на прямую n=OL. На отрезке DD' как на диаметре построим окружность g2. Согласно лемме О.А. Вольберга, окружность g2 устанавливает на m инволюцию γ, в которой точки M и M' являются соответственными. Но точки M, M' сопряжены также и в инволюции σ, которая установлена на прямой m точкой Лагерра L. Кроме того, точка O является как центром инволюции γ, так и центром инволюции σ, следовательно, инволюции γ и σ тождественны. Иначе говоря, построенная нами окружность g2 устанавливает на m инволюцию σ, заданную в условии теоремы центром O и точкой Лагерра L.
Покажем, что окружность g2 ортогональна окружности r2. Соответственные стороны подобных прямоугольных треугольников MTM' и DTD' взаимно перпендикулярны, следовательно, их медианы OT и GT также взаимно перпендикулярны. Но OT и GT – радиусы окружностей r2 и g2, следовательно, эти окружности ортогональны (пересекаются под прямым углом). Таким образом, произвольная окружность g2 с центром на прямой n=OL, ортогонально пересекающаяся с окружностью r2(O, OL), устанавливает на прямой m ту же самую инволюцию σ, что установлена на прямой m точкой Лагерра L. Теорема 1 доказана.
Следствие из теоремы 1. Множество окружностей с центрами на прямой n=OL, ортогонально пересекающиеся с окружностью r2(O, OL), образуют пучок с мнимыми базисными точками A~B, заданными маркером OL (рис. 2, в). Особо отметим, что в этом пучке имеются две окружности нулевого радиуса r0 и r0' с центрами в точках L и L'. Как и все окружности пучка, нулевые окружности также инцидентны мнимым точкам A~B.
На основании теоремы 1 и следствия из нее доказывается теорема 2, устанавливающая взаимосвязь действительных декартовых координат точек O, L, входящих в состав маркера OL, и комплексных декартовых координат мнимых точек A~B, “изображаемых” на плоскости XY маркером OL.
3. Взаимно однозначное соответствие между координатами мнимых
сопряженных точек и координатами маркера, изображающего эти точки
Взаимно однозначное соответствие между координатами мнимых сопряженных точек A(x=a+jb, y=c+jd)~B(x=a-jb, y=c-jd) и координатами точек O, L маркера OL, изображающего эти точки, определено следующей теоремой.
Теорема 2. Если на декартовой плоскости XY задан маркер OL, символически изображающий пару мнимых сопряженных точек A~B, то между действительными координатами точек O(x0, y0), L(xL, yL) и комплексными координатами A(x=a+jb, y=c+jd), B(x=a-jb, y=c-jd) мнимых точек A~B установлено следующее взаимно однозначное соответствие: a=x0, b=y0-yL, c=y0, d=xL-x0, где в качестве координат xL, yL могут быть указаны как координаты точки L, так и координаты точки L' (точки Лагерра L и L' расположены симметрично относительно прямой m=AB).
Доказательство. Уравнение прямой m, проходящей через O перпендикулярно к OL, имеет вид
y=y0-(x-x0)(xL-x0)/(yL-y0) (1)
Числовые значения коэффициентов этого уравнения не меняются при подстановке в него координат точки L' вместо координат точки L.
Предположим, что теорема верна, то есть a=x0, b=y0-yL, c=y0, d=xL-x0. В этом случае уравнение (1) прямой m приобретает вид
y=c+d(x-a)/b (1')
Уравнение окружности r0 нулевого радиуса с центром в точке L:
(x-xL)2+(y-yL)2=0 (2)
Согласно доказываемому утверждению имеем: xL=d+a, yL=c-b. Подставляя эти выражения в (2), получаем:
(x-d-a)2+(y-c+b)2=0 (2')
Напомним, что, согласно следствию из теоремы 1, окружность r0 пересекается с прямой m в мнимых сопряженных точках A~B, изображенных на плоскости XY маркером OL. Следовательно, чтобы найти декартовы координаты этих мнимых точек надо совместно решить уравнения (1') и (2') прямой m и нулевой окружности r0. Подставляя выражение (1') в уравнение (2'), после простых алгебраических преобразований получаем квадратное уравнение относительно координаты x точек A~B:
x2-2ax +a2+b2=0 (3)
Решая уравнение (3), получаем: x=a±jb. Подставляя полученные значения x в уравнение (1'), получаем: y=c±jd. Результат соответствует условию теоремы, следовательно, теорема 2 верна.
Подстановка в уравнение (2) координат точки L' вместо координат точки L приводит к тому, что мнимые сопряженные точки A~B “меняются местами”. Пусть, например, на плоскости XY указан маркер OL с координатами O(x0=2, y0=4), L(xL=3, yL=2), L'(xL'=1, yL'=6), “изображающий” пару мнимых сопряженных точек A~B. Обращаясь к теореме 2, получаем координаты точки A: xA=2+2j, yA=4+j. Координаты сопряженной с A точки B равны: xB=2-2j, yB=4-j. Если же вместо координат точки L использовать координаты точки L'(1, 6), то, согласно теореме 2, координаты точки A равны xA=2-2j, yA=4-j, а координаты сопряженной точки B равны xB=2+2j, yB=4+j, то есть сопряженные точки A~B “поменялись местами”.
4. Мнимые точки в начертательной геометрии
Мнимые точки в конструктивных задачах начертательной геометрии появляются при операциях с алгебраическими линиями и поверхностями, определяя или задавая условия инцидентности, которым должна удовлетворять искомая фигура.
Пример. На плоскости XY построить окружность, проходящую через действительную точку C(xC, yC) и через пару мнимых сопряженных точек A~B с координатами x=a±jb, y=c+jd.
Алгебраическое решение задачи: в уравнение окружности (x-u)2+(y-v)2=R2 подставляем декартовы координаты точек A, B, C, после чего из полученной системы уравнений находим значения коэффициентов u,v, R уравнения окружности.
Рассмотрим геометрический эквивалент алгебраического решения. Предварительно перейдем к графическому представлению мнимых точек A~B в виде маркера OL. Координаты точек O, L на плоскости XY определяются в соответствии с теоремой 2: x0=a, y0=c, xL=d+a, yL=c-b. Получаем геометрическую формулировку задачи: построить конику (окружность) g2, заданную пятью точками: действительной точкой C, циклическими точками I, J и двумя мнимыми сопряженными точками A~B, изображаемыми маркером OL (рис. 3, слева) [7].
Начертим прямую m, проходящую через точку O перпендикулярно к прямой n=OL (рис. 3, справа). Искомая окружность g2 устанавливает на прямой m эллиптическую инволюцию σ с центром O, а на несобственной прямой – абсолютную инволюцию α. В поляритете g2 прямая n=OL сопряжена как с несобственной прямой, так и с прямой m. Пусть прямая n пересекает искомую окружность g2 в точках F, H. Для полного решения поставленной задачи достаточно найти эти точки. При этом окружность g2 будет вполне определена точками C, F, H.
Алгоритм построения точек F, H основан на лемме О.А. Вольберга, использованной при доказательстве теоремы 1: проекция инволюции на прямой m из произвольной точки C, инцидентной g2, на прямую n, сопряженную с m в поляритете g2, есть инволюция, преобразующая точки F, H друг в друга.
В рассматриваемой задаче надо на прямую n, сопряженную с m, спроецировать из точки C две инволюции: инволюцию σ(m) и абсолютную инволюцию α(I, J). Общая пара этих инволюций указывает искомые точки F, H.
Действие 1. Используя маркер OM, отмечаем на прямой m две произвольные пары точек 1~1', 2~2', соответственные в инволюции σ, установленной искомой окружностью g2 на прямой m.
Действие 2. Проецируем точки 1~1', 2~2' из точки C на произвольную окружность e2, проходящую через C. Получаем на e2 инволюцию 1e~1e', 2e~2e' с центром S. Абсолютная инволюция α проецируется из точки C ортогональным пучком прямых, который высекает на e2 инволюцию с центром, совпадающим с центром E окружности e2. Прямая ES пересекается с e2 в точках Fe, He, указывающих общую пару инволюций на вспомогательной окружности e2.
Действие 3. Точки Fe, He проецируем из точки C на прямую n. Получаем на прямой n точки F, H, через которые проходит искомая окружность g2(C, F, H) (см. рис. 3, справа).
Проверка. Если построение выполнено верно, то центр G найденной окружности инцидентен прямой n.
5. Заключение
Теорема 2 устанавливает взаимно однозначное соответствие между комплекснозначными декартовыми координатами A(x=a+jb, y=c+jd), B(x=a-jb, y=c-jd) мнимых сопряженных точек A~B и действительными координатами точек O(x0, y0), L(xL, yL) маркера {OL}, символически изображающего мнимые точки A~B на плоскости XY: x0=a, y0=c, xL=d+a, yL=c-b.
Доказанное в теореме 2 соответствие x0=a, y0=c, xL=d+a, yL=c-b позволяет исключительно просто переходить от аналитического (координатного) указания мнимых точек к их графическому изображению в виде предложенного А.Г. Гиршем маркера {OL}, и наоборот – по графическому изображению пары сопряженных мнимых точек в виде маркера {OL} определять комплексные декартовы координаты этих точек.
Список литературы
1. Бюшгенс, С.С. Аналитическая геометрия. Первый концентр, вып. 1/ С.С. Бюшгенс. – М.-Л.: Объединенное научно-техническое изд-во НКТП СССР. Государственное технико-теоретическое изд-во, 1934. – 237 с.
2. Вольберг, О. А. Основные идеи проективной геометрии / О. А. Вольберг. – М.-Л.: Учпедгиз, 1949. – 188 с.
3. Гирш А.Г. Наглядная мнимая геометрия. – М.: ООО «ИПЦ "Маска"», 2008. – 216 с.
4. Гирш А.Г. Комплексная геометрия – евклидова и псевдоевклидова. – М.: ООО «ИПЦ "Маска"», 2013. – 216 с.
5. Гирш А.Г. Начала комплексной геометрии. Сборник задач по комплексной геометрии с решениями. Часть I ─ 2D. Кассель, 2012. ─ 191 с.
6. Гирш А.Г. Начала комплексной геометрии. Избранные задачи комплексной геометрии с решениями. Часть II ─ 3D. Кассель, 2014. ─ 112 с.
7. Гирш А.Г., Короткий В. А. Графические алгоритмы реконструкции кривой второго порядка, заданной мнимыми элементами. // Геометрия и графика. 2016. Т. 4. №. 4. C. 19-30. DOI: 10.12737/22840
Рисунки к докладу
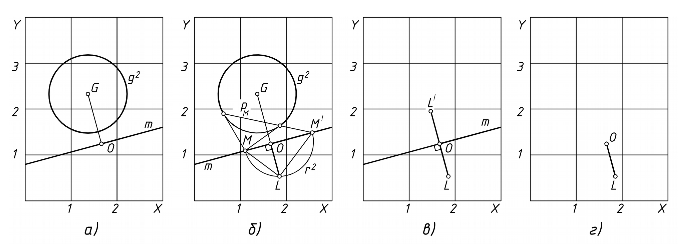
Рис. 1 Изображение мнимых точек на действительной плоскости XY: а) графический символ “окружность+прямая”; б) эллиптическая инволюция и точка Лагерра; в) маркер с двумя точками Лагерра; г) маркер {OL}
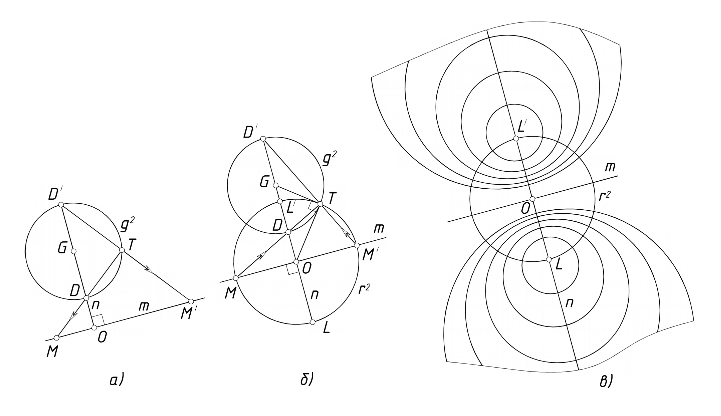
Рис. 2 К доказательству теоремы 1: а) построение сопряженных точек на прямой m в поляритете g2; б) построение окружности g2, инцидентной мнимым точкам, заданным маркером OL; в) пучок окружностей, ортогональных к r2
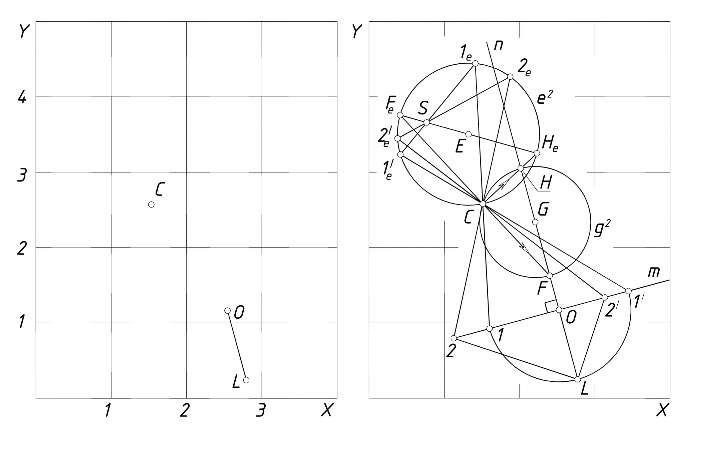
Рис. 3 Построение окружности, проходящей через действительную и две мнимые точки: условие задачи (слева); решение (справа)
Вопросы и комментарии к выступлению:

Селиверстов Александр Владиславович (28 февраля 2019 г. 2:34) |
Уважаемые Антон Георгиевич и Виктор Анатольевич! |

Гирш Антон Георгиевич (28 февраля 2019 г. 15:07) |
Уважаемый Александр Владиславович, спасибо, что заглянули в эту статью, менее приятно примечание про "человеческую глупость". Тема то относительно новая в прикладной геометрии, термины ещё не обкатаны и не общеприняты, так что шероховатосей быть не должны, но возможны. Будем работать над ошибками. |

Короткий Виктор Анатольевич (28 февраля 2019 г. 17:45) |
Уважаемые коллеги, в статье содержится грубая ошибка: множество коник, проходящих через две наперед заданные точки на плоскости, является трехпараметрическим множеством, а совсем не сетью (двухпараметрическим множеством), как неверно указано в статье. С уважением, авторы |

Селиверстов Александр Владиславович (1 марта 2019 г. 13:10) |
Здравствуйте, Антон Георгиевич! |

Гирш Антон Георгиевич (2 марта 2019 г. 17:16) |
Радиус окружности +R или -R всего лишь означает, что радиус отложен от центра вправо или влево. Но если Вы хотите получить мнимую окружность, то радиус должен нести сомножитель i, т.е. корень из -1. О Пекличе молчу, он вошёл в чужую тему и очень торопился. |
Назад Go Back
