ИЗОЛИРОВАННЫЕ ЭЛЕМЕНТЫ ПОВЕРХНОСТЕЙ
English version

|
Гирш Антон Георгиевич | (Universität Kassel) |
Аннотация
Алгебраическая кривая порядка п может содержать не больше, чем (п-1)(п-2)/2 двойных точек, если точек больше - кривая распадается. Но известны случаи, когда кривая распадается и при меньшем числе двойных точек. Анализу таких случаев и посвящена статья. Анализ показал наличие и природу "недостающих" для распадения двойных точек распадающихся кривых. Число двойных точек, необходимых для распадения кривой, во всех случаях соответствует формуле, но "недостающие" точки по своей природе оказываются мнимыми изолированными.
Ключевые слова: асимптота; двойные точки; коника; кривая; меридиан; ось вращения; изолированные точки; изолированная коника; поверхность; касательная плоскость; сечение; распадение.
Введение
Евклидова геометрия является строго построенной дедуктивной системой. Она лежит в основе начертательной геометрии, конструктивной геометрии и, что сегодня актуально, в основе компьютерной геометрии. А между тем в практике геометрических конструкций обнаруживаются изъяны. Так, теорема Гаусса утверждает, что две кривые порядков m и n имеют ровно mn точек пересечения. Окружность есть кривая второго порядка. Две окружности должны иметь четыре точки пересечения. Но точек пересечения окружностей может вовсе не быть и, если постараться, их может быть самое большее две. Этот простой пример указывает на то, что система евклидовой геометрии требует более пристального внимания и нуждается в некоторых разъяснениях.
Особенности дополненной евклидовой геометрии
- Евклидова геометрия строго построенная, но незамкнутая система. Это значит, что в результате геометрических операций над геометрическими фигурами, может появиться фигура, которой не содержится в евклидовой геометрии, чуждая её природе. Евклидово пространство - только часть комплексного пространства, состоящего, подобно комплексным числам, из действительных и мнимых фигур. Евклидова геометрия оперирует только действительными фигурами. Мнимые фигуры чужды ей и принадлежат некоей другой геометрии. Сложилась такая практика, что если решение выводит на мнимый результат, то оно либо отбрасывается, либо меняются условия задачи. Примером замкнутой системы служит аналитическая геометрия, оперирующая комплексными числами. Аналитическая операция может дать в результате действительное число, мнимое или комплексное. Первые два суть составные части третьего.
- Евклидова геометрия нуждается в комплексном расширении. В евклидовой геометрии необходимо допустить существование комплексных фигур, в которых действительные фигуры были бы ведущими, но дополненными мнимыми составляющими.
- В евклидовой геометрии следует различать два принципиально различных класса фигур. 1) Аналитические фигуры, они имеют аналитическую поддержку и являются графиками аналитических формул и 2) Синтетические фигуры, они не имеют аналитической поддержки. Эллипс является аналитической фигурой и имеет с прямой линией всегда две точки пересечения, действительные, совпавшие или мнимые, овал синтетическая фигура, имеет с прямой линией две, одну или ни одной точки пересечения. Мнимых точек синтетическая фигура иметь не может.
- Каждая действительная фигура окружена множеством сопряжённых с ней мнимых дополнений. Конкретное мнимое дополнение выделяется из множества данной геометрической операцией. Операция определяет вектор мнимого направления.
- Если две действительные фигуры не имеют действительного пересечения, то они имеют мнимое пересечение.
- Для возможности в геометрических конструкциях оперировать мнимыми фигурами (поскольку они часть геометрии, но невидимы для «евклидового глаза») их необходимо сделать видимыми и показывать, например, особым типом линии; такой линией здесь принята штриховая.
- Пополненная таким образом евклидова геометрия уже не будет давать сбои в построениях и все теоремы, включая теорему Гаусса, будут беспрекословно и с очевидностью исполняться. Визуализация мнимых дополнений кривых второго порядка не потребует расширения размерности пространства, что будет показано на приводимых ниже примерах [1, 2, 3].
Распадение алгебраической кривой
Для дальнейшего нам будет нужна теорема Маклорена (MacLaurin) о двойных точках алгебраической кривой n-го порядка: «Нераспадающаяся кривая n-го порядка может иметь до dn=(n -1)(n -2)/2 двойных точек». Кривая второго порядка двойных точек не имеет, кривая третьего порядка может иметь одну двойную точку, кривая четвёртого порядка может иметь до трёх двойных точек. Имей эти кривые одной двойной точкой больше, они распались бы на составляющие более низкого порядка. Так, кривая второго порядка может распасться на две прямые, кривая четвёртого порядка может распасться на две коники или на прямую и кубику [4, 5].
Анализ поверхностей вращения
Пример 1. Открытый круговой тор имеет меридиан, состоящий из двух окружностей, симметричных относительно оси а, рис. 1. Меридианные окружности m1 и m2 должны иметь четыре точки пересечения. Покажем их. Окружности m1 и m2 как аналитические кривые имеют своими мнимыми дополнениями равнобочные гиперболы, мнимые оси которых направлены по оси а меридиана. Гиперболы пересекаются на оси а в двух мнимых двойных точках Р1 и Р2. Гиперболы далее пересекаются ещё в двух мнимых двойных точках Q1 и Q2 (ветви h и h' указывают на положение точки Q2). Точки Q1 и Q2 несобственные, известны как циклические, через которые проходят все окружности плоскости. Теорема Гаусса удовлетворена. «Если две кривые не имеют действительных точек пересечения, то они имеют мнимые точки пересечения».
Переходя от меридиана к поверхности тора Ψ(а, m12), обратим внимание, что обычный открытый тор пополнился двумя изолированными точками Р1 и Р2 и несобственной изолированной сферической окружностью q, полученной от вращения циклических точек Q1 и Q2 вокруг оси а. Определим координаты точек Р1 и Р2. Пусть образующая окружность тора имеет уравнение (x2-d)2 +x32 = r2, сечение окружности прямой x3=±√(r2 - d2) определяет на оси а точки Р12 с координатой x2=0 как нулевую параллель и ещё одну мнимую параллель тора с радиусом x2=2d [5, 6].
Далее, рассмотрим плоское сечение тора как кривую четвёртого порядка и условия его распадения по теореме Маклорена. Для распадения кривой сечения необходимо в секущей плоскости иметь четыре двойные точки. Две точки находятся легко как точки прикасания к тору внутренней дважды касательной плоскости τ. Это точки R1 и R2. Дальнейшими двумя двойными точками будут точки М1 и М2 пересечения плоскости τ с несобственной двойной окружностью q. На какие кривые распадётся квадрика сечения? На две конгруэнтные коники, потому что прямая R1R2 есть ось симметрии квадрики. Коники будут окружностями, потому что проходят через циклические точки. Этим доказана теорема Вилларсо (Y.Villarceau, 1848): «Каждая плоскость двойного касания τ кругового тора Ψ рассекает его по двум конгруэнтным окружностям».
Пример 2. Меридиан поверхности вращения состоит из двух эллипсов общего положения, не пересекающих ось симметрии.
Если эллипсы будут в осепараллельном положении, то они повторят свойства окружностей по примеру 1 с парой несобственных мнимых точек. Для эллипсов, наклонённых к оси симметрии а, все точки пересечения собственные, Р1, Р2 лежат на оси а, точки Q1, Q2 лежат симметрично оси а. В этих точках пересекаются мнимые дополнения эллипсов в форме сопряжённых гипербол h1 и h2. Из множества гипербол, окружающих эллипсы, в пересечение вступают те, мнимые оси которых параллельны их радикальной оси а. Мнимые гиперболы базируются на сопряжённых диаметрах несущих эллипсов сопряжённые диаметры показаны знаком параллельности.
Торовая поверхность Ψ(а, m12) имеет действительную внутреннюю дважды касательную плоскость τ, которая несёт четыре двойные точки - действительные двойные точки касания R1, R2 и пару мнимых двойных точек М1 и М2 как точки пересечения плоскости τ с окружностью q(Q1, Q2). Условие распадения кривой сечения в плоскости τ удовлетворено. Форма кривой сечения определяется следующими двумя предложениями [7]:
«Коники τ-сечения подобны коникам m-сечения и подобно расположены».
«Если коники m-сечения принадлежат гиперболическому пучку (с мнимыми двойными точками на радикальной оси), то коники τ-сечения принадлежат эллиптическому пучку (с действительными двойными точками на радикальной оси) и наоборот», см. рис. 1.
Пример 3. Меридиан поверхности вращения состоит из двух пересекающихся окружностей m1, m2, пересекающихся на оси а в действительных точках Р1, Р2, рис. 2. Пересекающиеся окружности не имеют действительных внутренних касательных, но их мнимые дополнения в форме равнобочных гипербол имеют внутренние касательные. Здесь построение уходит в область мнимого, а это уже не евклидова, а псевдоевклидова геометрия [8, 9].
Касательная прямая τ из внутренней точки О окружности m1 проходит через точку В1 пересечения её с полярой b1 точки О относительно окружности m1. Мнимый отрезок ОВ1 как наклонённый к оси координат представлен с искажением. Его истинная величина определится на оси координат в гиперболическом повороте отрезка ОВ1, рис. 2с, и будет равна длине отрезка ОР1. Поворотом вокруг точки О точка Р1 совмещается с точкой Вh. Истинная длина отрезка ОВ1 равна длине отрезка ОВh. В результате определены четыре двойные точки в плоскости сечения закрытого тора плоскостью τ - это пара точек Вh и пара точек в пересечении несобственной сферической окружности плоскостью τ. Кривая сечения с необходимостью распадается на две конгруэнтные кривые, рис. 2b. Отрезок оси х2 фигуры меридиана равен по длине отрезку оси х1 фигуры сечения, рис. 2a, b.
Пример 4. Образующая кривая поверхности Ψ вращения есть парабола m1 в осепараллельном положении. Меридиан m12 поверхности Ψ имеет на оси вращения а две изолированные мнимые двойные точки Р1, Р2, рис. 3а. В этих точках пересекаются мнимые дополнения парабол m1, m2 с мнимым вектором по оси а, нормально к осям парабол. Поэтому оси дополняющих парабол совпадают с осями парабол-носителей и имеют тот же параметр. Ещё две точки Q1, Q2 пересечения парабол m1, m2 меридиана будут несобственными совпавшими дважды двойными мнимыми точками на оси х2.
Дважды касательная плоскость τ пересекает поверхность Ψ по кривой четвёртого порядка, которая имеет четыре двойные точки - действительные точки касания R1, R2 и дважды двойная мнимая точка Q12 на оси х2. Кривая сечения распадается на две конгруэнтные кривые с совпадающими на оси х2 осями, пересекающимися в точках R1, R2. Наличие у кривой несобственной дважды двойной точки Q12 определяет кривые как параболы. На рис. 3b в осях Ох1х3 показана проекция кривой сечения поверхности Ψ дважды касательной плоскостью τ.
Пример 5. Образующая кривая поверхности Ψ вращения есть гипербола m1 с асимптотами, наклонёнными к действительной оси гиперболы под углом 30°. Гипербола повёрнута так, что её асимптота совпадает с координатной осью Ох2, рис. 4а. Поверхности вращения Ψ для лучшего восприятия мы назвали «шляпы». У меридиана m12 с осью х2 совпадают сразу две асимптоты. Ось вращения поверхности Ψ есть прямая а и с ней совпадает мнимый вектор i. Гиперболы меридиана в плоскости Ох2х3 дополняются сопряжёнными с ними эллипсами так, что касательные в точках касания параллельны оси а. Два мнимых эллипса пересекаются в двух парах мнимых двойных изолированных точках - в точках Р1, Р2 на оси а и в точках Q1, Q2 на оси Ох2. При вращении вокруг оси а точки Q1, Q2 заметают двойную изолированную окружность q.
1. Плоскость двойного касания τ проходит параллельно оси а и касается поверхности Ψ в действительных двойных точках R1, R2 и пересекает изолированную окружность q в мнимых двойных точках М1, М2. Итак, кривая четвёртого порядка от сечения поверхности Ψ дважды касательной плоскостью τ имеет четыре двойные точки и с необходимостью распадается на две кривые второго порядка - на две гиперболы, рис. 4а, b. Одна асимптота гипербол совпадает с осью Ох1, вторая наклонена к оси гиперболы под углом 60°. Гиперболы пересекаются в точках R1, R2 [9, 10].
2. Поверхность «шляпы» позволяет дальнейшую секущую плоскость двойного касания - плоскость τ2, проходящую через асимптоту t. Плоскость τ2 коснется поверхности Ψ в дважды двойной несобственной точке гиперболы m1, рис. 4а, и пересечёт изолированную окружность q в двойных мнимых точках М1, М2. Условие распадения кривой удовлетворено. Сечение имеет форму кривой «прямой крест», состоящий из двух гипербол в чётных и нечётных квадрантах, имеющих своими асимптотами координатные оси Ох1 и Ох4, совпадающей с асимптотой t.
3. Третья секущая плоскость τ3, ведущая к распадению кривой сечения поверхности «шляпы», есть координатная плоскость Ох1х2. Плоскость, лежащая между полями шляп, не имеет реального пересечения с поверхностью, но имеет сечение в комплексном расширении действительных фигур. Кривая четвёртого порядка, каким и должно быть плоское сечение поверхности четвёртого порядка, распадается на две окружности - на окружность q и несобственную сферическую окружность от вращающихся вокруг оси а асимптотических точек множества гипербол.
Заключение
Если теорема Гаусса утверждает, что две кривые порядков m и п имеют ровно mп точек пересечения, то в это число входят и мнимые точки. Так два эллипса имеют четыре точки пересечения, которые все могут быть мнимыми. В мнимых точках пересекаются не сами действительные эллипсы, а их мнимые дополнения, которые сопряжены с данными действительными эллипсами. Мнимые образы как комплексные расширения действительных фигур в наших примерах показали, что на оси вращения поверхности всегда имеется пара двойных точек пересечения коник меридиана. Если коники меридиана не пересекают ось вращения, то двойные точки на оси будут мнимыми изолированными. Кроме двойных мнимых точек на оси меридиана коники будут иметь и вторую пару мнимых двойных точек, лежащих симметрично оси. Эта пара точек при переходе к поверхности вращения образуют двойную изолированную мнимую окружность. Эта окружность играла в наших примерах важную роль. Она доставляла пару двойных точек пересечения её с секущей плоскостью, дополняющих две двойные точки касания секущей плоскости с поверхностью вращения до четырёх двойных точек, необходимых для распадения кривой сечения, имеющей четвёртый порядок. Кривая сечения распадалась на две коник, симметричных относительно прямой через точки касания.
Приведённые примеры с вовлечением мнимых образов в действительные конструкции показали их несомненную пользу в понимании сути геометрической операции. Решения задач евклидовой геометрии при особом сочетании исходных условий могут вести в область мнимых значений. Евклидова геометрия решает геометрические задачи, но не рассматривает фигуры решения, попавшие в область мнимого. Они для неё невидимые. Задача геометра такие случаи отслеживать и создавать для мнимых геометрических образов мысленные и графические формы. В этой статье успешно применён опыт изображения мнимых образов первого и второго порядков штриховыми линиями без дополнения 3D-пространства новыми измерениями.
Список литературы
- Щербаков Р.Н., Пичурин Л.Ф. От проективной геометрии – к неевклидовой (вокруг абсолюта). – М.: Просвещение, -- 1979. – 160 с.
- Гирш А.Г. Наглядная мнимая геометрия. – М.: ООО «ИПЦ "Маска"», 2008. – 216 с.
- Гирш А.Г. Комплексная геометрия – евклидова и псевдоевклидова. – М.: ООО «ИПЦ "Маска"», 2013. – 216 с.
- Glaeser, G. Geometrie und ihre Anwendungen in Kunst, Natur und Technik. Wien: SpringerSpektrum, 2014. 508 S.
- Иванов Г.С., Дмитриева И.М. О задачах начертательной геометрии с мнимыми решениями. // Геометрия и графика. 2015, Т.3, №2. С. 3-8. DOI: 10.12737/12163.
- Гирш А. Г. Мнимости в геометрии. // Геометрия и графика. 2014. Т 2. №. 2. C. 3-8. DOI: 10.12737/5583.
- Hirsсн А.: Ехtепsion оf thе 'Villarceau-Sektion' tо Surfaces of Revolution with а Generating Соniс. Jurnal for Сеоmetrу and Graphics, 6(2000/2). р. 121-132.
- Гирш А.Г. Обобщение «сечений Вилларсо» на поверхности вращения с образующей коникой. // Электронный журнал по прикладной геометрии. 2003. http://www.mai.ru/~apg/ Volume 5_n11. htm
- Гирш А. Г. Поверхность от вращения окружности. // Геометрия и графика. 2017, Т.5, №1. С. 32-35. ISIN: 2308 -4898.
- Stachel H.: Remarks on A.Hirsch's Paper conserning Villatceau-Sections. J. Geometry Graphics 6, p.133-139 (2002).
- http://www.anhirsch.de Антон Георгиевич Гирш (Dr. A.Hirsch) – Сайт.
Рисунки к докладу
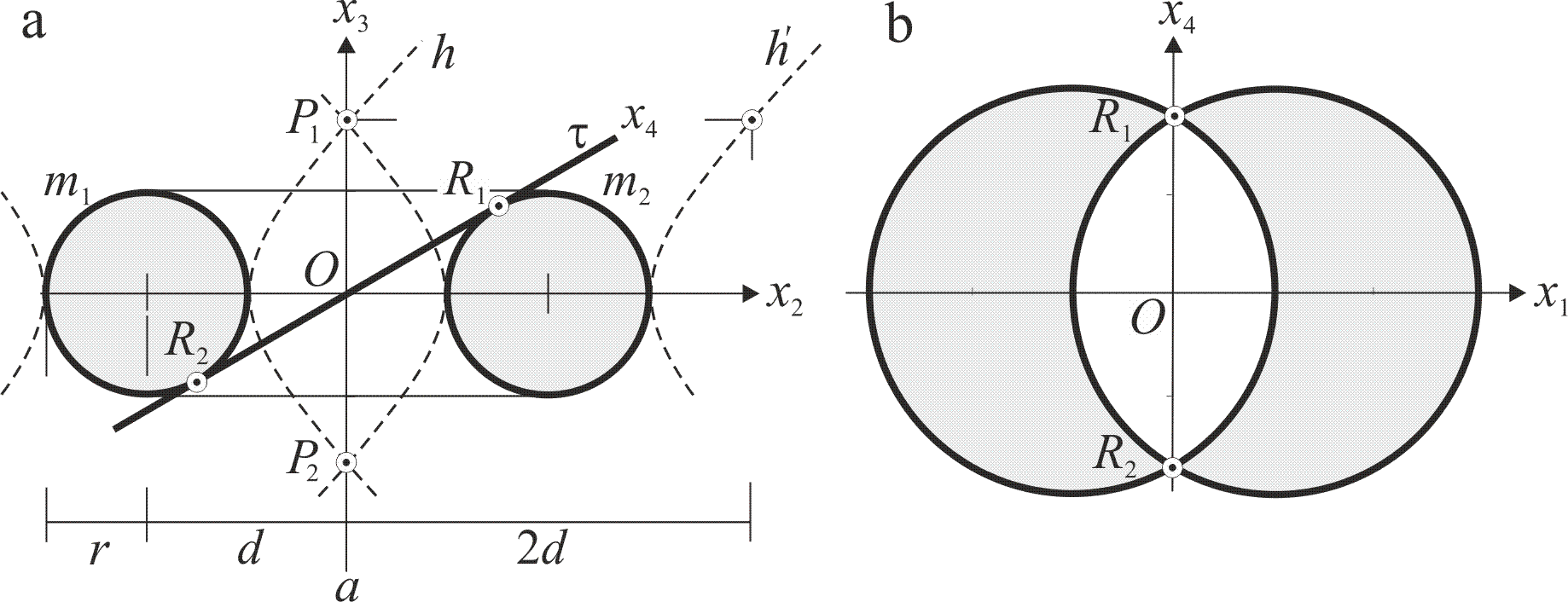
Рис. 1 а. Мнимые точки пересечения двух конгруэнтных окружностей. b. Распадение кривой τ-сечения, содержащей четыре двойные точки.
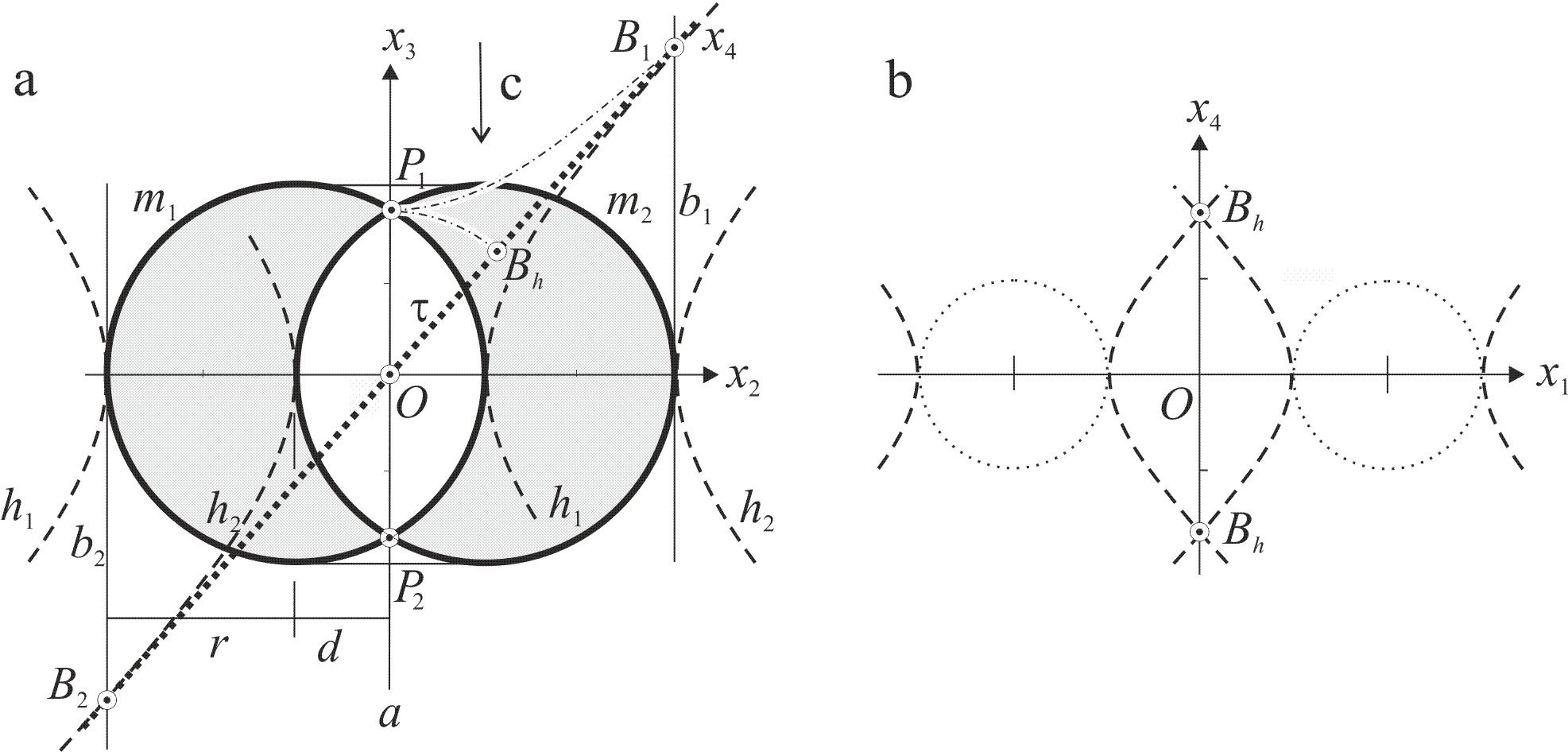
Рис. 2 Распадение сечения закрытого тора. а. Меридиан тора. b. Мнимые круги Вилларсо. с. Гиперболический поворот
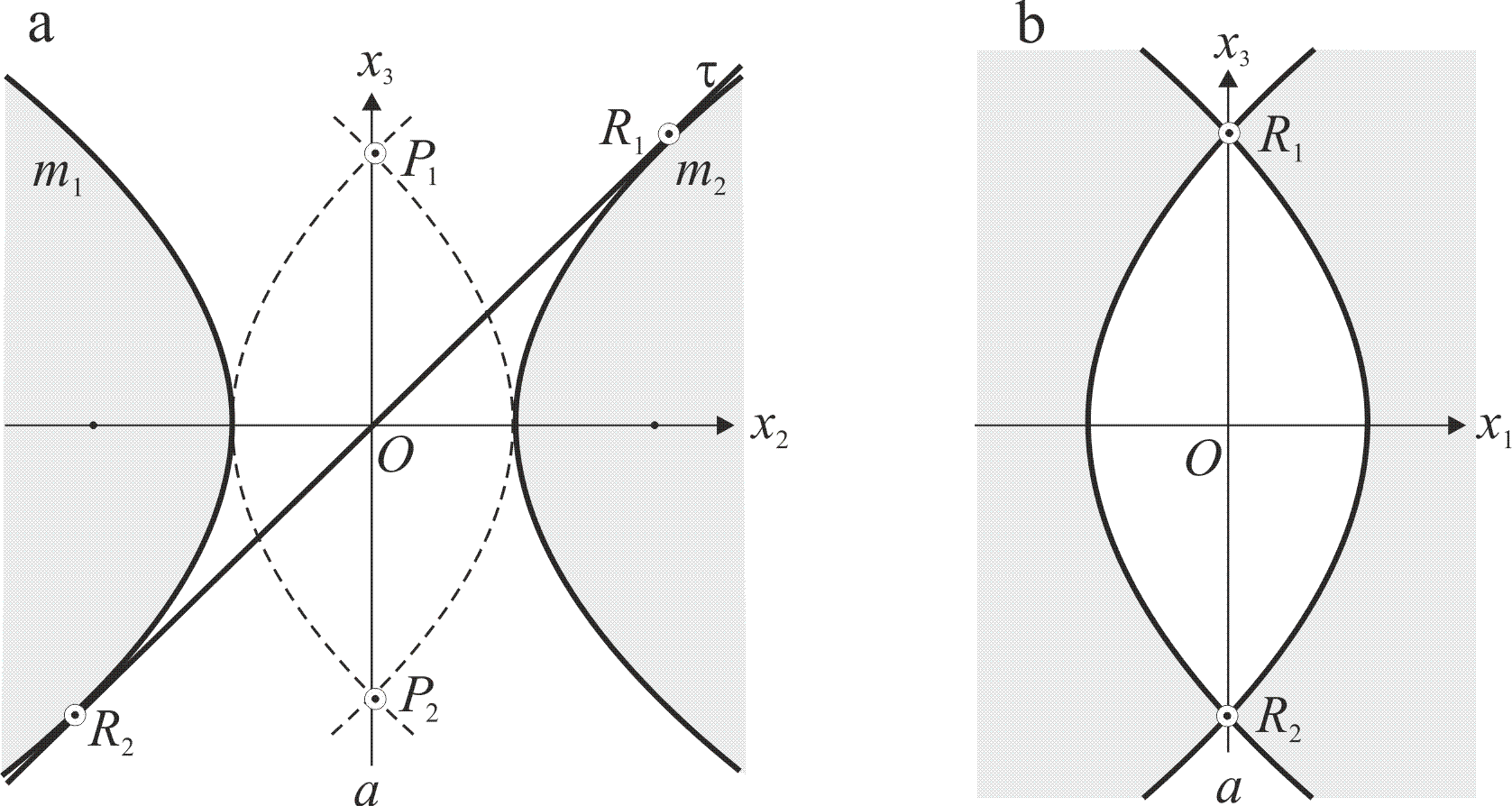
Рис. 3 Распадение сечения параболического тора. а. Меридиан тора m1, m2 и дважды касательная плоскость τ. b. Проекция сечения поверхности плоскостью τ
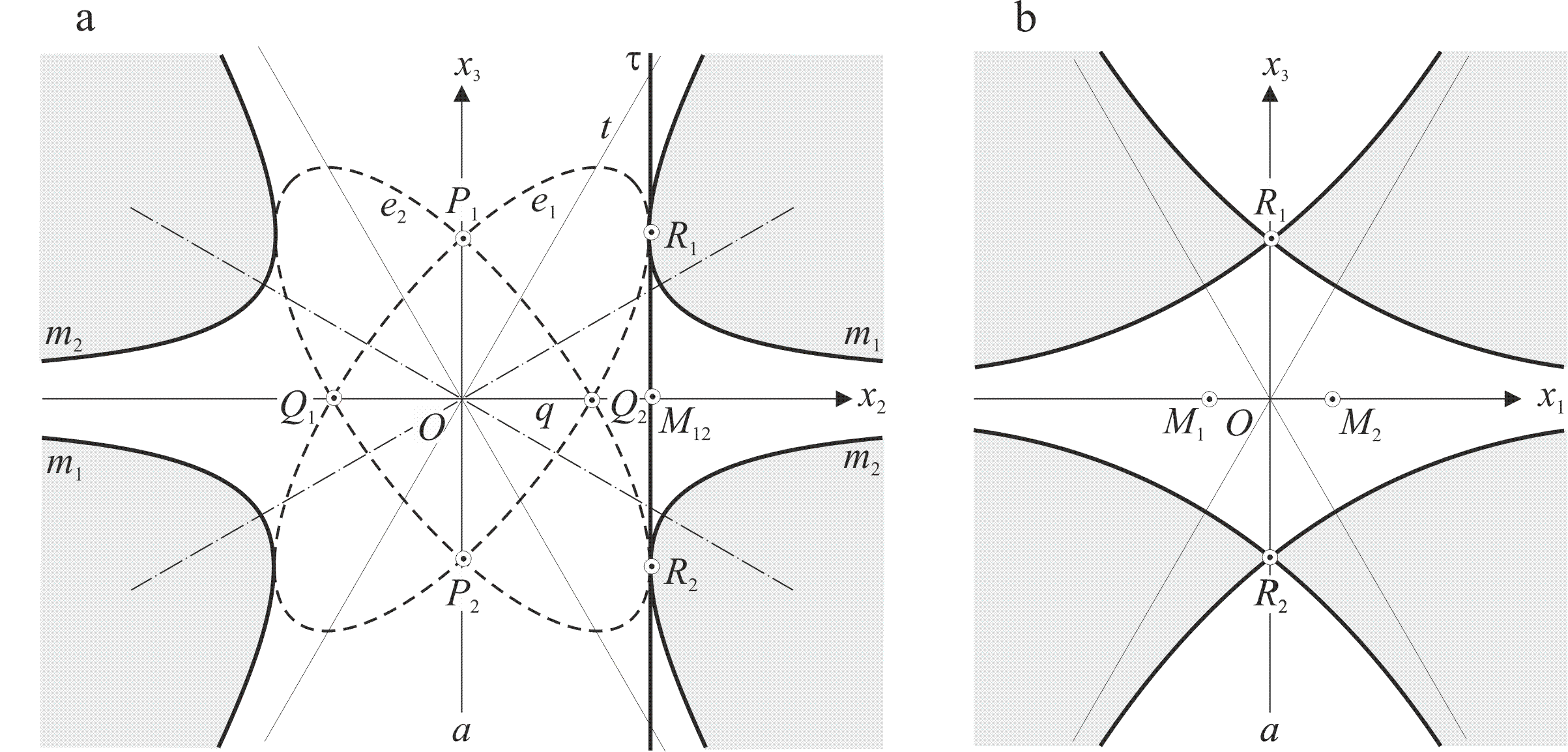
Рис. 4 Поверхность «шляпы». а. Меридиан m1, m2 поверхности и касательная плоскость τ. b. Сечение поверхности плоскостью τ
Вопросы и комментарии к выступлению:

Гирш Антон Георгиевич (5 марта 2019 г. 12:57) |
Ассоциация по примеру 1 связана с каплей. Каждая капля падая на поверхность воды выбивает в на ней кольцевую волну в виде валика, подскакивает и на мгновение зависает над водой в виде шарика. Поэты сравнивают это с серебряным гвоздиком. Такая картинка уже гуляет по интернету. Мне она напоминает открытый тор с изолированной точкой над ним. Математические поиски показали, что над поверхностью действительно находится изолированная точка, как сказал бы Ф.М. Суворов, воображаемая. |

Селиверстов Александр Владиславович (5 марта 2019 г. 14:29) |
Здравствуйте, Антон Георигевич! |

Гирш Антон Георгиевич (5 марта 2019 г. 15:51) |
Спасибо, Александр Владиславович. |

Бойков Алексей Александрович (26 марта 2019 г. 13:10) |
Здравствуйте, Антон Георгиевич! Большое спасибо за еще один интересный и глубоко геометрический доклад. Любопытно, что построить меридианы и задать секущую плоскость, которая дает, к примеру, мнимые круги Вилларсо, значительно проще, если пользоваться чертежом, чем в любой трехмерной САПР. с уважением, А.Бойков |
Назад Go Back