ОРТОГОНАЛЬНЫЕ МОНОПРОЕКЦИИ ШАРА, УСЕЧЕННОГО ПЛОСКОСТЯМИ ПРОИЗВОЛЬНОГО ПОЛОЖЕНИЯ
English version

|
Горнов Александр Олегович | (Национальный исследовательский университет "МЭИ") |
Аннотация
Рассматривается универсальный прием построения окружностей произвольного положения на шаре.
Ключевые слова: окружность, шар, нормаль, эллипс.
Широкая доступность средств КГ уже давно изменила прикладное значение тех или иных закономерностей и приемов построения и преобразования проекционных изображений в рамках технической графики, являющихся предметом НГ. Потребность в них сохранилось в рамках проектной графики для корректного построения “ручных” изображений эскизов и набросков, при оперативном графическом диалоге, исключения грубых ошибок при работе в САD. Кроме того, знания закономерностей проекционных процедур и изображений увеличивает "разрешающую способность" наблюдателя при оперативном анализе геометрической ситуации в окружающей обстановке. В частности тени, как проекционные фигуры, расширяют представление о предметной ситуации за счет дополнения информации об объектах и их элементах, в том числе не находящихся в прямой видимости. Думаю бесконечный спор о судьбе проекционных методов неконструктивен. Если в них совсем и нигде не будет потребности, то и говорить будет не о чем. Да и заставить применять проекционные процедуры там, где они нерациональны, вряд ли можно. И, попутно, относительно геометрии и начертательной геометрии. На мой взгляд последняя не является специфической геометрией, а есть один из методов отображения и преобразования геометрических характеристик объектов; тоже можно сказать, и уже говорилось [6], об аналитической геометрии.
В прошлом веке методы построения проекционных изображений, в частности аксонометрических и решения в их рамках ряда геометрических задач, имело самостоятельное значение для наглядной визуализации ТО. Поэтому этой проблеме была посвящена великолепная комплексная работа [1]. Что касается аналогии поставленной в статье задаче, в [1] в основном шла речь об изометрических проекциях окружностей как сечений шара, принадлежащих или параллельных основным плоскостям проекций; тоже можно найти и в известных учебниках [2,3] Помимо типовых приемов решения данной проекционно-графической задачи, но в расширенной постановке, описаны и другие [4,5].
Сформулируем далее подобную задачу еще несколько шире: о построении "аксонометрических" изображений окружностей, принадлежащих шару радиуса R0, как линий его сечения плоскостями произвольной ориентации.
Сначала кратко изложим предложенное в [4], на которое будем опираться в дальнейшем. Пусть хyz ортогональная тройка осей, в плоскости хy которой лежит окружность. Тогда ось z определяет нормаль Nz к этой плоскости, которая, наряду с началом координат, задает её положение при данном показателе искажения её проекции.
Ось x всегда можно совместить с диаметром окружности Dx=2R0 параллельным плоскости проекций, при этом показатель линейного искажения диаметра Dх будет равен единице (рис.1а.) Он проектируется без искажения, определяя величину и положение большой оси эллипса (а) и его проекция всегда перпендикулярна проекции нормали NZ к плоскости окружности и наоборот. Известное свойство суммы квадратов показателей искажения при ортогональном проецировании zyz: ∑J2xyz =2 позволяет определить показатель искажения диаметра DУ, перпендикулярного DХ, проекция которого есть малая ось эллипса b. При этом направление проекции нормали и проекция малой оси совпадают . Показатель искажения Jy определяет своей проекцией величину малой оси эллипса – проеции окружности DJy. Jy=√ 1-J2N. Эксцентриситет эллипса Е проекции окружности будет равен Е=DхJN. Вычисление Jу удобно графически с помощью прямоугольного треугольника. Этот же показатель искажения определяет проекции хорд h, параллельных данному диаметру, что позволяет построить проекции необходимого количества точек проекции окружности. А хорды, параллельные диаметру Dx, проектируются в натуральную величину.
Приложим эти соотношения к поставленной в начале задаче построения проекций окружностей как сечений шара плоскостями свободного положения. Пусть множество этих секущих плоскостей, в которых они лежат, определяют нормали, по модулю равные R0, для простоты исходящие из центра шара, а их соответствующие проекции есть N’1,2, ( Рис.1b). Положение конкретной плоскости определяет еще одна точка на данной нормали, отстоящая от центра на расстояние sR0 0≤s≤1. Величины s1,2 определяют радиусы окружностей R12, лежащей в этой плоскости.
В плоскости очерка проекции шара рис.1в заданы два направления проекции нормалей N1,2 секущих плоскостей. При этом JN1=JN2=0.64 и s1=0.5, а s2=0.7, т.е. первая секущая плоскость ближе к параллельной ей меридиональной плоскости, вторая дальше и ближе к поверхности шара. Определив диаметр окружности сечения при данном D шара параметрах и строим большую ось эллипса – a . Затем вычисляем или строим величину Jy малой оси .
Следует обратить внимание на положения проекции характерных точек касания очерка сферы и проекции окружности сечения. Они определяют переход линии проекции усеченного шара от его исходного очерка к проекции очерка усеченного. Положение этой точки определяется из следующих соображений. Через эту точку проходит линия пересечения p секущей плоскости и плоскости очерка шара, определение которой понятно из рисунка …Видно , что вторая секущая плоскость ( рис.1в) пересекает плоскость очерка вне его. Соответственно эллипс сечения не касается очерка сферы.
Полученные соотношения позволяют расширить классические задачи сечения сферических поверхностей в системе 2D проекций, где они практикуются, построением ассоциированной аксонометрии. При этом заметим, что распространенные в учебной практике приведенные аксонометрии изначально нерациональны, ибо искажают зрительные пропорции между 2D cистемой изображений объекта и аксонометрическим. Пусть задана фронтальная проекция трижды усеченного шара рис. 2а. Обозначим нормали к секущим плоскостям N1,2,3 . Построим, например изометрии этих нормалей N’123 и определим показатели линейного искажения JN123. Далее построения соответствуют изложенным выше.
Этот прием позволяет проиллюстрировать и проинтегрировать закономерности ортогональной проекции прямоугольной проекции тройки ортогональных векторов и прямого угла, основных характеристик эллипса. ….. Иллюстрации выполнены вручную, избегая соблазна воспользоваться соответствующей опцией САD.
Список литературы
-
Глазунов Е.А. Аксонометрия / Е.А. Глазунов, Н.Ф. Четверухин. ГИТЛ, Москва, 1953. 293с.
-
Фролов С.А. Начертательная геометрия / Учебник для втузов . – Машиностроение , 1978. – 240с.
-
Климухин А.Г. Начертательная геометрия/ Учебник для вузов . М.: Стройиздат . 1973.- 368с.
-
Горнов А.О. Ортогональная проекция окружности, лежащей в плоскости общего положения / А.О. Горнов. – Труды международной научно- технической конференции, Москва, МЭИ .2004 г. с. 67-70.
-
Андреев-Твердов А.И. / Построение аксонометрических проекций окружностей / А.И. Андреев-Твердов, Хуснетдинов Т.Р. /Журнал Актуальные проблемы гуманитарных и естественных наук N 3 Март 2017 г. С. 41-45.
-
Горнов А.О., Лепаров М.Н. Системные противоречия и предпосылки инженерной геометрии в образовательном аспекте. http://dgng.pstu.ru/conf2017/papers/91/
Рисунки к докладу
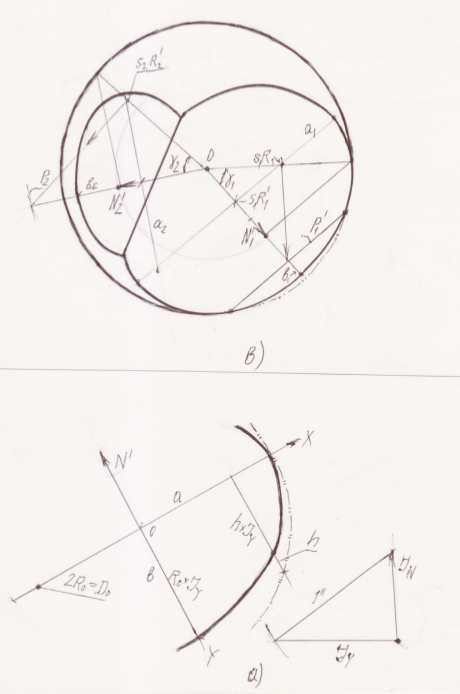
Рис. 1 К построению сечений шара: а) базовые построения; б) аксонометрия шара, произвольно усеченного двумя плоскостями
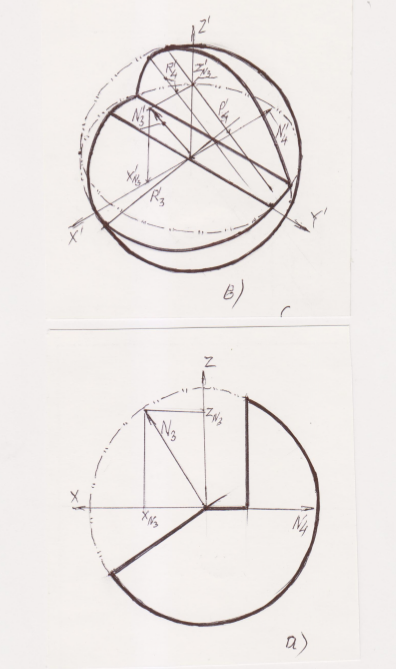
Рис. 2 Аксонометрия шара по исходной фронтальной проекции: а) исходная фронтальная проекция; б) ассоциативная аксонометрия при фактических показателях искажения
Вопросы и комментарии к выступлению:

Сальков Николай Андреевич (9 марта 2019 г. 19:32) |
Александр Олегович, ну что тут сказать, красивая работа. С уважением, Н. Сальков |

Горнов Александр Олегович (9 марта 2019 г. 21:20) |
Спасибо , Николай Андреевич.! Буду рад , если Вам пригодиться . А,О. |

Шацилло Людмила Анатольевна (9 марта 2019 г. 21:36) |
И заметьте, Николай Андреевич, от руки нарисовано! Такие вот специалисты! |

Сальков Николай Андреевич (9 марта 2019 г. 22:05) |
Людмила Анатольевна, я вижу!!! Мои студенты-архитекторы вместо эллипса рисуют бочковой огурец, хотя у них есть такой предмет как рисунок, и такой как живопись. Никак с ними не справиться, хотя, когда я при выдаче задания предупреждаю их об огурце - смеются, не верят, что у них тоже так получится. |

Хейфец Александр Львович (9 марта 2019 г. 22:37) |
Николай Андреевич, сформулируйте, пожалуйста, чем бочковой огурец в соответсвующей проекции и при идеализации его формы, по Вашему, отличается от эллипса. По научному, по каким критериям. Очень интересно. С уважением. А.Л. Хейфец. |

Полубинская Людмила Георгиевна (11 марта 2019 г. 16:14) |
Здравствуйте, уважаемый Александр Олегович!Спасибо и за статью, и за позицию в признании роли знания закономерностей проекционных процедур в процессе построения изображений.К сожалению, Вы сами знаете, сегодня геометрическая подготовка студентов такова, что объясняя тему со сферой приходится, и не единожды, «включать» пространственное мышление с помощью ассоциаций - глобус, земной шар с параллелями, меридианами и экватором; арбуз с положением ножа и формой куска. Однажды моя коллега на вопрос о форме куска арбуза получила ответ – треугольник! В таких ситуациях я каждый раз вспоминаю А.Л.Хейфеца – не нужно тратить время и силы на тех, кто не способен это понять! Предварительный отбор и отсев – вот, что изменит ситуацию с квалификацией выпускников нашей кафедры. Да и на квалификации преподавателей это скажется положительным образом! Но - «подушевое финансирование». Простите, ведь это совсем другая тема. (Начала почти с шутки, а кончила "за упокой")Об иллюстрациях - а почему не AutoCAD 2D? С неизменным уважением, Л.Г.Полубинская
|

Горнов Александр Олегович (11 марта 2019 г. 16:42) |
Здравствуйте Людмила Георгиевна! Честно, не думал, что маленькая статья о маленькой процедурной находке вызовет Ваш интерес. Надеюсь Вы не подумали (хотя дали основание так считать), что моя позиция о необходимости знания проекционных процедур результат постоянных дискуссий на эту тему. ( см. мои статьи хотя бы в рамках КГП ). В конце статьи указано ( см.) – рисунки намерено выполнены вручную, чтобы избежать соблазна использовать соответствующие опции САD . А это дизавуировало бы, на мой вгляд, написанное выше . С уважением, А.О. |
Назад Go Back