ПОСТРОЕНИЕ ГЛАВНЫХ ОСЕЙ КВАДРИКИ, ЗАДАННОЙ ДЕВЯТЬЮ ТОЧКАМИ

|
Короткий Виктор Анатольевич | (Южно-уральский государственный университет (Национальный Исследовательский Университет)) |
Аннотация
Задача построения квадрики по девяти точкам, в силу своей фундаментальной значимости, многократно рассматривалась математиками 19 века. Поиск простой геометрической зависимости, связывающей десять точек квадрики (аналогично теореме Паскаля, связывающей шесть точек конического сечения), не увенчался успе-хом. Тем не менее, были найдены различные алгоритмы геометрически точного (линейкой и циркулем или даже одной линейкой) построения любого количества точек квадрики, проходящей через девять данных точек. Практическая реализация алгоритмов, вследствие их большой сложности, возможна только с помощью средств компьютерной графики. В статье рассматривается один из известных алгоритмов, дополненный алгоритмом построения главных осей поверхности второго порядка, заданной девятью точками.
Ключевые слова: биквадратная кривая, пучок квадрик, пучок конических сечений, пространственная конфигурация Дезарга, геометрически точное построение, компьютерная графика.
1. Введение
“Несмотря на важность успехов, достигнутых в теории поверхностей второго порядка, надо заметить, что эти успехи составляют весьма малую долю тех, к которым, по-видимому, способна эта теория” [1]. Эти слова французского математика М. Шаля M. CHASLES (1793-1880), сказанные им в 1830 году, актуальны и сегодня. Например, в теории поверхностей второго порядка (квадрик) сохраняется принципиально важная “проблема десятой точки”. Речь идет о некоторой, пока не найденной, графической зависимости, которая, возможно, связывает десять точек квадрики (аналогично теореме Б. Паскаля B. PASCAL, связывающей шесть точек конического сечения).
Если такая зависимость для квадрик существует, то она может рассматриваться как своего рода “проективный эквивалент” алгебраического уравнения поверхности второго порядка. Попытки найти общее соотношение между десятью произвольными точками квадрики, предпринятые немецкими и французскими математиками в 19 столетии, не привели к какому-либо существенному успеху. В более позднее время интерес к этой проблеме полностью пропал.
Но усилия не были напрасны. Были найдены различные варианты графического решения задачи построения квадрики, проходящей через девять данных точек [9, 10]. К сожалению, алгоритмы оказались очень сложны (особенно по сравнению со схемой Б. Паскаля B. PASCAL, позволяющей решить аналогичную задачу для конических сечений), и практически неприменимы.
В конце 20 века ситуация принципиально не изменилась, но появилась компьютерная графика. Средства компьютерной графики позволяют практически выполнять любые, как угодно сложные, графические построения. В частности, кривые второго порядка стали такими же простыми и точно вычерчиваемыми линиями, как прямая и окружность [4, 5]. Возможно, новые инструментальные средства возродят интерес к теории поверхностей второго порядка.
2. Постановка задачи
В трехмерном евклидовом пространстве указаны точки 1,2,…,9. Девять точек общего положения определяют единственную квадрику Θ, проходящую через эти точки. Данные точки не должны располагаться на одной биквадратной кривой, поскольку указание любого числа точек на такой кривой не определяет однозначно поверхность второго порядка. Три данные точки не должны принадлежать одной прямой, поскольку в этом случае вся прямая и все точки на ней принадлежат искомой поверхности. Шесть данных точек не должны принадлежать одной кривой второго порядка, поскольку все точки на этой кривой принадлежат искомой поверхности.
Через одну из точек 1,2,…,9 проведем прямую общего положения t. “Проблема десятой точки” формулируется следующим образом: с помощью линейки построить вторую точку пересечения прямой t с квадрикой Θ (найти десятую точку квадрики).
Задача может быть сформулирована менее строго: найти графический алгоритм построения множества точек квадрики, заданной девятью точками.
Поставленная задача дополняется требованием построения главных диаметров искомой квадрики Θ. Алгебраическое решение дополнительной задачи сводится к решению характеристического уравнения третьего порядка. Эквивалентное геометрическое решение сводится к построению трех точек пересечения двух конических сечений, одна общая точка которых известна. Это задача третьей степени, которая не может быть решена циркулем и линейкой.
Следует отметить, что задача построения квадрики по девяти точкам, в силу своей фундаментальной значимости, многократно рассматривалась математиками 19 века. Краткий обзор решений дан в статье [10]. Рассмотрим алгоритм ROHN-PAPPERITZ (1896) [9]. Этот алгоритм наиболее нагляден и наилучшим образом пригоден для его конструктивной реализации средствами компьютерной графики. Другие алгоритмы заметно сложнее [7].
3. Алгоритм ROHN-PAPPERITZ
В трехмерном пространстве указаны девять точек общего положения 1, 2,…, 9. Требуется построить поверхность второго порядка Θ, проходящую через данные точки.
Отмечаем плоскости α(123), β(456), γ(789). Прямые линии m=α∩β, n=β∩γ, l=α∩γ пересекаются в точке P. Согласно [9], решение сводится к построению конических сечений a2(1, 2, 3), b2(4, 5, 6), g2(7, 8, 9), попарно пересекающихся на прямых m, n, l. Эти конические сечения вполне определяют искомую поверхность Θ (рис. 1).
Совместно рассмотрим плоскости α и β. На прямой m=α∩β укажем произвольные точки M, N. Через точки 1, 2, 3, M, N в плоскости α проведем коническое сечение a2. Через точки 4, 5, 6, M, N в плоскости β проведем коническое сечение b2 (рис. 2).
Определение. Конические сечения a2, b2, лежащие в плоскостях α и β, назовем “сопряженными”, если они пересекаются в точках, лежащих на прямой m=α∩β.
Начертим поляры pa, pb точки P относительно конических сечений a2, b2. Поляры сопряженных конических сечений также назовем “сопряженными”. Сопряженные поляры пересекаются в точках, лежащих на прямой m. Множеству сопряженных конических сечений a2~b2 соответствует множество сопряженных поляр pa~pb.
Произвольно указывая точки M, N на прямой m, начертим в плоскостях α, β три пары сопряженных конических сечений a2~b2, a′2~b′2, a′′2~b′′2. Трем парам сопряженных конических сечений соответствуют три пары сопряженных поляр pa~pb, p′a~p′b, p′′a~p′′b. Сопряженные поляры попарно пересекаются на прямой m, образуя пространственную конфигурацию Дезарга DESARGUES с центром Oαβ и осью m. Центр Oαβ находится на пересечении прямых, соединяющих соответственные точки (pa∩p′a)↔(pb∩p′b), (p′a∩p′′a)↔(p′b∩p′′b), (pa∩p′′a)↔(pb∩p′′b).
Аналогично устанавливаются перспективные соответствия между парами плоскостей α↔γ (с центром Oαγ и осью l=α∩γ) и β↔γ (с центром Oβγ и осью n=β∩γ).
Отметим важный результат. Пусть через один из центров, например, через центр Oαβ, проведена произвольная плоскость δ. Плоскость δ пересекается с плоскостями α, β по прямым pα=δ∩α, pβ=δ∩β. Эти прямые могут считаться сопряженными полярами (относительно полюса P) двух сопряженных конических сечений dα2(1, 2, 3)~dβ2(4, 5, 6). Коническое сечение dα2, проходящее через точки 1, 2, 3, вполне определено полюсом P и полярой pα. Коническое сечение dβ2, проходящее через точки 4, 5, 6, вполне определено полюсом P и полярой pβ.
Таким образом, произвольная плоскость δ, инцидентная центру Oαβ, порождает в плоскостях α, β пару сопряженных конических сечений, проходящих через данные точки (1, 2, 3) и (4, 5, 6). Следовательно, плоскость Δ(OαβOαγOβγ) порождает в плоскостях α, β, γ три пары сопряженных конических сечений a2~b2, a2~g2, b2~g2, проходящих через данные точки (1, 2, 3), (4, 5, 6), (7, 8, 9). Эти конические сечения определяют искомую поверхность Θ. Задача решена.
4. Построение главных осей и плоскостей симметрии
Квадрика Θ задана девятью точками общего положения. Требуется построить главные оси квадрики.
Используя рассмотренный выше алгоритм, находим какое-либо коническое сечение θ2 квадрики Θ. Наличие непрерывно начерченной коники θ2 позволяет выполнять вспомогательные построения, необходимые для построения главных осей квадрики.
Находим центр O квадрики и выделяем связку прямых и плоскостей O(d, Σ), сопряженных относительно Θ. В этой связке произвольному диаметру d соответствует сопряженная диаметральная плоскость Σ (плоскость Σ проходит через середины хорд, параллельных диаметру d). В связке O(d, Σ) имеются три пары взаимно перпендикулярных диаметров d и три пары взаимно перпендикулярных диаметральных плоскостей Σ. Это и есть искомые главные оси и плоскости симметрии квадрики Θ.
Рассмотрим ортогональное соответствие в связке O: каждой плоскости Σ соответствует перпендикуляр n, проходящий через точку O. Между двухпараметрическим множеством прямых линий d и n в связке O установлено проективное соответствие ΛO. Три пары совпавших прямых d≡n указывают три главных диаметра квадрики Θ.
Начертим четыре пары прямых d1~n1, d2~n2, d3~n3, d4~n4, соответственных в ΛO. Проводим произвольную секущую плоскость Π. Плоскость Π пересекает соответственные прямые в соответственных точках D1~N1, D2~N2, D3~N3, D4~N4. Получаем совмещенные точечные поля Π=ΠD=ΠN. Четыре пары точек определяют коллинеацию Δ(ΠD↔ΠN). Требуется найти три двойные точки этой коллинеации.
Согласно [3], для построения двойных точек коллинеации Δ отметим в плоскости ΠD произвольную точку D0. Начертим пучок прямых D0(D0D1, D0D2, D0D3, D0D4). В плоскости ΠN найдем точку N0, соответствующую точке D0 в коллинеации Δ. Начертим пучок прямых N0(N0N1, N0N2, N0N3, N0N4). Пучки D0 и N0 проективны. Точки пересечения соответственных лучей этих пучков образуют некоторое коническое сечение h2.
Будем полагать, что кривая h2 относится к полю ΠD. В поле ΠN найдем конику h2N, соответствующую конике h2 в коллинеации Δ. Кривые h2 и h2N пересекаются в точке N0 и в трех двойных точках X, Y, Z коллинеации Δ(ΠD↔ΠN). Построение точек (X, Y, Z)=h2∩h2N не может быть выполнено циркулем и линейкой, поскольку это задача третьей степени. Для ее конструктивного решения используется компьютерная программа [5]. Главные оси квадрики Θ проходят через центр O и через точки X, Y, Z. Плоскости симметрии перпендикулярны главным осям. Задача решена.
5. Заключение
Развитие компьютерной графики в конце 20 века привело к появлению своеобразного “проективно-вычислительного” метода геометрического моделирования, объединяющего преимущества синтетических и аналитических методов исследования. Новый метод сочетает в себе высокую точность компьютера, любые действия которого в принципе основаны на координатных расчетах, и геометрическую простоту проективных алгоритмов, в которых имеют значение лишь инциденции точек и прямых. В этом сочетании можно усмотреть окончательное завершение “идеологического противостояния” аналитической геометрии (Р. Декарт R. DESCARTES, 1596-1650) и проективной геометрии (Ж. Дезарг G. DESARGUES, 1591-1661).
Современные средства компьютерной графики позволяют конструктивно реализовать сложные графические алгоритмы, в том числе проективные алгоритмы построения квадрики, заданной девятью точками. Алгебраическое решение этой задачи заключается в вычислении коэффициентов общего уравнения искомой квадрики, исходя из системы девяти линейных уравнений относительно девяти неизвестных коэффициентов. Эквивалентное геометрическое решение также должно быть линейным, то есть должно выполняться с помощью одной линейки и даже без применения циркуля. Этому требованию удовлетворяет алгоритм ROHN-PAPPERITZ [9], хотя, конечно, рассмотренная в статье компьютерная реализация этого алгоритма, предполагающая использование программы “Компьютерный коникограф”, выводит нас за рамки геометрически точного решения. Программа выполняет геометрически точное (“циркулем и линейкой”) построение метрики кривой второго порядка, заданной набором пяти линейных инциденций (точек и касательных) [4]. Точки и касательные могут быть как вещественными, так и мнимыми [2, 6]. После определения метрики программа вычерчивает непрерывную кривую второго порядка, удовлетворяющую заданным условиям инцидентности. Применение подобной программы никак не способствует решению теоретической “проблемы десятой точки”, но позволяет составить сравнительно простой компьютерный алгоритм построения квадрики, альтернативный алгебраическому решению. Для проверки точности алгоритма был выполнен математический эксперимент: составлен электронный макет эллипсоида и отмечены девять произвольно выбранных точек на его поверхности. Затем эллипсоид вместе с главными осями “заморожен”. В соответствии с алгоритмом ROHN-PAPPERITZ, дополненным блоком построения главных осей, были “экспериментально определены” вершины эллипсоида (концы главных осей). После размораживания эллипсоида оказалось, что вершины электронного макета эллипсоида совпадают с “экспериментально найденными” вершинами с точностью до объектных привязок. Иными словами, компьютер не сумел зафиксировать отличие координат вершин заданного эллипсоида от координат вершин, найденных посредством проверяемого алгоритма. Следовательно, точность алгоритма не ниже точности используемой в эксперименте графической программы (AutoCAD).
Список литературы
- M. CHASLES: Aperçu historique sur l'origine et le développement des methods en Géométrie particuliérement de celles qui se rapportent à la Géométrie moderne. Paris 1875.
- A. GIRSH, V. KOROTKIY: Graphic Reconstruction Algorithms of the Second-Order Curve, given by the Imaginary Elements. Journal of Geometry and Graphics 4, 19-30, Moscow 2016.
- N.A. GLAGOLEV: Projective Geometry. Moscow 1963.
- V. KOROTKIY: Synthetic Algorithms of Construction of the Curve of the Second Order. Journal of Computer & Information Technology 11 (125), 20-24, Moscow 2014.
- V. KOROTKIY, L. KHMAROVA: Universal computer program for drawing conic sections. GraphiCon 2016, 347-351, Russia, Nizhnij Novgorod 2016.
- V. KOROTKIY: Computer visualization of the second order curve passing through imaginary points and touching imaginary straight lines. Scientific Visualization, Russia, Volume 10 (2018), No. 1, 56-68.
- V. KOROTKIY: Construction of a Nine-Point Quadric Surface. Journal for Geometry and Graphics, Austria, Volume 22 (2018), No. 2, 183-193.
- T. REYE: Die Geometrie der Lage. II. Theil. Leipzig, Baumgärtner′s Buchhandlung 1892.
- K. ROHN, E. PAPPERITZ: Lehrbuch der Darstellenden Geometrie. Band II, Leipzig 1896.
- O. STAUDE: Flaechen 2. Ordnung und ihre Systeme und Durchdringungskurven. In Encyklopaedie der Mathematischen Wissenschaften, Band III, Geometrie, Teil 2, Hälfte 1, Teubner, Leipzig 1903.
Рисунки к докладу
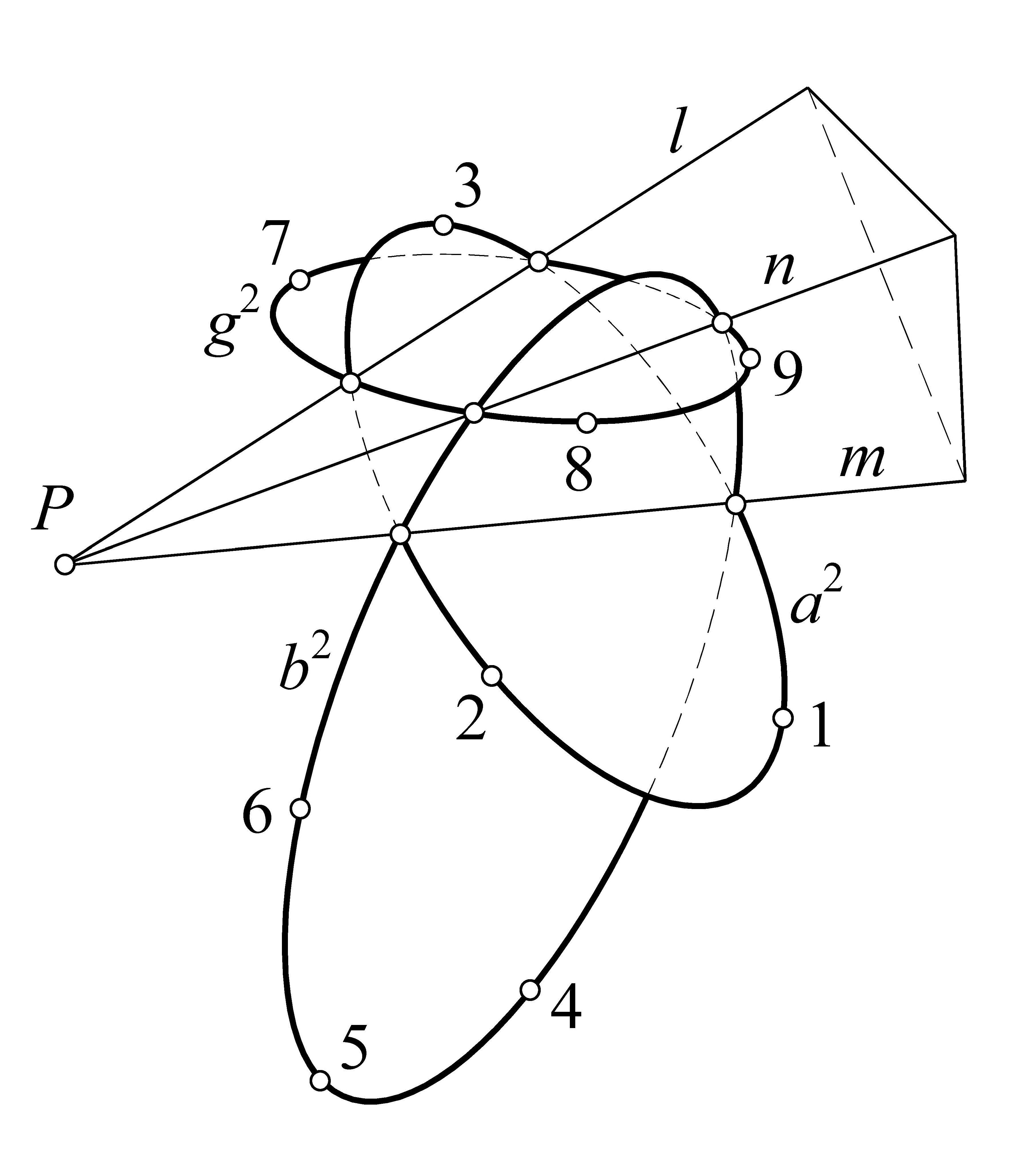
Рис. 1 Коники a2, b2, g2 определяют квадрику
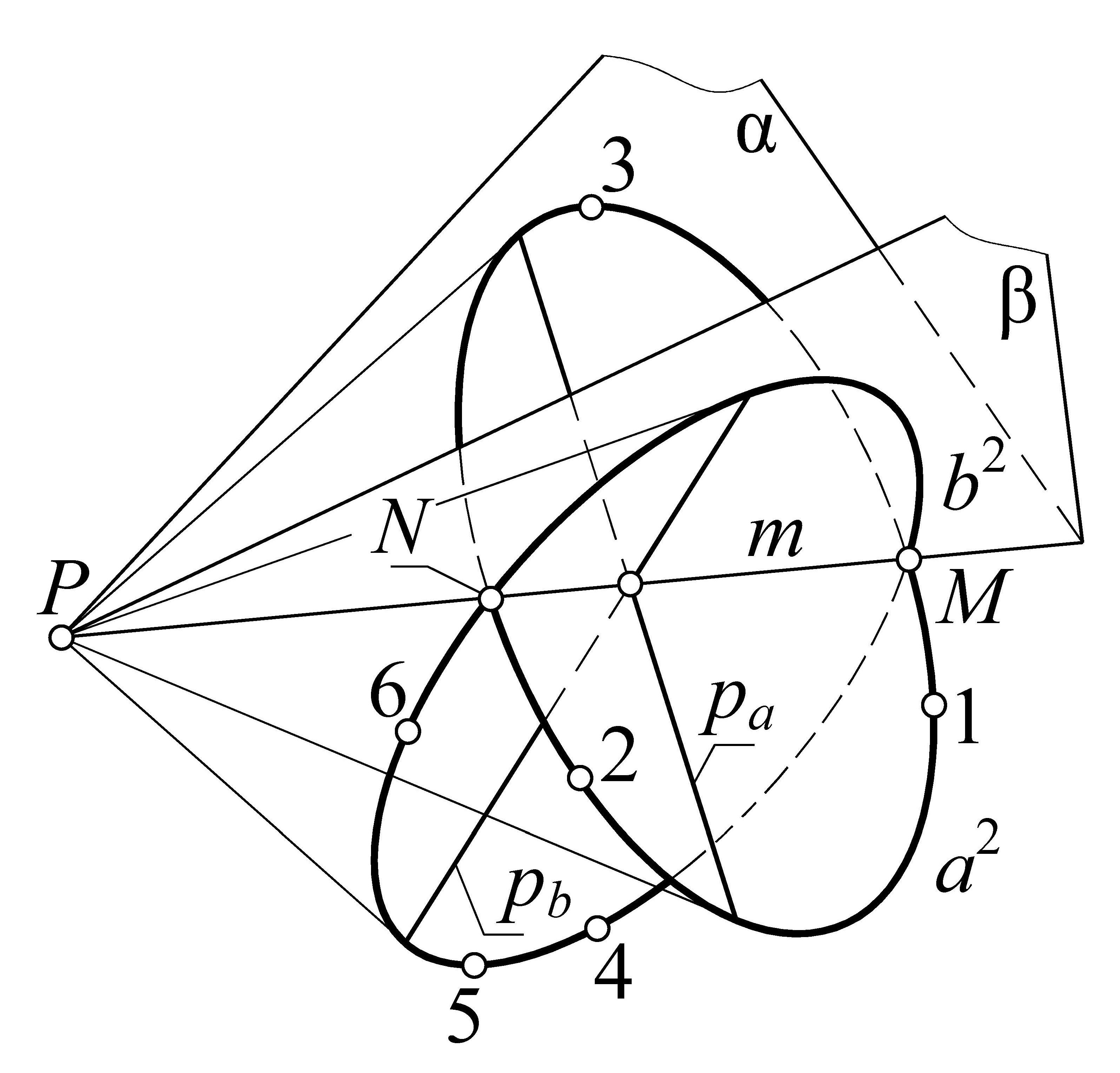
Рис. 2 Сопряженные коники a2~b2
Вопросы и комментарии к выступлению:

Селиверстов Александр Владиславович (10 марта 2019 г. 20:12) |
Здравствуйте, Виктор Анатольевич. |

Волошинов Денис Вячеславович (12 марта 2019 г. 23:18) |
Виктор Анатольевич, спасибо за алгоритм! Проверил, все работает, как часы! |

Гирш Антон Георгиевич (14 марта 2019 г. 1:17) |
Александр Владиславович, да что это Вы так переоцениваете циркуль и линейку. Анахронизм какой-то. Уверен, что не у каждого студента есть тот циркуль. А этот пример с девятью точками поверхности второго порядка как раз и подтверждает пользу 3Д компьютерной графики и видимо в пользу сторонников последней. По поводу сферы, по точкам которой воссоздавалась бы поверхность, Вы хорошо подметили, сам такое практикую в частности окружность как коника. |

Хейфец Александр Львович (14 марта 2019 г. 7:25) |
Антон Георгиевич, вот и Вы стали признавать роль 3d в геометрическом моделировании, а ведь сравнительно недавно резко отзывались об этом направлении, да и обо мне в связи с этим. Время работает... У меня несколько вопросов к Вам по статье о квадриках по 9-ти точкам. По моему, это Ваша заслуга в том, что подняли эту задачу из истории. Но в своей статье в ГиГ и выступлении на КГП Вы говорили о том, что общее решение задачи не найдено и приводили лишь частный случай ее решения. Здесь же я вижу в статье победные фразы "Задача решена". Так, по Вашему мнению, решена задача? Мне, с моим "средневековым" инженерным мышлением трудно разобраться в приведенном алгоритме, но задача очень интересует. Поэтому, важны комментарии по задаче. Алгоритм - это "делай раз, делай два ... и готово". "Готово" - это программа построения квадрики по предварительно заданным точкам. Есть здесь такой алгоритм? Я его не увидел. Если построены главные оси квадрики, то этого ведь недостаточно. Это могут быть оси и эллипсоида, и параблоида, и гиперболоида. Так решена задача? С уважением. А.Л. Хейфец. |

Гирш Антон Георгиевич (14 марта 2019 г. 10:15) |
1) Александр Владиславович, для сферы не стоит задача нахождения трёх главных осей! 2) Александр Львович, да, когда писал в ГиГ, то не провёл основательного литературного поиска. Подсказку получил от Виктора Анатольевича, а потом, да потом, посыпалось. Похоже было, что каждый, считавший себя геометром в 19 в. приложился к этой задаче. Решений много и разнообразных, не все приемлемы на сегодня. Решил ли В.А. Короткий задачу построения ПВП по её девяти точкам? Да, решил. Современным методом. 3) Не хочу быть участником полемики "что было первично - яйцо или курица?". Машинная графика нужна, но и геометрию никто не отменял. Компьютер - инструмент, помощник, а решение задачи происходит в голове, в которой должно быть пространственное геометрическое представление. Обе спорящие стороны правы, война о том "с какого конца начинать чистить яйцо". 4) Виктор Анатольевич, Вы предложили корректное и исчерпывающее решение классической фундаментальной задачи прикладной геометрии. Приятное достижение. С уважением. Антон Г. Гирш. |

Селиверстов Александр Владиславович (14 марта 2019 г. 13:20) |
Здравствуйте, Антон Георгиевич! |

Короткий Виктор Анатольевич (14 марта 2019 г. 14:55) |
Вынужден с сожалением признать, что не имею никакого отношения к представленному решению. Оно опубликовано в учебнике K. ROHN, E. PAPPERITZ: Lehrbuch der Darstellenden Geometrie. Band II, Leipzig 1896. С уважением, В. Короткий
|

Хейфец Александр Львович (14 марта 2019 г. 19:54) |
Антон Георгиевич, Вы поздравляете автора статьи о квадриках с тем, что он предложил "корректное и исчерпывающее решение классической фундаментальной задачи прикладной геометрии. Приятное достижение." А он в ответ пишет что не имеет никакого отношения к представленному решению и что оно "опубликовано в учебнике K. ROHN, E. PAPPERITZ: Lehrbuch der Darstellenden Geometrie. Band II, Leipzig 1896." И это при том, что Вы сами опубликовали ряд статей по этой задаче. Получается, что Вы не в теме задачи, по которой пишете статьи. А как по другим темам Ваших работ? С уважением. А.Л. Хейфец. |

Волошинов Денис Вячеславович (15 марта 2019 г. 1:52) |
Рис. 1. Исходные данные и частично промежуточные результаты .
Рис. 2. Первая пара коник в плоскости alpha.
Рис. 3. Вторая пара коник в плоскости alpha.
Рис. 4. Третья пара коник в плоскости alpha.
Рис. 5. Центр Oαβ . Рис. 6 - 13 не привожу. Их суть аналогична приведенным.
Рис. 14. Три коники результата. Толстая линия - фронтальная проекция, тонкая линия - горизонтальная проекция.
Рис. 15. Все построение целиком. |

Хейфец Александр Львович (15 марта 2019 г. 6:25) |
Денис Вячеславович, дайте комментарий к Вашим приведенным построениям. Это связано с построением квадрики, правильно? Так, где квадрика в итоге? Ни у Вас, ни у автора ее не видно. С уважением. А.Л. Хейфец. |

Волошинов Денис Вячеславович (15 марта 2019 г. 9:32) |
Определитель квадрики приведен на рис. 14. Если есть определитель и способ построения точки на задающей им поверхности, то с моделью поверхности можно решать любые задачи. Представленный алгоритм дает возможность это делать, а значит, в самое ближайшее время появятся множество функции, которых очень не хватало для использования квадрик в проективных преобразованиях и преобразованиях инверсии. Перевод модели в 3DsMax для визуализации приведу позже после публикации материала о связи Симплекса с этой системой. Сейчас такой перевод не предсталяет принципиальной проблемы (см,, например, "https://vk.com/geometry_descriptive"). Для решения позиционных и метрических задач визуализация квадрики не нужна. Алгоритм как раз и позволяет делать эту визуализацию без каких-либо ограничений универсально для любых квадрик, но дело даже не в этом. Самое главное - это то, что алгоритм позволил ясно понять, как строить гиперквадрики в пространствах с разменостью большей третьей. Вот это действительно прорыв! Аналогичный подход применительно к решению задачи Аполлония в четырехмерном пространстве представлен, например, в статье https://tuzs.sut.ru/release/tuzs_v4_i2_y2018/article_5.pdf.
|

Волошинов Денис Вячеславович (15 марта 2019 г. 9:43) |
Александр Львович! Приношу извинение за то, что не поприветствовал Вас в предыдущем сообщении. |

Гирш Антон Георгиевич (17 марта 2019 г. 13:51) |
Уважаемый Александр Львович, Вы утверждаете, что нет пророка в своём отечестве! Для начала, слово "решил" имеет несколько смыслов, и как нашёл идею решения, и как исполнил построение. В последнем случае могут быть разные пути исполнения решения. Задача 9-и точек имеет с десяток разных решений. Ну и что, что В.А. Короткий говорит, что взял решение у K. Rohn и E. Papperitz. Что он у них мог взять? Скорее, идею решения, а исполнение провёл 1) по собственным алгоритмам, 2) с применением коникографа, 3) с использованием 3D-программы. То я и сказал: решил современным способом. Разве не приятно, что в наших рядах есть талантливые и трудолюбивые коллеги? Очень уж сурово Вы судите, Александр Львович. С уважением. Антон Г. Гирш. |

Хейфец Александр Львович (17 марта 2019 г. 14:32) |
Антон Георгиевич, извините за допущенную мною резкость. Просто, задача очень интересует, а вижу, что вокруг нее больше, скажу так: непонятных мне разговоров, которые закнчиваются фразами, что решение получено. А решения не видно. Так, разве можно считать решением нахождение главных осей. Ведь эти три отрезка дают всего лишь центр и могут соответсвовать любому типу квадрики. Да и на Вас я оглядывался, поскольку Вы в своих статьях говорили, что решения в общем случае не найдено. Похоже, придется самому взяться за понятное инженерному мышлению решение. С искренним уважением. А.Л. Хейфец.
|
Назад Go Back





